文档内容
2013年全国统一高考数学试卷(理科)(大纲版)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.(5分)设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M
中元素的个数为( )
A.3 B.4 C.5 D.6
【考点】13:集合的确定性、互异性、无序性;1A:集合中元素个数的最值.
菁优网版权所
有
【专题】11:计算题.
【分析】利用已知条件,直接求出a+b,利用集合元素互异求出M中元素的个数
即可.
【解答】解:因为集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},
所以a+b的值可能为:1+4=5、1+5=6、2+4=6、2+5=7、3+4=7、3+5=8,
所以M中元素只有:5,6,7,8.共4个.
故选:B.
【点评】本题考查集合中元素个数的最值,集合中元素的互异性的应用,考查
计算能力.
2.(5分) =( )
A.﹣8 B.8 C.﹣8i D.8i
【考点】A5:复数的运算.
菁优网版权所有
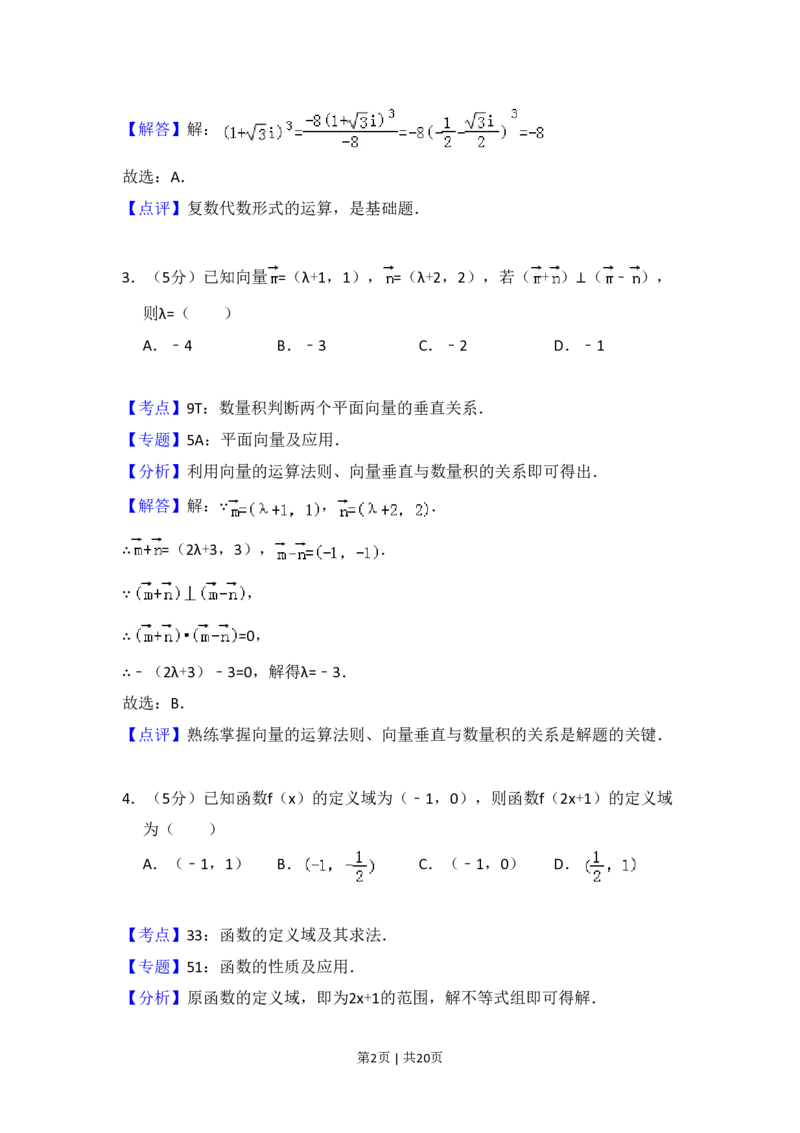
【分析】复数分子、分母同乘﹣8,利用1的立方虚根的性质(
),化简即可.
第1页 | 共20页【解答】解:
故选:A.
【点评】复数代数形式的运算,是基础题.
3.(5分)已知向量 =(λ+1,1), =(λ+2,2),若( + )⊥( ﹣ ),
则λ=( )
A.﹣4 B.﹣3 C.﹣2 D.﹣1
【考点】9T:数量积判断两个平面向量的垂直关系.
菁优网版权所有
【专题】5A:平面向量及应用.
【分析】利用向量的运算法则、向量垂直与数量积的关系即可得出.
【解答】解:∵ , .
∴ =(2λ+3,3), .
∵ ,
∴ =0,
∴﹣(2λ+3)﹣3=0,解得λ=﹣3.
故选:B.
【点评】熟练掌握向量的运算法则、向量垂直与数量积的关系是解题的关键.
4.(5分)已知函数f(x)的定义域为(﹣1,0),则函数f(2x+1)的定义域
为( )
A.(﹣1,1) B. C.(﹣1,0) D.
【考点】33:函数的定义域及其求法.
菁优网版权所有
【专题】51:函数的性质及应用.
【分析】原函数的定义域,即为2x+1的范围,解不等式组即可得解.
第2页 | 共20页【解答】解:∵原函数的定义域为(﹣1,0),
∴﹣1<2x+1<0,解得﹣1<x<﹣ .
∴则函数f(2x+1)的定义域为 .
故选:B.
【点评】考查复合函数的定义域的求法,注意变量范围的转化,属简单题.
5.(5分)函数f(x)=log (1+ )(x>0)的反函数f﹣1(x)=( )
2
A. B. C.2x﹣1(x∈R)
D.2x﹣1(x>0)
【考点】4R:反函数.
菁优网版权所有
【专题】51:函数的性质及应用.
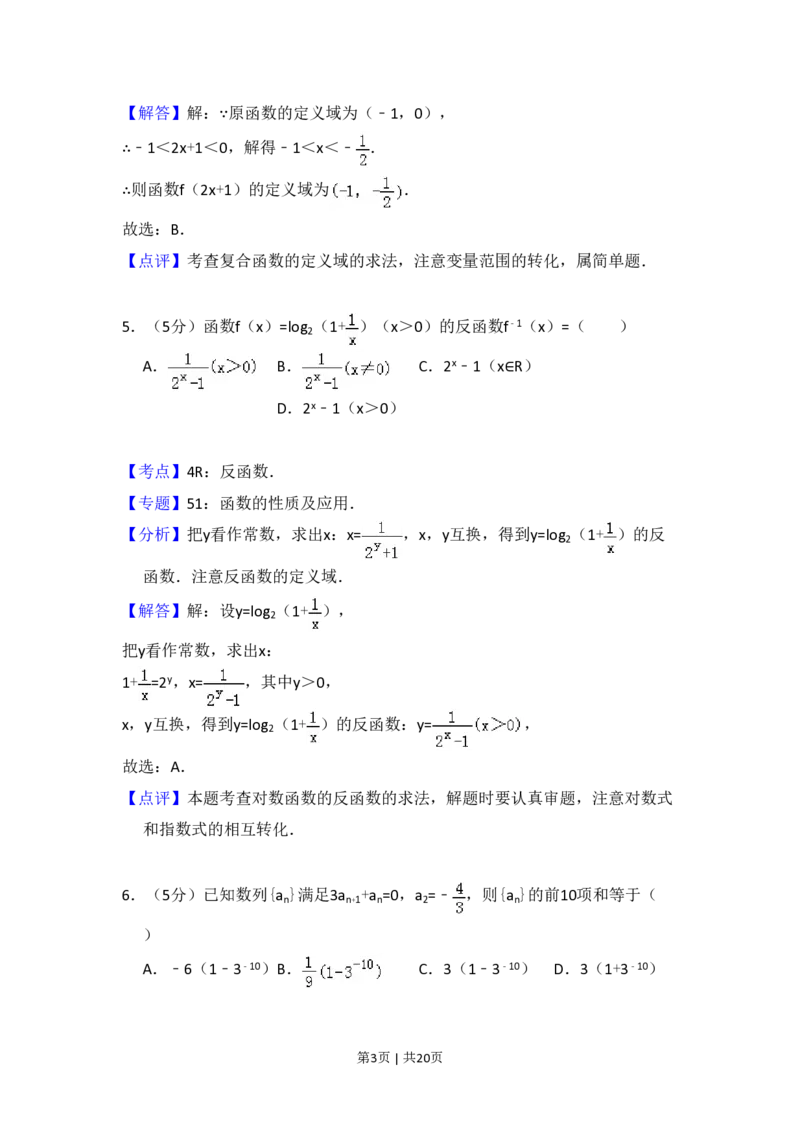
【分析】把y看作常数,求出x:x= ,x,y互换,得到y=log (1+ )的反
2
函数.注意反函数的定义域.
【解答】解:设y=log (1+ ),
2
把y看作常数,求出x:
1+ =2y,x= ,其中y>0,
x,y互换,得到y=log (1+ )的反函数:y= ,
2
故选:A.
【点评】本题考查对数函数的反函数的求法,解题时要认真审题,注意对数式
和指数式的相互转化.
6.(5分)已知数列{a }满足3a +a =0,a =﹣ ,则{a }的前10项和等于(
n n+1 n 2 n
)
A.﹣6(1﹣3﹣10)B. C.3(1﹣3﹣10) D.3(1+3﹣10)
第3页 | 共20页【考点】89:等比数列的前n项和.
菁优网版权所有
【专题】11:计算题;54:等差数列与等比数列.
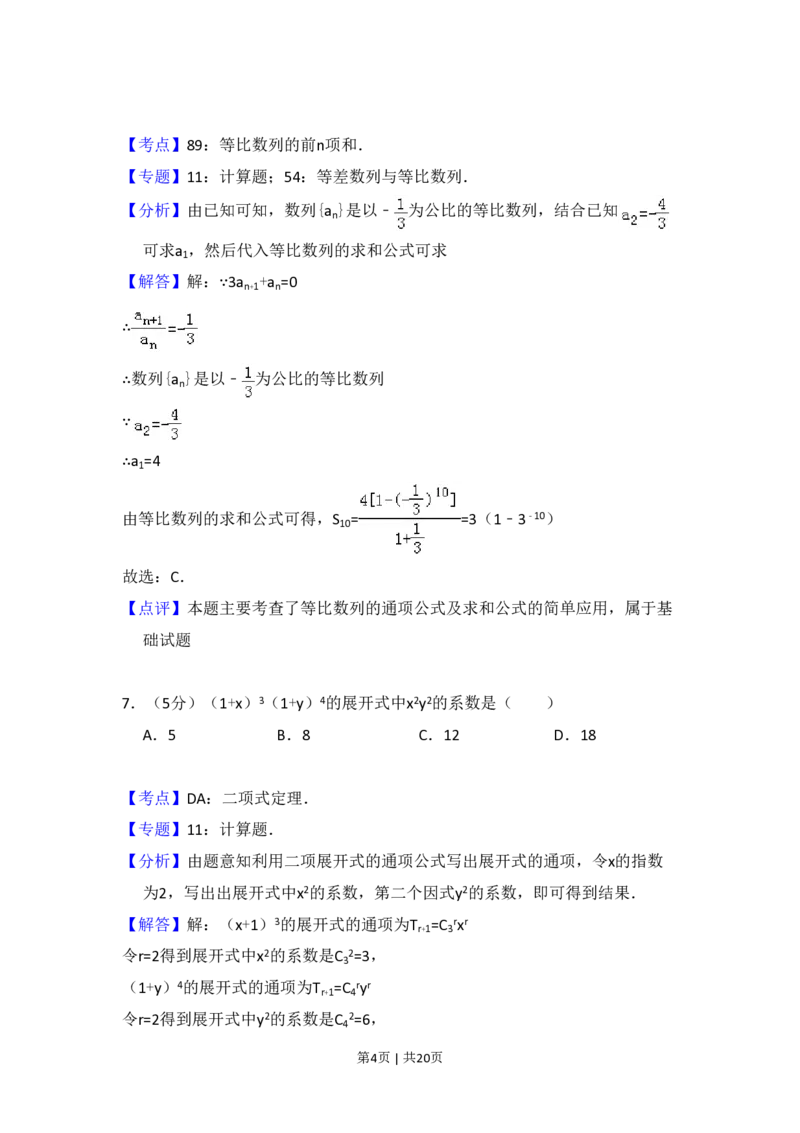
【分析】由已知可知,数列{a }是以﹣ 为公比的等比数列,结合已知
n
可求a ,然后代入等比数列的求和公式可求
1
【解答】解:∵3a +a =0
n+1 n
∴
∴数列{a }是以﹣ 为公比的等比数列
n
∵
∴a =4
1
由等比数列的求和公式可得,S = =3(1﹣3﹣10)
10
故选:C.
【点评】本题主要考查了等比数列的通项公式及求和公式的简单应用,属于基
础试题
7.(5分)(1+x)3(1+y)4的展开式中x2y2的系数是( )
A.5 B.8 C.12 D.18
【考点】DA:二项式定理.
菁优网版权所有
【专题】11:计算题.
【分析】由题意知利用二项展开式的通项公式写出展开式的通项,令x的指数
为2,写出出展开式中x2的系数,第二个因式y2的系数,即可得到结果.
【解答】解:(x+1)3的展开式的通项为T =C rxr
r+1 3
令r=2得到展开式中x2的系数是C 2=3,
3
(1+y)4的展开式的通项为T =C ryr
r+1 4
令r=2得到展开式中y2的系数是C 2=6,
4
第4页 | 共20页(1+x)3(1+y)4的展开式中x2y2的系数是:3×6=18,
故选:D.
【点评】本题考查利用二项展开式的通项公式解决二项展开式的特定项问题,
本题解题的关键是写出二项式的展开式,所有的这类问题都是利用通项来解
决的.
8.(5分)椭圆C: 的左、右顶点分别为A 、A ,点P在C上且直线PA
1 2 2
斜率的取值范围是[﹣2,﹣1],那么直线PA 斜率的取值范围是( )
1
A. B. C. D.
【考点】I3:直线的斜率;KH:直线与圆锥曲线的综合.
菁优网版权所有
【专题】5D:圆锥曲线的定义、性质与方程.
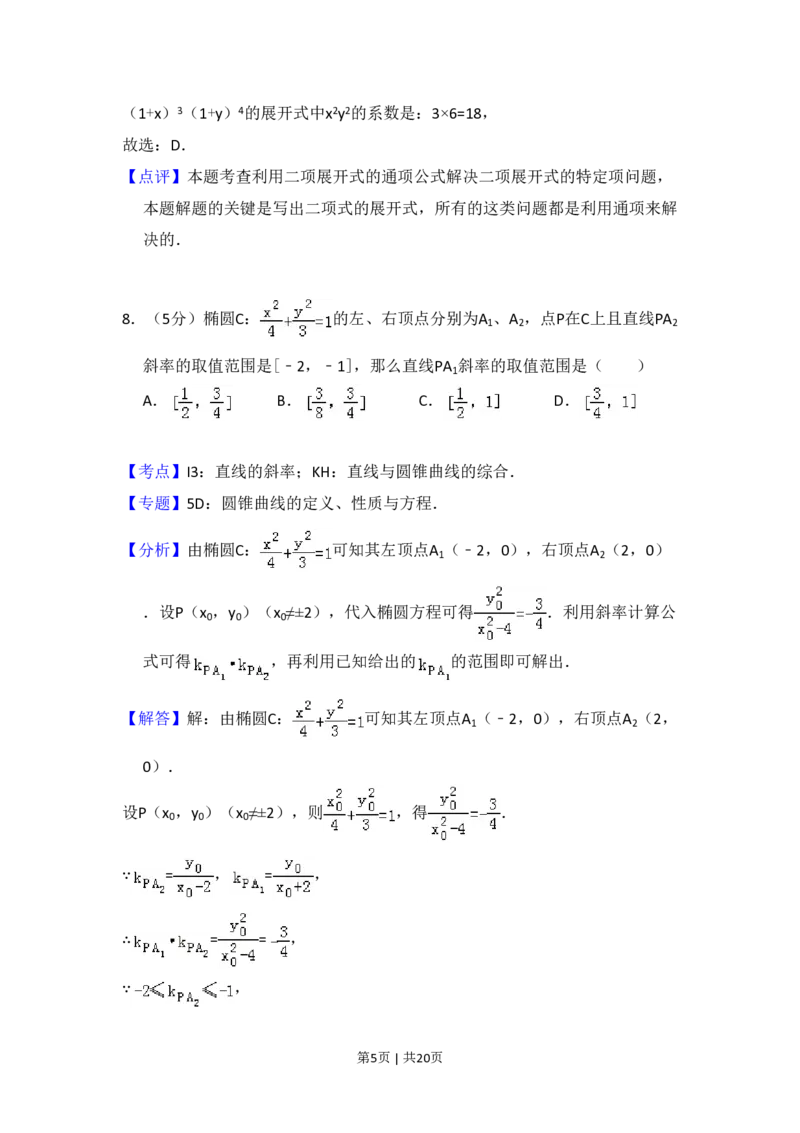
【分析】由椭圆C: 可知其左顶点A (﹣2,0),右顶点A (2,0)
1 2
.设P(x ,y )(x ≠±2),代入椭圆方程可得 .利用斜率计算公
0 0 0
式可得 ,再利用已知给出的 的范围即可解出.
【解答】解:由椭圆C: 可知其左顶点A (﹣2,0),右顶点A (2,
1 2
0).
设P(x ,y )(x ≠±2),则 ,得 .
0 0 0
∵ = , = ,
∴ = = ,
∵ ,
第5页 | 共20页∴ ,解得 .
故选:B.
【点评】熟练掌握椭圆的标准方程及其性质、斜率的计算公式、不等式的性质
等是解题的关键.
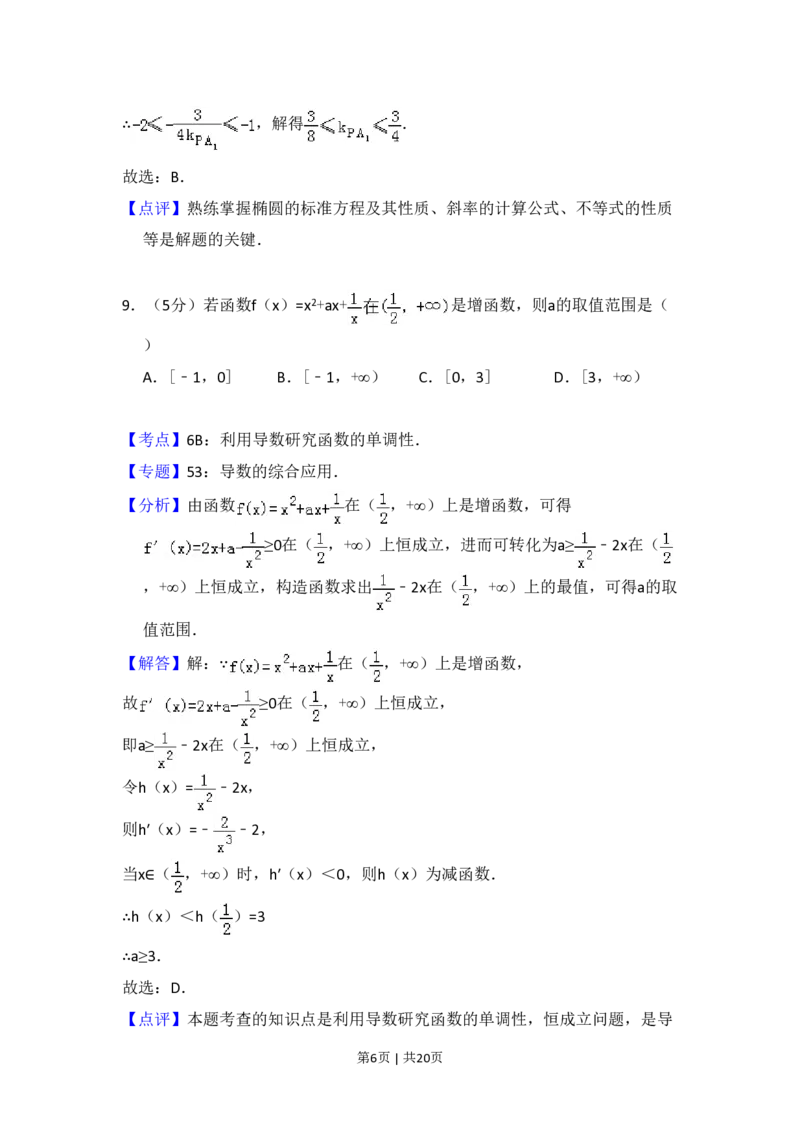
9.(5分)若函数f(x)=x2+ax+ 是增函数,则a的取值范围是(
)
A.[﹣1,0] B.[﹣1,+∞) C.[0,3] D.[3,+∞)
【考点】6B:利用导数研究函数的单调性.
菁优网版权所有
【专题】53:导数的综合应用.
【分析】由函数 在( ,+∞)上是增函数,可得
≥0在( ,+∞)上恒成立,进而可转化为a≥ ﹣2x在(
,+∞)上恒成立,构造函数求出 ﹣2x在( ,+∞)上的最值,可得a的取
值范围.
【解答】解:∵ 在( ,+∞)上是增函数,
故 ≥0在( ,+∞)上恒成立,
即a≥ ﹣2x在( ,+∞)上恒成立,
令h(x)= ﹣2x,
则h′(x)=﹣ ﹣2,
当x∈( ,+∞)时,h′(x)<0,则h(x)为减函数.
∴h(x)<h( )=3
∴a≥3.
故选:D.
【点评】本题考查的知识点是利用导数研究函数的单调性,恒成立问题,是导
第6页 | 共20页数的综合应用,难度中档.
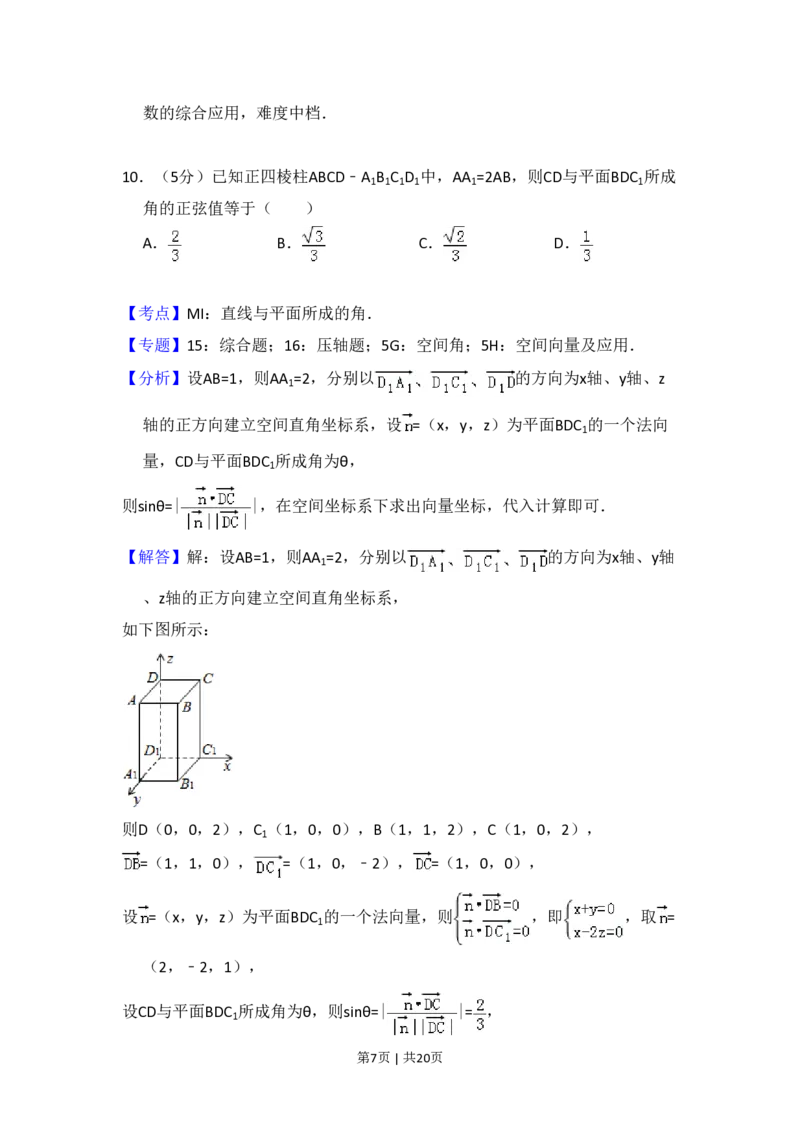
10.(5分)已知正四棱柱ABCD﹣A B C D 中,AA =2AB,则CD与平面BDC 所成
1 1 1 1 1 1
角的正弦值等于( )
A. B. C. D.
【考点】MI:直线与平面所成的角.
菁优网版权所有
【专题】15:综合题;16:压轴题;5G:空间角;5H:空间向量及应用.
【分析】设AB=1,则AA =2,分别以 的方向为x轴、y轴、z
1
轴的正方向建立空间直角坐标系,设 =(x,y,z)为平面BDC 的一个法向
1
量,CD与平面BDC 所成角为θ,
1
则sinθ=| |,在空间坐标系下求出向量坐标,代入计算即可.
【解答】解:设AB=1,则AA =2,分别以 的方向为x轴、y轴
1
、z轴的正方向建立空间直角坐标系,
如下图所示:
则D(0,0,2),C (1,0,0),B(1,1,2),C(1,0,2),
1
=(1,1,0), =(1,0,﹣2), =(1,0,0),
设 =(x,y,z)为平面BDC 的一个法向量,则 ,即 ,取 =
1
(2,﹣2,1),
设CD与平面BDC 所成角为θ,则sinθ=| |= ,
1
第7页 | 共20页故选:A.
【点评】本题考查直线与平面所成的角,考查空间向量的运算及应用,准确理
解线面角与直线方向向量、平面法向量夹角关系是解决问题的关键.
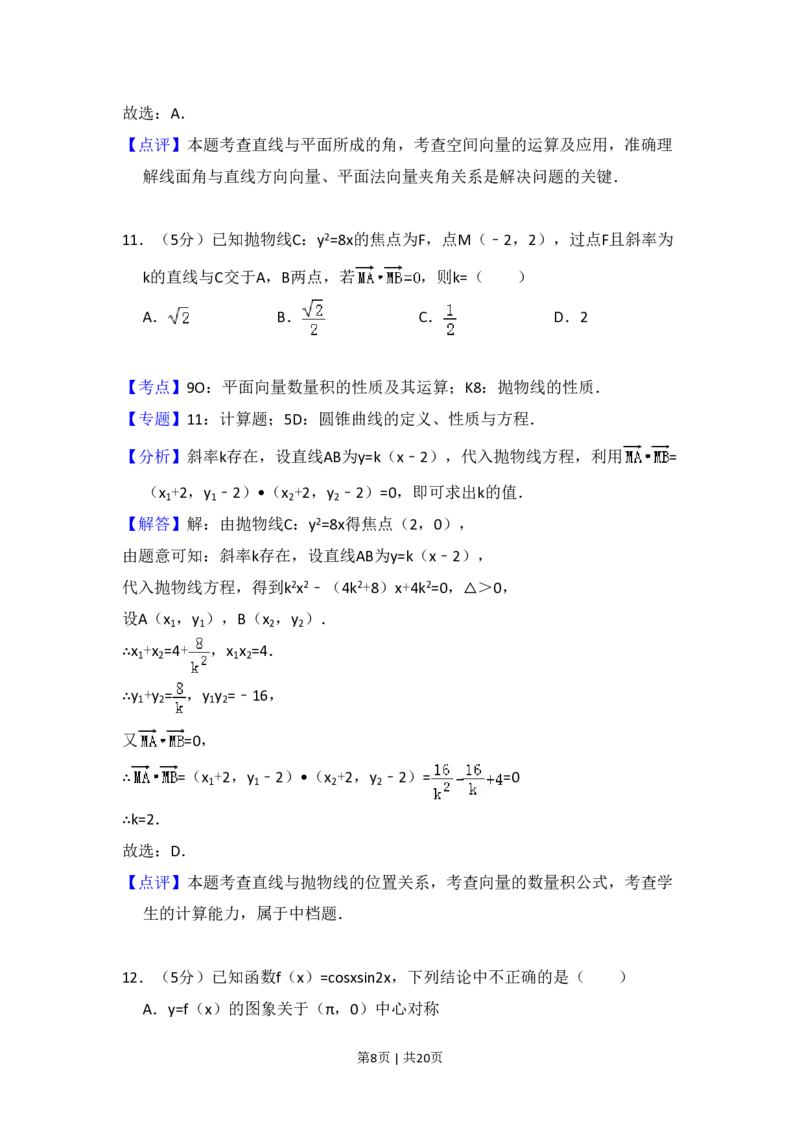
11.(5分)已知抛物线C:y2=8x的焦点为F,点M(﹣2,2),过点F且斜率为
k的直线与C交于A,B两点,若 ,则k=( )
A. B. C. D.2
【考点】9O:平面向量数量积的性质及其运算;K8:抛物线的性质.
菁优网版权所有
【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.
【分析】斜率k存在,设直线AB为y=k(x﹣2),代入抛物线方程,利用 =
(x +2,y ﹣2)•(x +2,y ﹣2)=0,即可求出k的值.
1 1 2 2
【解答】解:由抛物线C:y2=8x得焦点(2,0),
由题意可知:斜率k存在,设直线AB为y=k(x﹣2),
代入抛物线方程,得到k2x2﹣(4k2+8)x+4k2=0,△>0,
设A(x ,y ),B(x ,y ).
1 1 2 2
∴x +x =4+ ,x x =4.
1 2 1 2
∴y +y = ,y y =﹣16,
1 2 1 2
又 =0,
∴ =(x +2,y ﹣2)•(x +2,y ﹣2)= =0
1 1 2 2
∴k=2.
故选:D.
【点评】本题考查直线与抛物线的位置关系,考查向量的数量积公式,考查学
生的计算能力,属于中档题.
12.(5分)已知函数f(x)=cosxsin2x,下列结论中不正确的是( )
A.y=f(x)的图象关于(π,0)中心对称
第8页 | 共20页B.
C.
D.f(x)既是奇函数,又是周期函数
【考点】H1:三角函数的周期性;HW:三角函数的最值.
菁优网版权所有
【专题】11:计算题;57:三角函数的图像与性质.
【分析】根据函数图象关于某点中心对称或关于某条直线对称的公式,对A、B
两项加以验证,可得它们都正确.根据二倍角的正弦公式和同角三角函数的
关系化简,得f(x)=2sinx(1﹣sin2x),再换元:令t=sinx,得到关于t的三
次函数,利用导数研究此函数的单调性可得f(x)的最大值为 ,故C不
正确;根据函数周期性和奇偶性的定义加以验证,可得D项正确.由此可得
本题的答案.
【解答】解:对于A,因为f(π+x)=cos(π+x)sin(2π+2x)=﹣cosxsin2x,
f(π﹣x)=cos(π﹣x)sin(2π﹣2x)=cosxsin2x,所以f(π+x)+f(π﹣x)=0,
可得y=f(x)的图象关于(π,0)中心对称,故A正确;
对于B,因为f( +x)=cos( +x)sin(π+2x)=﹣sinx(﹣sin2x)=sinxsin2x
,
f( ﹣x)=cos( ﹣x)sin(π﹣2x)=sinxsin2x,所以f( +x)=f( ﹣x
),
可得y=f(x)的图象关于直线x= 对称,故B正确;
对于C,化简得f(x)=cosxsin2x=2cos2xsinx=2sinx(1﹣sin2x),
令t=sinx,f(x)=g(t)=2t(1﹣t2),﹣1≤t≤1,
∵g(t)=2t(1﹣t2)的导数g'(t)=2﹣6t2=2(1+ t)(1﹣ t)
∴当t∈(﹣1,﹣ )时或t∈( ,1)时g'(t)<0,函数g(t)为减函数;
当t∈(﹣ , )时g'(t)>0,函数g(t)为增函数.
因此函数g(t)的最大值为t=﹣1时或t= 时的函数值,
第9页 | 共20页结合g(﹣1)=0<g( )= ,可得g(t)的最大值为 .
由此可得f(x)的最大值为 而不是 ,故C不正确;
对于D,因为f(﹣x)=cos(﹣x)sin(﹣2x)=﹣cosxsin2x=﹣f(x),所以f(x
)是奇函数.
因为f(2π+x)=cos(2π+x)sin(4π+2x)=cosxsin2x=f(x),
所以2π为函数的一个周期,得f(x)为周期函数.可得f(x)既是奇函数,又
是周期函数,得D正确.
综上所述,只有C项不正确.
故选:C.
【点评】本题给出三角函数式,研究函数的奇偶性、单调性和周期性.着重考
查了三角恒等变换公式、利用导数研究函数的单调性和函数图象的对称性等
知识,属于中档题.
二、填空题:本大题共4小题,每小题5分.
13.(5分)已知α是第三象限角,sinα=﹣ ,则cotα= 2 .
【考点】GG:同角三角函数间的基本关系.
菁优网版权所有
【专题】56:三角函数的求值.
【分析】根据α是第三象限的角,得到cosα小于0,然后由sinα的值,利用同角
三角函数间的基本关系求出cosα的值,进而求出cotα的值.
【解答】解:由α是第三象限的角,得到cosα<0,
又sinα=﹣ ,所以cosα=﹣ =﹣
则cotα= =2
故答案为:2
【点评】此题考查学生灵活运用同角三角函数间的基本关系化简求值,是一道
基础题.学生做题时注意α的范围.
14.(5分)6个人排成一行,其中甲、乙两人不相邻的不同排法共有 480
第10页 | 共20页种.(用数字作答)
【考点】D9:排列、组合及简单计数问题.
菁优网版权所有
【专题】11:计算题.
【分析】排列好甲、乙两人外的4人,然后把甲、乙两人插入4个人的5个空位
中即可.
【解答】解:6个人排成一行,其中甲、乙两人不相邻的不同排法:排列好甲
、乙两人外的4人,有 中方法,
然后把甲、乙两人插入4个人的5个空位,有 种方法,
所以共有: =480.
故答案为:480.
【点评】本题考查了乘法原理,以及排列的简单应用,插空法解答不相邻问题
.
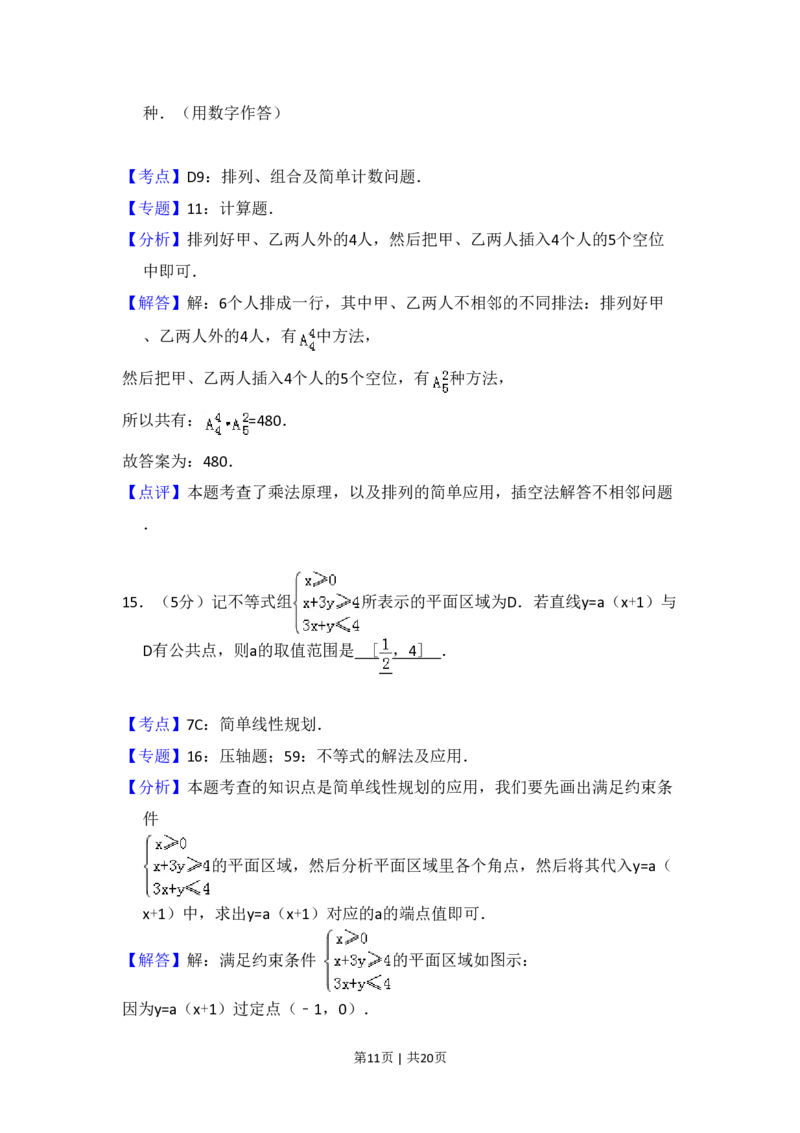
15.(5分)记不等式组 所表示的平面区域为D.若直线y=a(x+1)与
D有公共点,则a的取值范围是 [ ,4] .
【考点】7C:简单线性规划.
菁优网版权所有
【专题】16:压轴题;59:不等式的解法及应用.
【分析】本题考查的知识点是简单线性规划的应用,我们要先画出满足约束条
件
的平面区域,然后分析平面区域里各个角点,然后将其代入y=a(
x+1)中,求出y=a(x+1)对应的a的端点值即可.
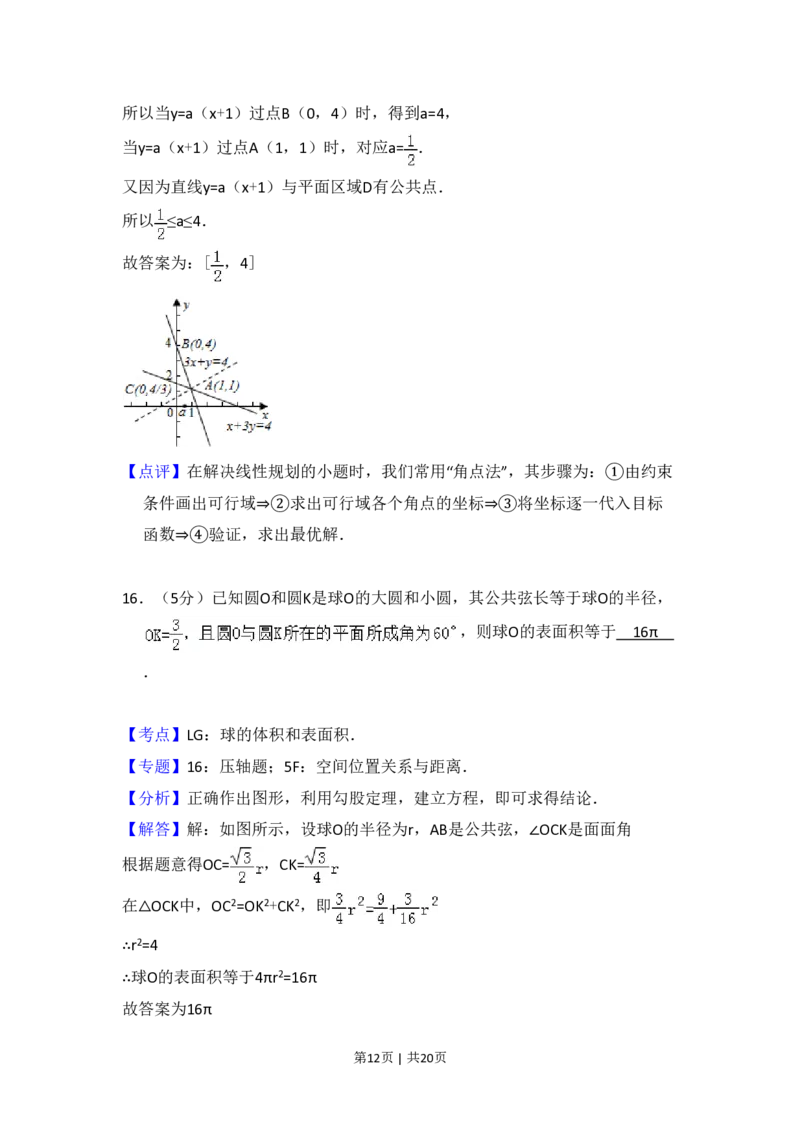
【解答】解:满足约束条件 的平面区域如图示:
因为y=a(x+1)过定点(﹣1,0).
第11页 | 共20页所以当y=a(x+1)过点B(0,4)时,得到a=4,
当y=a(x+1)过点A(1,1)时,对应a= .
又因为直线y=a(x+1)与平面区域D有公共点.
所以 ≤a≤4.
故答案为:[ ,4]
【点评】在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束
条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标
函数⇒④验证,求出最优解.
16.(5分)已知圆O和圆K是球O的大圆和小圆,其公共弦长等于球O的半径,
,则球O的表面积等于 16π
.
【考点】LG:球的体积和表面积.
菁优网版权所有
【专题】16:压轴题;5F:空间位置关系与距离.
【分析】正确作出图形,利用勾股定理,建立方程,即可求得结论.
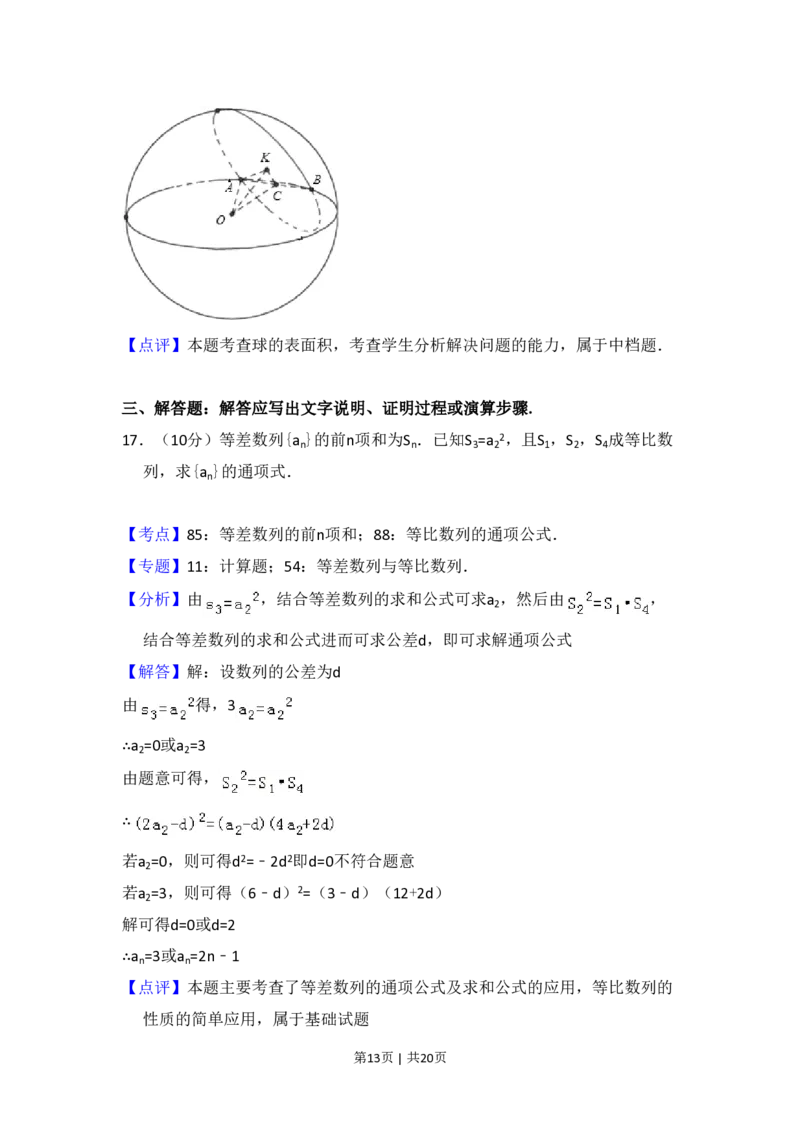
【解答】解:如图所示,设球O的半径为r,AB是公共弦,∠OCK是面面角
根据题意得OC= ,CK=
在△OCK中,OC2=OK2+CK2,即
∴r2=4
∴球O的表面积等于4πr2=16π
故答案为16π
第12页 | 共20页【点评】本题考查球的表面积,考查学生分析解决问题的能力,属于中档题.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(10分)等差数列{a }的前n项和为S .已知S =a 2,且S ,S ,S 成等比数
n n 3 2 1 2 4
列,求{a }的通项式.
n
【考点】85:等差数列的前n项和;88:等比数列的通项公式.
菁优网版权所有
【专题】11:计算题;54:等差数列与等比数列.
【分析】由 ,结合等差数列的求和公式可求a ,然后由 ,
2
结合等差数列的求和公式进而可求公差d,即可求解通项公式
【解答】解:设数列的公差为d
由 得,3
∴a =0或a =3
2 2
由题意可得,
∴
若a =0,则可得d2=﹣2d2即d=0不符合题意
2
若a =3,则可得(6﹣d)2=(3﹣d)(12+2d)
2
解可得d=0或d=2
∴a =3或a =2n﹣1
n n
【点评】本题主要考查了等差数列的通项公式及求和公式的应用,等比数列的
性质的简单应用,属于基础试题
第13页 | 共20页18.(12分)设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c
)(a﹣b+c)=ac.
(Ⅰ)求B.
(Ⅱ)若sinAsinC= ,求C.
【考点】GP:两角和与差的三角函数;HR:余弦定理.
菁优网版权所有
【专题】58:解三角形.
【分析】(I)已知等式左边利用多项式乘多项式法则计算,整理后得到关系式
,利用余弦定理表示出cosB,将关系式代入求出cosB的值,由B为三角形的
内角,利用特殊角的三角函数值即可求出B的度数;
(II)由(I)得到A+C的度数,利用两角和与差的余弦函数公式化简cos(A﹣C
),变形后将cos(A+C)及2sinAsinC的值代入求出cos(A﹣C)的值,利用
特殊角的三角函数值求出A﹣C的值,与A+C的值联立即可求出C的度数.
【解答】解:(I)∵(a+b+c)(a﹣b+c)=(a+c)2﹣b2=ac,
∴a2+c2﹣b2=﹣ac,
∴cosB= =﹣ ,
又B为三角形的内角,
则B=120°;
(II)由(I)得:A+C=60°,∵sinAsinC= ,cos(A+C)= ,
∴cos(A﹣C)=cosAcosC+sinAsinC=cosAcosC﹣sinAsinC+2sinAsinC=cos(A+C)+2s
inAsinC= +2× = ,
∴A﹣C=30°或A﹣C=﹣30°,
则C=15°或C=45°.
【点评】此题考查了余弦定理,两角和与差的余弦函数公式,以及特殊角的三
角函数值,熟练掌握余弦定理是解本题的关键.
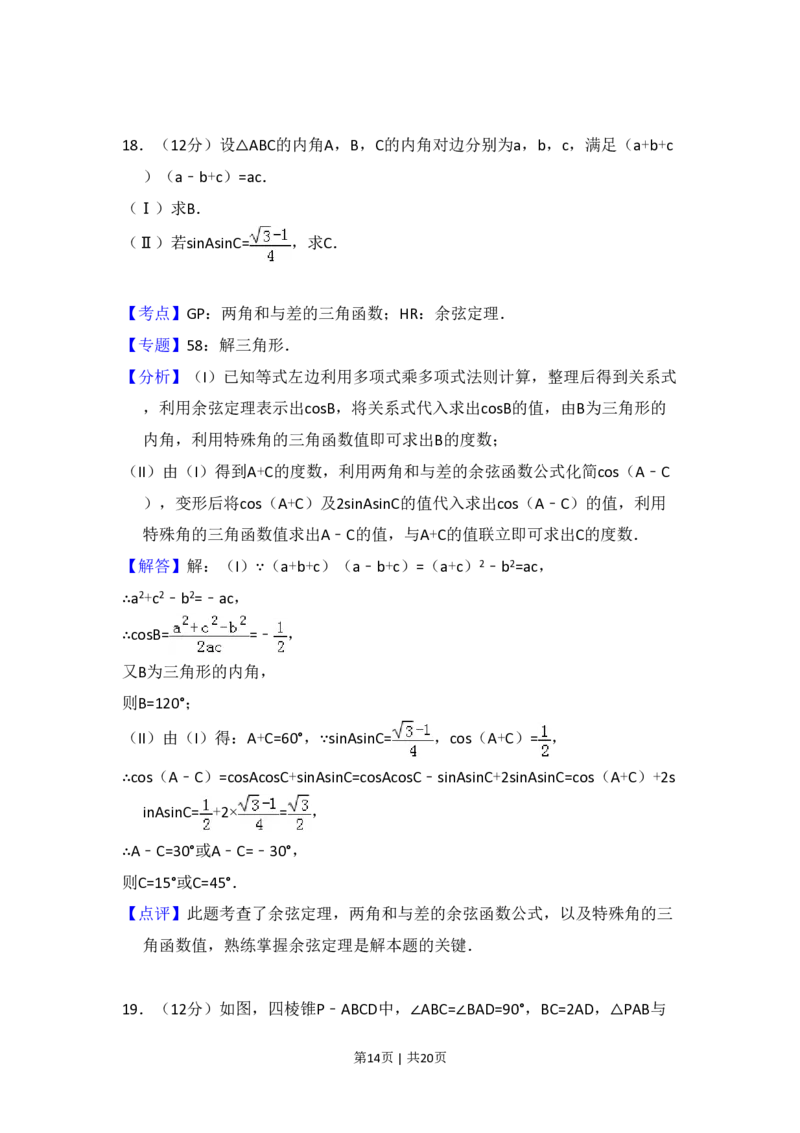
19.(12分)如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与
第14页 | 共20页△PAD都是等边三角形.
(Ⅰ)证明:PB⊥CD;
(Ⅱ)求二面角A﹣PD﹣C的大小.
【考点】LW:直线与平面垂直;M5:共线向量与共面向量.
菁优网版权所有
【专题】11:计算题;5G:空间角.
【分析】(I)取BC的中点E,连接DE,过点P作PO⊥平面ABCD于O,连接OA、O
B、OD、OE.可证出四边形ABED是正方形,且O为正方形ABED的中心.因
此OE⊥OB,结合三垂线定理,证出OE⊥PB,而OE是△BCD的中位线,可得OE
∥CD,因此PB⊥CD;
(II)由(I)的结论,证出CD⊥平面PBD,从而得到CD⊥PD.取PD的中点F,PC
的中点G,连接FG,可得FG∥CD,所以FG⊥PD.连接AF,可得AF⊥PD,因此∠
AFG为二面角A﹣PD﹣C的平面角,连接AG、EG,则EG∥PB,可得EG⊥OE.设
AB=2,可求出AE、EG、AG、AF和FG的长,最后在△AFG中利用余弦定理,
算出∠AFG=π﹣arccos ,即得二面角A﹣PD﹣C的平面角大小.
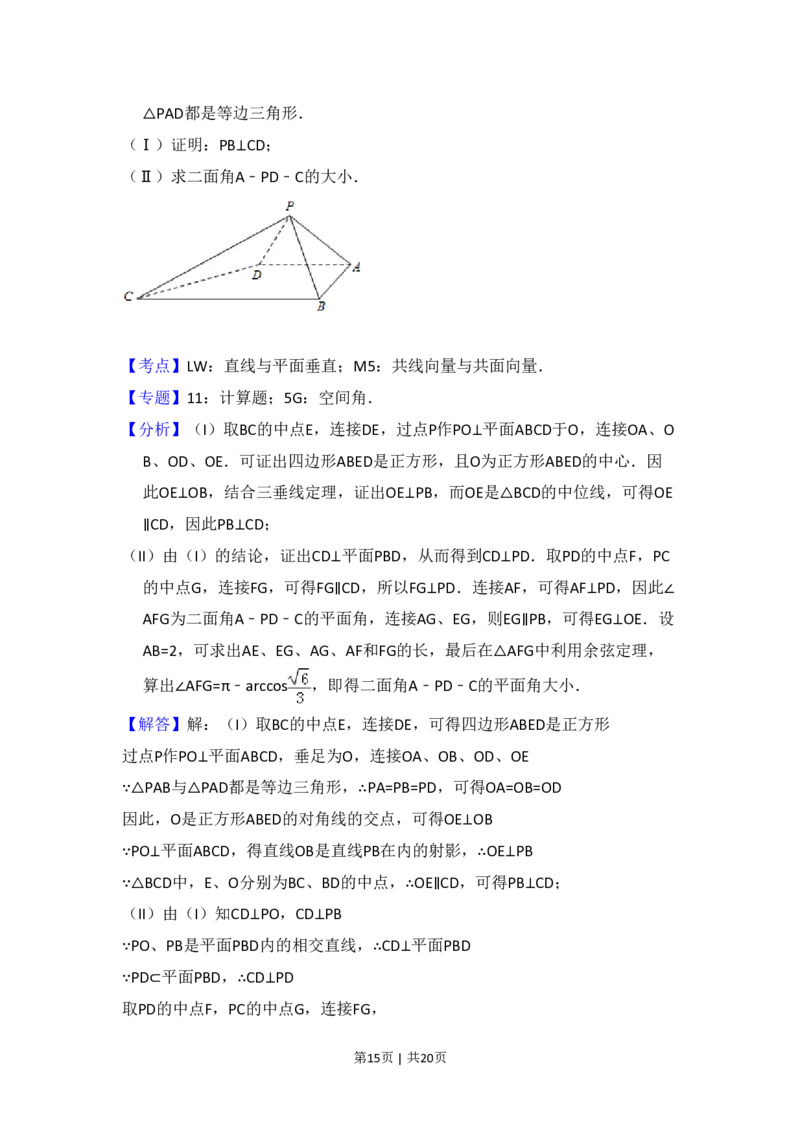
【解答】解:(I)取BC的中点E,连接DE,可得四边形ABED是正方形
过点P作PO⊥平面ABCD,垂足为O,连接OA、OB、OD、OE
∵△PAB与△PAD都是等边三角形,∴PA=PB=PD,可得OA=OB=OD
因此,O是正方形ABED的对角线的交点,可得OE⊥OB
∵PO⊥平面ABCD,得直线OB是直线PB在内的射影,∴OE⊥PB
∵△BCD中,E、O分别为BC、BD的中点,∴OE∥CD,可得PB⊥CD;
(II)由(I)知CD⊥PO,CD⊥PB
∵PO、PB是平面PBD内的相交直线,∴CD⊥平面PBD
∵PD⊂平面PBD,∴CD⊥PD
取PD的中点F,PC的中点G,连接FG,
第15页 | 共20页则FG为△PCD有中位线,∴FG∥CD,可得FG⊥PD
连接AF,由△PAD是等边三角形可得AF⊥PD,∴∠AFG为二面角A﹣PD﹣C的平面
角
连接AG、EG,则EG∥PB
∵PB⊥OE,∴EG⊥OE,
设AB=2,则AE=2 ,EG= PB=1,故AG= =3
在△AFG中,FG= CD= ,AF= ,AG=3
∴cos∠AFG= =﹣ ,得∠AFG=π﹣arccos ,
即二面角A﹣PD﹣C的平面角大小是π﹣arccos .
【点评】本题给出特殊的四棱锥,求证直线与直线垂直并求二面角平面角的大
小,着重考查了线面垂直的判定与性质、三垂线定理和运用余弦定理求二面
的大小等知识,属于中档题.
20.(12分)甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁
判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率
均为 ,各局比赛的结果都相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.
【考点】CB:古典概型及其概率计算公式;CH:离散型随机变量的期望与方差
.
菁优网版权所有
【专题】5I:概率与统计.
【分析】(I)令A 表示第2局结果为甲获胜,A 表示第3局甲参加比赛时,结果
1 2
为甲负,A表示第4局甲当裁判,分析其可能情况,每局比赛的结果相互独
第16页 | 共20页立且互斥,利用独立事件、互斥事件的概率求解即可.
(II)X的所有可能值为0,1,2.分别求出X取每一个值的概率,列出分布列后
求出期望值即可.
【解答】解:(I)令A 表示第2局结果为甲获胜.A 表示第3局甲参加比赛时,
1 2
结果为甲负.A表示第4局甲当裁判.
则A=A •A ,P(A)=P(A •A )=P(A )P(A )= ;
1 2 1 2 1 2
(Ⅱ)X的所有可能值为0,1,2.令A 表示第3局乙和丙比赛时,结果为乙胜
3
.
B 表示第1局结果为乙获胜,B 表示第2局乙和甲比赛时,结果为乙胜,B 表示
1 2 3
第3局乙参加比赛时,结果为乙负,
则P(X=0)=P(B B )=P(B )P(B )P( )= .
1 2 1 2
P(X=2)=P( B )=P( )P(B )= .
3 3
P(X=1)=1﹣P(X=0)﹣P(X=2)= .
从而EX=0× +1× +2× = .
【点评】本题考查互斥、独立事件的概率,离散型随机变量的分布列和期望等
知识,同时考查利用概率知识解决问题的能力.
21.(12分)已知双曲线C: =1(a>0,b>0)的左、右焦点分别为F
1
,F ,离心率为3,直线y=2与C的两个交点间的距离为 .
2
(I)求a,b;
(II)设过F 的直线l与C的左、右两支分别相交于A、B两点,且|AF |=|BF |,
2 1 1
证明:|AF |、|AB|、|BF |成等比数列.
2 2
【考点】K4:椭圆的性质;KH:直线与圆锥曲线的综合.
菁优网版权所有
【专题】14:证明题;15:综合题;16:压轴题;35:转化思想;5D:圆锥曲
线的定义、性质与方程.
【分析】(I)由题设,可由离心率为3得到参数a,b的关系,将双曲线的方程
第17页 | 共20页用参数a表示出来,再由直线 建立方程求出
参数a即可得到双曲线的方程;
(II)由(I)的方程求出两焦点坐标,设出直线l的方程设A(x ,y ),B(x
1 1 2
,y ),将其与双曲线C的方程联立,得出x +x = , ,再
2 1 2
利用|AF |=|BF |建立关于A,B坐标的方程,得出两点横坐标的关系
1 1
,由此方程求出k的值,得出直线的方程,从而可求得:|AF |、
2
|AB|、|BF |,再利用等比数列的性质进行判断即可证明出结论.
2
【解答】解:(I)由题设知 =3,即 =9,故b2=8a2
所以C的方程为8x2﹣y2=8a2
将y=2代入上式,并求得x=± ,
由题设知,2 = ,解得a2=1
所以a=1,b=2
(II)由(I)知,F (﹣3,0),F (3,0),C的方程为8x2﹣y2=8 ①
1 2
由题意,可设l的方程为y=k(x﹣3),|k|<2 代入①并化简得(k2﹣8)x2﹣
6k2x+9k2+8=0
设A(x ,y ),B(x ,y ),
1 1 2 2
则x ≤﹣1,x ≥1,x +x = , ,于是
1 2 1 2
|AF |= =﹣(3x +1),
1 1
|BF |= =3x +1,
1 2
|AF |=|BF |得﹣(3x +1)=3x +1,即
1 1 1 2
故 = ,解得 ,从而 =﹣
由于|AF |= =1﹣3x ,
2 1
第18页 | 共20页|BF |= =3x ﹣1,
2 2
故|AB|=|AF |﹣|BF |=2﹣3(x +x )=4,|AF ||BF |=3(x +x )﹣9x x ﹣1=16
2 2 1 2 2 2 1 2 1 2
因而|AF ||BF |=|AB|2,所以|AF |、|AB|、|BF |成等比数列
2 2 2 2
【点评】本题考查直线与圆锥曲线的综合关系,考查了运算能力,题设条件的
转化能力,方程的思想运用,此类题综合性强,但解答过程有其固有规律,
一般需要把直线与曲线联立利用根系关系,解答中要注意提炼此类题解答过
程中的共性,给以后解答此类题提供借鉴.
22.(12分)已知函数 .
(I)若x≥0时,f(x)≤0,求λ的最小值;
(II)设数列{a }的通项a =1+ .
n n
【考点】6E:利用导数研究函数的最值;8E:数列的求和;8K:数列与不等式
的综合.
菁优网版权所有
【专题】16:压轴题;35:转化思想;53:导数的综合应用;54:等差数列与
等比数列.
【分析】(I)由于已知函数的最大值是0,故可先求出函数的导数,研究其单
调性,确定出函数的最大值,利用最大值小于等于0求出参数λ的取值范围,
即可求得其最小值;
(II)根据(I)的证明,可取λ= ,由于x>0时,f(x)<0得出
,考察发现,若取x= ,则可得出 ,
以此为依据,利用放缩法,即可得到结论
【解答】解:(I)由已知,f(0)=0,
f′(x)= = ,
∴f′(0)=0
欲使x≥0时,f(x)≤0恒成立,则f(x)在(0,+∞)上必为减函数,即在(0,
+∞)上f′(x)<0恒成立,
第19页 | 共20页当λ≤0时,f′(x)>0在(0,+∞)上恒成立,为增函数,故不合题意,
若0<λ< 时,由f′(x)>0解得x< ,则当0<x< ,f′(x)>0,
所以当0<x< 时,f(x)>0,此时不合题意,
若λ≥ ,则当x>0时,f′(x)<0恒成立,此时f(x)在(0,+∞)上必为减函
数,所以当x>0时,f(x)<0
恒成立,
综上,符合题意的λ的取值范围是λ≥ ,即λ的最小值为
( II)令λ= ,由(I)知,当x>0时,f(x)<0,即
取x= ,则
于是a ﹣a + = + +…+ +
2n n
=
=
=
= > =ln2n﹣lnn=ln2
所以
【点评】本题考查了数列中证明不等式的方法及导数求最值的普通方法,解题
的关键是充分利用已有的结论再结合放缩法,本题考查了推理判断的能力及
转化化归的思想,有一定的难度
第20页 | 共20页