文档内容
2013年北京市高考数学试卷(理科)
一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出
符合题目要求的一项.
1.(5分)已知集合A={﹣1,0,1},B={x|﹣1≤x<1},则A∩B=( )
A.{0} B.{﹣1,0} C.{0,1} D.{﹣1,0,1}
2.(5分)在复平面内,复数(2﹣i)2对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(5分)“φ=π”是“曲线y=sin(2x+φ)过坐标原点”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
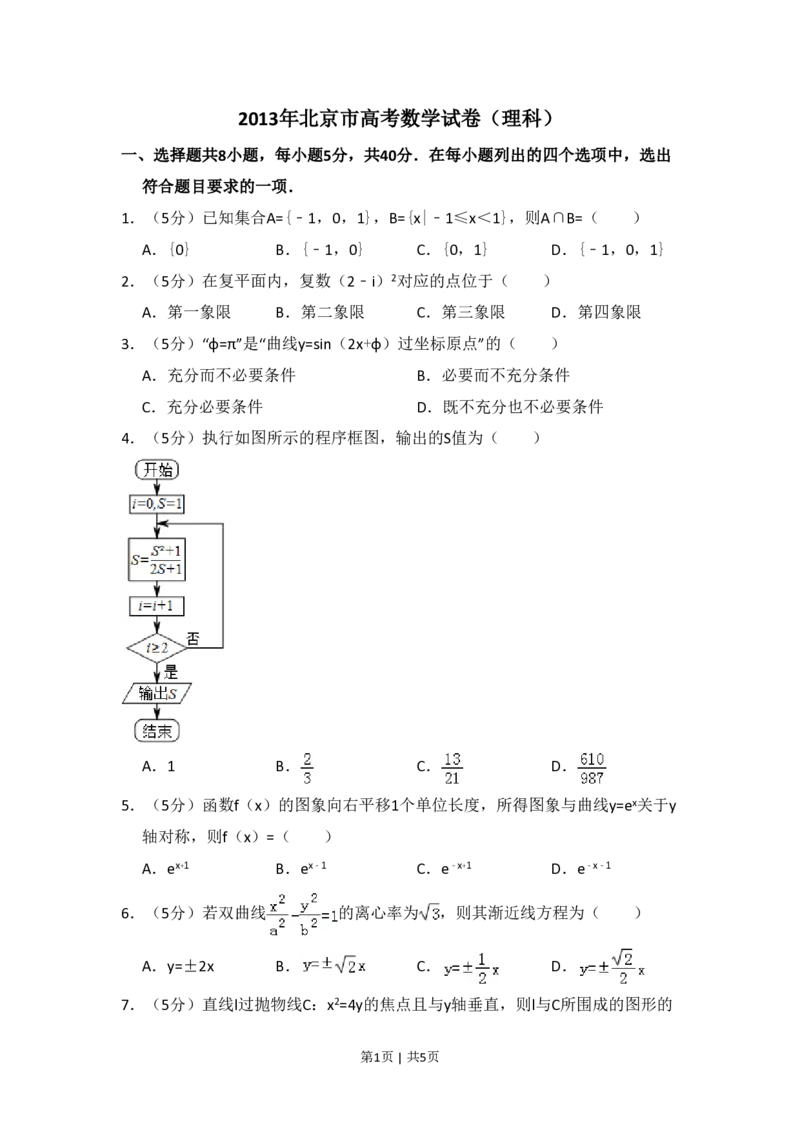
4.(5分)执行如图所示的程序框图,输出的S值为( )
A.1 B. C. D.
5.(5分)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y
轴对称,则f(x)=( )
A.ex+1 B.ex﹣1 C.e﹣x+1 D.e﹣x﹣1
6.(5分)若双曲线 的离心率为 ,则其渐近线方程为( )
A.y=±2x B. C. D.
7.(5分)直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的
第1页 | 共5页面积等于( )
A. B.2 C. D.
8.(5分)设关于x,y的不等式组 表示的平面区域内存在点P
(x ,y ),满足x ﹣2y =2,求得m的取值范围是( )
0 0 0 0
A. B. C. D.
二、填空题共6小题,每小题5分,共30分.
9.(5分)在极坐标系中,点(2, )到直线ρsinθ=2的距离等于 .
10.(5分)若等比数列{a }满足a +a =20,a +a =40,则公比q=
n 2 4 3 5
;前n项和S = .
n
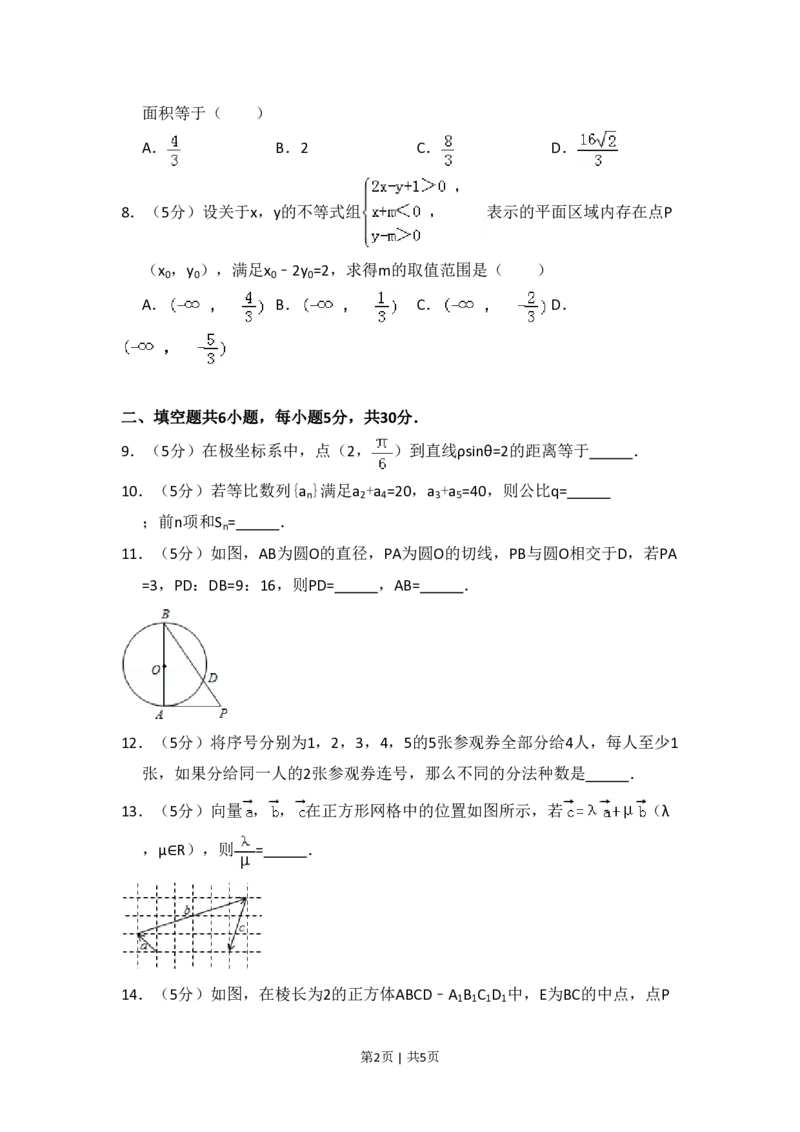
11.(5分)如图,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D,若PA
=3,PD:DB=9:16,则PD= ,AB= .
12.(5分)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1
张,如果分给同一人的2张参观券连号,那么不同的分法种数是 .
13.(5分)向量 , , 在正方形网格中的位置如图所示,若 (λ
,μ∈R),则 = .
14.(5分)如图,在棱长为2的正方体ABCD﹣A B C D 中,E为BC的中点,点P
1 1 1 1
第2页 | 共5页在线段D E上,点P到直线CC 的距离的最小值为 .
1 1
三、解答题共6小题,共50分.解答应写出文字说明,演算步骤
15.(13分)在△ABC中,a=3,b=2 ,∠B=2∠A.
(Ⅰ)求cosA的值;
(Ⅱ)求c的值.
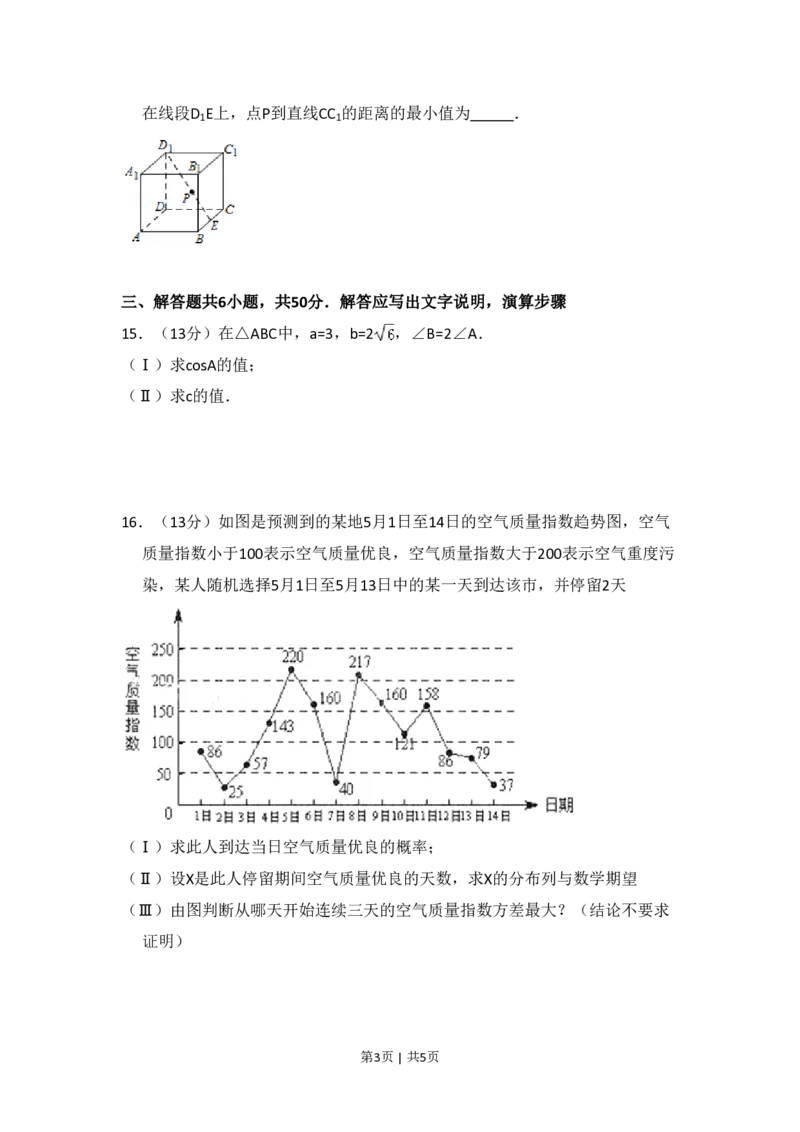
16.(13分)如图是预测到的某地5月1日至14日的空气质量指数趋势图,空气
质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污
染,某人随机选择5月1日至5月13日中的某一天到达该市,并停留2天
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求
证明)
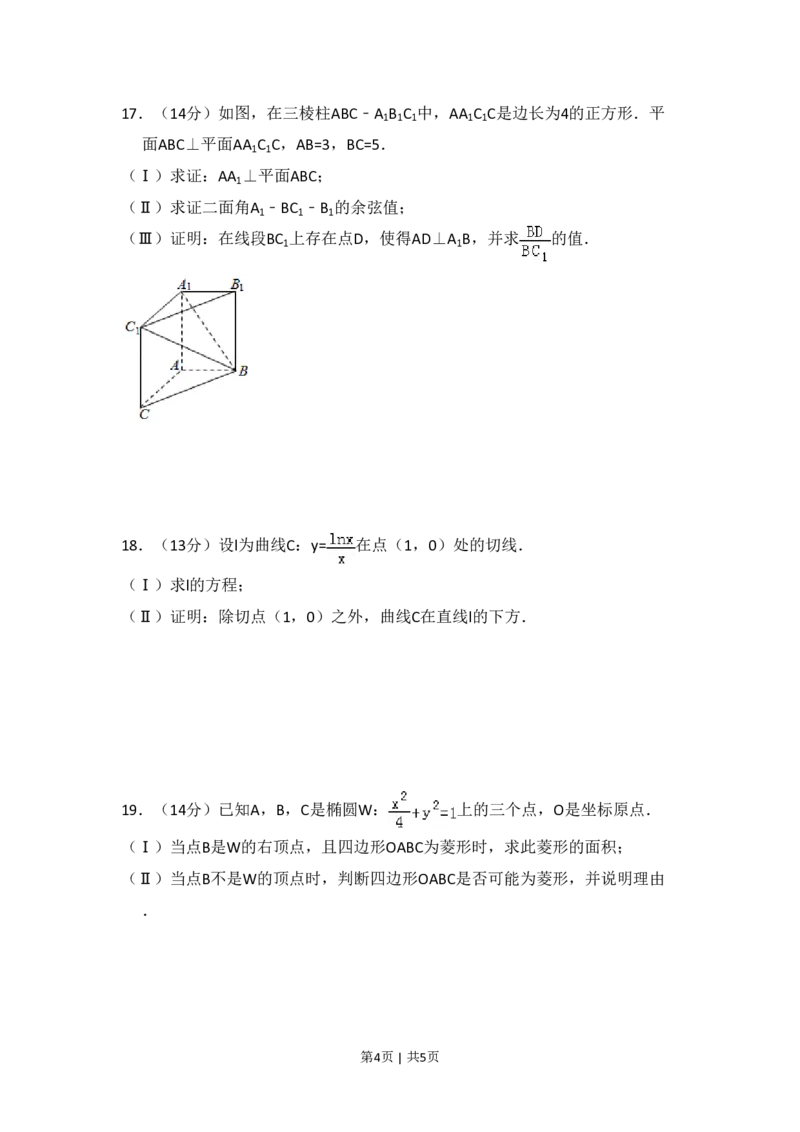
第3页 | 共5页17.(14分)如图,在三棱柱ABC﹣A B C 中,AA C C是边长为4的正方形.平
1 1 1 1 1
面ABC⊥平面AA C C,AB=3,BC=5.
1 1
(Ⅰ)求证:AA ⊥平面ABC;
1
(Ⅱ)求证二面角A ﹣BC ﹣B 的余弦值;
1 1 1
(Ⅲ)证明:在线段BC 上存在点D,使得AD⊥A B,并求 的值.
1 1
18.(13分)设l为曲线C:y= 在点(1,0)处的切线.
(Ⅰ)求l的方程;
(Ⅱ)证明:除切点(1,0)之外,曲线C在直线l的下方.
19.(14分)已知A,B,C是椭圆W: 上的三个点,O是坐标原点.
(Ⅰ)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(Ⅱ)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由
.
第4页 | 共5页20.(13分)已知{a }是由非负整数组成的无穷数列,该数列前n项的最大值记
n
为A ,第n项之后各项a ,a …的最小值记为B ,d =A ﹣B .
n n+1 n+2 n n n n
(Ⅰ)若{a }为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意n
n
∈N*,a =a ),写出d ,d ,d ,d 的值;
n+4 n 1 2 3 4
(Ⅱ)设d是非负整数,证明:d =﹣d(n=1,2,3…)的充分必要条件为{a }是
n n
公差为d的等差数列;
(Ⅲ)证明:若a =2,d =1(n=1,2,3,…),则{a }的项只能是1或者2,且
1 n n
有无穷多项为1.
第5页 | 共5页