文档内容
2013年上海市秋季高考理科数学
一、填空题
n+20
1.计算:lim = ______
n®¥3n+13
n+20 1
【解答】根据极限运算法则,lim = .
n®¥3n+13 3
2.设mÎR,m2 +m-2+(m2 -1)i是纯虚数,其中i是虚数单位,则m= ________
ìm2 +m-2=0
【解答】í Þm=-2.
î m2 -1¹0
x2 y2 x x
3.若 = ,则x+ y = ______
-1 1 y -y
【解答】x2 + y2 =-2xyÞ x+ y =0.
4.已知△ABC的内角A、B、C所对应边分别为a、b、c,若3a2 +2ab+3b2 -3c2 =0,则
角C的大小是_______________(结果用反三角函数值表示)
2
【解答】3a2 +2ab+3b2 -3c2 =0Þc2 =a2 +b2 + ab,故
3
1 1
cosC =- ,C =p-arccos .
3 3
5
æ aö
5.设常数aÎR,若ç x2 +
÷
的二项展开式中x7项的系数为-10,则a= ______
è xø
a
【解答】T =Cr(x2)5-r( )r,2(5-r)-r =7Þr =1,故C1a=-10Þa=-2.
r+1 5 x 5
3 1
6.方程 + =3x-1的实数解为________
3x -1 3
【解答】原方程整理后变为32x -2×3x -8=0Þ3x =4Þ x=log 4.
3
7.在极坐标系中,曲线r=cosq+1与rcosq=1的公共点到极点的距离为__________
1± 5 1+ 5
【解答】联立方程组得r(r-1)=1Þr= ,又r³0,故所求为 .
2 2
8.盒子中装有编号为1,2,3,4,5,6,7,8,9的九个球,从中任意取出两个,则这两
个球的编号之积为偶数的概率是___________(结果用最简分数表示)
C2 13
【解答】9个数5个奇数,4个偶数,根据题意所求概率为1- 5 = .
C2 18
9
p
9.设AB是椭圆G的长轴,点C在G上,且ÐCBA= ,若AB=4,BC = 2,则G的两
4
个焦点之间的距离为________
x2 y2
【解答】不妨设椭圆G的标准方程为 + =1,于是可算得C(1,1),得
4 b2
4 4 6
b2 = ,2c= .
3 3
10.设非零常数d是等差数列x ,x ,x , ,x 的公差,随机变量x等可能地取值
1 2 3 L 19
x ,x ,x , ,x ,则方差Dx= _______
1 2 3 L 19
第1页 | 共8页d2
【解答】Ex= x ,Dx= (92 +82 + +12 +02 +12 + +92) = 30|d |.
10 19 L L
1 2
11.若cosxcosy+sinxsin y = ,sin2x+sin2y = ,则sin(x+ y)= ________
2 3
1 2
【解答】cos(x- y)= ,sin2x+sin2y =2sin(x+ y)cos(x- y)= ,故
2 3
2
sin(x+ y)= .
3
a2
12.设a为实常数,y = f(x)是定义在R上的奇函数,当x<0时, f(x)=9x+ +7,
x
若 f(x)³a+1对一切x³0成立,则a的取值范围为________
a2
【解答】 f(0)=0,故0³a+1Þa£-1;当x>0时, f(x)=9x+ -7³a+1
x
8
即6|a|³a+8,又a£-1,故a£- .
7
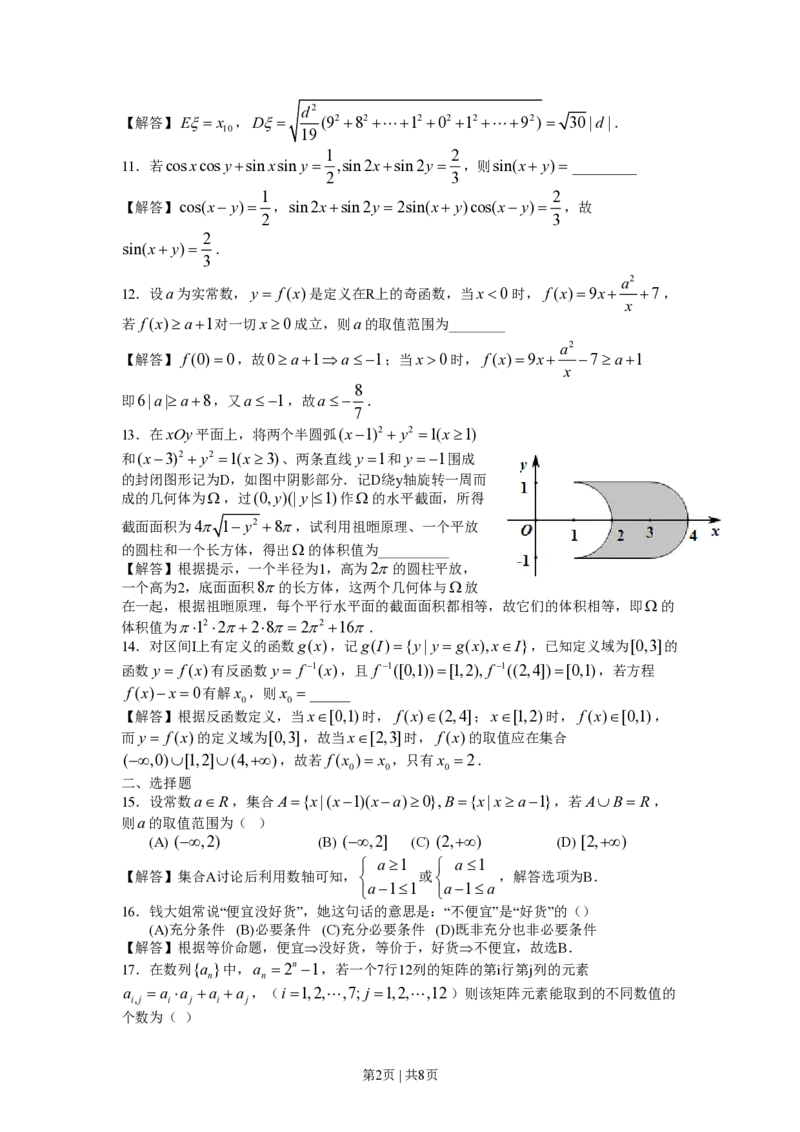
13.在xOy平面上,将两个半圆弧(x-1)2 + y2 =1(x³1)
和(x-3)2 + y2 =1(x³3)、两条直线y =1和y =-1围成
的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而
成的几何体为W,过(0,y)(| y|£1)作W的水平截面,所得
截面面积为4p 1- y2 +8p,试利用祖暅原理、一个平放
的圆柱和一个长方体,得出W的体积值为__________
【解答】根据提示,一个半径为1,高为2p的圆柱平放,
一个高为2,底面面积8p的长方体,这两个几何体与W放
在一起,根据祖暅原理,每个平行水平面的截面面积都相等,故它们的体积相等,即W的
体积值为p×12×2p+2×8p=2p2 +16p.
14.对区间I上有定义的函数g(x),记g(I)={y| y = g(x),xÎI},已知定义域为[0,3]的
函数y = f(x)有反函数y = f -1(x),且 f -1([0,1))=[1,2), f -1((2,4])=[0,1),若方程
f(x)-x=0有解x ,则x = _____
0 0
【解答】根据反函数定义,当xÎ[0,1)时, f(x)Î(2,4];xÎ[1,2)时, f(x)Î[0,1),
而y = f(x)的定义域为[0,3],故当xÎ[2,3]时, f(x)的取值应在集合
(-¥,0)È[1,2]È(4,+¥),故若 f(x )= x ,只有x =2.
0 0 0
二、选择题
15.设常数aÎR,集合A={x|(x-1)(x-a)³0},B={x|x³a-1},若AÈB= R,
则a的取值范围为( )
(A) (-¥,2) (B) (-¥,2] (C) (2,+¥) (D) [2,+¥)
ì a³1 ì a£1
【解答】集合A讨论后利用数轴可知,í 或í ,解答选项为B.
îa-1£1 îa-1£a
16.钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的()
(A)充分条件 (B)必要条件 (C)充分必要条件 (D)既非充分也非必要条件
【解答】根据等价命题,便宜Þ没好货,等价于,好货Þ不便宜,故选B.
17.在数列{a }中,a =2n -1,若一个7行12列的矩阵的第i行第j列的元素
n n
a =a ×a +a +a ,(i =1,2, ,7; j =1,2, ,12)则该矩阵元素能取到的不同数值的
i,j i j i j L L
个数为( )
第2页 | 共8页(A)18 (B)28 (C)48 (D)63
【解答】a =a ×a +a +a =2i+j -1,而i+ j =2,3, ,19,故不同数值个数为18个,
i,j i j i j L
选A.
18.在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为
ur uur uur uur uur uur uur uur uur uur
a ,a ,a ,a ,a ;以D为起点,其余顶点为终点的向量分别为d ,d ,d ,d ,d .若m,M 分
1 2 3 4 5 1 2 3 4 5
ur uur uur uur uur uur
别为(a +a +a )×(d +d +d )的最小值、最大值,其中{i, j,k}Í{1,2,3,4,5},
i j k r s t
{r,s,t}Í{1,2,3,4,5},则m,M 满足( ).
(A) m=0,M >0 (B) m<0,M >0 (C) m<0,M =0 (D)
m<0,M <0
uuur uuur uuur uuur ur uur
【解答】作图知,只有AF×DE = AB×DC >0,其余均有a ×d £0,故选D.
i r
三、解答题
19.(本题满分12分)如图,在长方体ABCD-
A B C D 中,AB=2,AD=1,A A=1,证明直线BC 平行于平面DA C,并
1 1 1 1 1 1 1
D
求直线BC 到平面D AC的距离. C
1 1
A
【解答】因为ABCD-A B C D 为长方体,故AB//C D,AB=C D , B
1 1 1 1 1 1 1 1
故ABC D 为平行四边形,故BC // AD ,显然B不在平面D AC上,于 C
1 1 1 1 1 1
D
1
是直线BC 平行于平面DA C; A
1 1 1 B
1
直线BC 到平面D AC的距离即为点B到平面D AC的距离设为
1 1 1
h
1 1 1
考虑三棱锥ABCD 的体积,以ABC为底面,可得V = ´( ´1´2)´1=
1
3 2 3
3
而DADC中,AC = DC = 5,AD = 2 ,故S =
1 1 1 DAD 1 C 2
1 3 1 2 2
所以,V = ´ ´h= Þh= ,即直线BC 到平面D AC的距离为 .
1 1
3 2 3 3 3
20.(6分+8分)甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求
3
1£ x£10),每小时可获得利润是100(5x+1- )元.
x
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大
利润.
3 3
【解答】(1)根据题意,200(5x+1- )³3000Þ5x-14- ³0
x x
又1£ x£10,可解得3£ x£10
900 3 1 1 61
(2)设利润为y元,则y = ×100(5x+1- )=9´104[-3( - )2 + ]
x x x 6 12
故x=6时,y =457500元.
max
21.(6分+8分)已知函数 f(x)=2sin(wx),其中常数w>0;
p 2p
(1)若y = f(x)在[- , ]上单调递增,求w的取值范围;
4 3
第3页 | 共8页p
(2)令w=2,将函数y = f(x)的图像向左平移 个单位,再向上平移1个单位,得到函
6
数y = g(x)的图像,区间[a,b](a,bÎR且a0,根据题意有
ì p p
- w³-
ï ï 4 2 3
í Þ01,进而证明原点不是“C —C 型点”;
2 1 2
1
(3)求证:圆x2 + y2 = 内的点都不是“C —C 型点”.
1 2
2
2
【解答】:(1)C 的左焦点为F(- 3,0),过F的直线x=- 3与C 交于(- 3,± ),
1 1
2
与C 交于(- 3,±( 3+1)),故C 的左焦点为“C -C 型点”,且直线可以为x=- 3;
2 1 1 2
(2)直线y =kx与C 有交点,则
2
ì y =kx
í Þ(|k|-1)|x|=1,若方程组有解,则必须|k|>1;
î| y|=|x|+1
直线y =kx与C 有交点,则
2
ì y =kx 1
í Þ(1-2k2)x2 =2,若方程组有解,则必须k2 <
îx2 -2y2 =2 2
故直线y =kx至多与曲线C 和C 中的一条有交点,即原点不是“C -C 型点”。
1 2 1 2
1
(3)显然过圆x2 + y2 = 内一点的直线l若与曲线C 有交点,则斜率必存在;
1
2
根据对称性,不妨设直线l斜率存在且与曲线C 交于点(t,t+1)(t ³0),则
2
l: y =(t+1)=k(x-t)Þkx- y+(1+t-kt)=0
1 |1+t-kt| 2
直线l与圆x2 + y2 = 内部有交点,故 <
2 k2 +1 2
1
化简得,(1+t-tk)2 < (k2 +1)。。。。。。。。。。。。①
2
若直线l与曲线C 有交点,则
1
ìy =kx-kt+t+1
ï 1
í x2 Þ(k2 - )x2 +2k(1+t-kt)x+(1+t-kt)2 +1=0
- y2 =1 2
ï
î 2
1
D=4k2(1+t-kt)2 -4(k2 - )[(1+t-kt)2 +1]³0Þ(1+t-kt)2 ³2(k2 -1)
2
化简得,(1+t-kt)2 ³2(k2 -1)。。。。。②
1
由①②得,2(k2 -1)£(1+t-tk)2 < (k2 +1)Þk2 <1
2
1
但此时,因为t ³0,[1+t(1-k)]2 ³1, (k2 +1)<1,即①式不成立;
2
1
当k2 = 时,①式也不成立
2
第5页 | 共8页1
综上,直线l若与圆x2 + y2 = 内有交点,则不可能同时与曲线C 和C 有交点,
1 2
2
1
即圆x2 + y2 = 内的点都不是“C -C 型点” .
1 2
2
23.(3 分+6分+9分)给定常数c>0,定义函数 f(x)=2|x+c+4|-|x+c|,数列
a ,a ,a , 满足a = f(a ),nÎN*.
1 2 3 L n+1 n
(1)若a =-c-2,求a 及a ;(2)求证:对任意nÎN*,a -a ³c,;
1 2 3 n+1 n
(3)是否存在a ,使得a ,a , a , 成等差数列?若存在,求出所有这样的a ,若不存
1 1 2 L n L 1
在,说明理由.
【解答】:(1)因为c>0,a =-(c+2),故a = f(a )=2|a +c+4|-|a +c|=2
1 2 1 1 1
,
a = f(a )=2|a +c+4|-|a +c|=c+10
3 1 2 2
(2)要证明原命题,只需证明 f(x)³ x+c对任意xÎR都成立,
f(x)³ x+cÛ 2|x+c+4|-|x+c|³ x+c
即只需证明2|x+c+4|³|x+c|+x+c
若x+c£0,显然有2|x+c+4|³|x+c|+x+c=0成立;
若x+c>0,则2|x+c+4|³|x+c|+x+cÛ x+c+4> x+c显然成立
综上, f(x)³ x+c恒成立,即对任意的nÎN*,a -a ³c
n+1 n
(3)由(2)知,若{a }为等差数列,则公差d ³c>0,故n无限增大时,总有a >0
n n
此时,a = f(a )=2(a +c+4)-(a +c)=a +c+8
n+1 n n n n
即d =c+8
故a = f(a )=2|a +c+4|-|a +c|=a +c+8,
2 1 1 1 1
即2|a +c+4|=|a +c|+a +c+8,
1 1 1
当a +c³0时,等式成立,且n³2时,a >0,此时{a }为等差数列,满足题意;
1 n n
若a +c<0,则|a +c+4|=4Þa =-c-8,
1 1 1
此时,a =0,a =c+8, ,a =(n-2)(c+8)也满足题意;
2 3 L n
综上,满足题意的a 的取值范围是[-c,+¥)È{-c-8}.
1
22.(本题满分16分)本题共有3个小题.第1小题满分6分,第2小题满分5分,第3小题满
分8分.
x2
如图,已知双曲线C : - y2 =1,曲线C :| y|=|x|+1.P是平面内一点,若存
1 2 2
在过点P的直线与C 、C 都有公共点,则称P为“C - C 型点”.
1 2 1 2
(1)在正确证明C 的左焦点是“C - C 型点”时,要使
1 1 2
用一条过该焦点的直线,试写出一条这样的直线的方程(
不要求验证);
(2)设直线y =kx与C 有公共点,求证|k|>1,进而证
2
明原点不是“C - C 型点;
1 2
1
(3)求证:圆x2 + y2 = 内的点都不是“C - C 型点”
2 1 2
.
第6页 | 共8页2
22.解:(1)C 的左焦点为F(- 3,0),过F的直线x=- 3与C 交于(- 3,± ),与
1 1
2
C 交于(- 3,±( 3+1)),故C 的左焦点为“C -C 型点”,且直线可以为x=- 3;
2 1 1 2
(2)直线y =kx与C 有交点,则
2
ì y =kx
í Þ(|k|-1)|x|=1,若方程组有解,则必须|k|>1;
î| y|=|x|+1
直线y =kx与C 有交点,则
2
ì y =kx 1
í Þ(1-2k2)x2 =2,若方程组有解,则必须k2 <
îx2 -2y2 =2 2
故直线y =kx至多与曲线C 和C 中的一条有交点,即原点不是“C -C 型点”。
1 2 1 2
1
(3)显然过圆x2 + y2 = 内一点的直线l若与曲线C 有交点,则斜率必存在;
1
2
根据对称性,不妨设直线l斜率存在且与曲线C 交于点(t,t+1)(t ³0),则
2
l: y =(t+1)=k(x-t)Þkx- y+(1+t-kt)=0
1 |1+t-kt| 2
直线l与圆x2 + y2 = 内部有交点,故 <
2 k2 +1 2
1
化简得,(1+t-tk)2 < (k2 +1)。。。。。。。。。。。。①
2
若直线l与曲线C 有交点,则
1
ìy =kx-kt+t+1
ï 1
í x2 Þ(k2 - )x2 +2k(1+t-kt)x+(1+t-kt)2 +1=0
- y2 =1 2
ï
î 2
1
D=4k2(1+t-kt)2 -4(k2 - )[(1+t-kt)2 +1]³0Þ(1+t-kt)2 ³2(k2 -1)
2
化简得,(1+t-kt)2 ³2(k2 -1)。。。。。②
1
由①②得,2(k2 -1)£(1+t-tk)2 < (k2 +1)Þk2 <1
2
1
但此时,因为t ³0,[1+t(1-k)]2 ³1, (k2 +1)<1,即①式不成立;
2
1
当k2 = 时,①式也不成立
2
1
综上,直线l若与圆x2 + y2 = 内有交点,则不可能同时与曲线C 和C 有交点,
1 2
2
1
即圆x2 + y2 = 内的点都不是“C -C 型点”。
1 2
2
23.(本题满分18分)本题共有3个小题.第1小题满分3分,第2小题满分6分,第3小题满
分9分.
给定常数c>0,定义函数 f(x)=2|x+c+4|-|x+c|.数列a ,a ,a ,…满足
1 2 3
a = f(a ),nÎN*.
n+1 n
(1)若a =-c-2,求a 及a ;
1 2 3
(2)求证:对任意nÎN*,a -a ³c;
n+1 n
第7页 | 共8页(3)是否存在a ,使得a ,a ,a ,…,a …成等差数列?若存在,求出所有这样的
1 1 2 3 n
a ;若不存在,说明理由.
1
23.解:(1)因为c>0,a =-(c+2),故a = f(a )=2|a +c+4|-|a +c|=2,
1 2 1 1 1
a = f(a )=2|a +c+4|-|a +c|=c+10
3 1 2 2
(2)要证明原命题,只需证明 f(x)³ x+c对任意xÎR都成立,
f(x)³ x+cÛ 2|x+c+4|-|x+c|³ x+c
即只需证明2|x+c+4|³|x+c|+x+c
若x+c£0,显然有2|x+c+4|³|x+c|+x+c=0成立;
若x+c>0,则2|x+c+4|³|x+c|+x+cÛ x+c+4> x+c显然成立
综上, f(x)³ x+c恒成立,即对任意的nÎN*,a -a ³c
n+1 n
(3)由(2)知,若{a }为等差数列,则公差d ³c>0,故n无限增大时,总有a >0
n n
此时,a = f(a )=2(a +c+4)-(a +c)=a +c+8
n+1 n n n n
即d =c+8
故a = f(a )=2|a +c+4|-|a +c|=a +c+8,
2 1 1 1 1
即2|a +c+4|=|a +c|+a +c+8,
1 1 1
当a +c³0时,等式成立,且n³2时,a >0,此时{a }为等差数列,满足题意;
1 n n
若a +c<0,则|a +c+4|=4Þa =-c-8,
1 1 1
此时,a =0,a =c+8, ,a =(n-2)(c+8)也满足题意;
2 3 L n
综上,满足题意的a 的取值范围是[-c,+¥)È{-c-8}。
1
第8页 | 共8页