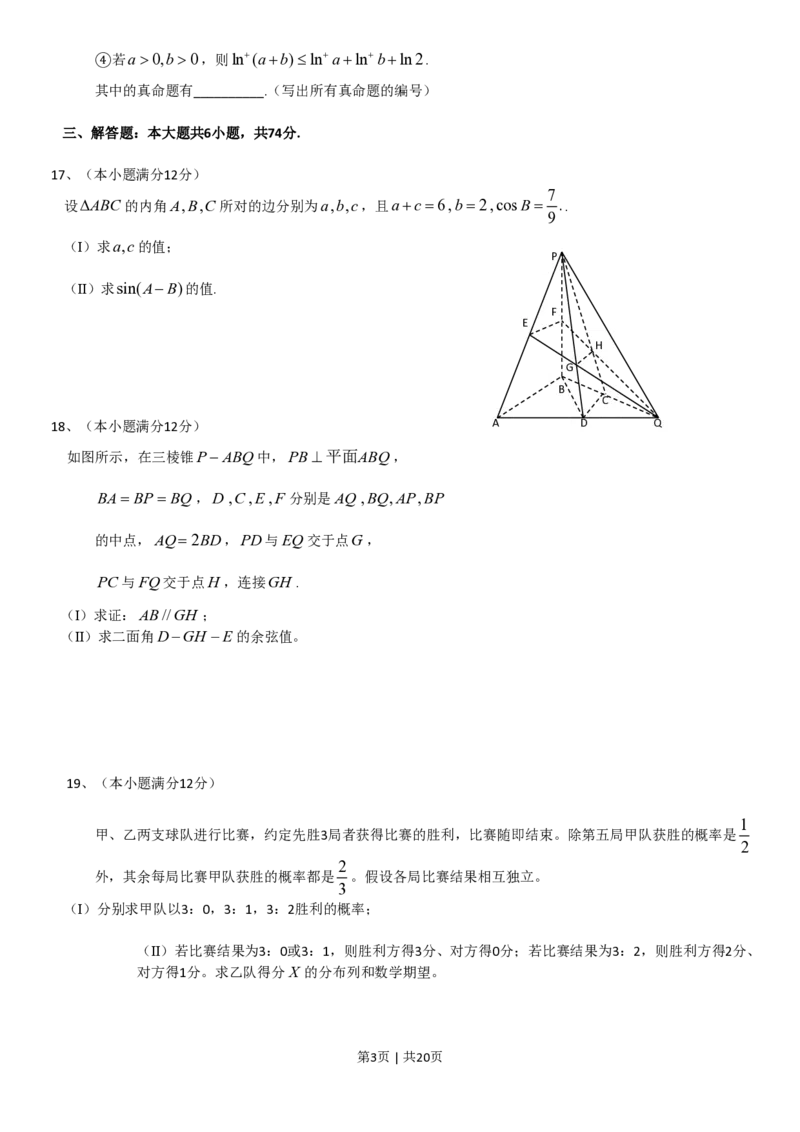文档内容
2013年普通高等学校招生全国统一考试(山东卷) 理 科 数 学
P(AB)= P(A)·P(B)
参考公式:如果事件A、B互斥,那么P(A+B)= P(A)+P(B) 如果事件A、B独立,那么 。
第Ⅰ卷(共60分)
一、选择题:本大题共12小题。每小题5分共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、复数z满组(z-3)(2-i)=5(z为虚数单位),则z的共轭复数z为
(A) 2+i (B) 2-i (C) 5+i (D) 5-i
2、已知集合A=0,1,2,则集合B= x- y xÎA,yÎA 中元素的个数是
(A) 1 (B) 3 (C) 5 (D) 9
1
3、已知函数 f(x)为奇函数,且当x>0时, f(x)= x2 + ,则 f(-1)=
x
(A) -2 (B) 0 (C) 1 (D) 2
9
4、已知三棱柱ABC-ABC 的侧棱与底面垂直,体积为 ,底面是边长为 3的正三角形,若P为底面
1 1 1 4
ABC 的中心,则PA与平面ABC所成角的大小为
1 1 1
5p p p p
(A) (B) (C) (D)
12 3 4 6
p
5、将函数y =sin(2x+j)的图象沿x轴向左平移 个单位后,得到一个偶函数的图象,则j的一个可能取值
8
为
3p p p
(A) (B) (C) 0 (D) -
4 4 4
ì2x- y-2³0,
ï
6、在平面直角坐标系xOy中,M 为不等式组íx+2y-1³0, 所表示的区域上一动点,则直线OM
ï
3x+ y-8£0
î
的斜率的最小值为
1 1
(A) 2 (B) 1 (C) - (D) -
3 2
7、给定两个命题 p,q. 若Øp是q的必要不充分条件,则 p是Øq的
(A) 充分不必要条件 (B) 必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件
8、函数y = xcosx+sinx的图象大致为
y y y y
p p p p
O x O x O x O x
第1页 | 共20页(A) (B) (C) (D)
9、过点(3,1)作圆(x-1)2 + y2 =1的两条切线,切点分别为A,B,则直线AB的方程为
(A) 2x+ y-3=0 (B) 2x- y-3=0 (C) 4x- y-3=0 (D) 4x+ y-3=0
10、用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为
(A) 243 (B) 252 (C) 261 (D) 279
1 x2
11、抛物线C : y = x2(p>0)的焦点与双曲线C : - y2 =1的右焦点的连线交C 于第一象限的点M. 若
1 2p 2 3 1
C 在点M 处的切线平行于C 的一条渐近线,则 p=
1 2
3 3 2 3 4 3
(A) (B) (C) (D)
16 8 3 3
xy 2 1 2
12、设正实数x,y,z满足x2 -3xy+4y2 -z =0.则当 取得最大值时, + - 的最大值为
z x y z
9 开 始
(A) 0 (B) 1 (C) (D) 3
4
第Ⅱ卷(共90分) 输入e(e>0)
二、填空题:本大题共4小题,每小题4分,共16分。
F =1,F = 2,n =1
13、执行右图所示的程序框图,若输入c的值为0.25,
0 1
则输出的n的值为_______.
14、在区间[-3,3] 上随机取一个数x,
F = F + F
1 0 1
使得 x+1+ x-2 ³1成立的概率为______.
uuur uuur F = F + F
15、已知向量AB与AC的夹角为1200, 0 1 0
uuur uuur uuur uuur uuur
且AB=3,AC =2.若AP=lAB+ AC,
n = n+1
uuur uuur
且AP^ BC,则实数l的值为____________.
ì0, 0< x<1, 否
16、定义“正对数”:ln+ x=í 现有四个命题: 1
îlnx, x³1. £e
F
1
①若a>0,b>0,则ln+(ab)=bln+ a;
是
②若a>0,b>0,则ln+(ab)=ln+ a+ln+b;
n
输出
a
③若a>0,b>0,则ln+( )³ln+ a-ln+b;
b
第2页 | 共20页
结 束④若a>0,b>0,则ln+(a+b)£ln+ a+ln+b+ln2.
其中的真命题有__________.(写出所有真命题的编号)
三、解答题:本大题共6小题,共74分.
17、(本小题满分12分)
7
设DABC 的内角A,B,C 所对的边分别为a,b,c,且a+c=6,b=2,cosB= ..
9
(Ⅰ)求a,c的值;
P
(Ⅱ)求sin(A-B)的值.
F
E
H
G
B
C
18、(本小题满分12分) A D Q
如图所示,在三棱锥P-ABQ中,PB^平面ABQ,
BA= BP= BQ,D ,C,E,F 分别是AQ ,BQ,AP,BP
的中点,AQ=2BD,PD与EQ交于点G,
PC与FQ交于点H ,连接GH .
(Ⅰ)求证:AB//GH ;
(Ⅱ)求二面角D-GH -E的余弦值。
19、(本小题满分12分)
1
甲、乙两支球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
2
2
外,其余每局比赛甲队获胜的概率都是 。假设各局比赛结果相互独立。
3
(Ⅰ)分别求甲队以3:0,3:1,3:2胜利的概率;
(Ⅱ)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、
对方得1分。求乙队得分X 的分布列和数学期望。
第3页 | 共20页20、(本小题满分12分)
设等差数列a 的前n项和为S ,且S =4S ,a =2a +1.
n n 4 2 2n n
(Ⅰ)求数列{a }的通项公式;
n
a +1
(Ⅱ)设数列{b }的前n项和为T ,且T + n =l(l为常数)。令c =2b ,(nÎN*),求数
n n n 2n n 2n
列{c }的前n项和R 。
n n
21、(本小题满分13分)
x
设函数 f(x)= +c(e=2.71828… 是自然对数的底数,cÎR)
e2x
(Ⅰ)求 f(x)的单调区间、最大值;
(Ⅱ)讨论关于x的方程 lnx = f(x)根的个数。
22、(本小题满分13分)
x2 y2 3
椭圆C: + =1(a>b>0)的左、右焦点分别是F ,F ,离心率为 ,过F 且垂直于x轴
a2 b2 1 2 2 1
的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF ,PF 。设ÐFPF 的角平分线PM 交C
1 2 1 2
的长轴于点M(m,0),求m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点。设直线
第4页 | 共20页1 1
PF ,PF 的斜率分别为k ,k ,若k ¹0,试证明 + 为定值,并求出这个定值.
1 2 1 2 kk kk
1 2
一、选择题
1.(5分)(2013•山东)复数z满足(z﹣3)(2﹣i)=5(i为虚数单位),则z的共轭复数 为( )
A.2+i B.2﹣i C.5+i D.5﹣i
考点: 复数的基本概念.
3253948
专题: 计算题.
分析: 利用复数的运算法则求得z,即可求得z的共轭复数 .
解答: 解:∵(z﹣3)(2﹣i)=5,
∴z﹣3= =2+i
∴z=5+i,
∴ =5﹣i.
故选D.
点评: 本题考查复数的基本概念与基本运算,求得复数z是关键,属于基础题.
2.(5分)(2013•山东)已知集合A={0,1,2},则集合B={x﹣y|x∈A,y∈A}中元素的个数是( )
A.1 B.3 C.5 D.9
考点: 集合中元素个数的最值.
3253948
专题: 计算题.
分析: 依题意,可求得集合B={﹣2,﹣1,0,1,2},从而可得答案.
解答: 解:∵A={0,1,2},B={x﹣y|x∈A,y∈A},
∴当x=0,y分别取0,1,2时,x﹣y的值分别为0,﹣1,﹣2;
当x=1,y分别取0,1,2时,x﹣y的值分别为1,0,﹣1;
当x=2,y分别取0,1,2时,x﹣y的值分别为2,1,0;
∴B={﹣2,﹣1,0,1,2},
∴集合B={x﹣y|x∈A,y∈A}中元素的个数是5个.
故选C.
点评: 本题考查集合中元素个数的最值,理解题意是关键,考查分析运算能力,属于中档题.
3.(5分)(2013•山东)已知函数f(x)为奇函数,且当x>0时, ,则f(﹣1)=( )
A.﹣2 B.0 C.1 D.2
考点: 函数的值.
3253948
专题: 计算题;函数的性质及应用.
分析: 利用奇函数的性质,f(﹣1)=﹣f(1),即可求得答案.
解答:
解:∵函数f(x)为奇函数,x>0时,f(x)=x2+ ,
∴f(﹣1)=﹣f(1)=﹣2,
第5页 | 共20页故选A.
点评: 本题考查奇函数的性质,考查函数的求值,属于基础题.
4.(5分)(2013•山东)已知三棱柱ABC﹣A BC的侧棱与底面垂直,体积为 ,底面是边长为 的正三角形,若P为
1 1 1
底面ABC的中心,则PA与平面ABC所成角的大小为( )
1 1 1
A. B. C. D.
考点: 直线与平面所成的角.
3253948
专题: 空间角.
分析: 利用三棱柱ABC﹣ABC的侧棱与底面垂直和线面角的定义可知,∠APA为PA与平面ABC所成角,即为∠AP
1 1 1 1 1 1 1
A为PA与平面ABC所成角.利用三棱锥的体积计算公式可得AA,再利用正三角形的性质可得AP,在Rt△AA
1 1 1 1
P中,利用tan∠APA= 即可得出.
1
解答: 解:如图所示,
∵AA⊥底面ABC,∴∠APA为PA与平面ABC所成角,
1 1 1 1 1 1 1 1
∵平面ABC∥平面ABC,∴∠APA为PA与平面ABC所成角.
1 1 1 1
∵ = = .
∴V = = ,解得 .
三棱柱ABC﹣A1B1C1
又P为底面正三角形ABC的中心,∴ = =1,
1 1 1
在Rt△AAP中, ,
1
∴ .
故选B.
点评: 熟练掌握三棱柱的性质、体积计算公式、正三角形的性质、线面角的定义是解题的关键.
5.(5分)(2013•山东)函数y=sin(2x+φ)的图象沿x轴向左平移 个单位后,得到一个偶函数的图象,则φ的一
个可能的值为( )
第6页 | 共20页A. B. C.0 D.
考点: 函数y=Asin(ωx+φ)的图象变换.
3253948
专题: 计算题;三角函数的图像与性质.
分析:
利用函数y=Asin(ωx+φ)的图象变换可得函数y=sin(2x+φ)的图象沿x轴向左平移 个单位后的解析
式,利用其为偶函数即可求得答案.
解答: 解:令y=f(x)=sin(2x+φ),
则f(x+ )=sin[2(x+ )+φ]=sin(2x+ +φ),
∵f(x+ )为偶函数,
∴ +φ=kπ+ ,
∴φ=kπ+ ,k∈Z,
∴当k=0时,φ= .
故φ的一个可能的值为 .
故选B.
点评: 本题考查函数y=Asin(ωx+φ)的图象变换,考查三角函数的奇偶性,属于中档题.
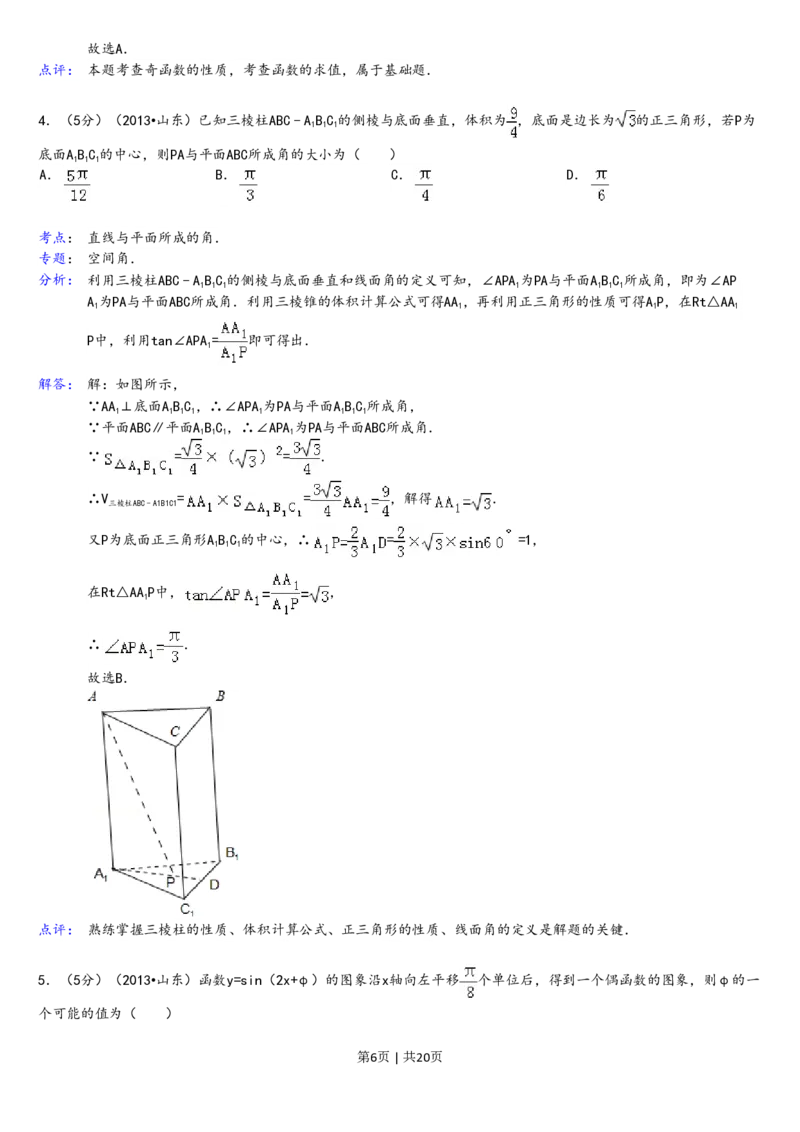
6.(5分)(2013•山东)在平面直角坐标系xOy中,M为不等式组 所表示的区域上一动点,则直线OM
斜率的最小值为( )
A.2 B.1 C. D.
考点: 简单线性规划.
3253948
专题: 不等式的解法及应用.
分析: 本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与原点(0
,0)构成的直线的斜率的最小值即可.
解答:
解:不等式组 表示的区域如图,
当M取得点A(3,﹣1)时,
z直线OM斜率取得最小,最小值为
k= =﹣ .
故选C.
第7页 | 共20页点评: 本题利用直线斜率的几何意义,求可行域中的点与原点的斜率.本题主要考查了用平面区域二元一次不等
式组,以及简单的转化思想和数形结合的思想,属中档题.
7.(5分)(2013•山东)给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
考点: 必要条件、充分条件与充要条件的判断.
3253948
专题: 规律型.
分析: 根据互为逆否命题真假性相同,可将已知转化为q是¬p的充分不必要条件,进而根据逆否命题及充要条件
的定义得到答案.
解答: 解:∵¬p是q的必要而不充分条件,
∴q是¬p的充分不必要条件,即q⇒¬p,但¬p不能⇒q,
其逆否命题为p⇒¬q,但¬q不能⇒p,
则p是¬q的充分不必要条件.
故选A.
点评: 本题考查的知识点是充要条件的判断,其中将已知利用互为逆否命题真假性相同,转化为q是¬p的充分不
必要条件,是解答的关键.
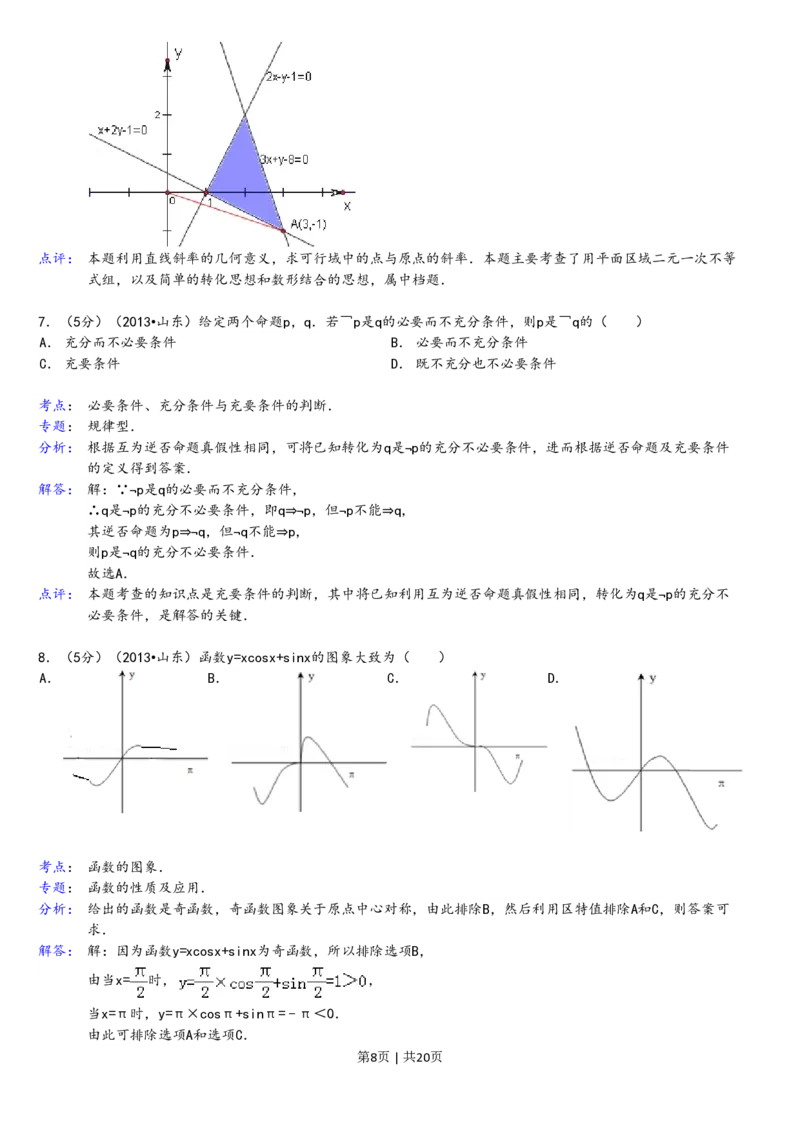
8.(5分)(2013•山东)函数y=xcosx+sinx的图象大致为( )
A. B. C. D.
考点: 函数的图象.
3253948
专题: 函数的性质及应用.
分析: 给出的函数是奇函数,奇函数图象关于原点中心对称,由此排除B,然后利用区特值排除A和C,则答案可
求.
解答: 解:因为函数y=xcosx+sinx为奇函数,所以排除选项B,
由当x= 时, ,
当x=π时,y=π×cosπ+sinπ=﹣π<0.
由此可排除选项A和选项C.
第8页 | 共20页故正确的选项为D.
故选D.
点评: 本题考查了函数的图象,考查了函数的性质,考查了函数的值,是基础题.
9.(5分)(2013•山东)过点(3,1)作圆(x﹣1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为(
)
A.2x+y﹣3=0 B.2x﹣y﹣3=0 C.4x﹣y﹣3=0 D.4x+y﹣3=0
考点: 圆的切线方程;直线的一般式方程.
3253948
专题: 计算题;直线与圆.
分析: 由题意判断出切点(1,1)代入选项排除B、D,推出令一个切点判断切线斜率,得到选项即可.
解答: 解:因为过点(3,1)作圆(x﹣1)2+y2=1的两条切线,切点分别为A,B,
所以圆的一条切线方程为y=1,切点之一为(1,1),显然B、D选项不过(1,1),B、D不满足题意;
另一个切点的坐标在(1,﹣1)的右侧,所以切线的斜率为负,选项C不满足,A满足.
故选A.
点评: 本题考查直线与圆的位置关系,圆的切线方程求法,可以直接解答,本题的解答是间接法,值得同学学习
.
10.(5分)(2013•山东)用0,1,2,…,9十个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252 C.261 D.279
考点: 排列、组合及简单计数问题.
3253948
专题: 计算题.
分析: 求出所有三位数的个数,减去没有重复数字的三位数个数即可.
解答: 解:用0,1,2,…,9十个数字,所有三位数个数为:900,
其中没有重复数字的三位数百位数从非0的9个数字中选取一位,十位数从余下的9个数字中选一个,个位
数再从余下的8个中选一个,所以共有:9×9×8=648,
所以可以组成有重复数字的三位数的个数为:900﹣648=252.
故选B.
点评: 本题考查排列组合以及简单计数原理的应用,利用间接法求解是解题的关键,考查计算能力.
11.(5分)(2013•山东)抛物线C : 的焦点与双曲线C: 的右焦点的连线交C 于第一
1 2 1
象限的点M.若C在点M处的切线平行于C 的一条渐近线,则p=( )
1 2
A. B. C. D.
考点: 利用导数研究曲线上某点切线方程;双曲线的简单性质.
3253948
专题: 压轴题;圆锥曲线的定义、性质与方程.
分析: 由曲线方程求出抛物线与双曲线的焦点坐标,由两点式写出过两个焦点的直线方程,求出函数
在x取直线与抛物线交点M的横坐标时的导数值,由其等于双曲线渐近线的斜率得到交
点横坐标与p的关系,把M点的坐标代入直线方程即可求得p的值.
解答:
解:由 ,得x2=2py(p>0),
所以抛物线的焦点坐标为F( ).
第9页 | 共20页由 ,得 , .
所以双曲线的右焦点为(2,0).
则抛物线的焦点与双曲线的右焦点的连线所在直线方程为 ,
即 ①.
设该直线交抛物线于M( ),则C在点M处的切线的斜率为 .
1
由题意可知 ,得 ,代入M点得M( )
把M点代入①得: .
解得p= .
故选D.
点评: 本题考查了双曲线的简单几何性质,考查了利用导数研究曲线上某点的切线方程,函数在曲线上某点处的
切线的斜率等于函数在该点处的导数,是中档题.
12.(5分)(2013•山东)设正实数x,y,z满足x2﹣3xy+4y2﹣z=0.则当 取得最大值时, 的最大值为(
)
A.0 B.1 C. D.3
考点: 基本不等式.
3253948
专题: 计算题;压轴题;不等式的解法及应用.
分析:
依题意,当 取得最大值时x=2y,代入所求关系式f(y)= + ﹣ ,利用配方法即可求得其最大值.
解答: 解:∵x2﹣3xy+4y2﹣z=0,
∴z=x2﹣3xy+4y2,又x,y,z均为正实数,
∴ = = ≤ =1(当且仅当x=2y时取“=”),
∴ =1,此时,x=2y.
∴z=x2﹣3xy+4y2=(2y)2﹣3×2y×y+4y2=2y2,
∴ + ﹣ = + ﹣ =﹣ +1≤1.
∴ 的最大值为1.
故选B.
第10页 | 共20页点评:
本题考查基本不等式,由 取得最大值时得到x=2y是关键,考查配方法求最值,属于中档题.
二、填空题
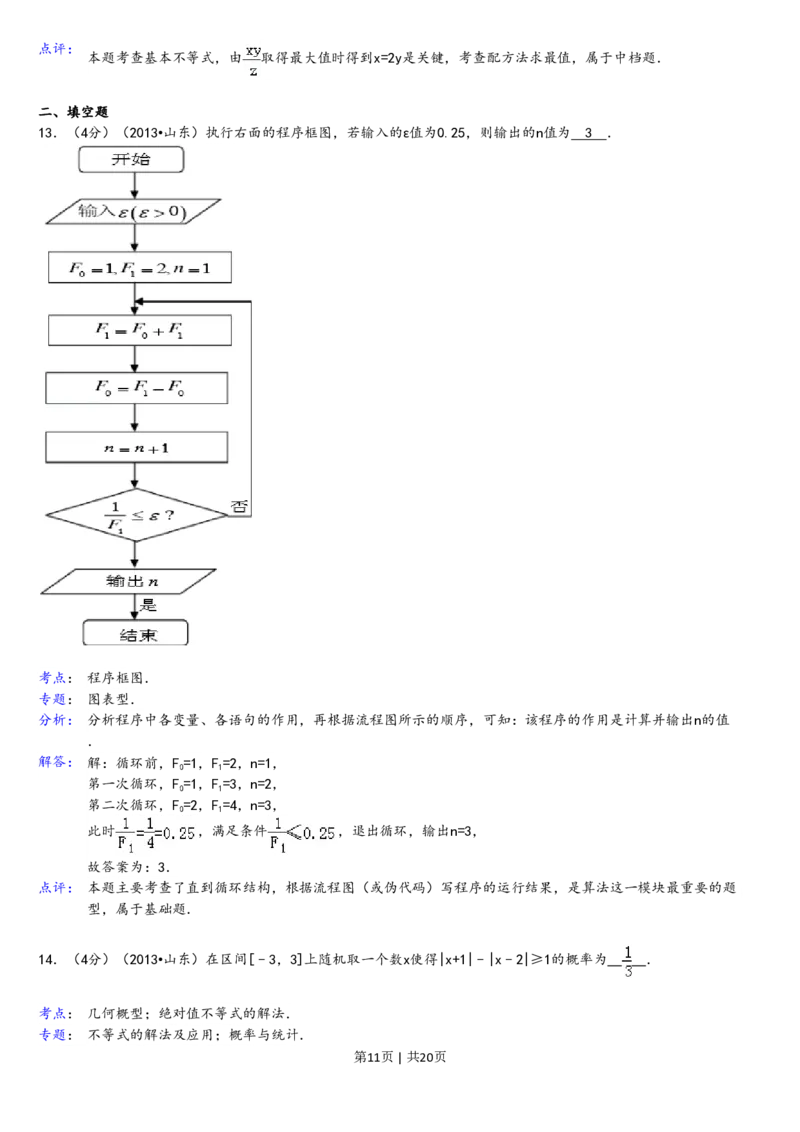
13.(4分)(2013•山东)执行右面的程序框图,若输入的ɛ值为0.25,则输出的n值为 3 .
考点: 程序框图.
3253948
专题: 图表型.
分析: 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出n的值
.
解答: 解:循环前,F=1,F=2,n=1,
0 1
第一次循环,F=1,F=3,n=2,
0 1
第二次循环,F=2,F=4,n=3,
0 1
此时 ,满足条件 ,退出循环,输出n=3,
故答案为:3.
点评: 本题主要考查了直到循环结构,根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题
型,属于基础题.
14.(4分)(2013•山东)在区间[﹣3,3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为 .
考点: 几何概型;绝对值不等式的解法.
3253948
专题: 不等式的解法及应用;概率与统计.
第11页 | 共20页分析: 本题利用几何概型求概率.先解绝对值不等式,再利用解得的区间长度与区间[﹣3,3]的长度求比值即得
.
解答: 解:利用几何概型,其测度为线段的长度.
由不等式|x+1|﹣|x﹣2|≥1 可得 ① ,或② ,
③ .
解①可得x∈∅,解②可得1≤x<2,解③可得 x≥2.
故原不等式的解集为{x|x≥1},
∴|在区间[﹣3,3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为P= = .
故答案为:
点评: 本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积
)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.
15.(4分)(2013•山东)已知向量 与 的夹角为120°,且 , .若 ,且
,则实数λ= .
考点: 数量积表示两个向量的夹角;向量的模.
3253948
专题: 计算题;压轴题;平面向量及应用.
分析:
利用 , ,表示 向量,通过数量积为0,求出λ的值即可.
解答:
解:由题意可知: ,
因为 ,
所以 ,
所以
=
=
=﹣12λ+7=0
解得λ= .
故答案为: .
点评: 本题考查向量的数量积的应用,向量的垂直,考查转化数学与计算能力.
16.(4分)(2013•山东)定义“正数对”:ln+x= ,现有四个命题:
第12页 | 共20页①若a>0,b>0,则ln+(ab)=bln+a;
②若a>0,b>0,则ln+(ab)=ln+a+ln+b;
③若a>0,b>0,则 ;
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+2.
其中的真命题有 ①③④ (写出所有真命题的序号)
考点: 命题的真假判断与应用.
3253948
专题: 综合题;压轴题;新定义.
分析: 由题意,根据所给的定义及对数的运算性质对四个命题进行判断,由于在不同的定义域中函数的解析式不
一样,故需要对a,b分类讨论,判断出每个命题的真假
解答: 解:对于①,由定义,当a≥1时,ab≥1,故ln+(ab)=ln(ab)=blna,又bln+a=blna,故有ln+(ab)=bln+
a;
当a<1时,ab<1,故ln+(ab)=0,又a<1时bln+a=0,所以此时亦有ln+(ab)=bln+a.由上判断知①正确
;
对于②,此命题不成立,可令a=2,b= ,则ab= ,由定义ln+(ab)=0,ln+a+ln+b=ln2,所以ln+(ab)≠
ln+a+ln+b;由此知②错误;
对于③,当a≥b>0时, ≥1,此时 ≥0,当a≥b≥1时,ln+a﹣ln+b=lna﹣lnb=
,此时命题成立;当a>1>b时,ln+a﹣ln+b=lna,此时 ,故命题成立;同理可验证当1>a
≥b>0时, 成立;当 <1时,同理可验证是正确的,故③正确;
对于④,可分a≤1,b≤1与两者中仅有一个小于等于1、两者都大于1三类讨论,依据定义判断出④是正确
的
故答案为①③④
点评: 本题考查新定义及对数的运算性质,理解定义所给的运算规则是解题的关键,本题考查了分类讨论的思想
,逻辑判断的能力,综合性较强,探究性强.易因为理解不清定义及忘记分类讨论的方法解题导致无法入
手致错
三、解答题
17.(12分)(2013•山东)设△ABC的内角A,B,C所对边分别为a,b,c,且a+c=6,b=2, .
(1)求a,c的值;
(2)求sin(A﹣B)的值.
考点: 余弦定理;同角三角函数间的基本关系;两角和与差的正弦函数;正弦定理.
3253948
专题: 解三角形.
分析: (1)利用余弦定理列出关于新,将b与cosB的值代入,利用完全平方公式变形,求出acb的值,与a+c的值
联立即可求出a与c的值即可;
(2)先由cosB的值,利用同角三角函数间的基本关系求出sinB的值,再由a,b及sinB的值,利用正弦定
理求出sinA的值,进而求出cosA的值,所求式子利用两角和与差的正弦函数公式化简后,将各自的值代入
计算即可求出值.
解答:
解:(1)∵a+c=6①,b=2,cosB= ,
∴由余弦定理得:b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣ ac=36﹣ ac=4,
第13页 | 共20页整理得:ac=9②,
联立①②解得:a=c=3;
(2)∵cosB= ,B为三角形的内角,
∴sinB= = ,
∵b=2,a=3,sinB= ,
∴由正弦定理得:sinA= = = ,
∵a=c,即A=C,∴A为锐角,
∴cosA= = ,
则sin(A﹣B)=sinAcosB﹣cosAsinB= × ﹣ × = .
点评: 此题考查了正弦、余弦定理,两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握定
理及公式是解本题的关键.
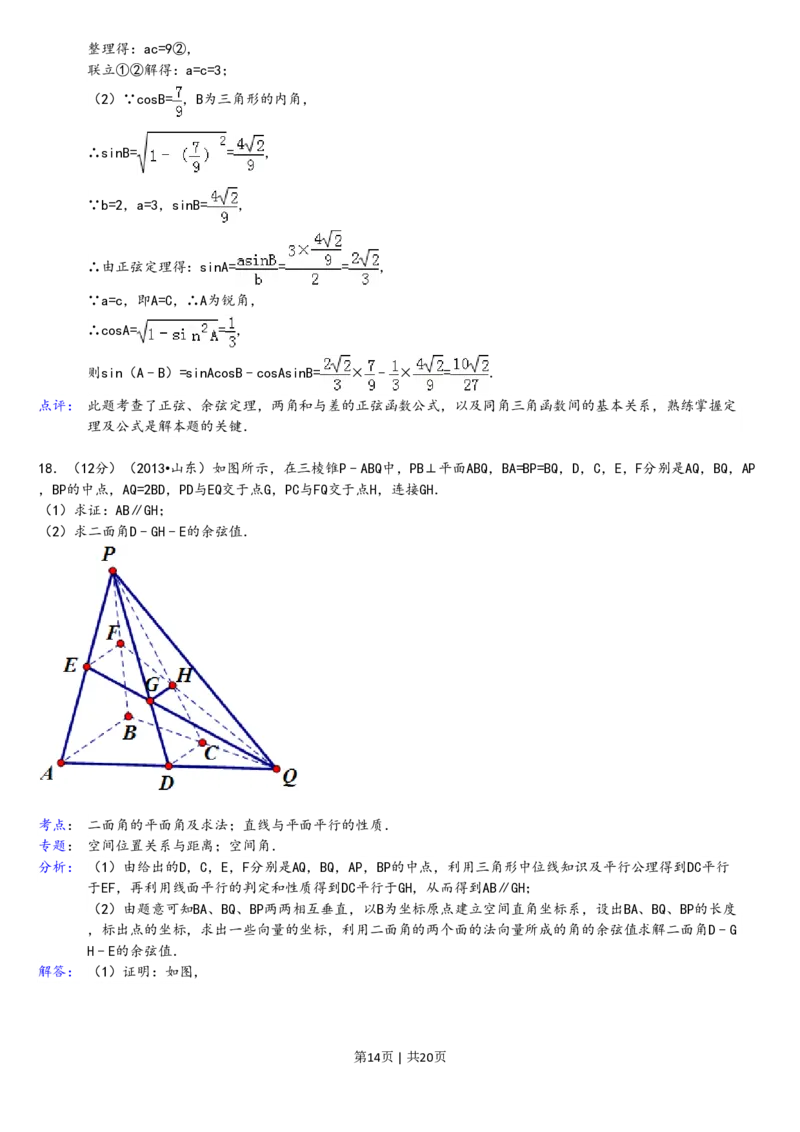
18.(12分)(2013•山东)如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP
,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值.
考点: 二面角的平面角及求法;直线与平面平行的性质.
3253948
专题: 空间位置关系与距离;空间角.
分析: (1)由给出的D,C,E,F分别是AQ,BQ,AP,BP的中点,利用三角形中位线知识及平行公理得到DC平行
于EF,再利用线面平行的判定和性质得到DC平行于GH,从而得到AB∥GH;
(2)由题意可知BA、BQ、BP两两相互垂直,以B为坐标原点建立空间直角坐标系,设出BA、BQ、BP的长度
,标出点的坐标,求出一些向量的坐标,利用二面角的两个面的法向量所成的角的余弦值求解二面角D﹣G
H﹣E的余弦值.
解答: (1)证明:如图,
第14页 | 共20页∵C,D为AQ,BQ的中点,∴CD∥AB,
又E,F分别AP,BP的中点,∴EF∥AB,
则EF∥CD.又EF⊂平面EFQ,∴CD∥平面EFQ.
又CD⊂平面PCD,且平面PCD∩平面EFQ=GH,∴CD∥GH.
又AB∥CD,∴AB∥GH;
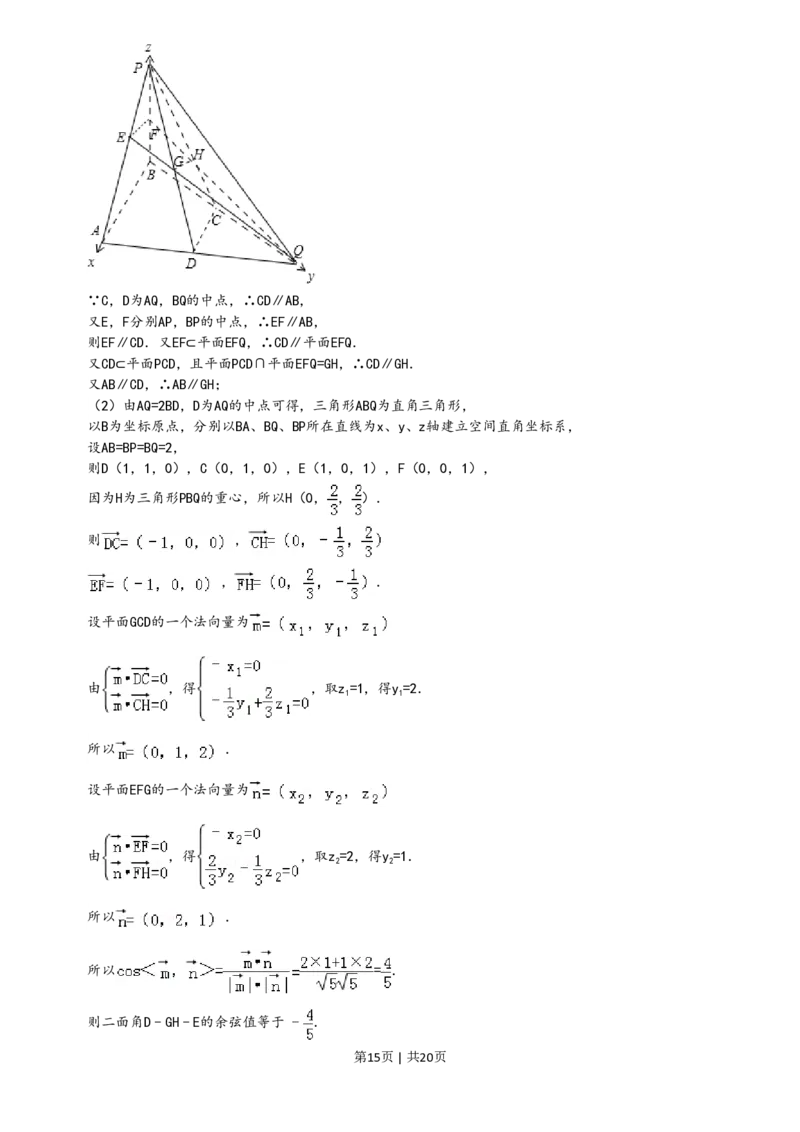
(2)由AQ=2BD,D为AQ的中点可得,三角形ABQ为直角三角形,
以B为坐标原点,分别以BA、BQ、BP所在直线为x、y、z轴建立空间直角坐标系,
设AB=BP=BQ=2,
则D(1,1,0),C(0,1,0),E(1,0,1),F(0,0,1),
因为H为三角形PBQ的重心,所以H(0, , ).
则 ,
, .
设平面GCD的一个法向量为
由 ,得 ,取z=1,得y=2.
1 1
所以 .
设平面EFG的一个法向量为
由 ,得 ,取z=2,得y=1.
2 2
所以 .
所以 = .
则二面角D﹣GH﹣E的余弦值等于 .
第15页 | 共20页点评: 本题考查了直线与平面平行的性质,考查了二面角的平面角及其求法,考查了学生的空间想象能力和思维
能力,考查了计算能力,解答此题的关键是正确求出H点的坐标,是中档题.
19.(12分)(2013•山东)甲乙两支排球队进行比赛,先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获
胜的概率是 ,其余每局比赛甲队获胜的概率都是 .设各局比赛结果相互独立.
(1)分别求甲队3:0,3:1,3:2胜利的概率;
(2)若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙
队得分X的分布列及数学期望.
考点: 离散型随机变量的期望与方差.
3253948
专题: 概率与统计.
分析: (1)甲队获胜有三种情形,①3:0,②3:1,③3:2,其每种情形的最后一局肯定是甲队胜,分别求出
相应的概率,最后根据互斥事件的概率公式求出甲队获得这次比赛胜利的概率;
(2)X的取值可能为0,1,2,3,然后利用相互独立事件的概率乘法公式求出相应的概率,列出分布列,
最后根据数学期望公式解之即可.
解答: 解:(1)甲队获胜有三种情形,其每种情形的最后一局肯定是甲队胜
①3:0,概率为P=( )3= ;
1
②3:1,概率为P=C ( )2×(1﹣ )× = ;
2
③3:2,概率为P=C ( )2×(1﹣ )2× =
3
∴甲队3:0,3:1,3:2胜利的概率: .
(2)乙队得分X,则X的取值可能为0,1,2,3.
由(1)知P(X=0)=P+P= ;
1 2
P(X=1)=P= ;
3
P(X=2)=C (1﹣ )2×( )2× = ;
P(X=3)=(1﹣ )3+C (1﹣ )2×( )× = ;
则X的分布列为
X 3 2 1 0
P
E(X)=3× +2× +1× +0× = .
点评: 本题主要考查了相互独立事件的概率乘法公式,以及离散型随机变量的期望与分布列,同时考查了分类讨
论的数学思想,属于中档题.
20.(12分)(2013•山东)设等差数列{a }的前n项和为S,且S=4S,a =2a+1.
n n 4 2 2n n
(1)求数列{a}的通项公式;
n
(2)设数列{b}的前n项和为T 且 (λ为常数).令c=b (n∈N※)求数列{c}的前n项和R.
n n n 2n n n
第16页 | 共20页考点: 等差数列的通项公式;数列的求和.
3253948
专题: 等差数列与等比数列.
分析: (1)设出等差数列的首项和公差,由已知条件列关于首项和公差的方程组,解出首项和公差后可得数列{
a}的通项公式;
n
(2)把{a}的通项公式代入 ,求出当n≥2时的通项公式,然后由c=b 得数列{c}的通项公
n n 2n n
式,最后利用错位相减法求其前n项和.
解答: 解:(1)设等差数列{a}的首项为a,公差为d,由a =2a+1,取n=1,得a=2a+1,即a﹣d+1=0①
n 1 2n n 2 1 1
再由S=4S,得 ,即d=2a②
4 2 1
联立①、②得a=1,d=2.
1
所以a=a+(n﹣1)d=1+2(n﹣1)=2n﹣1;
n 1
(2)把a=2n﹣1代入 ,得 ,则 .
n
所以b=T=λ﹣1,
1 1
当n≥2时, = .
所以 , .
R=c+c+…+c= ③
n 1 2 n
④
③﹣④得: =
所以 ;
所以数列{c}的前n项和 .
n
点评: 本题考查了等差数列的通项公式,考查了数列的求和,训练了错位相减法,考查了学生的计算能力,属中
档题.
21.(13分)(2013•山东)设函数 .
(1)求f(x)的单调区间及最大值;
(2)讨论关于x的方程|lnx|=f(x)根的个数.
考点: 利用导数研究函数的单调性;根的存在性及根的个数判断.
3253948
专题: 压轴题;导数的综合应用.
第17页 | 共20页分析: (1)利用导数的运算法则求出f′(x),分别解出f′(x)>0与f′(x)<0即可得出单调区间及极值与最
值;
(2)分类讨论:①当0<x≤1时,令u(x)=﹣lnx﹣ ﹣c,②当x≥1时,令v(x)=lnx﹣ .利
用导数分别求出c的取值范围,即可得出结论.
解答:
解:(1)∵ = ,解f′(x)>0,得 ;解f′(x)<0,得 .
∴函数f(x)的单调递增区间为 ;单调递减区间为 .
故f(x)在x= 取得最大值,且 .
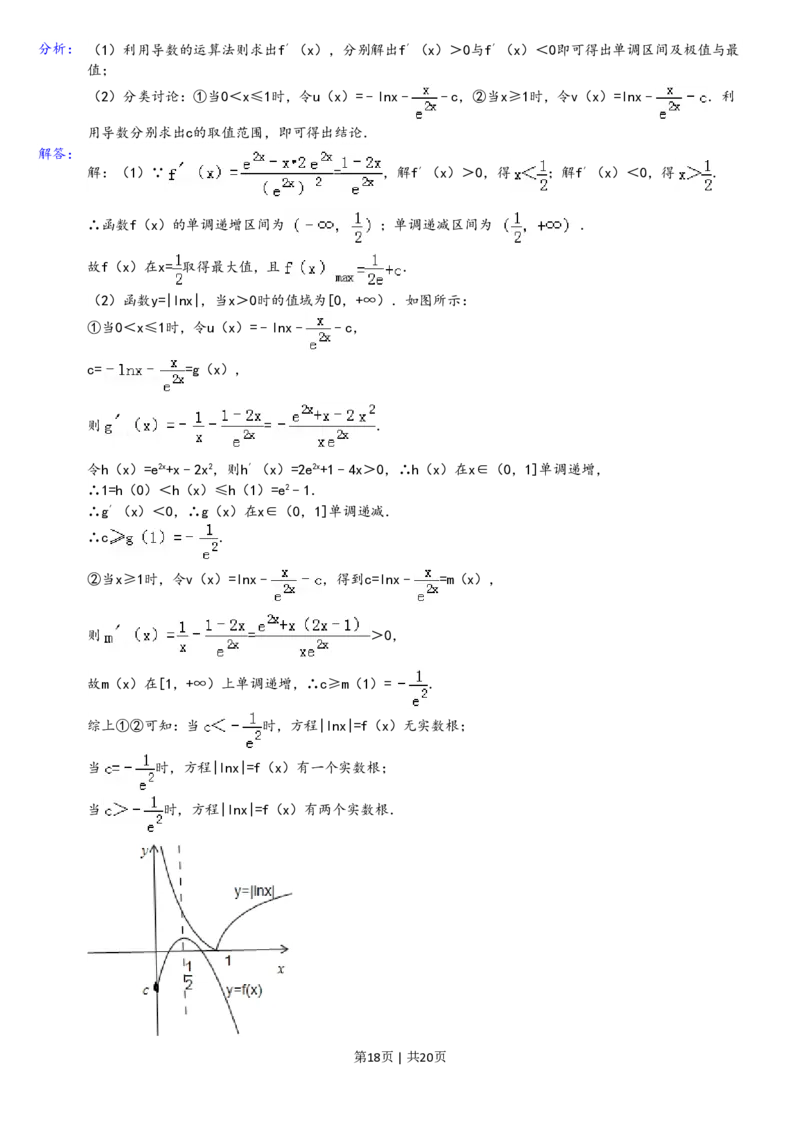
(2)函数y=|lnx|,当x>0时的值域为[0,+∞).如图所示:
①当0<x≤1时,令u(x)=﹣lnx﹣ ﹣c,
c= =g(x),
则 = .
令h(x)=e2x+x﹣2x2,则h′(x)=2e2x+1﹣4x>0,∴h(x)在x∈(0,1]单调递增,
∴1=h(0)<h(x)≤h(1)=e2﹣1.
∴g′(x)<0,∴g(x)在x∈(0,1]单调递减.
∴c .
②当x≥1时,令v(x)=lnx﹣ ,得到c=lnx﹣ =m(x),
则 = >0,
故m(x)在[1,+∞)上单调递增,∴c≥m(1)= .
综上①②可知:当 时,方程|lnx|=f(x)无实数根;
当 时,方程|lnx|=f(x)有一个实数根;
当 时,方程|lnx|=f(x)有两个实数根.
第18页 | 共20页点评: 本题综合考查了利用导数研究函数的单调性、极值最值、数形结合的思想方法、分类讨论的思想方法等基
础知识与基本技能,考查了推理能力和计算能力及其化归思想方法.
22.(13分)(2013•山东)椭圆C: 的左右焦点分别是F,F,离心率为 ,过F且垂直
1 2 1
于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接PF,PF,设∠FPF的角平分线PM交C的长轴于点M(m,0),求m的
1 2 1 2
取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF,PF的斜率分别为
1 2
k,k,若k≠0,试证明 为定值,并求出这个定值.
1 2
考点: 直线与圆锥曲线的关系;直线的斜率;椭圆的标准方程;椭圆的简单性质.
3253948
专题: 压轴题;圆锥曲线的定义、性质与方程.
分析:
(1)把﹣c代入椭圆方程得 ,解得 ,由已知过F且垂直于x轴的直线被椭圆C截得的线段
1
长为1,可得 .再利用 ,及a2=b2+c2即可得出;
(2)设|PF|=t,|PF|=n,由角平分线的性质可得 ,利用椭圆的定义可得t+n=2a=4,
1 2
消去t得到 ,化为 ,再根据a﹣c<n<a+c,即可得到m的取值范围;
(3)设P(x,y),不妨设y>0,由椭圆方程 ,取 ,利用导数即可得到切线的斜
0 0 0
率,再利用斜率计算公式即可得到k,k,代入即可证明结论.
1 2
解答:
解:(1)把﹣c代入椭圆方程得 ,解得 ,
∵过F且垂直于x轴的直线被椭圆C截得的线段长为1,∴ .
1
又 ,联立得 解得 ,
∴椭圆C的方程为 .
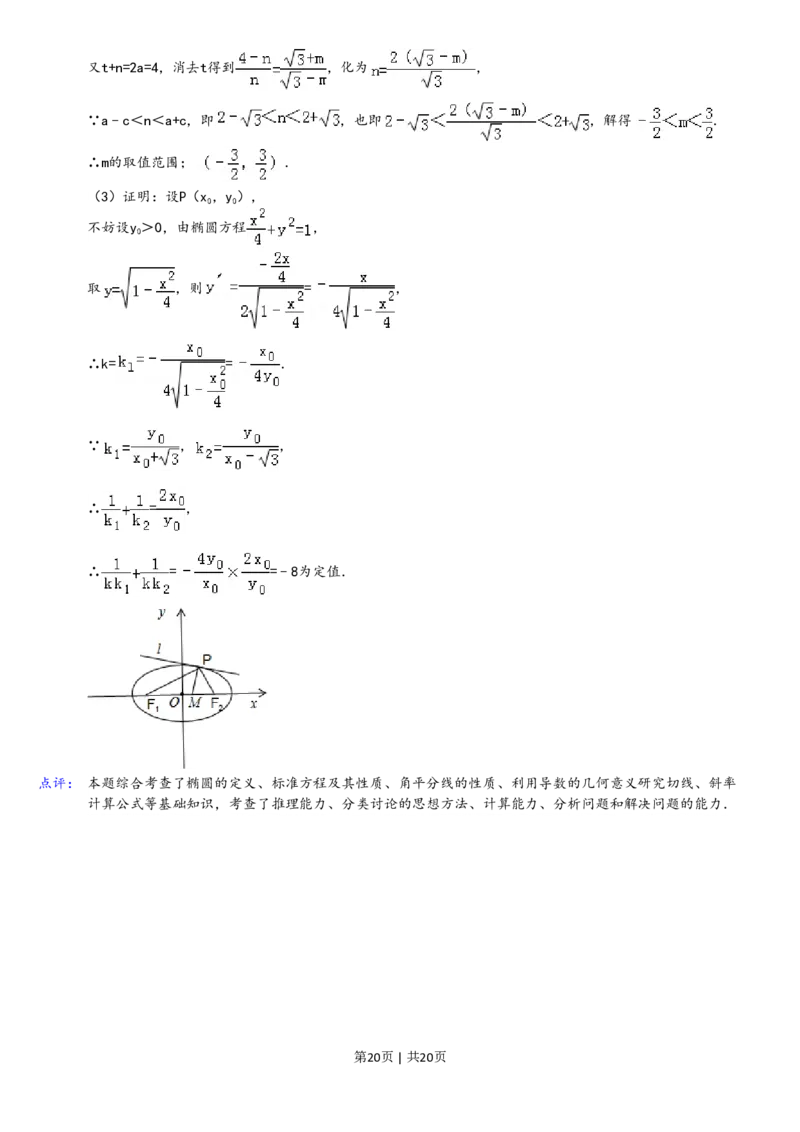
(2)如图所示,设|PF|=t,|PF|=n,
1 2
由角平分线的性质可得 ,
第19页 | 共20页又t+n=2a=4,消去t得到 ,化为 ,
∵a﹣c<n<a+c,即 ,也即 ,解得 .
∴m的取值范围; .
(3)证明:设P(x,y),
0 0
不妨设y>0,由椭圆方程 ,
0
取 ,则 = ,
∴k= = .
∵ , ,
∴ = ,
∴ = =﹣8为定值.
点评: 本题综合考查了椭圆的定义、标准方程及其性质、角平分线的性质、利用导数的几何意义研究切线、斜率
计算公式等基础知识,考查了推理能力、分类讨论的思想方法、计算能力、分析问题和解决问题的能力.
第20页 | 共20页