文档内容
2013年全国统一高考数学试卷(理科)(新课标Ⅰ)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只
有一个是符合题目要求的.
1.(5分)已知集合A={x|x2﹣2x>0},B={x|﹣ <x< },则( )
A.A∩B=∅ B.A∪B=R C.B⊆A D.A⊆B
2.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为( )
A.﹣4 B. C.4 D.
3.(5分)为了解某地区中小学生的视力情况,拟从该地区的中小学生中抽取
部分学生进行调查,事先已经了解到该地区小学、初中、高中三个学段学生
的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中
,最合理的抽样方法是( )
A.简单的随机抽样 B.按性别分层抽样
C.按学段分层抽样 D.系统抽样
4.(5分)已知双曲线C: (a>0,b>0)的离心率为 ,则C的渐
近线方程为( )
A.y= B.y= C.y=±x D.y=
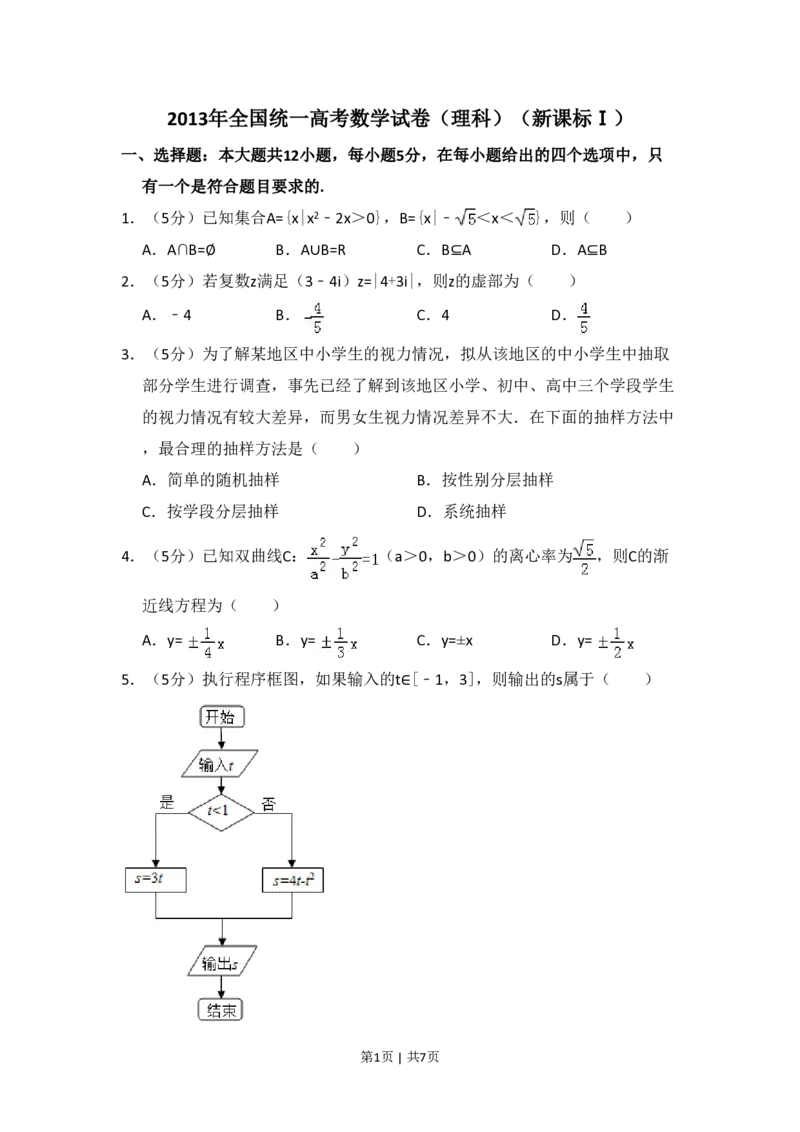
5.(5分)执行程序框图,如果输入的t∈[﹣1,3],则输出的s属于( )
第1页 | 共7页A.[﹣3,4] B.[﹣5,2] C.[﹣4,3] D.[﹣2,5]
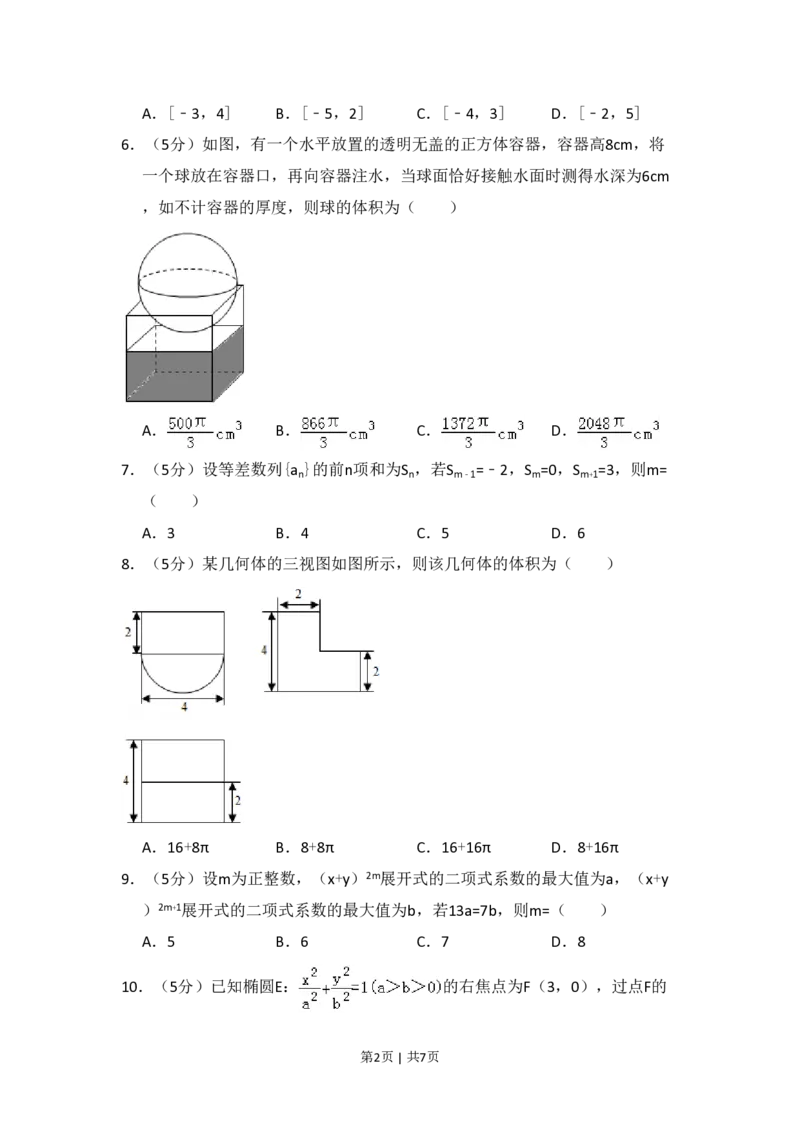
6.(5分)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将
一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm
,如不计容器的厚度,则球的体积为( )
A. B. C. D.
7.(5分)设等差数列{a }的前n项和为S ,若S =﹣2,S =0,S =3,则m=
n n m﹣1 m m+1
( )
A.3 B.4 C.5 D.6
8.(5分)某几何体的三视图如图所示,则该几何体的体积为( )
A.16+8π B.8+8π C.16+16π D.8+16π
9.(5分)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y
)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=( )
A.5 B.6 C.7 D.8
10.(5分)已知椭圆E: 的右焦点为F(3,0),过点F的
第2页 | 共7页直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为(
)
A. B.
C. D.
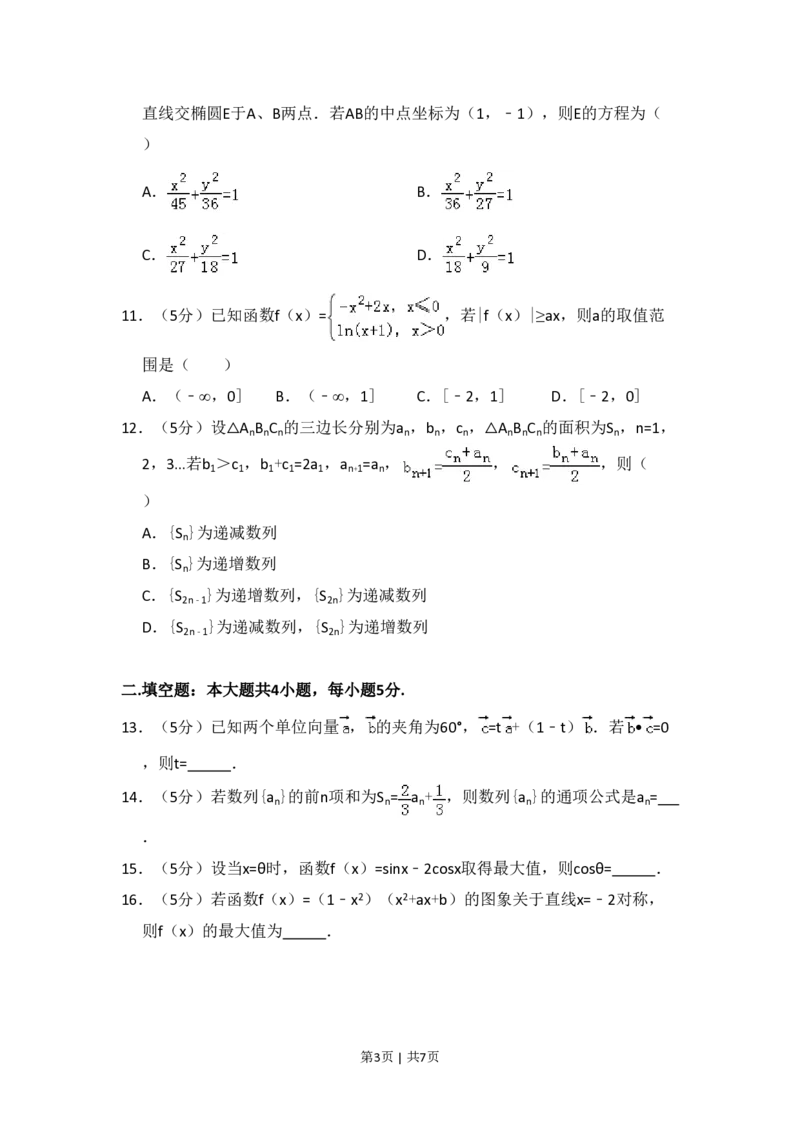
11.(5分)已知函数f(x)= ,若|f(x)|≥ax,则a的取值范
围是( )
A.(﹣∞,0] B.(﹣∞,1] C.[﹣2,1] D.[﹣2,0]
12.(5分)设△A B C 的三边长分别为a ,b ,c ,△A B C 的面积为S ,n=1,
n n n n n n n n n n
2,3…若b >c ,b +c =2a ,a =a , , ,则(
1 1 1 1 1 n+1 n
)
A.{S }为递减数列
n
B.{S }为递增数列
n
C.{S }为递增数列,{S }为递减数列
2n﹣1 2n
D.{S }为递减数列,{S }为递增数列
2n﹣1 2n
二.填空题:本大题共4小题,每小题5分.
13.(5分)已知两个单位向量 , 的夹角为60°, =t +(1﹣t) .若 • =0
,则t= .
14.(5分)若数列{a }的前n项和为S = a + ,则数列{a }的通项公式是a =
n n n n n
.
15.(5分)设当x=θ时,函数f(x)=sinx﹣2cosx取得最大值,则cosθ= .
16.(5分)若函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,
则f(x)的最大值为 .
第3页 | 共7页三、解答题:解答应写出文字说明,证明过程或演算步骤.
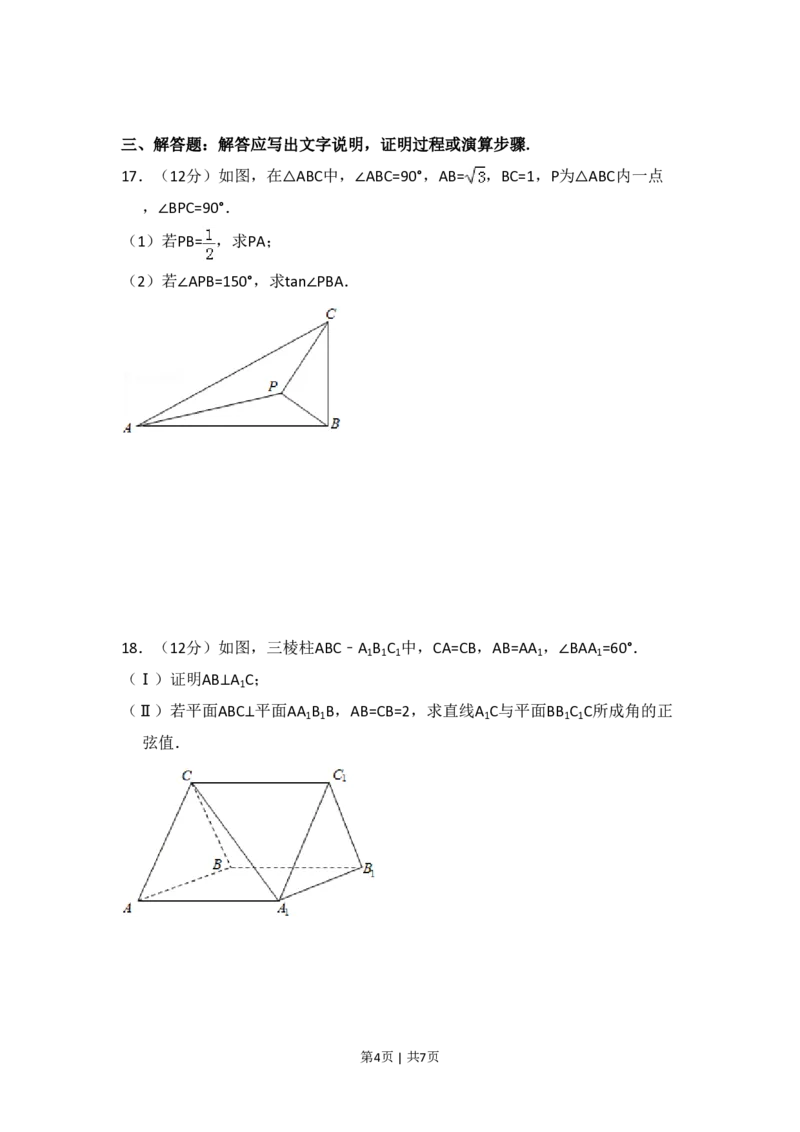
17.(12分)如图,在△ABC中,∠ABC=90°,AB= ,BC=1,P为△ABC内一点
,∠BPC=90°.
(1)若PB= ,求PA;
(2)若∠APB=150°,求tan∠PBA.
18.(12分)如图,三棱柱ABC﹣A B C 中,CA=CB,AB=AA ,∠BAA =60°.
1 1 1 1 1
(Ⅰ)证明AB⊥A C;
1
(Ⅱ)若平面ABC⊥平面AA B B,AB=CB=2,求直线A C与平面BB C C所成角的正
1 1 1 1 1
弦值.
第4页 | 共7页19.(12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4
件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任
取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产
品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这
批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的产品是
优质品的概率都为 ,且各件产品是否为优质品相互独立.
(Ⅰ)求这批产品通过检验的概率;
(Ⅱ)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批
产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
20.(12分)已知圆M:(x+1)2+y2=1,圆N:(x﹣1)2+y2=9,动圆P与圆M外
切并与圆N内切,圆心P的轨迹为曲线C.
(Ⅰ)求C的方程;
(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半
径最长时,求|AB|.
第5页 | 共7页21.(12分)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和
曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若x≥﹣2时,f(x)≤kg(x),求k的取值范围.
四、请考生在第22、23、24题中任选一道作答,并用2B铅笔将答题卡上所选的
题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂
的首题进行评分,不涂,按本选考题的首题进行评分.
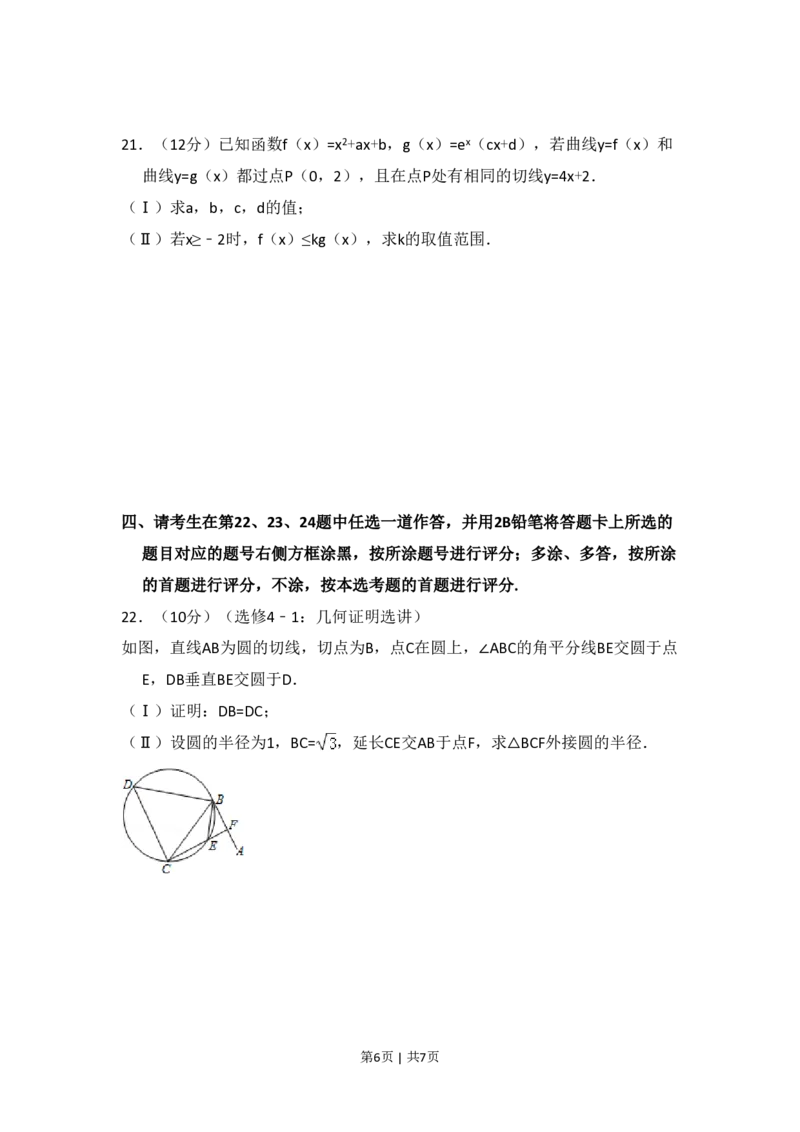
22.(10分)(选修4﹣1:几何证明选讲)
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点
E,DB垂直BE交圆于D.
(Ⅰ)证明:DB=DC;
(Ⅱ)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
第6页 | 共7页23.已知曲线C 的参数方程为 (t为参数),以坐标原点为极点,x
1
轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=2sinθ.
2
(1)把C 的参数方程化为极坐标方程;
1
(2)求C 与C 交点的极坐标(ρ≥0,0≤θ<2π).
1 2
24.已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>﹣1,且当x∈[﹣ , ]时,f(x)≤g(x),求a的取值范围.
第7页 | 共7页