文档内容
2024 年上海市高考数学试卷(网络回忆版)
“试题来自网络,非官方渠道,学科网不对真实性负责,请自行鉴别”
2024.06
一、填空题(本大题共有12题,满分54分.其中第1-6题每题4分,第7-12题每题满分5分)
考生应在答题纸相应编号的空格内直接填写结果.
1. 设全集 ,集合 ,则 ______.
2. 已知 则 ______.
3. 已知 则不等式 的解集为______.
4. 已知 , ,且 是奇函数,则 ______.
5. 已知 ,且 ,则 的值为______.
6. 在 的二项展开式中,若各项系数和为32,则 项的系数为______.
7. 已知抛物线 上有一点 到准线的距离为9,那么点 到 轴的距离为______.
8. 某校举办科学竞技比赛,有 3种题库, 题库有5000道题, 题库有4000道题, 题库有
3000道题.小申已完成所有题,已知小申完成 题库的正确率是0.92, 题库的正确率是0.86, 题库的
正确率是0.72.现他从所有的题中随机选一题,正确率是______.
9. 已知虚数 ,其实部为1,且 ,则实数 为______.
10. 设集合 中的元素皆为无重复数字的三位正整数,且元素中任意两个不同元素之积皆为偶数,求集合
中元素个数的最大值______.
11. 已 知 点 B 在 点 C 正 北 方 向 , 点 D 在 点 C 的 正 东 方 向 , , 存 在 点 A 满 足
,则 ______(精确到0.1度)12. 无穷等比数列 满足首项 ,记 ,若对任意正整数
集合 是闭区间,则 的取值范围是______.
二、选择题(本大题共有 4题,满分18分,其中第13-14题每题满分4分,第15-16题每题
满分5分)每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格
涂黑,选对得满分,否则一律得零分.
13. 已知气候温度和海水表层温度相关,且相关系数为正数,对此描述正确的是( )
A. 气候温度高,海水表层温度就高
B. 气候温度高,海水表层温度就低
C. 随着气候温度由低到高,海水表层温度呈上升趋势
D. 随着气候温度由低到高,海水表层温度呈下降趋势
14. 下列函数的最小正周期是 的是( )
A. B.
.
C D.
15. 定义一个集合 ,集合中的元素是空间内的点集,任取 ,存在不全为0的实数 ,
使得 .已知 ,则 的充分条件是( )
A. B.
C. D.
16. 已知函数 的定义域为R,定义集合 ,在使得的所有 中,下列成立的是( )
A. 存在 是偶函数 B. 存在 在 处取最大值
C. 存在 是严格增函数 D. 存在 在 处取到极小值
三、解答题(本大题共有 5题,满分78分)解下列各题必须在答题纸相应编号的规定区域内
写出必要的步骤
的
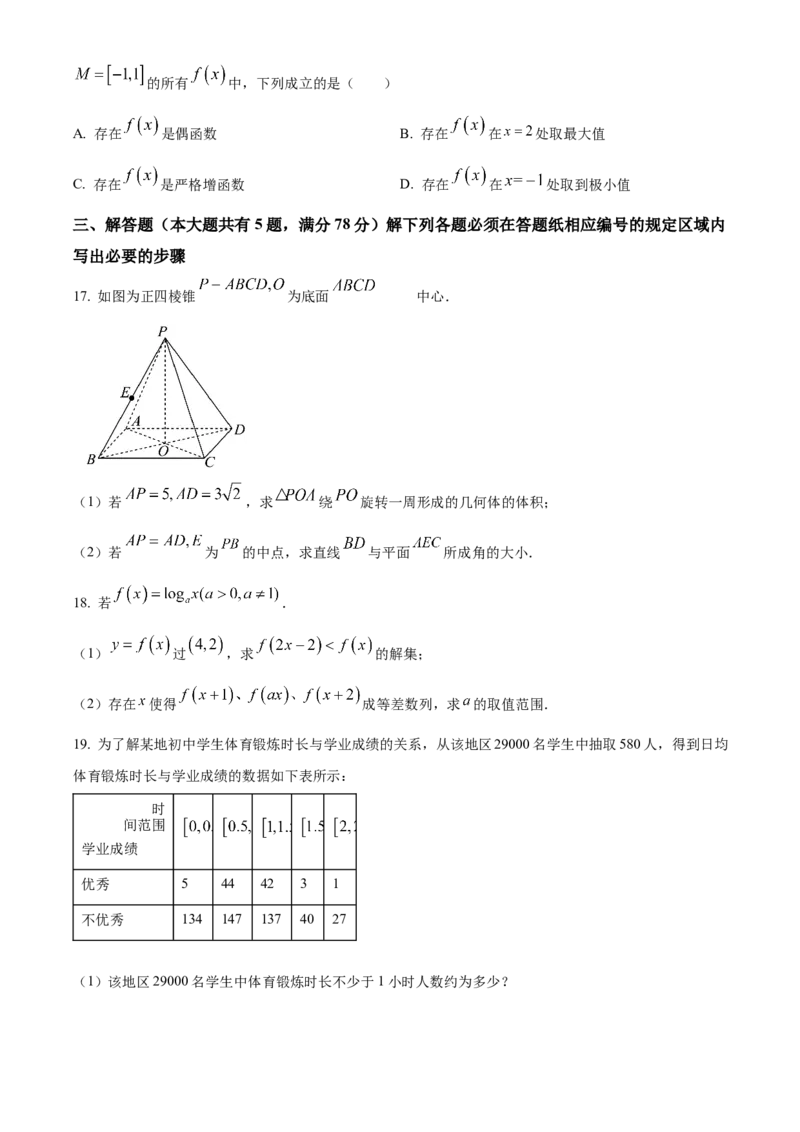
17. 如图为正四棱锥 为底面 中心.
(1)若 ,求 绕 旋转一周形成的几何体的体积;
(2)若 为 的中点,求直线 与平面 所成角的大小.
18. 若 .
(1) 过 ,求 的解集;
(2)存在 使得 成等差数列,求 的取值范围.
19. 为了解某地初中学生体育锻炼时长与学业成绩的关系,从该地区29000名学生中抽取580人,得到日均
体育锻炼时长与学业成绩的数据如下表所示:
时
间范围
学业成绩
优秀 5 44 42 3 1
不优秀 134 147 137 40 27
(1)该地区29000名学生中体育锻炼时长不少于1小时人数约为多少?的
(2)估计该地区初中学生日均体育锻炼 时长(精确到0.1)
(3)是否有 的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
(附: 其中 , .)
20. 已知双曲线 左右顶点分别为 ,过点 的直线 交双曲线 于
两点.
(1)若离心率 时,求 的值.
(2)若 为等腰三角形时,且点 在第一象限,求点 的坐标.
(3)连接 并延长,交双曲线 于点 ,若 ,求 的取值范围.
21. 对于一个函数 和一个点 ,令 ,若 是
取到最小值的点,则称 是 在 的“最近点”.
(1)对于 ,求证:对于点 ,存在点 ,使得点 是 在 的“最近点”;
(2)对于 ,请判断是否存在一个点 ,它是 在 的“最近点”,且直线 与
在点 处的切线垂直;
(3)已知 在定义域R上存在导函数 ,且函数 在定义域R上恒正,设点
, .若对任意 的,存在点 同时是 在
的“最近点”,试判断 的单调性.