2013年高考数学试卷（理）（湖北）（解析卷）_数学历年高考真题_新·PDF版2008-2025·高考数学真题_数学（按省份分类）2008-2025_2012-2025·（湖北）数学高考真题

本解析为学科网名师解析团队原创，授权学科网独家使用，如有盗用，依法追责！ 一、选择题：本大题共 10小题，每小题 5分，共 50分. 在每小题给出的四个选项中， 只有一项是符合题目要求的. 2i 1. 在复平面内，复数z  (i为虚数单位)的共轭复数对应的点位于 1i A.第一象限 B. 第二象限 C. 第三象限 D.第四象限 第1页 | 共17页 1    2．已知集合为R，集合A x|( )x 1，B  x| x2 6x80 ，则AC B   2  R A.  x| x 0  B.  x|2 x  4  C.  x|0 x  2或x  4  D.  x|0 x  2或x  4  3．在一次跳伞训练中，甲、乙两位学员各跳一次．设命题p是“甲降落在指定范围”，q是“乙降 落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为 A．(Øp)∨(Øq) B． p∨(Øq) C．(Øp)∧(Øq) D． p∨q 4．将函数y  3cosx+sinx(xÎR)的图像向左平移m(m0)个单位长度后，所得到的图像关于 y轴对称，则m的最小值是 p p p 5p A． B． C． D． 12 6 3 6 [答案] B p p [解析] 易知y 2sin(x+ )，向左平移m个单位后得y2sin(x+ +m)，图像关于y轴对称， 3 3 p p p p 则令 +m +kp,kÎZ ,得x +kp，又m0，故m的最小值为 .选B. 3 2 6 6 [学科网考点定位]本题考查三角函数的图像及平移变换，考查分析问题能力及转化思想. p x2 y2 y2 x2 5．已知0q ，则双曲线C :  1与C :  1的 4 1 cos2q sin2q 2 sin2q sin2qtan2q A．实轴长相等 B．虚轴长相等 C．焦距相等 D．离心率相等 第2页 | 共17页uuur uuur 6．已知点A（-1,1）、B（1,2）、C（-2,1）、D（3,4），则向量AB和CD 方向上的投影为 3 2 3 15 3 2 3 15 A． B． C． D． 2 2 2 2 7.一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度 25 v(t)73t+ (t的单位：s,v的单位：m/s)行驶至停止，在此期间汽车继续行驶的距离（单 1+t 位：m）是 11 A．1+25ln5 B．8+25ln C．4+25ln5 D．4+50ln2 3 [学科网考点定位]本题考查导数及定积分的意义，考查分析问题和计算问题的能力. 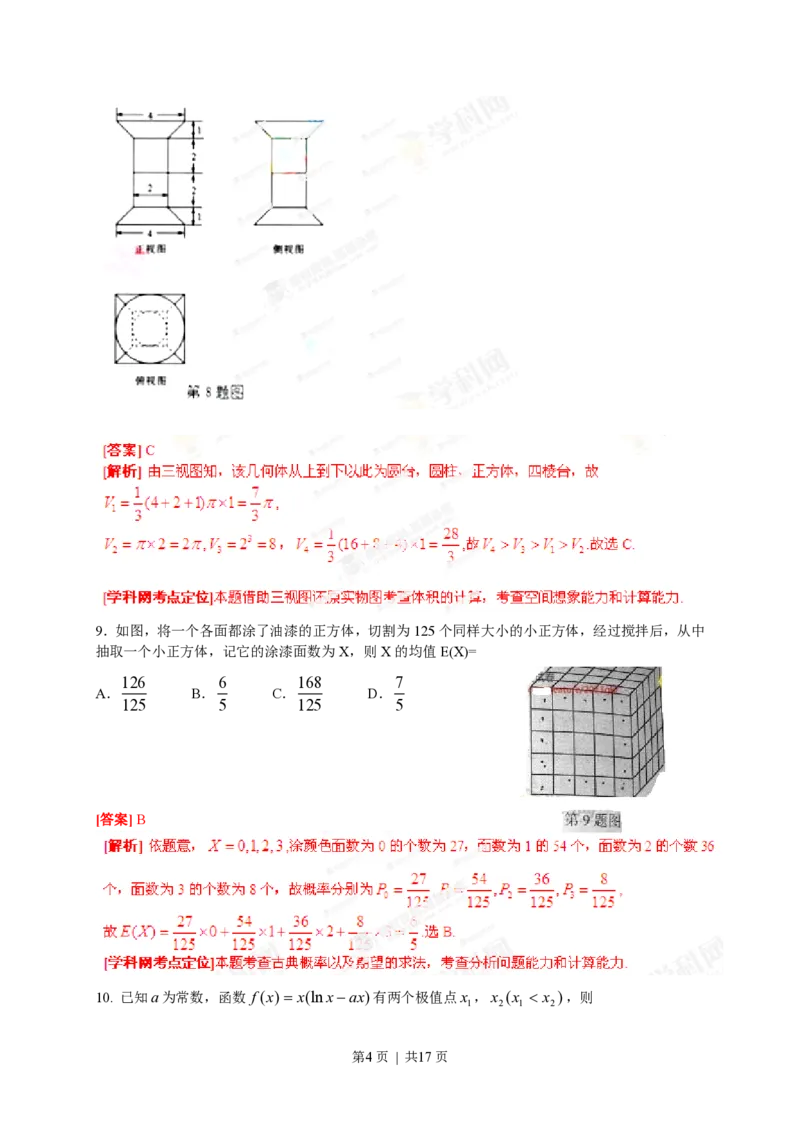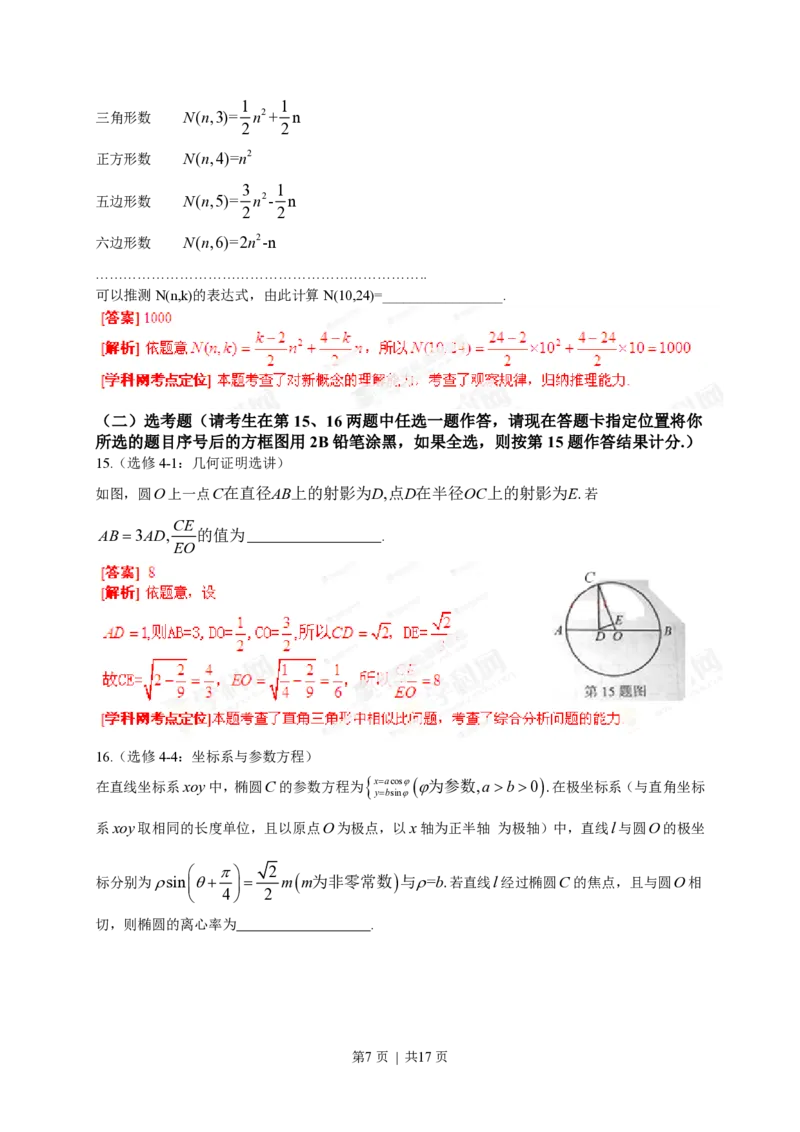8．一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别为 V，V，V，V，这四个几何体为旋转体，下面两个简单几何体均为多面体，则有 1 2 3 4 A.V V V V B.V V V V C.V V V V D.V V V V 1 2 4 3 1 3 2 4 2 1 3 4 2 3 1 4 第3页 | 共17页9．如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中 抽取一个小正方体，记它的涂漆面数为X，则X的均值E(X)= 126 6 168 7 A． B． C． D． 125 5 125 5 [答案] B 10. 已知a为常数，函数 f(x)  x(lnxax)有两个极值点x ，x (x  x )，则 1 2 1 2 第4页 | 共17页1 1 A． f(x ) 0 ， f(x )   B. f(x )0 ， f(x )  1 2 2 1 2 2 1 1 C． f(x ) 0 ， f(x )  D. f(x )0 ， f(x )   1 2 2 1 2 2 二.填空题：本大题共 6 小题，考生共需作答 5 小题，每小题 5 分，共 25 分，请将答案 填在答题卡的对应题号的位置上，答错位置，书写不清，模棱两可均不得分. 11．从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直 方图如图所示。 （1）直方图中x的值为___________； （2）在这些用户中，用电量落在区间[100,250)内的户数为___________. 力. 12.阅读如图所示的程序框图，运行相应的程序，输出的结果i=___________。 第5页 | 共17页14．古希腊毕达哥拉斯的数学家研究过各种多边形数，如三角形数1,3,6,10,…,第n个三角形数为 n(n+1) 1 1 = n2+ n，记第n个k边形数为N(n,k)(k 3)，以下列出了部分k边形数中第n个数的 2 2 2 表达式： 第6页 | 共17页1 1 三角形数 N(n,3)= n2+ n 2 2 正方形数 N(n,4)=n2 3 1 五边形数 N(n,5)= n2- n 2 2 六边形数 N(n,6)=2n2-n …………………………………………………………….. 可以推测N(n,k)的表达式，由此计算N(10,24)=_________________. （二）选考题（请考生在第 15、16两题中任选一题作答，请现在答题卡指定位置将你 所选的题目序号后的方框图用 2B铅笔涂黑，如果全选，则按第 15题作答结果计分.） 15.（选修4-1：几何证明选讲） 如图，圆O上一点C在直径AB上的射影为D,点D在半径OC上的射影为E.若 CE AB3AD, 的值为 . EO 16.（选修4-4：坐标系与参数方程） 在直线坐标系xoy中，椭圆C的参数方程为 xacosjj为参数,ab0.在极坐标系（与直角坐标 ybsinj 系xoy取相同的长度单位，且以原点O为极点，以x轴为正半轴 为极轴）中，直线l与圆O的极坐 æ pö 2 标分别为rsin ç q+ ÷  mm为非零常数与r=b.若直线l经过椭圆C的焦点，且与圆O相 è 4ø 2 切，则椭圆的离心率为 . 第7页 | 共17页三、解答题:本大题共 6 小题，共 75 分.解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分12分） 在DABC中，角A、B、C对应的边分别为a,b,c.已知cos2A3cos(B+C)1. （I）求角A的大小； （II）若DABC的面积S 5 3,b5,求sinBsinC的值. π 因为0 Aπ，所以A . 3 第8页 | 共17页18.（本小题满分12分） 已知等比数列a 满足： a a 10,aa a 125. n 2 3 1 2 3 （I）求数列a 的通项公式； n 1 1 1 （II）是否存在正整数m,使得 + +××××××+ 1?若存在，求m的最小值；若不存在，说明理 a a a 1 2 n 由. 19.（本小题满分12分） 如图，AB是圆O的直径,点C是圆O上异于A、B的点，直线PC ^平面ABC, E,F分别为PA,PB的中点. （I）记平面BEF与平面ABC的交线为l，是判断l与平面PAC的位置关系，并加以说明； r 1 r （II）设（I）中的直线l与圆O的另一个交点为D,且点Q满足DQ CP.记直线 2 PQ与平面ABC所成的角为O,异面直线所成的锐角为o，二面角 ElC的大小为b，求证：sinqsinasinb. 第9页 | 共17页连接BE ，BF ，因为BF Ì平面PBC ，所以l ^BF . 故ÐCBF 就是二面角ElC 的平面角，即ÐCBF b. 第10页 | 共17页[学科网考点定位] 本题考查线面位置关系判断及线面角的求法，考查空间想象能力. 20.（本小题满分12分） 第11页 | 共17页假设每天从甲地去乙地的旅客人数X是服从正态分布N  800,502的随机变量， 记一天中从甲地去乙地的旅客人数不超过900的概率为P. n 求P 的值； n （I）（参考数据：若X N  m,s2 ,有Pms X m+s0.6826,） : Pm2s X m+2s0.9544,Pm3s X m+3s0.9974. （II）某客运公司用A、B两种型号的车辆承担甲、乙两地间的长途客运业务，每年每天往返一次， A、B两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1600元/辆和2400 元/辆.公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7辆。若每天要以不 小于P 的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最小，那么应配备 0 A型车、B型车各多少辆？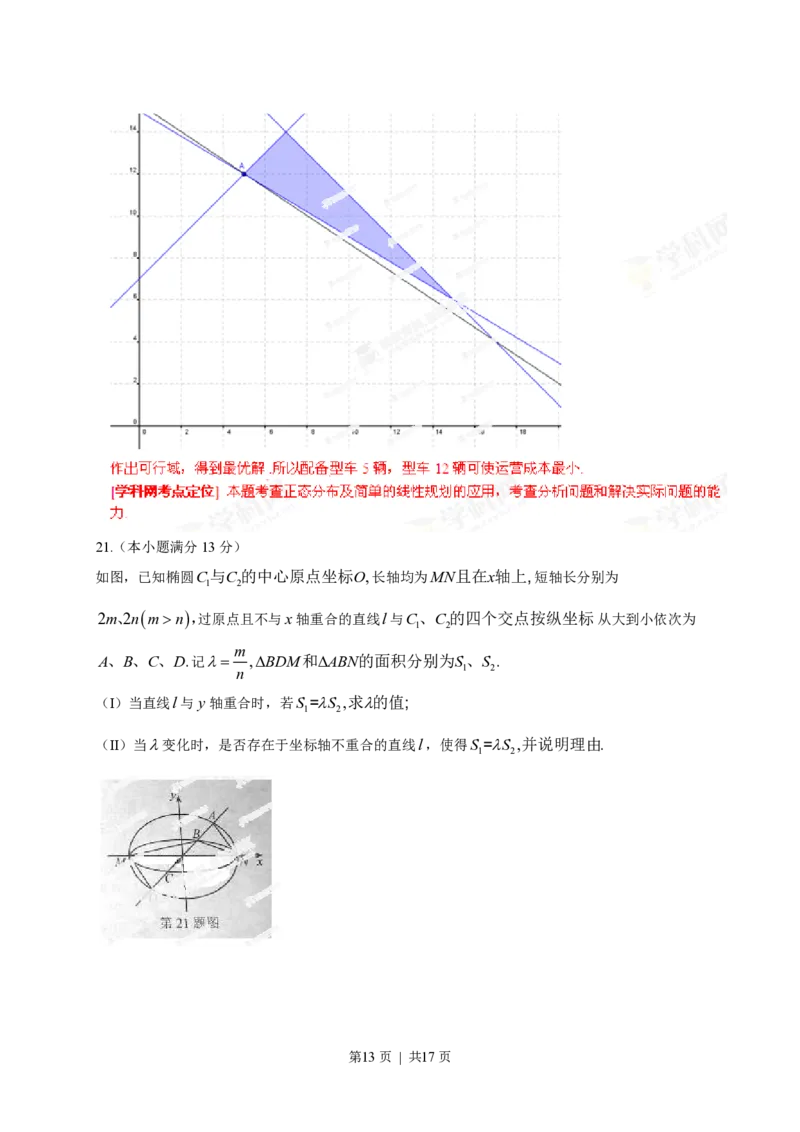 第12页 | 共17页21.（本小题满分13分） 如图，已知椭圆C与C的中心原点坐标O,长轴均为MN且在x轴上,短轴长分别为 1 2 2m、2nmn，过原点且不与x轴重合的直线l与C、C的四个交点按纵坐标从大到小依次为 1 2 m A、B、C、D.记l ,DBDM和DABN的面积分别为S、S . n 1 2 （I）当直线l与y轴重合时，若S =lS ,求l的值; 1 2 （II）当l变化时，是否存在于坐标轴不重合的直线l，使得S =lS ,并说明理由. 1 2 第13页 | 共17页不妨设 直线l：ykx (k 0)， 第14页 | 共17页1 1 S |BD| 又S  |BD|d ，S  |AB|d ，所以 1  l. 1 2 1 2 2 2 S |AB| 2 第15页 | 共17页22.（本小题满分14分） 设n为正整数，r为正有理数. （I）求函数 f x1+xr+1 r+1x1x1的最小值； nr+1n1r+2 n+1r+1 nr+1 （II）证明： nr  ; r+1 r+1 é 3ù （III）设xÎR，记x为不小于x的最小整数，例如2=2,p=4,  =-1. ê ú ë 2û 令S  3 81+ 3 82+ 3 83+××××××+3125,求S的值. 4 4 4 4 （参考数据：803 344.7,813 350.5,1243 618.3,1263 631.7.） （III）先放缩，再累加整理即可证明. 第16页 | 共17页第17页 | 共17页