文档内容
2013年普通高等学校招生全国统一考试(天津卷)
文 科 数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分, 共150分. 考试用时120分钟.
第Ⅰ卷1至2页, 第Ⅱ卷3至5页.
第Ⅰ卷
参考公式:
如果事件A, B互斥, 那么
P(AÈB)=P(A)+P(B)
·棱柱的体积公式V = Sh,
其中S表示棱柱的底面面积, h表示棱柱的高.
·如果事件A, B相互独立, 那么
P(AB)=P(A)P(B)
4
·球的体积公式 V = pR3.
3
其中R表示球的半径.
一.选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 已知集合A = {x∈R| |x|≤2}, B = {x∈R| x≤1}, 则 AÇB=
(A) (-¥,2] (B) [1,2] (C) [-2,2] (D) [-2,1]
ì3x+ y-6³0,
(2) 设变量x, y满足约束条件ï íx- y-2£0, 则目标函数z = y-2x的最小值为
ï
îy-3£0,
(A) -7 (B) -4
(C) 1 (D) 2
(3) 阅读右边的程序框图, 运行相应的程序, 则输出n的值为
第1页 | 共5页(A) 7 (B) 6
(C) 5 (D) 4
(4) 设 a,bÎR, 则 “(a-b)a2 <0”是“a0,b>0) 的一个焦点,
a2 b2
且双曲线的离心率为2, 则该双曲线的方程为 .
(12) 在平行四边形ABCD中, AD = 1, ÐBAD=60°, E为CD的中点. 若u A u C ur · u B u E ur =1, 则AB的长为 .
(13) 如图, 在圆内接梯形ABCD中, AB//DC,
过点A作圆的切线与CB的延长线交于点E. 若AB = AD = 5, BE = 4,
则弦BD的长为 .
(14) 设a + b = 2, b>0, 则 1 + |a|的最小值为 .
2|a| b
三.解答题: 本大题共6小题, 共70分. 解答应写出文字说明, 证明过程或演算步骤.
(15) (本小题满分13分)
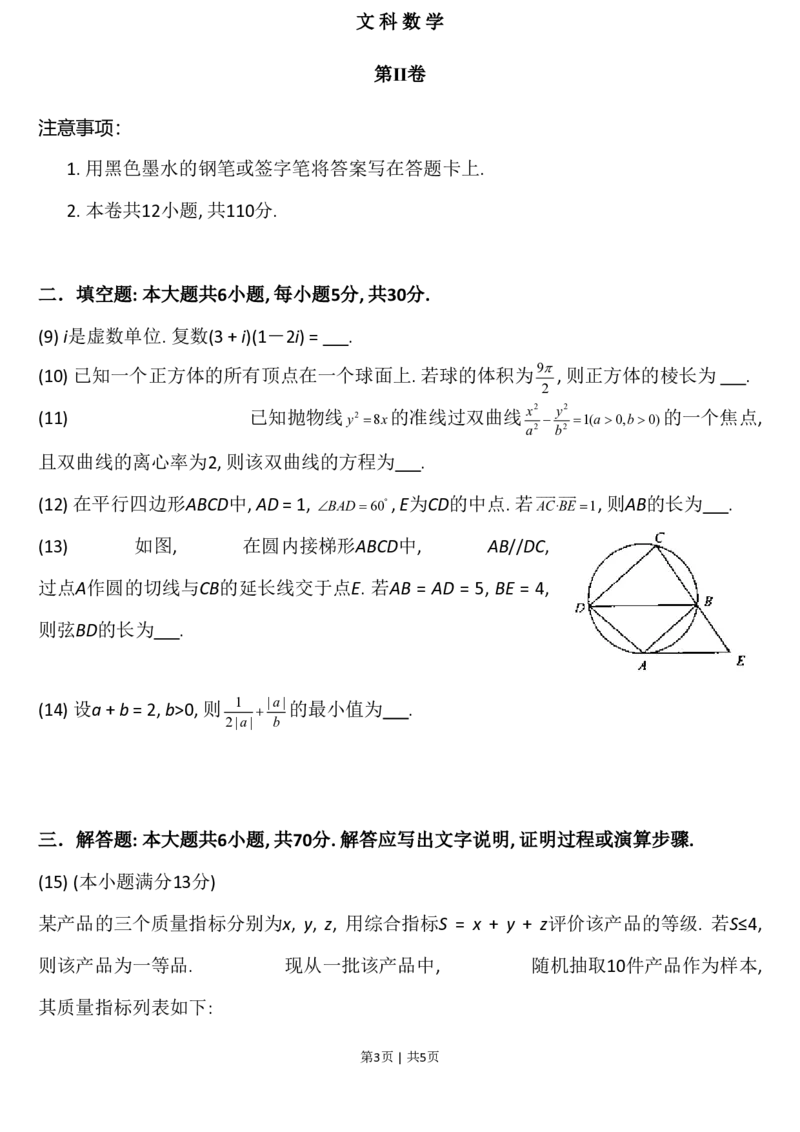
某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z评价该产品的等级. 若S≤4,
则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本,
其质量指标列表如下:
第3页 | 共5页产品编号 A A A A A
1 2 3 4 5
质量指标(x, y, z) (1,1,2) (2,1,1) (2,2,2) (1,1,1) (1,2,1)
产品编号 A A A A A
6 7 8 9 10
质量指标(x, y, z) (1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2)
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取2件产品,
(⒈) 用产品编号列出所有可能的结果;
(⒉) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”,
求事件B发生的概率.
(16) (本小题满分13分)
在△ABC中, 内角A, B, C所对的边分别是a, b, c. 已知 bsinA=3csinB, a = 3, cosB= 2 .
3
(Ⅰ) 求b的值;
(Ⅱ) 求 sin æ ç2B- pö ÷ 的值.
è 3ø
(17) (本小题满分13分)
如图, 三棱柱ABC-A B C 中,
1 1 1
侧棱A A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC,
1
A C 的中点.
1 1
(Ⅰ) 证明EF//平面A CD;
1
(Ⅱ) 证明平面A CD⊥平面A ABB ;
1 1 1
(Ⅲ) 求直线BC与平面A CD所成角的正弦值.
1
(18) (本小题满分13分)
设椭圆 x2 + y2 =1(a>b>0) 的左焦点为F, 离心率为 3 ,
a2 b2 3
第4页 | 共5页过点F且与x轴垂直的直线被椭圆截得的线段长为4 3
.
3
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设A, B分别为椭圆的左,右顶点, 过点F且斜率为k的直线与椭圆交于C, D两点. 若
u A u C ur · u D uu B r + u A u D ur ·C uu B ur =8, 求k的值.
(19) (本小题满分14分)
已知首项为3 的等比数列 {a } 的前n项和为 S (nÎN*), 且 -2S ,S ,4S 成等差数列.
2 n n 2 3 4
(Ⅰ) 求数列
{a }
的通项公式;
n
(Ⅱ) 证明 S + 1 £ 13 (nÎN*).
n S 6
n
(20) (本小题满分14分)
ì x3 -(a+5)x, x£0,
设 aÎ[-2,0], 已知函数 f(x)= ï í a+3
ïx3 - x2 +ax, x>0.
î 2
(Ⅰ) 证明 f(x) 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
(Ⅱ) 设曲线 y= f(x) 在点 P(x, f(x))(i=1,2,3) 处的切线相互平行, 且 xx x ¹0, 证明 x +x +x > 1 .
i i i 1 2 3 1 2 3 3
第5页 | 共5页