文档内容
2013年普通高等学校招生全国统一考试(天津卷)
文 科 数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分, 共150分. 考试用时120分钟.
第Ⅰ卷1至2页, 第Ⅱ卷3至5页.
第Ⅰ卷
参考公式:
如果事件A, B互斥, 那么
P(AÈB)=P(A)+P(B)
·棱柱的体积公式V = Sh,
其中S表示棱柱的底面面积, h表示棱柱的高.
·如果事件A, B相互独立, 那么
P(AB)=P(A)P(B)
4
·球的体积公式 V = pR3.
3
其中R表示球的半径.
一.选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 已知集合A = {x∈R| |x|≤2}, B = {x∈R| x≤1}, 则 AÇB=
(A) (-¥,2] (B) [1,2] (C) [-2,2] (D) [-2,1]
ì3x+ y-6³0,
(2) 设变量x, y满足约束条件ï íx- y-2£0, 则目标函数z = y-2x的最小值为
ï
îy-3£0,
(A) -7 (B) -4
(C) 1 (D) 2
(3) 阅读右边的程序框图, 运行相应的程序, 则输出n的值为
第1页 | 共10页(A) 7 (B) 6
(C) 5 (D) 4
(4) 设 a,bÎR, 则 “(a-b)a2 <0”是“a0,b>0) 的一个焦点,
a2 b2
且双曲线的离心率为2, 则该双曲线的方程为 .
(12) 在平行四边形ABCD中, AD = 1, ÐBAD=60°, E为CD的中点. 若u A u C ur · u B u E ur =1, 则AB的长为 .
(13) 如图, 在圆内接梯形ABCD中, AB//DC,
过点A作圆的切线与CB的延长线交于点E. 若AB = AD = 5, BE = 4,
则弦BD的长为 .
(14) 设a + b = 2, b>0, 则 1 + |a|的最小值为 .
2|a| b
三.解答题: 本大题共6小题, 共70分. 解答应写出文字说明, 证明过程或演算步骤.
(15) (本小题满分13分)
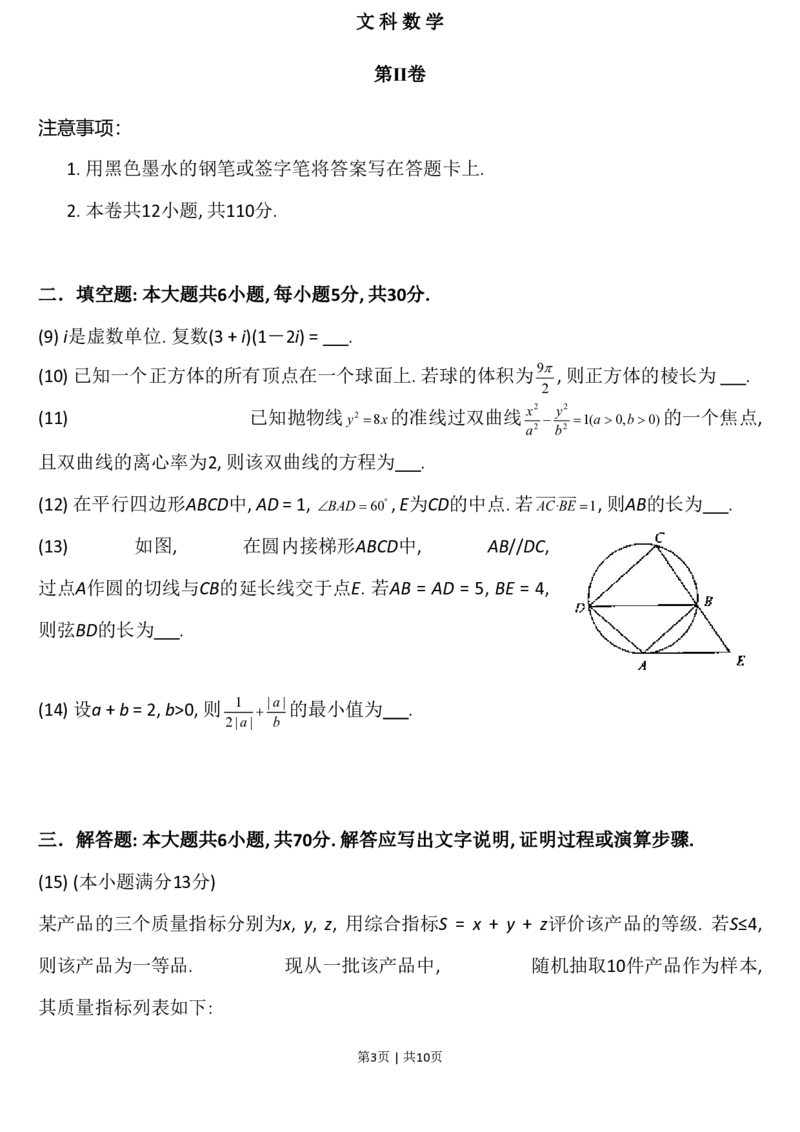
某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z评价该产品的等级. 若S≤4,
则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本,
其质量指标列表如下:
第3页 | 共10页产品编号 A A A A A
1 2 3 4 5
质量指标(x, y, z) (1,1,2) (2,1,1) (2,2,2) (1,1,1) (1,2,1)
产品编号 A A A A A
6 7 8 9 10
质量指标(x, y, z) (1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2)
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取2件产品,
(⒈) 用产品编号列出所有可能的结果;
(⒉) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”,
求事件B发生的概率.
(16) (本小题满分13分)
在△ABC中, 内角A, B, C所对的边分别是a, b, c. 已知 bsinA=3csinB, a = 3, cosB= 2 .
3
(Ⅰ) 求b的值;
(Ⅱ) 求 sin æ ç2B- pö ÷ 的值.
è 3ø
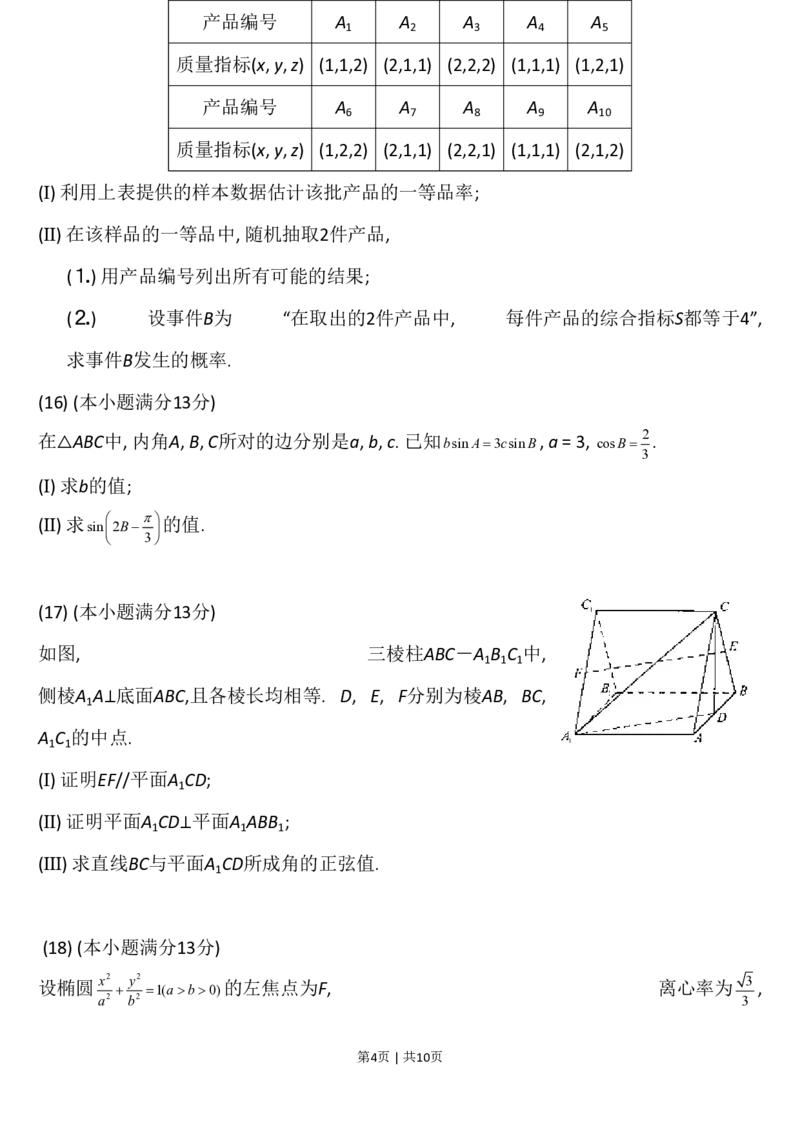
(17) (本小题满分13分)
如图, 三棱柱ABC-A B C 中,
1 1 1
侧棱A A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC,
1
A C 的中点.
1 1
(Ⅰ) 证明EF//平面A CD;
1
(Ⅱ) 证明平面A CD⊥平面A ABB ;
1 1 1
(Ⅲ) 求直线BC与平面A CD所成角的正弦值.
1
(18) (本小题满分13分)
设椭圆 x2 + y2 =1(a>b>0) 的左焦点为F, 离心率为 3 ,
a2 b2 3
第4页 | 共10页过点F且与x轴垂直的直线被椭圆截得的线段长为4 3
.
3
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设A, B分别为椭圆的左,右顶点, 过点F且斜率为k的直线与椭圆交于C, D两点. 若
u A u C ur · u D uu B r + u A u D ur ·C uu B ur =8, 求k的值.
(19) (本小题满分14分)
已知首项为3 的等比数列 {a } 的前n项和为 S (nÎN*), 且 -2S ,S ,4S 成等差数列.
2 n n 2 3 4
(Ⅰ) 求数列
{a }
的通项公式;
n
(Ⅱ) 证明 S + 1 £ 13 (nÎN*).
n S 6
n
(20) (本小题满分14分)
ì x3 -(a+5)x, x£0,
设 aÎ[-2,0], 已知函数 f(x)= ï í a+3
ïx3 - x2 +ax, x>0.
î 2
(Ⅰ) 证明 f(x) 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
(Ⅱ) 设曲线 y= f(x) 在点 P(x, f(x))(i=1,2,3) 处的切线相互平行, 且 xx x ¹0, 证明 x +x +x > 1 .
i i i 1 2 3 1 2 3 3
第5页 | 共10页2013年普通高等学校招生全国统一考试(天津卷)
数学(文史类)参考答案
一、选择题:本题考查基本知识和基础运算。每小题5分。满分40分。
(1)D (2)A (3)D (4)A
(5)C (6)B (7)C (8)A
二、填空题:本题考查基本知识和基本运算。每小题5分,满分30分。
y2
(9)5-5i (10) 3 (11)x2 - =1
3
1 15 3
(12) (13) (14)
2 2 4
三、解答题
(15)本小题主要考查样本估计总体的方法、用列举法计算随机事件所含的基本事件数
、古典概型及其概率计算公式等基础知识。考查数据处理能力和运用概率知识解决简单
问题的能力。满分13分。
(I)解:计算10件产品的综合指标S,如下表:
产品编号 A A A A A A A A A A
1 2 3 4 5 6 7 8 9 10
S 4 4 6 3 4 5 4 5 3 5
6
其中S≤4的有A,A ,A ,A ,A ,A ,共6件,故该样本的一等品率为 =0.6,
1 2 4 5 7 9 10
从而可估计该批产品的一等品率为0.6.
(II)
(i)解:在该样本的一等品中,随机抽取2件产品的所有可能结果为
A A
,
A A
1, 2 1, 4
, A A , A A , A A ,A ,A ,A ,A,A ,A ,A ,A,A ,A,A ,A ,
1, 5 1, 7 1, 9 2 4 2 5 2 7 2 9 4 5 4 7
A ,A,A ,A ,A ,A,A ,A,共15种.
4 9 5 7 5 9 7 9
A A
(ii)解:在该样本的一等品中,综合指标S等于4的产品编号分别为
1
,
2
,
第6页 | 共10页A 5 , A 7 ,则事件B发生的所有可能结果为 A A , A A , A A ,A ,A,A ,A ,
1, 2 1, 5 1, 7 2 5 2 7
A ,A 共6种。
5 7
6 2
所以P(B)= = .
15 5
(16)本小题主要考查同角三角函数的基本关系、二倍角的正弦与余弦公式
、两角差的正弦公式以及正弦定理、余弦定理等基础知识.考查基本运算求解能力.满分1
3分。
a b
(I)解:在DABC中,由 = ,可得bsinA=asinB,又由bsinA=3csinB,可得a=3c,
sinA sinB
又a=3,故c=1.
2
由b2 =a2 +c2 -2accosB,cosB= ,可得b= 6.
3
2 5 1
(II)解:由cosB= ,得sinB= ,进而得cos2B=2cos2 B-1=- ,
3 3 9
4 5
sin2B=2sinBcosB= .
9
æ pö p p 4 5+ 3
所以sin 2B- =sin2Bcos -cos2Bsin = .
ç ÷
è 3ø 3 3 18
(17)本小题主要考查直线与平面平行、平面与平面垂直、直线与平面所成的角等基础
知识。考查空间想象能力、运算求解能力和推理论证能力。满分13分。
(I)证明:如图,在三棱柱ABC -ABC 中,
1 1 1
AC∥AC ,且AC=AC ,连接ED,在DABC中, 因为D,E分别
1 1 1 1
为AB, BC的中点,所
1
以DE= AC且DE∥AC,又因为F为AC 的中点,可得AF = DE,且AF ∥DE,即四边形ADEF
2 1 1 1 1 1
为平行四边形,所以EF ∥DA. 又EF Ë平面ACD,DA Ì平面ACD,所以,EF ∥平面ACD。
1 1 1 1 1
第7页 | 共10页(II)证明:由于底面ABC是正三角形,D为AB的中点,故CD⊥AB,又由于侧棱AA⊥底面
1
ABC,CDÌ平面ABC,所以AA⊥CD,又AA AB= A,因此CD⊥平面AABB ,而CDÌ平面
1 1 I 1 1
ACD,所以平面ACD⊥AABB 。
1 1 1 1
(III)解:在平面AABB 内,过点B作BG⊥AD交直线AD于点G,连接CG.
1 1 1 1
由于平面ACD⊥平面AABB ,而直线AD是平面ACD与平面AABB 的交线,故BG⊥平面
1 1 1 1 1 1 1
ACD。由此得ÐBCG为直线BC与平面ACD所成的角。
1 1
5a 5a
设棱长为a,可得AD = ,由DAAD∽DBGD,易得BG= 。在RtDBGC中,sin
1 2 1 5
BG 5
ÐBCG = = .
BC 5
5
所以直线BC与平面ACD所成角的正弦值为 。
1 5
(18)本小题主要考查椭圆的标准方程和几何性质、直线的方程、向量的运算等基础知
识。考查用代数方法研究圆锥曲线的性质。考查运算求解能力,以及用方程思想解决问
题的能力。满分13分。
c 3
(I)解:设F(-c,0),由 = ,知a= 3c .
a 3
(-c)2 y2 6b
过点F且与x轴垂直的直线为x =-c,代入椭圆方程有 + =1,解得y =± ,于是
a2 b2 3
2 6b 4 3 x2 y2
= ,解得b= 2 ,又a2-c2 =b2,从而a= 3,c=1,所以椭圆的方程为 + =1.
3 3 3 2
(II)解:设点C(x ,y ),D(x ,y ),由F(-1,0)得直线CD的方程为y =k(x+1),由方程组
1 1 2 2
ìy =k(x+1)
ï
íx2 y2 消去y,整理得(2+3k2)x2 +6k2x+3k2 -6=0.
+ =1
ï
î 3 2
6k2 3k2 -6 uuur uuur uuur uuur
求解可得x +x =- ,x x = . 因为A(- 3,0),B( 3,0),所以AC DB+ AD CB=(
1 2 2+3k2 1 2 2+3k2 g g
x + 3,y ) ( 3-x ,-y )+(x + 3,y ) ( 3-x ,-y )
1 1 g 2 2 2 2 g 1 1
=6-2x x -2y y =5-2x x -2k2(x +1)(x +1) -6-
1 2 1 2 1 2 1 2
第8页 | 共10页(2+2k2)x x -2k2(x +x )-2k2
1 2 1 2
2k2 +12
=6+ .
2+3k2
2k2 +12
由已知得6+ =8,解得k =± 2.
2+3k2
(19)本小题主要考查等差数列的概念,等比数列的概念、通项公式、前n项和公式,
数列的基本性质等基础知识.
考查分类讨论的思想,考查运算能力、分析问题和解决问题的能力. 满分14分.
(I)解:设等比数列a 的公比为q,因为-2S ,S ,
n 2 3
a 1
4S 成等差数列,所以S +2S =4S - S ,即S -S =S -S ,可得2a =-a ,于是q= 4 =- .
4 3 2 4 3 4 3 2 4 4 3 a 2
3
3 a 3 æ1ö n-1 3
又a = ,所以等比数列 n 的通项公式为a = ´ =(-1)n-1 .
1 2 n 2 ç è2 ÷ ø g 2n
(II)证明:
ì 1
2+ ,n为奇数,
æ 1ö n 1 æ 1ö n 1 ï ï 2n(2n +1)
S =1- ç - ÷ ,S + =1- ç - ÷ + = í
n è 2ø n S n è 2ø 1- æ - 1ö n ï 2+ 1 ,n为偶数。
ç ÷
è 2ø ï î 2n(2n -1)
1 1 1 13
当n为奇数时,S + 随n的增大而减小,所以S + ≤S + = .
n S n S 1 S 6
n n 1
1 1 1 25
当n为偶数时,S + 随n的增大而减小,所以S + ≤S + = .
n S n S 2 S 12
n n 2
1 13
故对于nÎNn,有 S + ≤ .
n S 6
n
(20)本小题主要考查导数的运算及其几何意义,利用导数研究函数的单调性,考查分
类讨论思想、化归思想、函数思想. 考查综合分析问题和解决问题的能力. 满分14分。
a+3
(I)证明:设函数 f (x)= x3-(a+5)x (x£0), f (x) - x3- x2 +ax (x³0),
1 2 2
① f '(x)=3x2 -(a+5),由aÎ-2,0,从而当-1<x<0时, f '(x)=3x2 -(a+5)
1 1
<3-a-5£0,所以函数 f (x)在区间-1,0内单调递减.
1
②
f '(x)=3x2 -(a+3)x+a=(3x-a)(x-1),由于aÎ-2,0,所以当0<x<1时, f '(x)<0;当
2 2
第9页 | 共10页x>1时, f '(x)>0. 即函数 f (x)在区间0,1内单调递减,在区间(1,+¥)内单调递增.
2 2
综合①,②及 f (0)= f (0),可知函数 f(x)在区间(-
1 2
1,1)内单调递减,在区间(1,+¥)内单调递增.
æ a+3ö
(II)证明:由(I)知 f '(x)在区间(-¥,0)内单调递减,在区间 0, 内单调递减,在
ç ÷
è 6 ø
æa+3 ö
区间 ,+¥ 内单调递增.
ç ÷
è 6 ø
因为曲线y = f(x)在点P(x , f(x ))(i=1,2,3)处的切线相互平行,从而x ,x ,x 互不相等,且
1 1 1 1 2 3
f '(x )= f '(x )= f '(x ). 不防设x <0<x <x ,由
1 2 3 1 2 3
3x2 -(a+5) =3x 2 -(a+3)x +a =3x 2 -(a+3)x +a,
1 2 2 3 3
a+3 a+3
可得3x 2 -3x 2 -(a+3)(x -x )=0,解得x +x = ,从而0<x < <x .
2 3 2 3 2 3 3 2 6 3
æa+3ö
设g(x) =3x2 -(a+3)x+a,则g <g(x )<g(0)=a.
ç ÷
è 6 ø 2
2a+5 2a+5 a+3
由3x2 -(a+5) = g(x )<a,解得- <x <0,所以x +x +x >- + ,
1 2 3 1 1 2 3 3 3
2a+5 3t2 -5 é 3 15ù
设t = ,则a = ,因为aÎ-2,0,所以tÎê , ú ,故x +x +x >
3 2 3 3 1 2 3
ë û
3t2 +1 1 1 1
-t + = (t -1)2 - ³ - ,
6 2 3 3
1
即x +x +x >- .
1 2 3 3
第10页 | 共10页