2013年高考数学试卷（文）（安徽）（解析卷）_数学历年高考真题_新·PDF版2008-2025·高考数学真题_数学（按省份分类）2008-2025_2012-2025·（安徽）数学高考真题

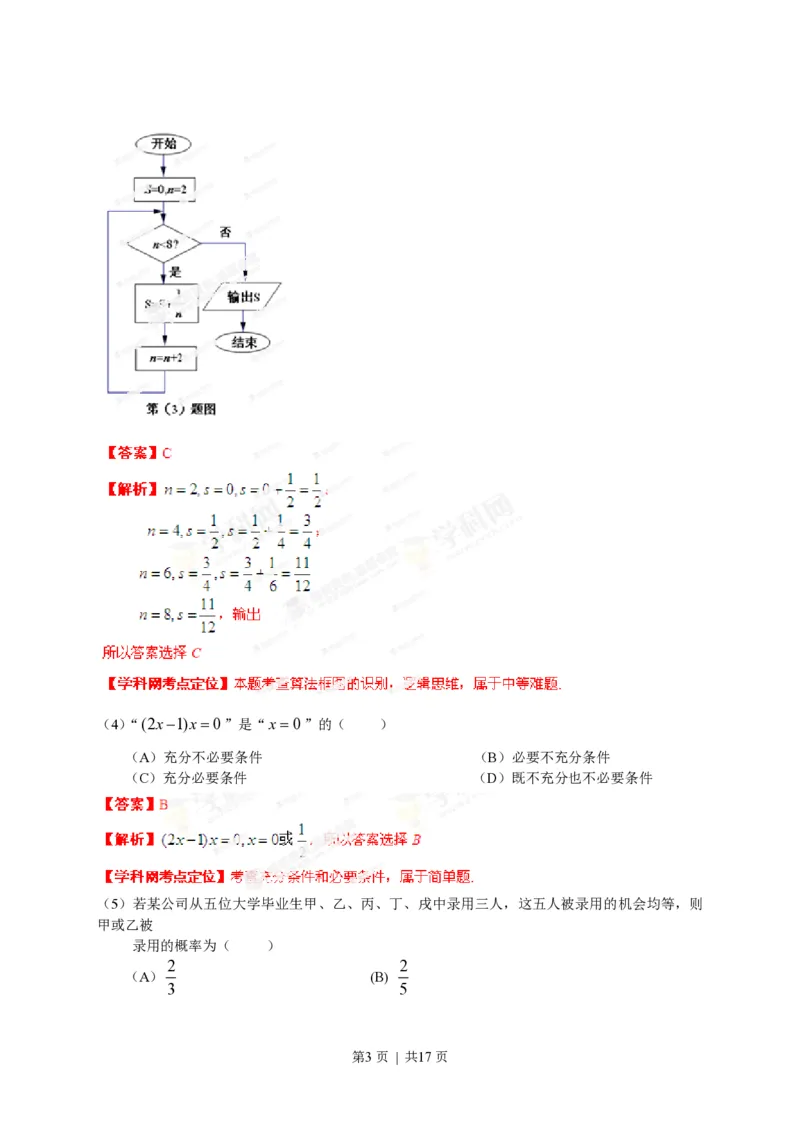
本解析为学科网名师解析团队原创，授权学科网独家使用，如有盗用，依法追责！ 一．选择题选择题：本大题共 10 小题。每小题 5 分，共 50 分。在每个小题给出的四 个选项中，只有一项是符合题目要求的。 第1页 | 共17页10 （1）设i是虚数单位，若复数a (aR)是纯虚数，则a的值为 （ ） 3i （A）-3 （B）-1 （C）1 （D）3 （2）已知Ax|x10,B2,1,0,1，则(C A)B （ ） R （A）2,1 （B）2 （C）1,0,1 （D）0,1 （3）如图所示，程序据图（算法流程图）的输出结果为（ ） 3 1 （A） （B） 4 6 11 25 （C） （D） 12 24 第2页 | 共17页（4）“(2x1)x0”是“x0”的（ ） （A）充分不必要条件 （B）必要不充分条件 （C）充分必要条件 （D）既不充分也不必要条件 （5）若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人，这五人被录用的机会均等，则 甲或乙被 录用的概率为（ ） 2 2 （A） (B) 3 5 第3页 | 共17页3 9 (C) （D） 5 10 （6）直线x2y5 5 0被圆x2  y2 2x4y 0截得的弦长为（ ） （A）1 （B）2 （C）4 （D）4 6 （7）设S 为等差数列a 的前n项和 ，S 4a ,a 2，则a =（ ） n n 8 3 7 9 （A）6 （B）4 （C）2 （D）2 (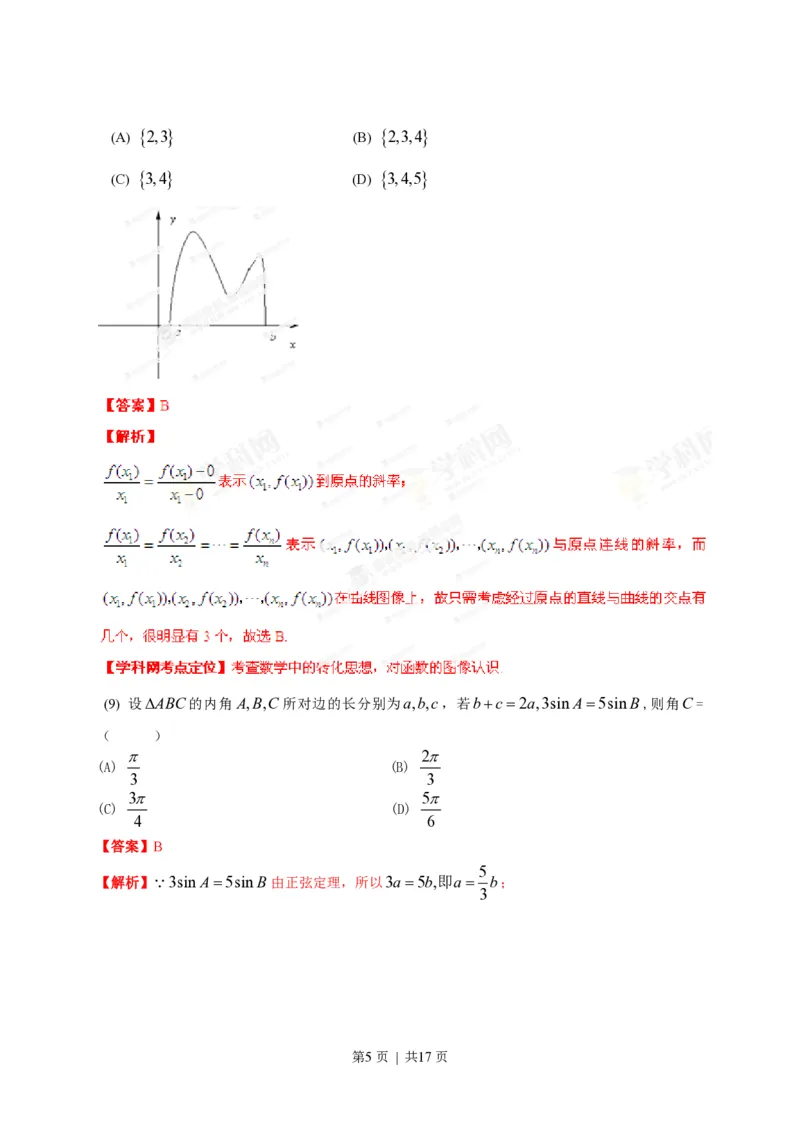8) 函数 y  f(x)的图像如图所示，在区间a,b上可找到n(n2)个不同的数x ,x , ,x 使得 1 2  n， f(x ) f(x ) f(x ) 1  2   n ，则n的取值范围为（ ）  x x x 1 2 n 第4页 | 共17页(A) 2,3 (B) 2,3,4 (C) 3,4 (D) 3,4,5 (9) 设ABC的内角 A,B,C所对边的长分别为a,b,c，若bc2a,3sin A5sinB,则角C= （ ）  2 (A) (B) 3 3 3 5 (C) (D) 4 6 【答案】B 5 【解析】 3sin A5sinB由正弦定理，所以3a5b,即a b；  3 第5页 | 共17页（10）.已知函数 f(x) x3ax2 bxc有两个极值点x ,x ，若 f(x ) x  x ，则关于x的方 1 2 1 1 2 程（ ） 3(f(x))2 2af(x)b0的不同实根个数为 （A）3 (B) 4 (C) 5 (D) 6 （本解析为学科网名师解析团队原创，授权学科网独家使用，如有盗用，依法追责！） 二．填空题 第6页 | 共17页1 （11） 函数y ln(1 ) 1x2 的定义域为_____________. x x y1 （12）若非负数变量x,y满足约束条件 ，则x y的最大值为__________. x2y4         （13）若非零向量a,b满足 a 3b  a2b ，则a,b夹角的余弦值为_______. 第7页 | 共17页（14）定义在R上的函数 f(x)满足 f(x1)2f(x).若当0 x1时。 f(x) x(1x)， 则当1 x0时， f(x)=________________. （15）如图，正方体ABCDABC D 的棱长为1，P为BC的中点，Q为线段CC 上的动点， 1 1 1 1 1 过点A,P,Q的平面截该正方体所得的截面记为S，则下列命题正确的是 （写出所有正 确命题的编号）。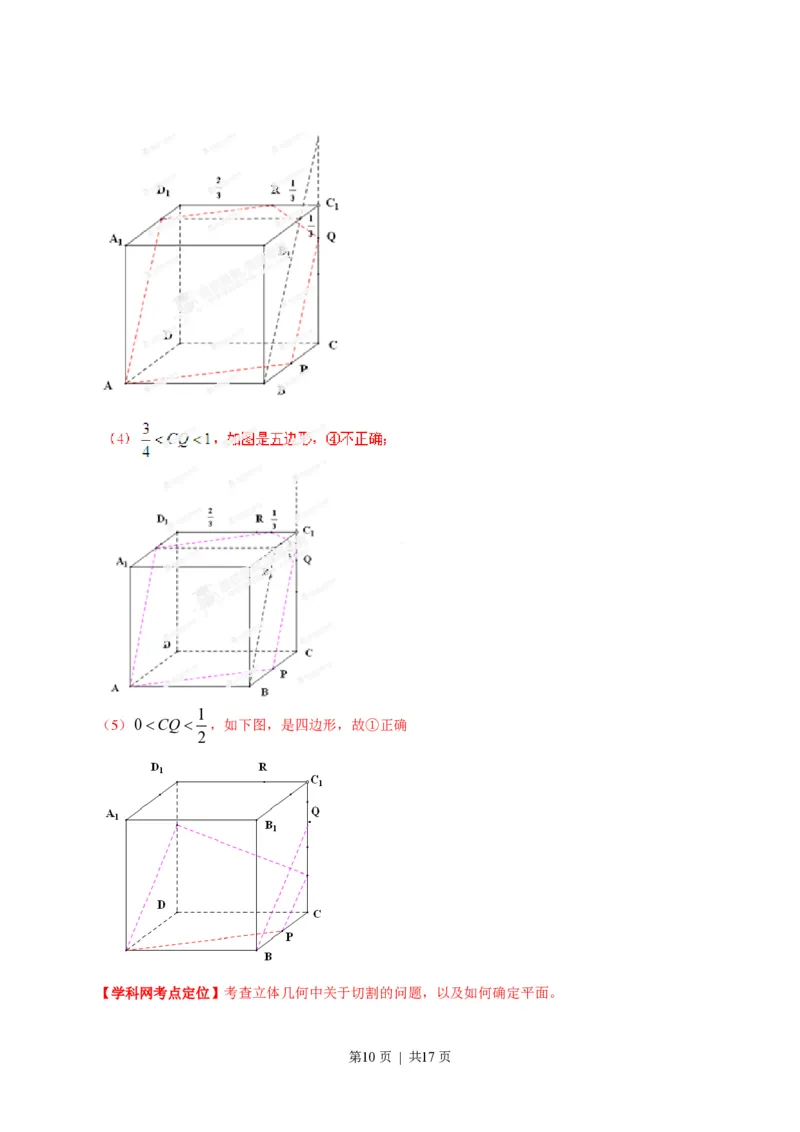 1 ①当0CQ 时，S为四边形 2 1 ②当CQ 时，S为等腰梯形 2 第8页 | 共17页3 1 ③当CQ 时，S与C D 的交点R满足C R 4 1 1 1 3 3 ④当 CQ1时，S为六边形 4 6 ⑤当CQ1时，S的面积为 2 第9页 | 共17页1 （5）0CQ ，如下图，是四边形，故①正确 2 【学科网考点定位】考查立体几何中关于切割的问题，以及如何确定平面。 第10页 | 共17页（本解析为学科网名师解析团队原创，授权学科网独家使用，如有盗用，依法追责！） 三．解答题 （16）（本小题满分12分）  设函数 f(x)sinxsin(x ) . 3 （Ⅰ）求 f(x)的最小值，并求使 f(x)取得最小值的x的集合； （Ⅱ）不画图，说明函数y  f(x)的图像可由y sinx的图象经过怎样的变化得到. （17）（本小题满分12分） 为调查甲、乙两校高三年级学生某次联考数学成绩情况，用简单随机抽样，从这两校中各抽取 30名高三年级学生，以他们的数学成绩（百分制）作为样本，样本数据的茎叶图如下： 第11页 | 共17页甲 乙 7 4 5 5 3 3 2 5 3 3 8 5 5 4 3 3 3 1 0 0 6 0 6 9 1 1 2 2 3 3 5 8 6 6 2 2 1 1 0 0 7 0 0 2 2 2 3 3 6 6 9 7 5 4 4 2 8 1 1 5 5 8 2 0 9 0 （Ⅰ）若甲校高三年级每位学生被抽取的概率为0.05，求甲校高三年级学生总人数，并估计甲校高 三年级这次联考数学成绩的及格率（60分及60分以上为及格）； （Ⅱ）设甲、乙两校高三年级学生这次联考数学平均成绩分别为x ,x ，估计x x 的值. 1 2 1 2 （18）（本小题满分12分） 如 图 ， 四 棱 锥 PABCD的 底 面 ABCD是 边 长 为 2 的 菱 形 ， BAD60. 已 知 PB PD2,PA 6 . （Ⅰ）证明：PC  BD 第12页 | 共17页（Ⅱ）若E为PA的中点，求三菱锥PBCE的体积. 【解析】（1）证明线线垂直，需要线面垂直证起；（2）PAC的面积是PEC 的面积的2倍，BD 是B点到面PEC 的高，求出面积和高，即能求出最终的体积. 【学科网考点定位】考查空间直线与直线，直线与平面的位置，.三棱锥体积等基础知识和基本技能， 考查空间观念，推理论证能力和运算能力. （19）（本小题满分13分） 设数列a 满足a 2，a a 8,且对任意nN*，函数 n 1 2 4 第13页 | 共17页 f(x)(a a a )xa ×cosx-a ×sinx 满足 f '( )0 n n1 n2 n1 n2 2 (Ⅰ)求数列a 的通项公式； n 1 （Ⅱ）若b （2 a  ），求数列b 的前n项和S . n n 2a n n n 、 1 =（n n3）1- 2n 1 n2 3n1- 2n  【解析】第（1）题，通过求导以及 f '( )0，能够判断出a 是等差数列是等差数列，由第 2 n （1）题的结论能够写出b 的通项公式，根据b 的特征，选择求和的方法，利用分组求和的方法即 n n 可求出. 【学科网考点定位】考查函数的求导法则和求导公式，等差、等比数列的性质和数列基本量的求解. 并考查逻辑推理能力和运算能力. （20）（本小题满分13分） 第14页 | 共17页设函数 f(x)ax(1a2)x2，其中a 0，区间I x| f(x)0 . （Ⅰ）求I 的长度（注：区间(,)的长度定义为； （Ⅱ）给定常数k0,1，当1k a1k时，求I 长度的最小值. I  I 1 2 第15页 | 共17页（21）（本小题满分13分） x2 y2 已知椭圆C:  1(ab0)的焦距为4，且过点P( 2，3). a2 b2 （Ⅰ）求椭圆C的方程； （Ⅱ）设Q(x ,y )(x y 0)为椭圆C上一点，过点Q作x轴的垂线，垂足为E。取点 0 0 0 0 A(0,2 2),连接AE，过点A作AE的垂线交x轴于点D。点G是点D关于y轴的对称点，作直 线QG，问这样作出的直线QG是否与椭圆C一定有唯一的公共点？并说明理由. 【答案】（1）因为椭圆过点P( 2，3) 2 3   1 且a2 b2 c2 a2 b2 x2 y2  a2 8 b2 4 c2 4 椭圆C的方程是  1 8 4 （2） 第16页 | 共17页第17页 | 共17页