文档内容
一、选择题:本大题共 10小题,每小题 5分,共 50分. 在每小题给出的四个选
项中,只有一项是符合题目要求的.
1.已知全集U ={1,2,3,4,5},集合A={1,2},B={2,3,4},则𝐵∩∁ 𝐴=
𝑈
A.{2} B.{3,4} C.{1,4,5} D.{2,3,4,5}
π x2 y2 y2 x2
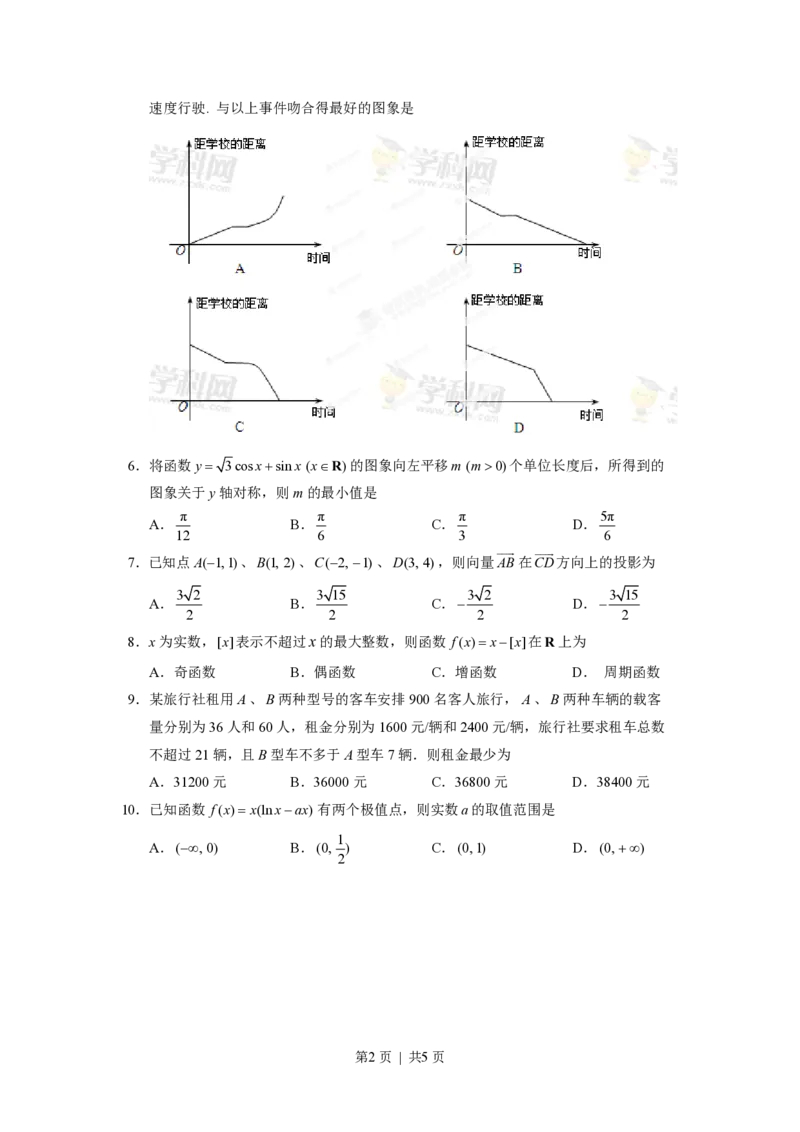
2.已知00)个单位长度后,所得到的
图象关于y轴对称,则m的最小值是
π π π 5π
A. B. C. D.
12 6 3 6
uuur uuur
7.已知点A(-1,1)、B(1, 2)、C(-2, -1)、D(3, 4),则向量AB在CD方向上的投影为
3 2 3 15 3 2 3 15
A. B. C.- D.-
2 2 2 2
8.x为实数,[x]表示不超过x的最大整数,则函数 f(x)=x-[x]在R上为
A.奇函数 B.偶函数 C.增函数 D. 周期函数
9.某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客
量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数
不超过21辆,且B型车不多于A型车7辆.则租金最少为
A.31200元 B.36000元 C.36800元 D.38400元
10.已知函数 f(x)=x(lnx-ax) 有两个极值点,则实数a的取值范围是
1
A.(-¥, 0) B.(0, ) C.(0,1) D.(0, +¥)
2
第2页 | 共5页二、填空题:本大题共 7小题,每小题 5分,共 35分.请将答案填在答题卡对
应题号的位置上. 答错位置,书写不清,模棱两可均不得分.
11.i为虚数单位,设复数z ,z 在复平面内对应的点关于原点对称,若z =2-3i,则
1 2 1
z = .
2
12.某学员在一次射击测试中射靶10次,命中环数如下:
7,8,7,9,5,4,9,10,7,4
则(Ⅰ)平均命中环数为 ;
(Ⅱ)命中环数的标准差为 .
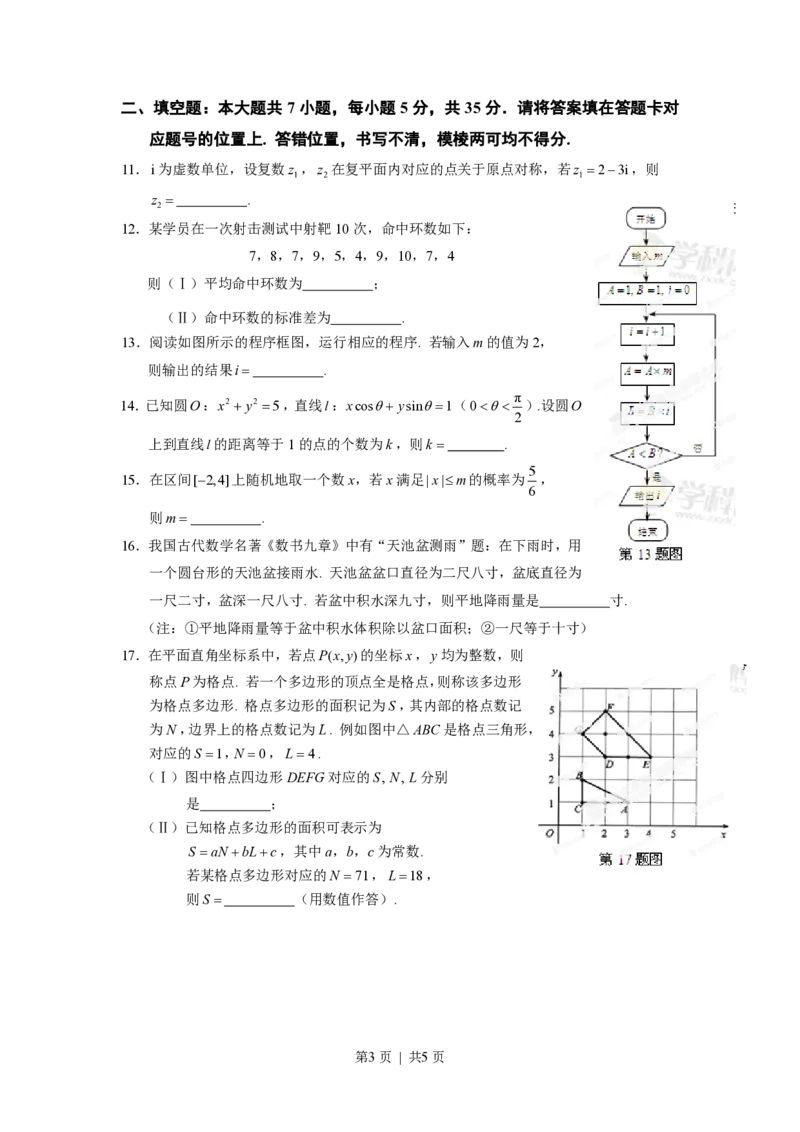
13.阅读如图所示的程序框图,运行相应的程序. 若输入m的值为2,
则输出的结果i= .
π
14.已知圆O:x2 + y2 =5,直线l:xcosq+ ysinq=1(00,b>0,已知函数 f(x)= .
x+1
第4页 | 共5页(Ⅰ)当a¹b时,讨论函数 f(x)的单调性;
(Ⅱ)当x>0时,称 f(x)为a、b关于x的加权平均数.
b b b b
(i)判断 f(1), f( ), f( )是否成等比数列,并证明 f( )£ f( ) ;
a a a a
2ab
(ii)a、b的几何平均数记为G. 称 为a、b的调和平均数,记为H.
a+b
若H £ f(x)£G,求x的取值范围.
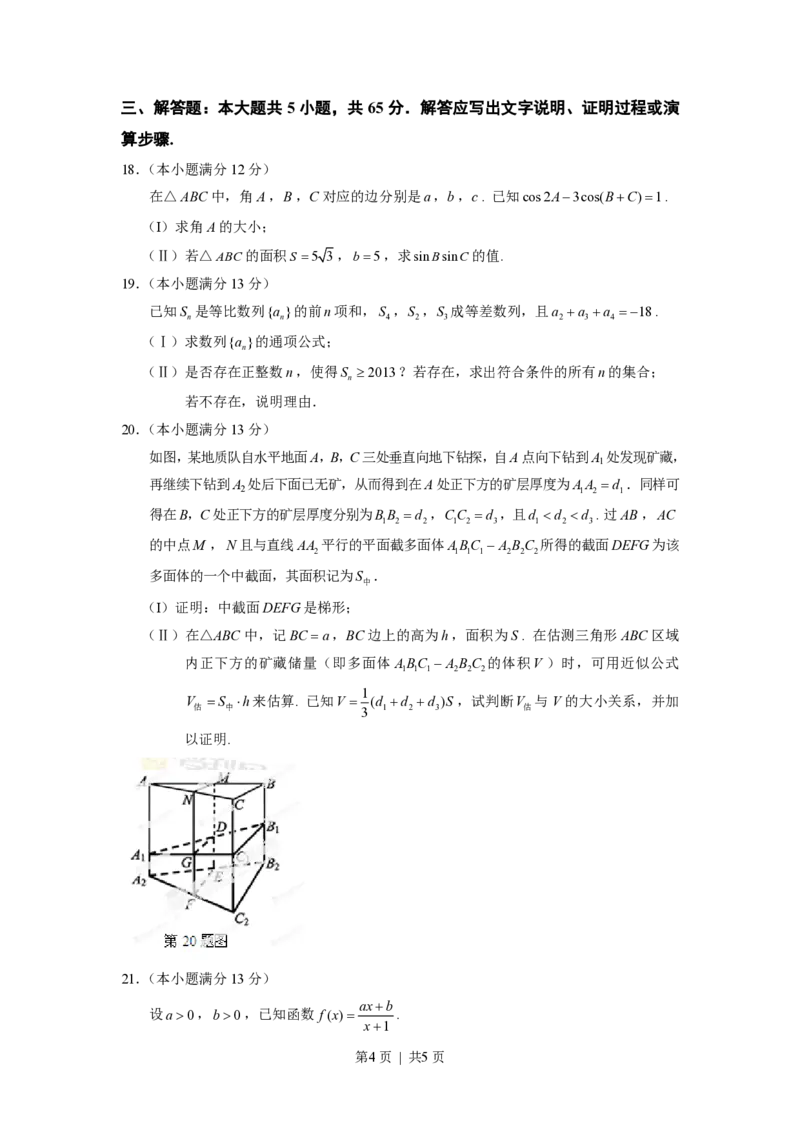
22.(本小题满分14分)
如图,已知椭圆C 与C 的中心在坐标原点O,长轴均为MN 且在x轴上,短轴长分别
1 2
为2m,2n (m>n),过原点且不与x轴重合的直线l与C ,C 的四个交点按纵坐标从
1 2
m
大到小依次为A,B,C,D.记l= ,△BDM 和△ABN 的面积分别为S 和S .
n 1 2
(Ⅰ)当直线l与y轴重合时,若S =lS ,求l的值;
1 2
(Ⅱ)当l变化时,是否存在与坐标轴不重合的直线l,使得S =lS ?并说明理由.
1 2
第5页 | 共5页