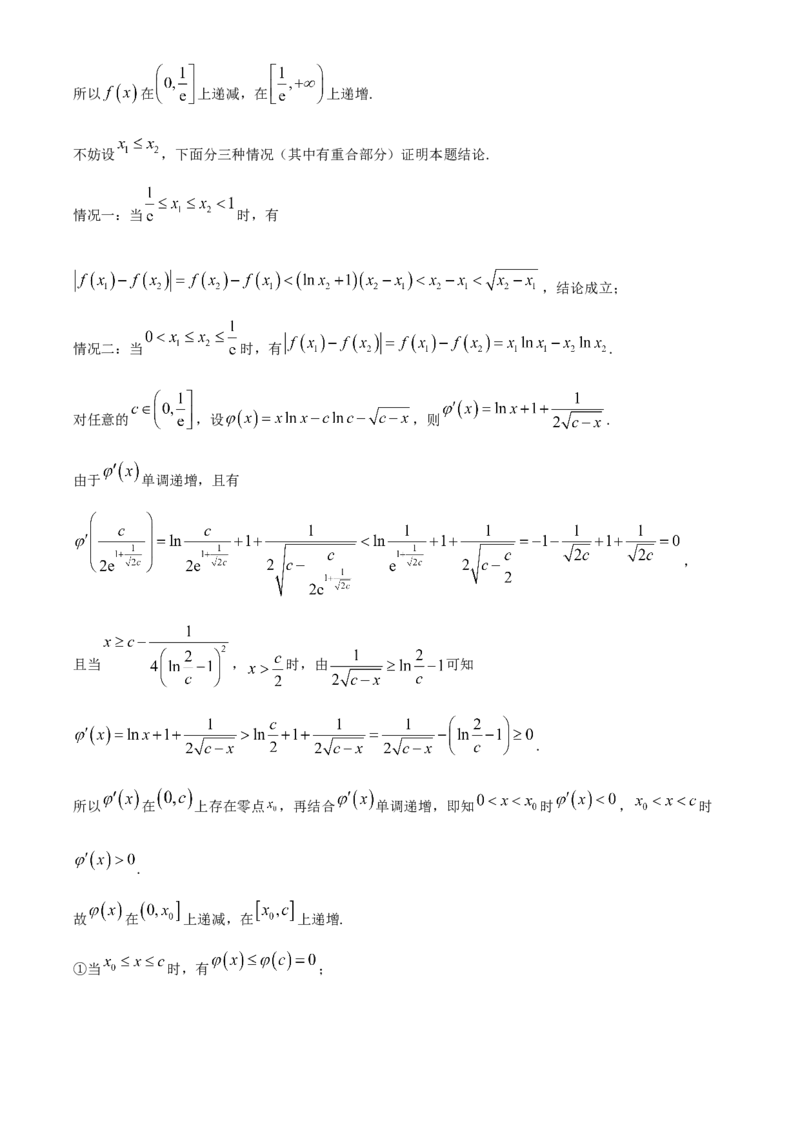文档内容
2024 年普通高等学校招生全国统一考试(天津卷)
数学
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.
第Ⅰ卷1至3页,第Ⅱ卷4至6页.
答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上,并在规定位置
粘贴考试用条形码.答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结
束后,将本试卷和答题卡一并交回.
祝各位考生考试顺利!
第Ⅰ卷(选择题)
注意事项:
1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干
净后,再选涂其他答案标号.
2.本卷共9小题,每小题5分,共45分.
参考公式:
·如果事件 互斥,那么 .
·如果事件 相互独立,那么 .
·球的体积公式 ,其中 表示球的半径.
·圆锥的体积公式 ,其中 表示圆锥的底面面积, 表示圆锥的高.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合 , ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】根据集合交集的概念直接求解即可.【详解】因为集合 , ,
所以 ,
故选:B
2. 设 ,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】
【分析】说明二者与同一个命题等价,再得到二者等价,即是充分必要条件.
【详解】根据立方的性质和指数函数的性质, 和 都当且仅当 ,所以二者互为充要条
件.
故选:C.
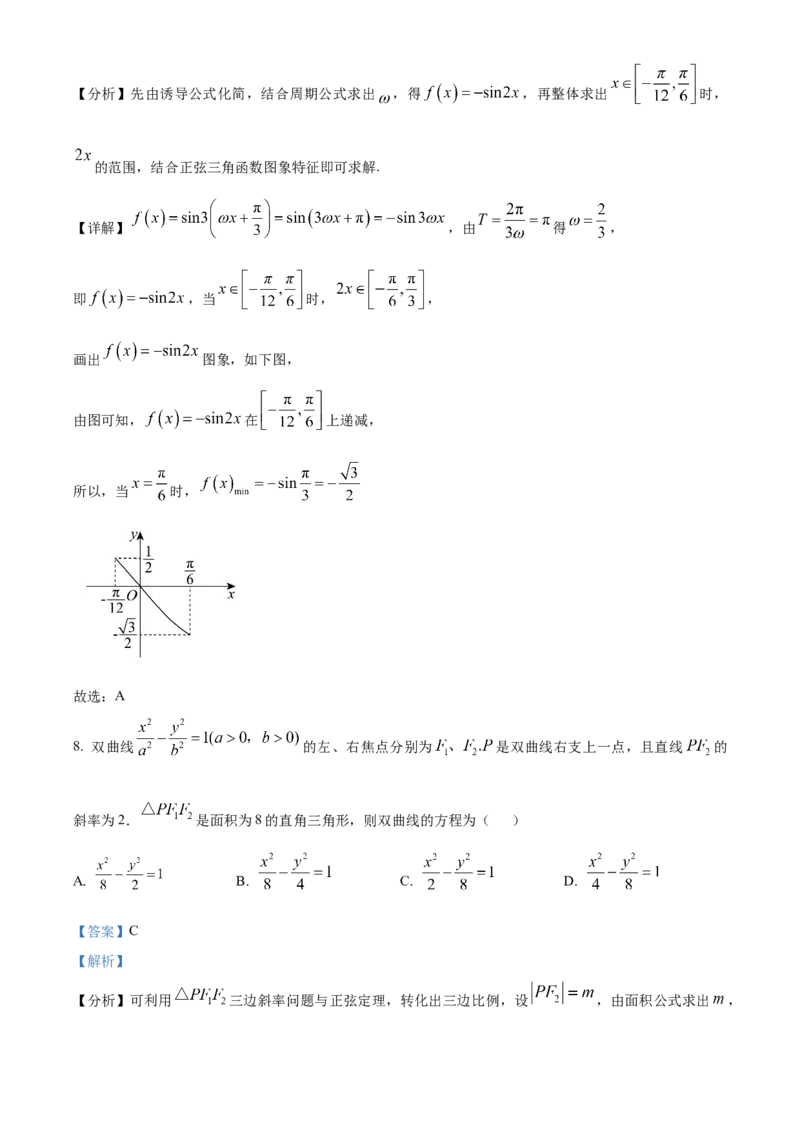
3. 下列图中,线性相关性系数最大的是( )
A. B.
C. D.
【答案】A
【解析】
【分析】由点的分布特征可直接判断
【详解】观察4幅图可知,A图散点分布比较集中,且大体接近某一条直线,线性回归模型拟合效果比较
好,呈现明显的正相关, 值相比于其他3图更接近1.故选:A
4. 下列函数是偶函数的是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据偶函数的判定方法一一判断即可.
【 详 解 】 对 A , 设 , 函 数 定 义 域 为 , 但 , , 则
,故A错误;
对B,设 ,函数定义域为 ,
且 ,则 为偶函数,故B正确;
对C,设 ,函数定义域为 ,不关于原点对称, 则 不是偶函数,故C错误;
对D,设 ,函数定义域为 ,因为 , ,
则 ,则 不是偶函数,故D错误.
故选:B.
5. 若 ,则 的大小关系为( )
A. B. C. D.
【答案】B
【解析】
【分析】利用指数函数和对数函数的单调性分析判断即可.
【详解】因为 在 上递增,且 ,所以 ,
所以 ,即 ,
因为 在 上递增,且 ,
所以 ,即 ,
所以 ,
故选:B
6. 若 为两条不同的直线, 为一个平面,则下列结论中正确的是( )
A. 若 , ,则 B. 若 ,则
.
C 若 ,则 D. 若 ,则 与 相交
【答案】C
【解析】
【分析】根据线面平行的性质可判断AB的正误,根据线面垂直的性质可判断CD的正误.
【详解】对于A,若 , ,则 平行或异面或相交,故A错误.
对于B,若 ,则 平行或异面或相交,故B错误.
对于C, ,过 作平面 ,使得 ,
因为 ,故 ,而 ,故 ,故 ,故C正确.
对于D,若 ,则 与 相交或异面,故D错误.
故选:C.
7. 已知函数 的最小正周期为 .则 在 的最小值是( )
A. B. C. 0 D.
【答案】A
【解析】【分析】先由诱导公式化简,结合周期公式求出 ,得 ,再整体求出 时,
的范围,结合正弦三角函数图象特征即可求解.
【详解】 ,由 得 ,
即 ,当 时, ,
画出 图象,如下图,
由图可知, 在 上递减,
所以,当 时,
故选:A
8. 双曲线 的左、右焦点分别为 是双曲线右支上一点,且直线 的
斜率为2. 是面积为8的直角三角形,则双曲线的方程为( )
A. B. C. D.
【答案】C
【解析】
【分析】可利用 三边斜率问题与正弦定理,转化出三边比例,设 ,由面积公式求出 ,由勾股定理得出 ,结合第一定义再求出 .
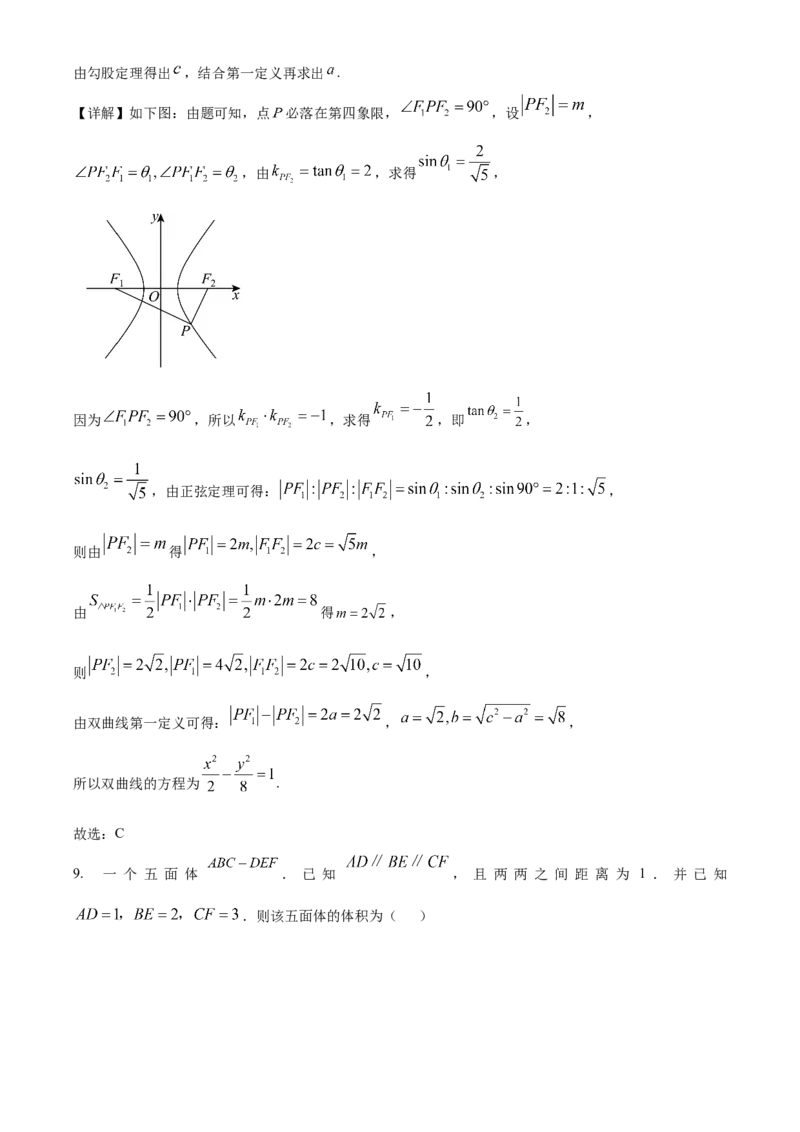
【详解】如下图:由题可知,点 必落在第四象限, ,设 ,
,由 ,求得 ,
因为 ,所以 ,求得 ,即 ,
,由正弦定理可得: ,
则由 得 ,
由 得 ,
则 ,
由双曲线第一定义可得: , ,
所以双曲线的方程为 .
故选:C
9. 一 个 五 面 体 . 已 知 , 且 两 两 之 间 距 离 为 1 . 并 已 知
.则该五面体的体积为( )A. B. C. D.
【答案】C
【解析】
【分析】采用补形法,补成一个棱柱,求出其直截面,再利用体积公式即可.
【详解】用一个完全相同的五面体 (顶点与五面体 一一对应)与该五面体相嵌,
使得 ; ; 重合,
因为 ,且两两之间距离为1. ,
则形成的新组合体为一个三棱柱,
该三棱柱的直截面(与侧棱垂直的截面)为边长为1的等边三角形,侧棱长为 ,
.
故选:C.
第Ⅱ卷
注意事项:
1.用黑色墨水的钢笔或签字笔将答案写在答题卡上.
2.本卷共11小题,共105分.
二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给
3分,全部答对的给5分.10. 已知 是虚数单位,复数 ______.
【答案】
【解析】
【分析】借助复数的乘法运算法则计算即可得.
【详解】 .
故答案为: .
11. 在 的展开式中,常数项为______.
【答案】20
【解析】
【分析】根据题意结合二项展开式的通项分析求解即可.
【详解】因为 的展开式的通项为 ,
令 ,可得 ,
所以常数项为 .
故答案为:20.
12. 圆 的圆心与抛物线 的焦点 重合, 为两曲线的交点,则原点到
直线 的距离为______.
【答案】 ##
【解析】
【分析】先求出圆心坐标,从而可求焦准距,再联立圆和抛物线方程,求 及 的方程,从而可求原点
到直线 的距离.【详解】圆 的圆心为 ,故 即 ,
由 可得 ,故 或 (舍),
故 ,故直线 即 或 ,
故原点到直线 的距离为 ,
故答案为:
13. 五种活动,甲、乙都要选择三个活动参加.甲选到 的概率为______;已知乙选了 活动,
他再选择 活动的概率为______.
【答案】 ①. ②.
【解析】
【分析】结合列举法或组合公式和概率公式可求甲选到 的概率;采用列举法或者条件概率公式可求乙选
了 活动,他再选择 活动的概率.
【详解】解法一:列举法
从五个活动中选三个的情况有:
,共10种情况,
其中甲选到 有6种可能性: ,
则甲选到 得概率为: ;
乙选 活动有6种可能性: ,
其中再选则 有3种可能性: ,故乙选了 活动,他再选择 活动的概率为 .
解法二:
设甲、乙选到 为事件 ,乙选到 为事件 ,
则甲选到 的概率为 ;
乙选了 活动,他再选择 活动的概率为
故答案为: ;
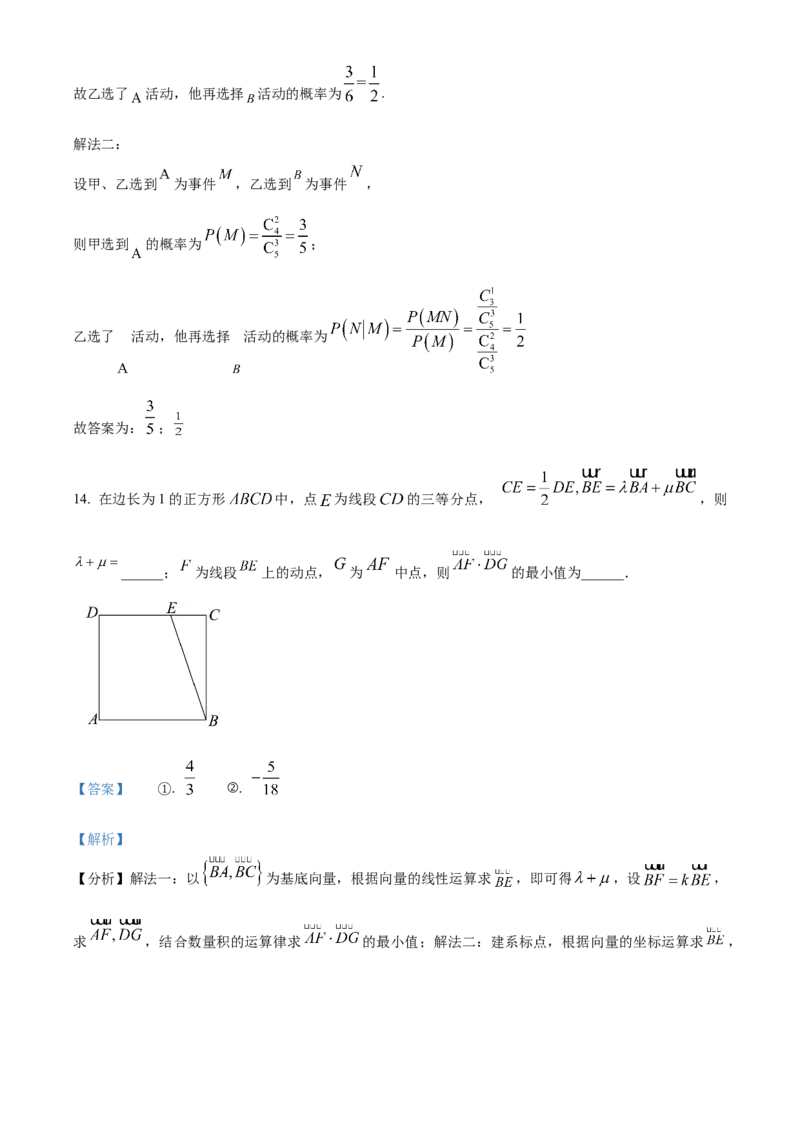
14. 在边长为1的正方形 中,点 为线段 的三等分点, ,则
______; 为线段 上的动点, 为 中点,则 的最小值为______.
【答案】 ①. ②.
【解析】
【分析】解法一:以 为基底向量,根据向量的线性运算求 ,即可得 ,设 ,
求 ,结合数量积的运算律求 的最小值;解法二:建系标点,根据向量的坐标运算求 ,即可得 ,设 ,求 ,结合数量积的坐标运算求 的最小值.
【详解】解法一:因 为,即 ,则 ,
可得 ,所以 ;
由题意可知: ,
因为 为线段 上的动点,设 ,
则 ,
又因为 为 中点,则 ,
可得
,
又因为 ,可知:当 时, 取到最小值 ;
解法二:以B为坐标原点建立平面直角坐标系,如图所示,则 ,
可得 ,
因为 ,则 ,所以 ;
因为点 在线段 上,设 ,
且 为 中点,则 ,
可得 ,
则 ,
且 ,所以当 时, 取到最小值为 ;
故答案为: ; .
15. 若函数 恰有一个零点,则 的取值范围为______.
【答案】
【解析】
【分析】结合函数零点与两函数的交点的关系,构造函数 与 ,则
两函数图象有唯一交点,分 、 与 进行讨论,当 时,计算函数定义域可得 或,计算可得 时,两函数在 轴左侧有一交点,则只需找到当 时,在 轴右侧无交
点的情况即可得;当 时,按同一方式讨论即可得.
【详解】令 ,即 ,
由题可得 ,
当 时, ,有 ,则 ,不符合要求,舍去;
当 时,则 ,
即函数 与函数 有唯一交点,
由 ,可得 或 ,
当 时,则 ,则 ,
即 ,整理得 ,
当 时,即 ,即 ,
当 , 或 (正值舍去),
当 时, 或 ,有两解,舍去,
即当 时, 在 时有唯一解,
则当 时, 在 时需无解,当 ,且 时,
由函数 关于 对称,令 ,可得 或 ,
且函数 在 上单调递减,在 上单调递增,
令 ,即 ,
故 时, 图象为双曲线 右支 轴上方部分向右平移 所得,
的
由 的渐近线方程为 ,
即 部分的渐近线方程为 ,其斜率为 ,
又 ,即 在 时的斜率 ,
令 ,可得 或 (舍去),
且函数 在 上单调递增,
故有 ,解得 ,故 符合要求;当 时,则 ,
即函数 与函数 有唯一交点,
由 ,可得 或 ,
当 时,则 ,则 ,
即 ,整理得 ,
当 时,即 ,即 ,
当 , (负值舍去)或 ,
当 时, 或 ,有两解,舍去,
即当 时, 在 时有唯一解,
则当 时, 在 时需无解,
当 ,且 时,
由函数 关于 对称,令 ,可得 或 ,
且函数 在 上单调递减,在 上单调递增,同理可得: 时, 图象为双曲线 左支的 轴上方部分向左平移 所得,
部分的渐近线方程为 ,其斜率为 ,
又 ,即 在 时的斜率 ,
令 ,可得 或 (舍去),
且函数 在 上单调递减,
故有 ,解得 ,故 符合要求;
综上所述, .
故答案为: .
【点睛】关键点点睛:本题关键点在于将函数 的零点问题转化为函数 与函数
的交点问题,从而可将其分成两个函数研究.
三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤
16. 在 中,角 所对 的边分别为 ,已知 .
(1)求 ;
(2)求 ;(3)求 的值.
【答案】(1)
(2)
(3)
【解析】
【分析】(1) ,利用余弦定理即可得到方程,解出即可;
(2)法一:求出 ,再利用正弦定理即可;法二:利用余弦定理求出 ,则得到 ;
(3)法一:根据大边对大角确定 为锐角,则得到 ,再利用二倍角公式和两角差的余弦公式即可;
法二:直接利用二倍角公式和两角差的余弦公式即可.
【小问1详解】
设 , ,则根据余弦定理得 ,
即 ,解得 (负舍);
则 .
【小问2详解】
法一:因为 为三角形内角,所以 ,
再根据正弦定理得 ,即 ,解得 ,
法二:由余弦定理得 ,
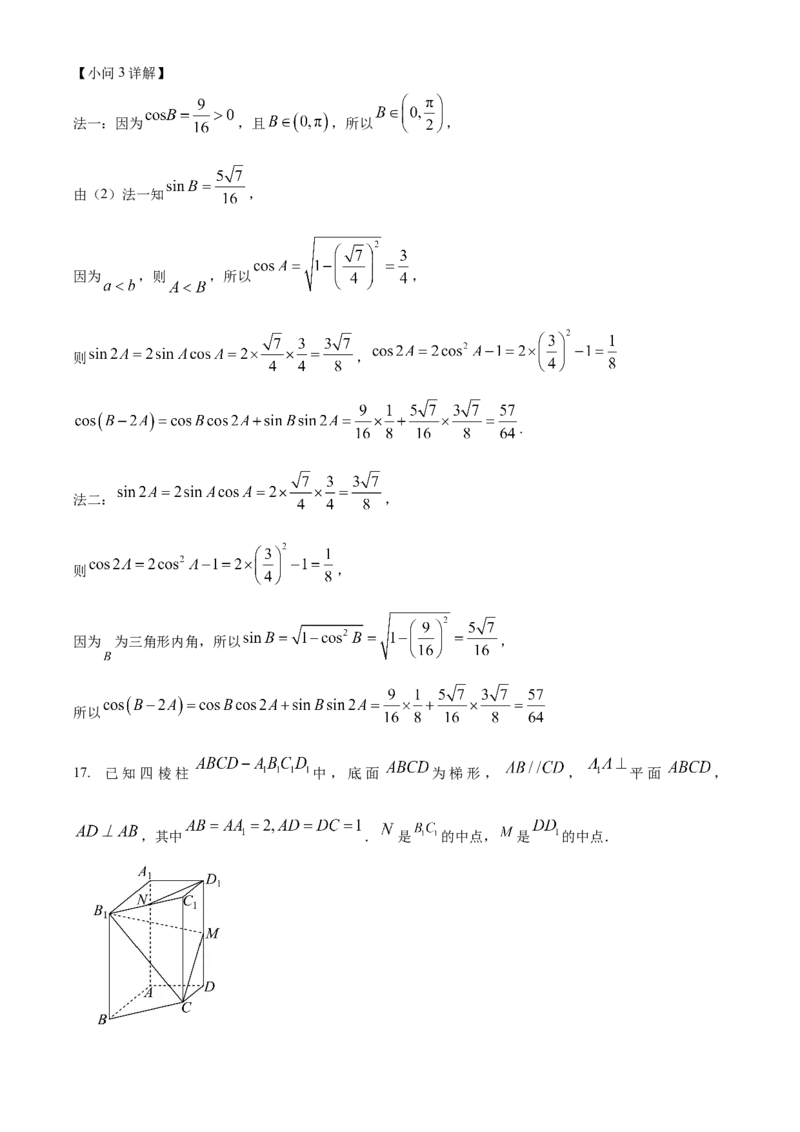
因为 ,则【小问3详解】
法一:因为 ,且 ,所以 ,
由(2)法一知 ,
因为 ,则 ,所以 ,
则 ,
.
法二: ,
则 ,
因为 为三角形内角,所以 ,
所以
17. 已知四棱柱 中,底面 为梯形, , 平面 ,
,其中 . 是 的中点, 是 的中点.(1)求证 平面 ;
(2)求平面 与平面 的夹角余弦值;
(3)求点 到平面 的距离.
【答案】(1)证明见解析
(2)
(3)
【解析】
【分析】(1)取 中点 ,连接 , ,借助中位线的性质与平行四边形性质定理可得 ,
结合线面平行判定定理即可得证;
(2)建立适当空间直角坐标系,计算两平面的空间向量,再利用空间向量夹角公式计算即可得解;
(3)借助空间中点到平面的距离公式计算即可得解.
【小问1详解】
取 中点 ,连接 , ,
由 是 的中点,故 ,且 ,
由 是 的中点,故 ,且 ,
则有 、 ,
故四边形 是平行四边形,故 ,
又 平面 , 平面 ,
故 平面 ;
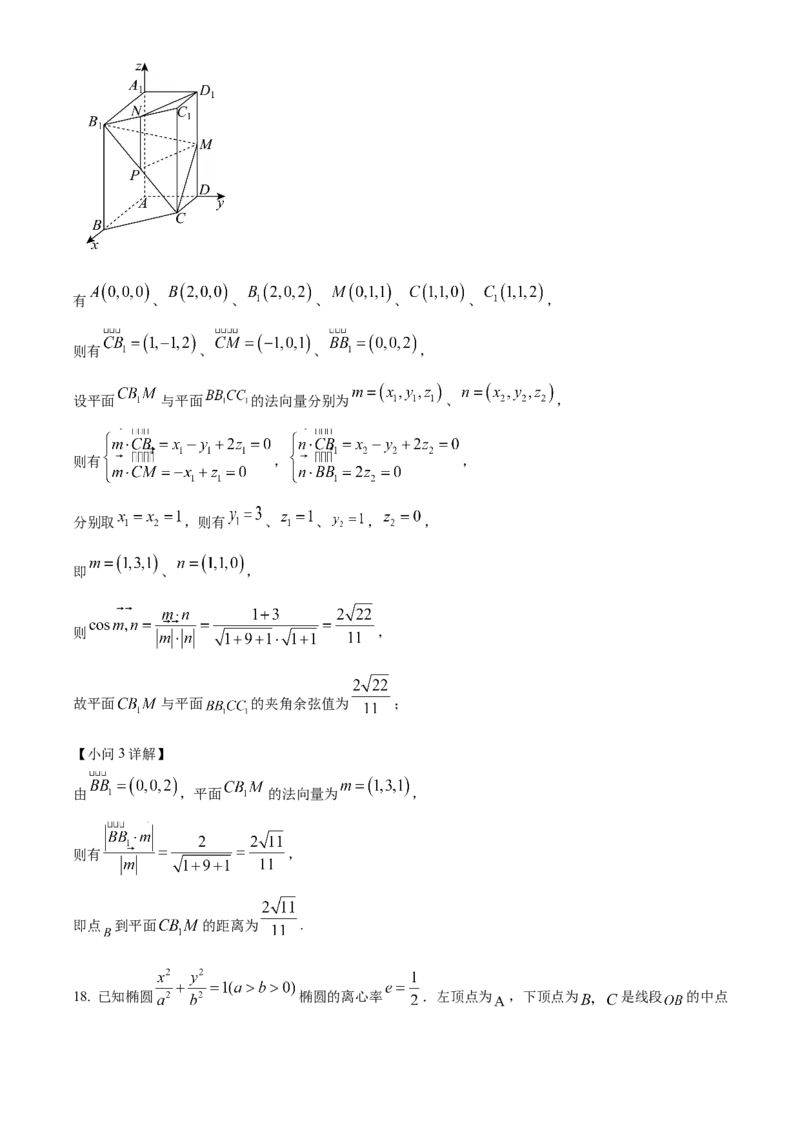
【小问2详解】
以 为原点建立如图所示空间直角坐标系,有 、 、 、 、 、 ,
则有 、 、 ,
设平面 与平面 的法向量分别为 、 ,
则有 , ,
分别取 ,则有 、 、 , ,
即 、 ,
则 ,
故平面 与平面 的夹角余弦值为 ;
【小问3详解】
由 ,平面 的法向量为 ,
则有 ,
即点 到平面 的距离为 .
18. 已知椭圆 椭圆的离心率 .左顶点为 ,下顶点为 是线段 的中点其中 .
(1)求椭圆方程.
(2)过点 的动直线与椭圆有两个交点 .在 轴上是否存在点 使得 .若存在
求出这个 点纵坐标的取值范围,若不存在请说明理由.
【答案】(1)
(2)存在 ,使得 恒成立.
【解析】
的
【分析】(1)根据椭圆 离心率和三角形的面积可求基本量,从而可得椭圆的标准方程.
(2)设该直线方程为: , , 联立直线方程和椭圆方程并消元,
结合韦达定理和向量数量积的坐标运算可用 表示 ,再根据 可求 的范围.
【小问1详解】
因为椭圆的离心率为 ,故 , ,其中 为半焦距,
所以 ,故 ,
故 ,所以 , ,故椭圆方程为: .
【小问2详解】若过点 的动直线的斜率存在,则可设该直线方程为: ,
设 ,
由 可得 ,
故 且
而 ,
故
,
因为 恒成立,故 ,解得 .若过点 的动直线的斜率不存在,则 或 ,
此时需 ,两者结合可得 .
综上,存在 ,使得 恒成立.
【点睛】思路点睛:圆锥曲线中的范围问题,往往需要用合适的参数表示目标代数式,表示过程中需要借
助韦达定理,此时注意直线方程的合理假设.
19. 已知数列 是公比大于0的等比数列.其前 项和为 .若 .
(1)求数列 前 项和 ;
(2)设 , .
(ⅰ)当 时,求证: ;
(ⅱ)求 .
【答案】(1)
(2)①证明见详解;②
【解析】
【分析】(1)设等比数列 的公比为 ,根据题意结合等比数列通项公式求 ,再结合等比数列
求和公式分析求解;
(2)①根据题意分析可知 , ,利用作差法分析证明;②根据题意结合
等差数列求和公式可得 ,再结合裂项相消法分析求解.
【小问1详解】设等比数列 的公比为 ,
因为 ,即 ,
可得 ,整理得 ,解得 或 (舍去),
所以 .
【小问2详解】
(i)由(1)可知 ,且 ,
当 时,则 ,即
可知 ,
,
可得 ,
当且仅当 时,等号成立,
所以 ;
(ii)由(1)可知: ,
若 ,则 ;
若 ,则 ,
当 时, ,可知 为等差数列,
可得 ,
所以 ,且 ,符合上式,综上所述: .
【点睛】关键点点睛:1.分析可知当 时, ,可知 为等差数列;
2.根据等差数列求和分析可得 .
20. 设函数 .
(1)求 图象上点 处的切线方程;
(2)若 在 时恒成立,求 的值;
(3)若 ,证明 .
【答案】(1)
(2)2 (3)证明过程见解析
【解析】
【分析】(1)直接使用导数的几何意义;
(2)先由题设条件得到 ,再证明 时条件满足;
(3)先确定 的单调性,再对 分类讨论.
【小问1详解】
由于 ,故 .
所以 , ,所以所求的切线经过 ,且斜率为 ,故其方程为 .
【小问2详解】
设 ,则 ,从而当 时 ,当 时 .
所以 在 上递减,在 上递增,这就说明 ,即 ,且等号成立当且仅
当 .设 ,则
.
当 时, 的取值范围是 ,所以命题等价于对任意 ,都有 .
一方面,若对任意 ,都有 ,则对 有
,
取 ,得 ,故 .
再取 ,得 ,所以 .
另一方面,若 ,则对任意 都有 ,满足条件.
综合以上两个方面,知 的值是2.
【小问3详解】
先证明一个结论:对 ,有 .
证明:前面已经证明不等式 ,故 ,
且 ,
所以 ,即 .
由 ,可知当 时 ,当 时 .所以 在 上递减,在 上递增.
不妨设 ,下面分三种情况(其中有重合部分)证明本题结论.
情况一:当 时,有
,结论成立;
情况二:当 时,有 .
对任意的 ,设 ,则 .
由于 单调递增,且有
,
且当 , 时,由 可知
.
所以 在 上存在零点 ,再结合 单调递增,即知 时 , 时
.
故 在 上递减,在 上递增.
①当 时,有 ;②当 时,由于 ,故我们可以取 .
从而当 时,由 ,可得
.
再根据 在 上递减,即知对 都有 ;
综合①②可知对任意 ,都有 ,即 .
根据 和 的任意性,取 , ,就得到 .
所以 .
情况三:当 时,根据情况一和情况二的讨论,可得
, .
而根据 的单调性,知 或 .
故一定有 成立.
综上,结论成立.
【点睛】关键点点睛:本题的关键在于第3小问中,需要结合 的单调性进行分类讨论.