2024届广东省四校高三第一次联考数学答案(1)_2023年8月_028月合集_2024届广东省四校（深中、华附、省实、广雅）高三上学期第一次联考

参考答案： 1．D 【解析】由题意， yln(1x2)ln10，故M ,0  ，故 ð M  N (0,)(1,1)(1,) R 2．A 1 1i 1 1 【解析】由复数  1i  z 1，可得z   ，对应的点为 , ，在第一象限. 1i 2 2 2 故选：A. 3．A 【分析】先由不等式恒成立求出m的取值范围，再根据充分条件和必要条件的定义分析判断. 【详解】由x2mx10在x1,上恒成立，得 m x 1 在x1,上恒成立， x 1 令 f(x)x ，由对勾函数的性质可知 f(x)在x1,上单调递增， x 所以 f(x) f(1)2， 所以m2， 所以“x2mx10在x1,上恒成立”的充要条件为m2， 所以“m1”是“x2mx10在x1,上恒成立”的充分不必要条件， 故选：A 4．C 【分析】建立平面直角坐标系，利用数量积及模的坐标运算求解即可. 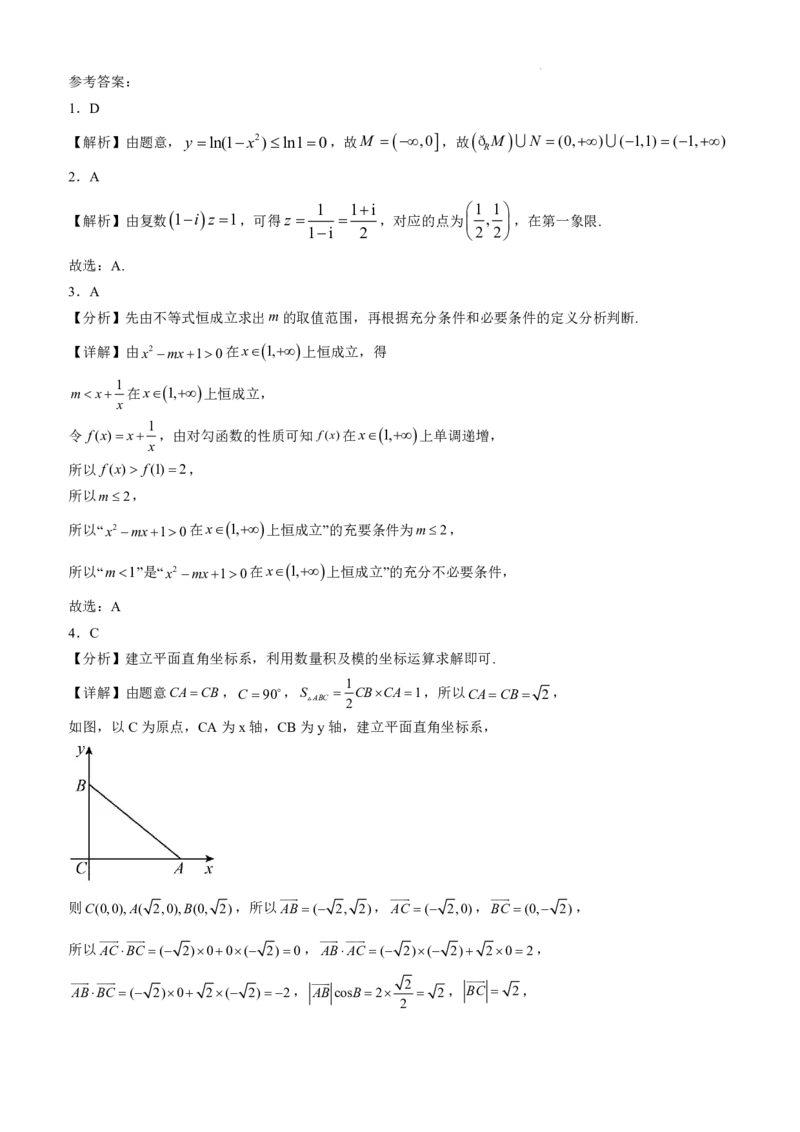1 【详解】由题意CACB，C 90，S  CBCA1，所以CACB 2， ABC 2 如图，以C为原点，CA为x轴，CB为y轴，建立平面直角坐标系，    则C(0,0),A( 2,0),B(0, 2)，所以AB( 2, 2)，AC ( 2,0)，BC (0, 2)，     所以ACBC ( 2)00( 2)0，ABAC ( 2)( 2) 202，    2  ABBC ( 2)0 2( 2)2， AB cosB2  2， BC  2， 2  所以 AB cosB BC ，所以选项ABD正确，C错误. 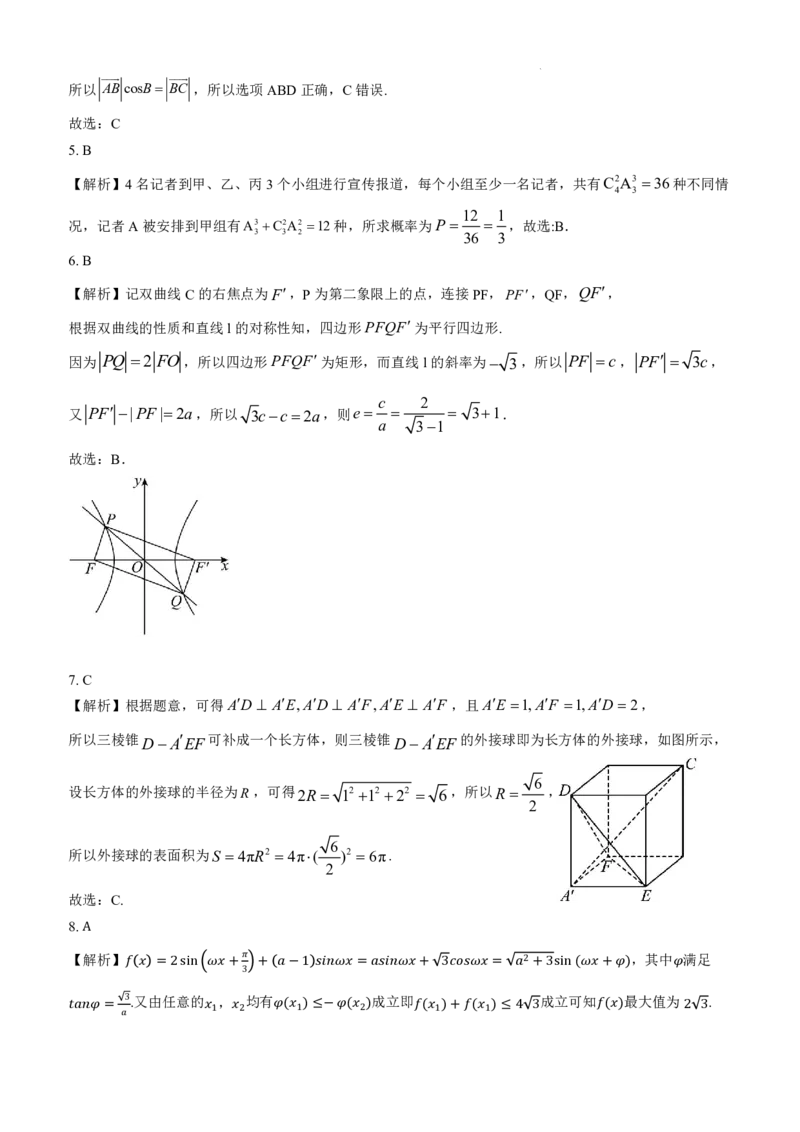故选：C 5.B 【解析】4名记者到甲、乙、丙3个小组进行宣传报道，每个小组至少一名记者，共有C2A3 36种不同情 4 3 12 1 况，记者A被安排到甲组有A3 C2A2 12种，所求概率为P   ，故选:B． 3 3 2 36 3 6.B 【解析】记双曲线C的右焦点为F，P为第二象限上的点，连接PF，PF，QF，QF， 根据双曲线的性质和直线l的对称性知，四边形PFQF为平行四边形. 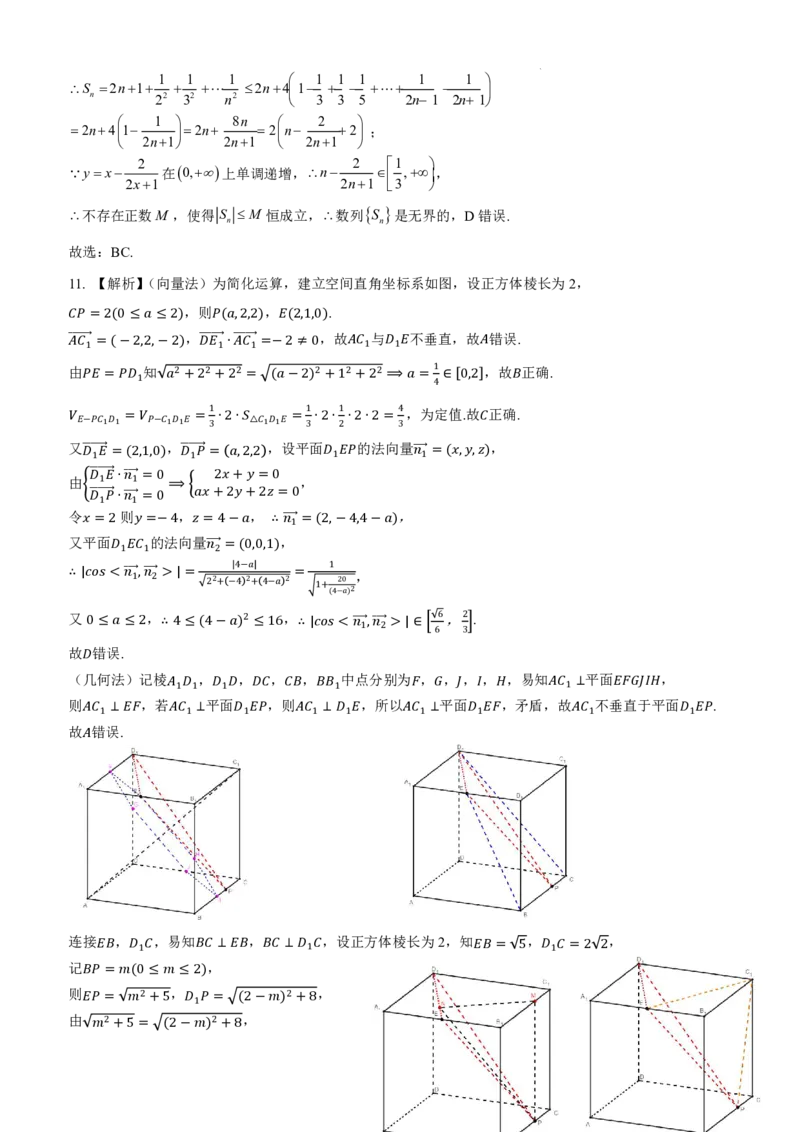因为 PQ 2 FO ，所以四边形PFQF为矩形，而直线l的斜率为 3，所以 PF c， PF  3c， c 2 又 PF |PF |2a，所以 3cc2a，则e   31． a 31 故选：B． 7.C 【解析】根据题意，可得AD  AE,AD  AF,AE  AF ，且AE 1,AF 1,AD  2， 所以三棱锥 D A  EF 可补成一个长方体，则三棱锥 D A  EF 的外接球即为长方体的外接球，如图所示， 6 设长方体的外接球的半径为R，可得2R 12 12 22  6，所以R  ， 2 6 所以外接球的表面积为S 4πR2  4π( )2  6π. 2 故选：C. 8. 【解A 析】 ，其中 满足 2 =2sin +3 + −1 = + 3 = +3sin ( + ) .又由任意的 ， 均有 成立即 成立可知 最大值为 . 3 = 1 2 ( 1)≤− ( 2) ( 1)+ ( 1)≤ 4 3 ( ) 2 3 学科网（北京）股份有限公司，又 ， ， ，又 知 ，又 2 ∴ +3 =2 3 >0 ∴ =3 ∴ =2sin ( +6) 0< < 6 < +6 ≤ +6 ( ) 在 上存在唯一实数 使 即 ， ， . 1 7 11 5 选 0., 0 0 =− 3 sin 0+6 =−2 ∴ 6 < +6 ≤ 6 ∴1< ≤3 9. A【答案】ACD 【详解】对选项A：将一组数据中的每个数据都加上同一个常数后，方差不变，正确； 1 对选项B：E(x)np30，D(x)np1 p20，解得p ，错误； 3 1 1 对选项C：根据正态分布的对称性知，P(0) ，P(1) p，则P(10)P(01)  p，正 2 2 确； 对选项D：X ~B(10,0.8)，故 pX nCn 0.8n 10.810n， 10 pX n pX n1 Cn 0.8n0.210n Cn10.8n10.211n 39 44  ，即 10 10 ，解得 n ，故n8，D正确. pX n pX n1 Cn 0.8n0.210n Cn10.8n10.29n 5 5 10 10 故选：ACD 10. 【答案】BC 1 1 【解析】对于A，a   1恒成立，存在正数M 1，使得 a M 恒成立， n n n n 数列a 是有界的，A错误； n n n n 1 1 1 对于B，1sinn1    a    sinn   ， 2 n 2 2 2 n n 1 1 1 1 S a a a        1   1， n 1 2 n 2 2 2 2  2 n n 1 1 1 1 S a a a        1   1， n 1 2 n  2 2 2  2 所以存在正数M 1，使得 S M 恒成立， 则数列  S  是有界的，B正确； n n 对于C，当n为偶数时，S 0；当n为奇数时，S 1； n n S 1，存在正数M 1，使得 S M 恒成立， n n 数列S 是有界的，C正确； n 1 4 4  1 1  对于D，    4  ， n2 4n2  2n1  2n1  2n1 2n1 学科网（北京）股份有限公司1 1 1  1 1 1 1 1  S 2n1   2n41      n 22 32 n2  3 3 5 2n 1 2n 1  1  8n  2  2n41 2n 2n 2 ；  2n1 2n1  2n1  2 2 1  yx 在0,上单调递增，n   ,， 2x1 2n1 3  不存在正数M ，使得 S M 恒成立，数列S 是无界的，D错误. n n 故选：BC. 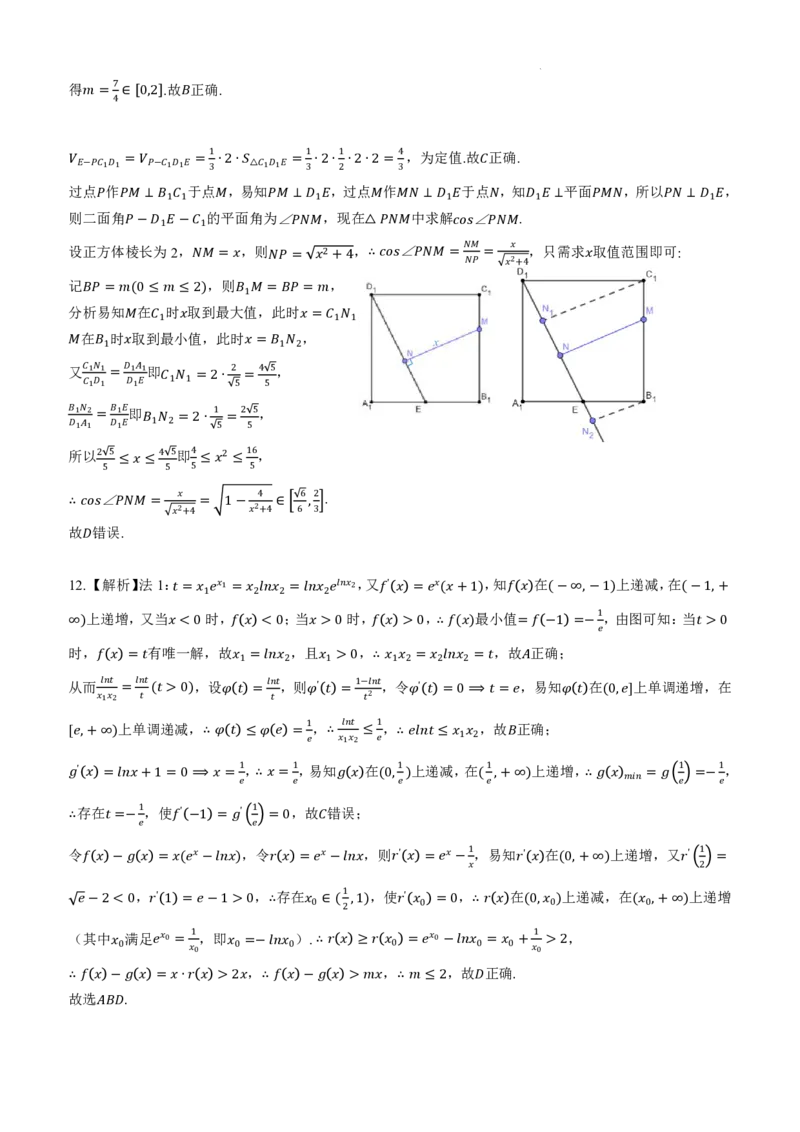11. 【解析】（向量法）为简化运算，建立空间直角坐标系如图，设正方体棱长为2， ，则 ， . =2(0 ≤ ≤ 2) ， ( ,2,2) (2,1,0 ， ) 故 与 不垂直，故 错误. 由 1=(−2,知2,−2) 1∙ 1=−2≠0 1 1 ，故 正确. 2 2 2 2 2 2 1 = 1 +2 +2 = ( −2) +1 +2 ⟹ =4∈ 0,2 ，为定值.故 正确. 1 1 1 4 又 − 1 1 = − ， 1 1 =3∙2∙ △ 1 ， 1 设=平3面∙2∙2∙2的∙法2=向3量 ， 由 1 =(2,1,0) 1 = ,2,2 ， 1 1=( , , ) 1 ∙ 1=0 2 + =0 令 则 ⟹， ， ， 1 ∙ 1=0 +2 +2 =0 又平 = 面 2 = 的 − 法 4 向 量 =4− ∴ ， 1=(2,−4,4− ) 1 1 2=(0,0,1) ， 4− 1 ∴ | < 1, 2>|= 2 2 + −4 2 + 4− 2 = 1+(4− 20 )2 又 ， ， ， . 2 6 2 故0错≤误 .≤2 ∴ 4≤(4− ) ≤16 ∴ | < 1, 2>| ∈ 6 3 （几何法）记棱 ， ， ， ， 中点分别为 ， ， ， ， ，易知 平面 ， 则 ，若 1 1 平 面 1 ，则 1 ，所以 平面 ，矛盾， 故 1 ⊥ 不垂 直 于 平面 . 故 错1误 ⊥. 1 ⊥ 1 1 ⊥ 1 1 ⊥ 1 1 1 连接 ， ，易知 ， ，设正方体棱长为2，知 ， ， 记 1 ， ⊥ ⊥ 1 = 5 1 =2 2 则 ， ， = (0≤ ≤ 2) 由 2 ， 2 = +5 1 = (2− ) +8 2 2 +5 = (2− ) +8 学科网（北京）股份有限公司得 .故 正确. 7 =4∈ 0,2 ，为定值.故 正确. 1 1 1 4 过 点 − 1 作 1 = − 1 1 于=点3∙2，∙易 △ 知 1 1 =3∙2，∙2过∙2点∙2作=3 于点 ，知 平面 ，所以 ， 则二面 角 ⊥ 1 1 的 平面角为 ∠ ⊥ 1 ，现在 中 ⊥ 求 解1 ∠ . 1 ⊥ ⊥ 1 设正方体棱 −长 为 1 2，− 1 ，则 ，△ ∠ ，只需求 取值范围即可: 2 记 ，=则 = ，+4 ∴ = = 2 +4 分析 易 = 知 (0 在 ≤ 时 ≤ 取 2 到 ) 最大 值1 ， = 此 时 = ， 在 时 取到 1最小 值，此时 ， = 1 1 x 又 1 即 = ， 1 2 1 1 1 1 2 4 5 1 1 = 1 1 1 =2∙ 5= 5 即 ， 1 2 1 1 2 5 1 1 = 1 1 2 =2∙ 5= 5 所以 即 ， 2 5 4 5 4 2 16 5 ≤ ≤ 5 5≤ ≤ 5 ∠ . 4 6 2 ∴故 错 误 . = 2 +4= 1− 2 +4 ∈ 6 ,3 12.【解析】法1： ，又 ，知 在 上递减，在 1 2 ' 上递增，又当 = 1时 ，= 2 2；=当 2 时， =， ( +1最) 小值 (−∞,−1，)由图可知：(当−1,+ 1 ∞时)， 有唯 一<解0，故 <0 ，且 >0 ， >0 ∴ ( ) ，故=正 确−1；=− >0 从而 = ，设 1 = ， 2 则 1 >0 ∴， 1 令 2 = 2 2 = ， 易知 在 上单调递增，在 ' 1− ' 2 1 2 = ( >0) = = =0 ⟹ = (0, ] 上单调递减， ， ， ，故 正确； 1 1 [ ,+∞) ∴ ≤ = ∴ 1 2 ≤ ∴ ≤ 1 2 ， ，易知 在 上递减，在 上递增， ， ' 1 1 1 1 1 1 = +1=0 ⟹ = ∴ = (0, ) ( ,+∞) ∴ = =− 存在 ，使 ，故 错误； 1 ' ' 1 ∴ =− −1 = =0 令 ，令 ，则 ，易知 在 上递增，又 ' 1 ' ' 1 − = ( − ) = − = − (0,+∞) 2 = ， ， 存在 ，使 ， 在 上递减，在 上递增 ' 1 ' −2<0 1 = −1>0 ∴ 0 ∈(2,1) 0 =0 ∴ (0, 0) ( 0,+∞) （其中 满足 ，即 ）. ， 0 1 0 1 0 = 0 0 =，− 0 ∴ ≥ ， 0 = −， 故 0 正=确 0+ 0 >2 故选 ∴ − = ∙ >2 ∴ − > ∴ ≤2 . . 学科网（北京）股份有限公司法2：对于选项 可以采用如下方法， 由 ， 得 ， ，故 ， 分别为函数 ， 与 的两个交 1 1 1 = 2 2 = = 1 2 = 2 1 2 = = = ( >0) 点的横坐标，由对称性可知点 坐标为 ， ，从而 ， ， ，以 下同解法1. ( 2, 1) ∴ 2 = 2 = 1 1 2 = 1 = 2 ∴ 1 2 = 13. 【详−解6】二项式 的展开式通项公式为 ， ， ， 6 6− ∗ 当r =5时， ( − ) ，所 以 +所1 求=系 6数 为(−. ) ≤6 ∈ 5 6−5 5 5 故答案为： 6 = 6 (− ) =−6 −6 14. 10 −6 【解析】 ， ， 1 1 1 = + −4 ∴ − =sin − +− −4=− − −4  f(x) f(x)8，又 f(3)2，则 f 38210，故答案为：10． 1 15.  3 根据偏导数的定义，在求对x偏导数时， f(x,y)中y可作为常数，即函数可看作是x的一元函数求导，同理 在求对y偏导数时， f(x,y)中x可作为常数，即函数可看作是y的一元函数求导， 所以 f(x,y)2x2y， f(x,y)2x3y2， x y 1 1 1 f(x ,y ) f(x ,y )2x 2y 2x 3y2 3y22y 3(y  )2 ，最小值是 . x 0 0 y 0 0 0 0 0 0 0 0 0 3 3 3 16. 【解析】易知 的方程为 ，从而直线 过定点 ，从而 在直线 上的射影 的轨迹 就是 ： ，当 与 相切时，斜率分别为 ， ，由图可知 =2( −2) (0,2) 2 2 . ⊙ + −3 =1 ⊙ 3 − 3 ∈ −∞,− 3 ∪[ 3,+ ∞) 17． 【详解】解：（1）设等差数列a 的公差为d，则a a d，a a 2d ，…………1分 n 2 1 3 1 学科网（北京）股份有限公司3a 3d 3 a 2 a 4 由题意得 1 ，解得 1 或 1 ，…………………………3分 a 1 a 1 da 1 2d8 d 3 d 3 所以由等差数列通项公式可得a 23(n1)3n5或a 43(n1)3n7． n n 故a 3n5或a 3n7；………………………………5分 n n （2）当a 3n5时，a ,a ,a 分别为1，4，2，不成等比数列；…………6分 n 2 3 1 当a 3n7时，a ,a ,a 分别为1，2，4成等比数列，满足条件． n 2 3 1 3n7, n1,2 故 a  3n7   ，……………………………………………………7分 n  3n7, n3 n(3n11) 记数列a 的前n项和为S ，S  .……………………………………8分 n n n 2 T  a  a  a   a a  a a  S 2S 105.………………10分 20 1 2 20 1 2 3 10 10 2 bc sinBsinC 18．【详解】（1）2asinB  3b，由正弦定理， 3sinBcosB  ，……1分 a sinA 于是 3sinBsinAcosBsinAsinBsinC sinBsin(AB)，…………2分，即 3sinBsinAcosBsinAsinBsinAcosBsinBcosA， 得 3sinBsinAsinBsinBcosA，………………3分 由B(0,π)，则sinB 0，………4分 得到 3sinA1cosA，  π 1 π  π 5π π π 根据辅助角公式可得，sinA   ，结合A 0,π  A    , ，故A  ，可得  6 2 6  6 6  6 6 π A ………………6分 3 1 b2c2a2 （2）法一：在ABC中，由余弦定理得：cosA  ， 2 2bc 得b2 c2 a2 bc，①……………………7分   a 又因为BD DC，所以BDDC  ，且ADBADCπ， 2 即cosADBcosADC0，………………8分 1 △ADB和△ADC中，由余弦定理得b2c2 8 a2，②……………………10分 2 16 联立①②消去a2得b2c2 16bc2bcbc .………………11分 3 学科网（北京）股份有限公司4 3 （当且仅bc 时等号成立）， 3 1 3 4 3 所以ABC的面积S  bcsinA bc . 2 4 3 4 3 所以ABC面积最大值为 .……………………12分 3 法二：延长 至 ，使 ，连 ，则∠ . ° = ，……… … …=…12 8 0分 1 ° 3 △ = △ =2 ∙ ∙sin120 = 4 在 中， ∠ 即 ， ， 2 2 2 2 2 16 当且 △ 仅 当 时 + 成 立−，2 … …∙ … …∙s…in…1 0 分 = + + ≥ 2 + =3 ∴ ≤ 3 = “=” 4 3 ，当且仅当 时， 的面积最大值为 .…………12分 3 3 3 16 4 3 ∴ △ = 4 ≤ 4 × 3 = 3 = △ 19． 【详解】（1）取PC中点M ，连接FM,BM. 1 在PCD中，M,F分别为PC,PD的中点，所以MF //DC,MF  DC. 2 1 在菱形ABCD中，因为AB//DC,BE  DC， 2 所以BE//MF,BEMF. 所以四边形BEMF为平行四边形，所以EF //BM . 又因为EF 平面PBC,BM 平面PBC， 所以EF //平面PBC.（判定定理3条，证明线线平行2分，其余两条1分）……………………4分 （2）因为PD 平面ABCD,DB,DC,DE平面ABCD， 所以PDDB,PDDC,PDDE. 连接BD，因为PB2 PD2BD2,PC2 PD2DC2，且PBPC， 所以BDDC，在菱形ABCD中，AB  BD  AD，即ADB为正三角形. 又因为E为AB中点，所以DEDC，………………………………6分 以D为原点，建立如图所示的空间直角坐标系Dxyz. 学科网（北京）股份有限公司又因为AB∥DC,DE AB. 因为ADB为正三角形且 AD2 3 ，所以DE3. 设F0,0,t(t 0),E3,0,0,C  0,2 3,0  ，……………………7分   则EF 3,0,t,EC   3,2 3,0  ， ur 根据条件，可得平面FCD的法向量为n 1,0,0.……………………8分 1 uur 设平面EFC的法向量为n x,y,z， 2    n EF 0 3xtz0 则 2  ，所以 ， n EC 0 3x2 3y0 2    取x2t，则y 3t,z6，所以n  2t, 3t,6 ，………………10分 2 由题意，二面角EFCD的大小为45，     n n 2t 2 所以 cos＜n,n＞ 1 2   ，解得t 6（舍负）.…………11分 1 2 n n 3t24t236 2 1 2 因为F 是PD的中点，所以PD的长为12.…………12分 经检验符合题意. 1 1 1 3 20. 【解析】（1）得2分即回答1题正确或者回答2题都错误，所以 p2    ，……1分 2 2 2 4 得3分即回答2题1题正确，1题错误或者回答3题都错误， 1 1 1 1 1 5 所以 p3C1      ；………………3分 2 2 2 2 2 2 8 （2）方法1：由题意可知，X 的所有可能取值为n,n1,n2,,nk,,2n.…………4分 n k nk n p(X  nk) Ck    1    1 1  Ck    1   0 k  n,nN* …………5分 n n 2  2 n 2 故X 的分布列如下 n 学科网（北京）股份有限公司X n n1  nk  2n n n n n n 1 1  1 1 P C0  C1   Ck    Cn   n  2 n  2 n  2 n  2 n n n n 1 1 1 1 所以EX   nC0   n1C1  nkCk   2nCn   ……8分 n n  2 n  2 n  2 n  2 n     1 2      n  C n 0 C n 1 C n k C n n C n 1 2C n 2 kC n k nC n n   …………9分 n! n1! 又由kCk  k  n  nCk1………………10分 n k!(nk)! (k 1)!(nk)! n1 C0 C1Ck Cn 2n，C0 C1 Ck Cn1 2n1 …………11分 n n n n n1 n1 n1 n1 n n E(X n )    1 2      n2n n  C n 0 1 C n 1 1 C n n   1 1       1 2      n2n n2n1   3 2 n …………12分 方法2：设回答n次，其中正确回答次数为  ，由于正确回答每题的概率都为 1 ，且每次回答问题是相互独 2 立的，故  B(n, 1 ) ，…………5分 2 又由X 2(n)n …………7分 n 从而X 的分布列及数学期望分别如下 n k nk n 1  1 1   P(X nk) P(k)Ck     1  Ck    0k n,nN* ……10分 n n 2  2 n 2 1 3n …………12分 E(X )E(n)nE()nn  . n 2 2 21. 【解析】（1）易知 ， 1 △ = △ =2∙2∙ ∙ =2 ≤2 =2 =2 5 ，故椭圆的方程为 .…………4分 2 2 ∴（ 2）=法51：设 的方程为 9 + 5 =1， ，由 =2+ 1, 1 , 2, 2 ，…………5分 =2+ 2 2 2 2 ,⟹ 5 +9 +20 −25= 0 9 + 5 =1 ， ， ，…………6分 20 25 1+ 2 4 ∴ 1+ 2 =−5 2 +9 1∙ 2 =−5 2 +9 ∴ 1∙ 2 = 5 学科网（北京）股份有限公司设 ，则 ， ，…………8分 − 1 − 2 ( 9 2, ) 2 = 2 5 1+ 3 = 5 2− 1+ 5 2− 2 2 2 2 25−10 1+ 2 +4 1∙ 2 ∴ = ∙ 1+ 3 5 2 10 − 2 +5 1+ 2 +4 1∙ 2 20 2 25 25−10 ∙ − 2 +4 ∙ − 2 5 +9 5 +9 = ∙ 5 20 25 10 − 2 +5 ∙ − 2 +4 ∙ − 2 5 +9 5 +9 2 2 25 5 +9 +4 = ∙ 2 2 5 10 5 +9 +4 5 1 …………1=2分∙ = . 5 2 2 法2：设 的方程为 ， ，由 =2+ 1, 1 , 2, 2 ，…………5分 =2+ 2 2 2 2 ,⟹ 5 +9 +20 −25= 0 9 + 5 =1 ， ，………………6分 20 25 ∴ 1+ 2 =−5 2 +9 1∙ 2 =−5 2 +9 ，即 ，…………………7分 1+ 2 4 4 ∴ 1∙ 2 = 5 1+ 2 = 5 1∙ 2 设 ，则 9 (2, ) 5 1+ 3 = − 1 + − 2 = 5 − + 2 1+ 2 +2 1∙ 2 5 5 25 5 2 − 1 − 2 − 1+ 2 + 1∙ 2 2 2 4 2 5 − + 5 ∙ 4 1∙ 2+2 1∙ 2 5 − 4 2 1∙ 2 2 5 5 = = 25 5 4 2 25 2 4 −， 2 … 5 … … 1∙… 2 …+… … 1 …∙ 1 2 1分 4 − 1∙ 2 4 = 5 =2∙ 2 .…………12分 2 1 ∴ 1+ 3 =2 22. 【解析】 （1）依题意得， f(0)1a，此时 f(x)sin2 xexx， f(x)sin2xex1，……1分 则切线斜率为 f(0)2，…………2分 故切线方程： y12(x0)，即 y 2x1…………3分 （2）时 ， ，则 ， 2 ' =−1 = − ， − … …4 分 = 2 − −1 ' ∴ = 2 − −1≤− <0 学科网（北京）股份有限公司在 上单调递减，…………5分 ' ∴ 0,2 又 ， ， 值域为 .…………6分 2 2 0 =−1 2 =1− −2 ∴ 1− −2,−1 （3） ， 1 1 = +2 2 − −，2= − − (0< ≤1) ' ； . 减区间为 ，增区间为 ，……7 = −1=0 ⟹ =− ' ' 分 >0 ⟹ >− <0 ⟹ <− −∞,− − ,+∞ . ∴ 当 ≥ 时 ， − =1+ − ， ， 在 上有且仅有一个零点；……8分 当 =1 1时+， 令 − =0 ∴ ( )≥ 0 ∴ ( )，(−∞,+∞) ， 在 上单调递增， ' 1 1− 0< <1 ，… ……=…1+9分 − (0< <1) = −1= >0 ∴ (0,1) ∴又 < ，1 =0 在 上有一个零点，又 ，…………11分 1 0 =0 ∴ (−∞,− ) −2 = +2 − 令 ，则 ， 在 上单调递减， 2 1 ' −1 = − +2， (0< <1) ， =在− <0 ∴ 上 有一(0个,1零) 点.……12分 ∴ 综 上 所述 > ， 1 =0 时， ∴ − 有 2 一 个 > 零 0 点， ∴ (− 时 ， ,−2 有 )2个零点. =1 ( ) 0< <1 ( ) 注：若用无穷远代替x2lna，该2分不给 学科网（北京）股份有限公司学科网（北京）股份有限公司