文档内容
专题 13 立体几何的空间角与空间距离
及其综合应用小题综合
考点 十年考情(2015-2024) 命题趋势
考点1 异面直
2022·全国新Ⅰ卷、2021·全国乙卷、2018·全国
线所成角及其
卷
应用
2017·全国卷、2016·全国卷、2015·浙江卷
(10年6考)
2024·全国新Ⅱ卷、2023·全国乙卷、2022·浙江
考点2 线面角 卷
要熟练掌握几何法和向量法求解
及其应用 2022·全国甲卷、2022·全国新Ⅰ卷、2018·浙江
空间角与空间距离,本节内容是
(10年4考) 卷
新高考卷的常考内容,要熟练掌
2018·全国卷、2018·全国卷、2018·全国卷
握方程思想求值,需强化巩固复
2023·北京卷、2023·全国乙卷、2023·全国新Ⅱ
考点3 二面角 习.
卷
及其应用
2022·浙江卷、2019·浙江卷、2018·浙江卷
(10年6考)
2017·浙江卷、2015·浙江卷
考点4 点面距
及其应用 2019·全国卷
(10年1考)
考点01 异面直线所成角及其应用
1.(2022·全国新Ⅰ卷·高考真题)(多选)已知正方体 ,则( )
A.直线 与 所成的角为 B.直线 与 所成的角为
C.直线 与平面 所成的角为 D.直线 与平面ABCD所成的角为
2.(2021·全国乙卷·高考真题)在正方体 中,P为 的中点,则直线 与 所成的角为( )
A. B. C. D.
3.(2018·全国·高考真题)在正方体 中, 为棱 的中点,则异面直线 与 所成
角的正切值为
A. B. C. D.
4.(2017·全国·高考真题)已知直三棱柱 中, , , ,则异
面直线 与 所成角的余弦值为
A. B. C. D.
5.(2016·全国·高考真题)平面 过正方体ABCD—A B C D 的顶点A, ,
1 1 1 1
, ,则m,n所成角的正弦值为
A. B. C. D.
6.(2015·浙江·高考真题)如图,三棱锥 中, ,点 分
别是 的中点,则异面直线 所成的角的余弦值是 .
考点02 线面角及其应用
1.(2024·全国新Ⅱ卷·高考真题)已知正三棱台 的体积为 , , ,则 与
平面ABC所成角的正切值为( )
A. B.1 C.2 D.3
2.(2023·全国乙卷·高考真题)已知 为等腰直角三角形,AB为斜边, 为等边三角形,若二
面角 为 ,则直线CD与平面ABC所成角的正切值为( )
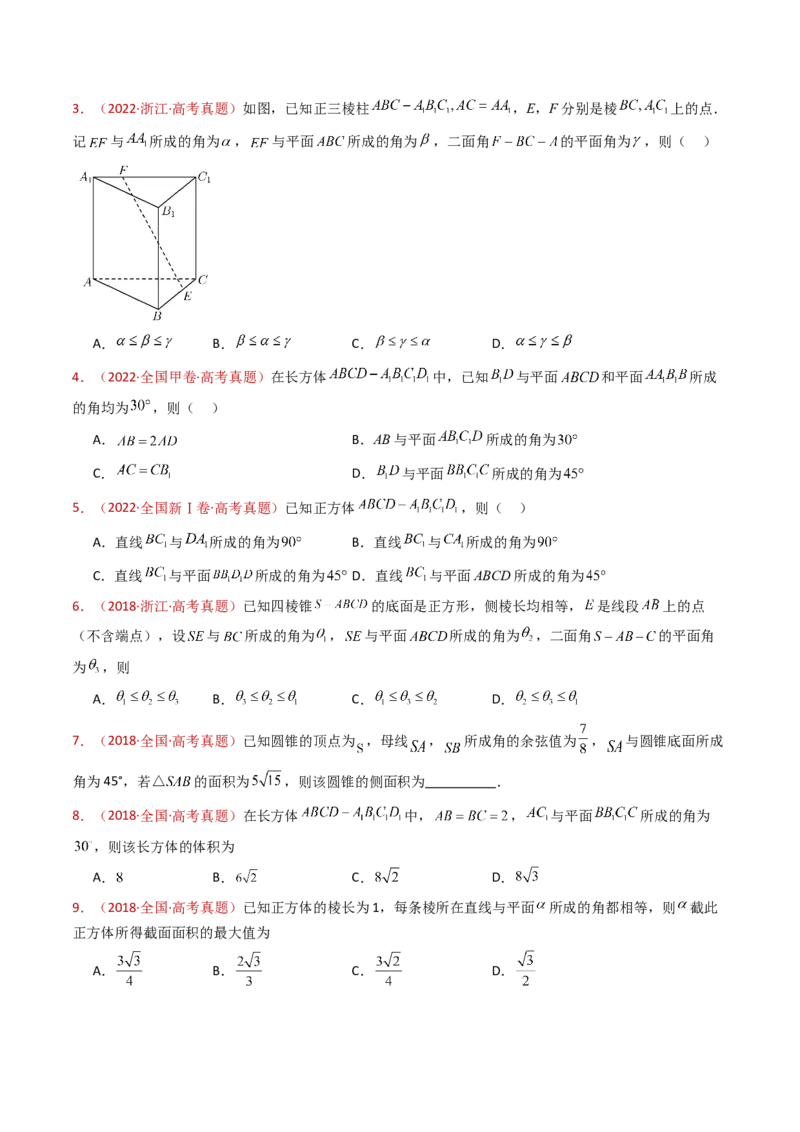
A. B. C. D.3.(2022·浙江·高考真题)如图,已知正三棱柱 ,E,F分别是棱 上的点.
记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A. B. C. D.
4.(2022·全国甲卷·高考真题)在长方体 中,已知 与平面 和平面 所成
的角均为 ,则( )
A. B.AB与平面 所成的角为
C. D. 与平面 所成的角为
5.(2022·全国新Ⅰ卷·高考真题)已知正方体 ,则( )
A.直线 与 所成的角为 B.直线 与 所成的角为
C.直线 与平面 所成的角为 D.直线 与平面ABCD所成的角为
6.(2018·浙江·高考真题)已知四棱锥 的底面是正方形,侧棱长均相等, 是线段 上的点
(不含端点),设 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角
为 ,则
A. B. C. D.
7.(2018·全国·高考真题)已知圆锥的顶点为 ,母线 , 所成角的余弦值为 , 与圆锥底面所成
角为45°,若 的面积为 ,则该圆锥的侧面积为 .
8.(2018·全国·高考真题)在长方体 中, , 与平面 所成的角为
,则该长方体的体积为
A. B. C. D.
9.(2018·全国·高考真题)已知正方体的棱长为1,每条棱所在直线与平面 所成的角都相等,则 截此
正方体所得截面面积的最大值为
A. B. C. D.考点03 二面角及其应用
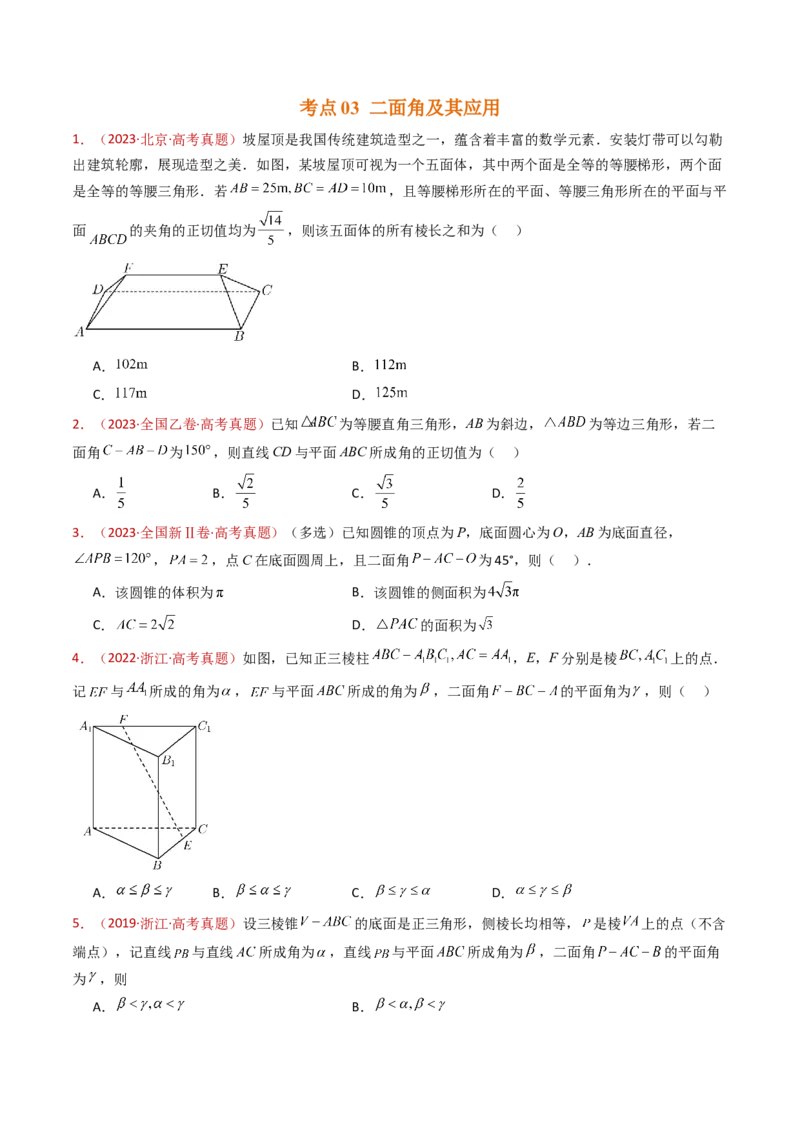
1.(2023·北京·高考真题)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒
出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面
是全等的等腰三角形.若 ,且等腰梯形所在的平面、等腰三角形所在的平面与平
面 的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
A. B.
C. D.
2.(2023·全国乙卷·高考真题)已知 为等腰直角三角形,AB为斜边, 为等边三角形,若二
面角 为 ,则直线CD与平面ABC所成角的正切值为( )
A. B. C. D.
3.(2023·全国新Ⅱ卷·高考真题)(多选)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,
, ,点C在底面圆周上,且二面角 为45°,则( ).
A.该圆锥的体积为 B.该圆锥的侧面积为
C. D. 的面积为
4.(2022·浙江·高考真题)如图,已知正三棱柱 ,E,F分别是棱 上的点.
记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A. B. C. D.
5.(2019·浙江·高考真题)设三棱锥 的底面是正三角形,侧棱长均相等, 是棱 上的点(不含
端点),记直线 与直线 所成角为 ,直线 与平面 所成角为 ,二面角 的平面角
为 ,则
A. B.C. D.
6.(2018·浙江·高考真题)已知四棱锥 的底面是正方形,侧棱长均相等, 是线段 上的点
(不含端点),设 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角
为 ,则
A. B. C. D.
7.(2017·浙江·高考真题)如图,已知正四面体D–ABC(所有棱长均相等的三棱锥),P,Q,R分别
为AB,BC,CA上的点,AP=PB, ,分别记二面角D–PR–Q,D–PQ–R,D–QR–P的平面
角为α,β,γ,则
A.γ<α<β B.α<γ<β C.α<β<γ D.β<γ<α
8.(2015·浙江·高考真题)如图,已知 , 是 的中点,沿直线 将 折成 ,所成
二面角 的平面角为 ,则
A. B. C. D.
考点04 点面距及其应用
1.(2019·全国·高考真题)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的
距离均为 ,那么P到平面ABC的距离为 .