文档内容
高三数学试卷
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷
上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:小题考查集合、常用逻辑用语、不等式、函数、导数、三角函数、数
列、平面向量,大题考查高考范围.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知命题 , ,则p的否定是( )
A. , B. ,
C. , D. ,
2.定义集合 .已知集合 , ,则 的元素的个数
为( )
A.3 B.4 C.5 D.6
3.已知函数 的图象在 处的切线的斜率为 ,则( )
A. 的最小值为6 B. 的最大值为6
C. 的最小值为4 D. 的最大值为4
4.已知某公司第1年的销售额为a万元,假设该公司从第2年开始每年的销售额为上一年的1.2倍,则该公
司从第1年到第11年(含第11年)的销售总额为(参考数据:取 )
A. 万元 B. 万元 C. 万元 D. 万元
5.设函数 的定义域为 ,且 是奇函数, 是偶函数,则( )
学科网(北京)股份有限公司A. B. C. D.
6.设 , ,且 ,则( )
A. B. C. D.
7.已知函数 , ,则“曲线 关于直线 对称”是
“曲线 关于直线 对称”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
8.对称性是数学美的一个重要特征,几何中的轴对称,中心对称都能给人以美感,激发学生对数学的兴趣.
如图,在菱形ABCD中, , ,以菱形ABCD的四条边为直径向外作四个半圆,P是四
个半圆弧上的一动点,若 ,则 的最大值为( )
A. B.3 C.5 D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数 ,则( )
A. 的最小值为1 B. ,
C. D.
10.若正项数列 是等差数列,且 ,则( )
A.当 时, B. 的取值范围是
学科网(北京)股份有限公司C.当 为整数时, 的最大值为29 D.公差d的取值范围是
11.若函数 的定义域为D,对于任意 ,都存在唯一的 ,使得 ,则称
为“A函数”,则下列说法正确的是( )
A.函数 是“A函数”
B.已知函数 , 的定义域相同,若 是“A函数”,则 也是“A函数”
C.已知 , 都是“A函数”,且定义域相同,则 也是“A函数”
D.已知 ,若 , 是“A函数”,则
12.定义在 上的函数 的导函数为 , 且
恒成立,则( )
A.
B. ,函数 有极值
C.
D. ,函数 为单调函数
三、填空题:本题共4小题,每小题5分,共20分.
13.设向量 在向量 上的投影向量为 ,则 ________.
14.若 , ,则 ________.
15.若关于x的不等式 的解集恰有50个整数元素,则a的取值范围是________,这50个
整数元素之和为________.
学科网(北京)股份有限公司16.如图,已知平面五边形ABCDE的周长为12,若四边形ABDE为正方形,且 ,则当 的
面积取得最大值时, ________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分) 的内角A,B,C的对边分别为a,b,c,已知 .
(1)求 ;
(2)若 , 的面积为 ,求 的周长.
18.(12分)如图,在四棱锥 中, 底面ABCD,底面ABCD为正方形, ,E,F,
M分别是PB,CD,PD的中点.
(1)证明: 平面PAD.
(2)求平面AMF与平面EMF的夹角的余弦值.
19.(12分)已知数列 满足 .
(1)求 的通项公式;
(2)求数列 的前n项和 .
20.(12分)某商场在6月20日开展开业酬宾活动.顾客凭购物小票从6~20这15个号码中依次不放回地抽
取2个号码,第1个号码为a,第2个号码为b.设X是不超过 的最大整数,顾客将获得购物金额X倍的商
学科网(北京)股份有限公司场代金券(若 ,则没有代金券),代金券可以在活动结束后使用.
(1)已知某顾客抽到的a是偶数,求该顾客能获得代金券的概率;
(2)求X的数学期望.
21.(12分)以坐标原点为对称中心,坐标轴为对称轴的椭圆过点 , .
(1)求椭圆的方程.
(2)设P是椭圆上一点(异于C,D),直线PC,PD与x轴分别交于M,N两点,证明在x轴上存在两点
A,B,使得 是定值,并求此定值.
22.(12分)已知函数 有两个零点 , .
(1)求a的取值范围;
(2)证明: .
高三数学试卷参考答案
1.A p的否定是 , .
2.B 因为 , ,所以 ,故 的元素的个数为4.
3.C ,当且仅当 时,等号成立,所以 的最小值为4.
4.D 设第 年的销售额为 万元,依题意可得数列 是首项为a,公比为
1.2的等比数列,则该公司从第1年到第11年的销售总额为
万元.
5.C 因为 是奇函数,所以 ,则 .又 是偶函数,所以
,所以 .
6.A 因为 ,所以 ,所以 ,
学科网(北京)股份有限公司即 .又 , ,所以 ,即 或
,即 (舍去).
7.A 令 ,得 ,所以曲线 关于直线
对称.令 ,得 ,所以曲线
关于直线 对称.因为 真包含于
,所以“曲线 关于直线 对称”是“曲线 关于直线
对称”的充分不必要条件.
8.A 如图,设 , ,设P是直线EF上一点,令 ,则 ,
.因为P是四个半圆弧上的一动点,所以当EF与图形下面半圆相切时, 取得最
大值.设线段AB的中点为M,线段AC的中点为 ,连接MP,连接 并延长使之与EF交于点 ,过
M作 ,垂足为N.因为 , ,所以 ,
,则 .
由 ,得 ,故 的最大值为 .
学科网(北京)股份有限公司9.ACD ,A正确.因为当且仅当 时, 取得最小值,且
最小值为1,所以 ,所以 ,B错误.因为 ,所以
,又 ,且 在 上单调递减,在 上单调递增,所以
,C正确.
因为 ,所以 ,所以,D正确.
10.ABC 当 时,公差 , ,A正确.因为 是正项等差数列,所以
,且 ,所以公差d的取值范围是 ,D错误.因为 ,所以 的取值范围
是 ,B正确. ,当 为整数时, 的最大值为29,C正确.
11.BD 对于选项A,当 时, ,此时不存在 ,使得 .A不正确.对于
选项B,由 , 的定义域相同,若 是“A函数”,则对于任意 ,都存在唯一的
,使得 ,则对于任意 ,都存在唯一的 ,使得 ,所
以 也是“A函数”.B正确.对于选项C,不妨取 , , ,令
,则 ,故 不是“A函数”.C不正确.对
于选项D,因为 , ,是“A函数”,所以 在 上恒成立.
学科网(北京)股份有限公司又 ,所以 ,且 ,即对于任意 ,都存在唯一的
,使得 ,因为 ,所以
,由 ,解得 .D正确.
12.AD 设函数 ,
则 ,
所以 在 上单调递减,B错误,D正确.
从而 ,即 ,因为 ,所以 , ,所以
,C错误,A正确.
光速解法:取 ,满足 且 ,则
, ,函数 为单调函数.
13.1 向量 在向量 上的投影向量为 ,则
,解得 .
14. 因为 ,所以 ,所以 ,
学科网(北京)股份有限公司因为 , ,所以 , ,
所以 .
15. ; 或1625 不等式 等价于不等式 .当
时, 的解集为 ,不合题意;
当 时, 的解集为 ,则50个整数解为 , ,…,5,6,所以
,这50个整数元素之和为 ;
当 时, 的解集为 ,则50个整数解为8,9,…,56,57,所以 ,
这50个整数元素之和为 .
综上,a的取值范围是 ,这50个整数元素之和为 或1625.
16. 过点C作 ,垂足为F.设 ,则 ,因为
,所以 ,则 .由 , ,得 .在
中, .记 的面积为S,则
.设函数 ,则
,令 ,得 或 .当
时, ;当 时, .故当 时,
学科网(北京)股份有限公司取得最大值,则S取得最大值,此时 .
17.解:(1)因为 ,所以 . 2分
又 ,所以 . 3分
因为 ,所以 . 4分
又 ,所以 , . 5分
(2) 的面积 ,则 . 7分
由 ,得 , 9分
所以 ,故 的周长为 . 10分
18.(1)证明:取PA的中点N,连接EN,DN,因为E是PB的中点,所以 , .1分
又底面ABCD为正方形,F是CD的中点,所以 , ,所以四边形ENDF为平行四边形,
所以 . 3分
因为 平面PAD, 平面PAD,所以 平面PAD. 4分
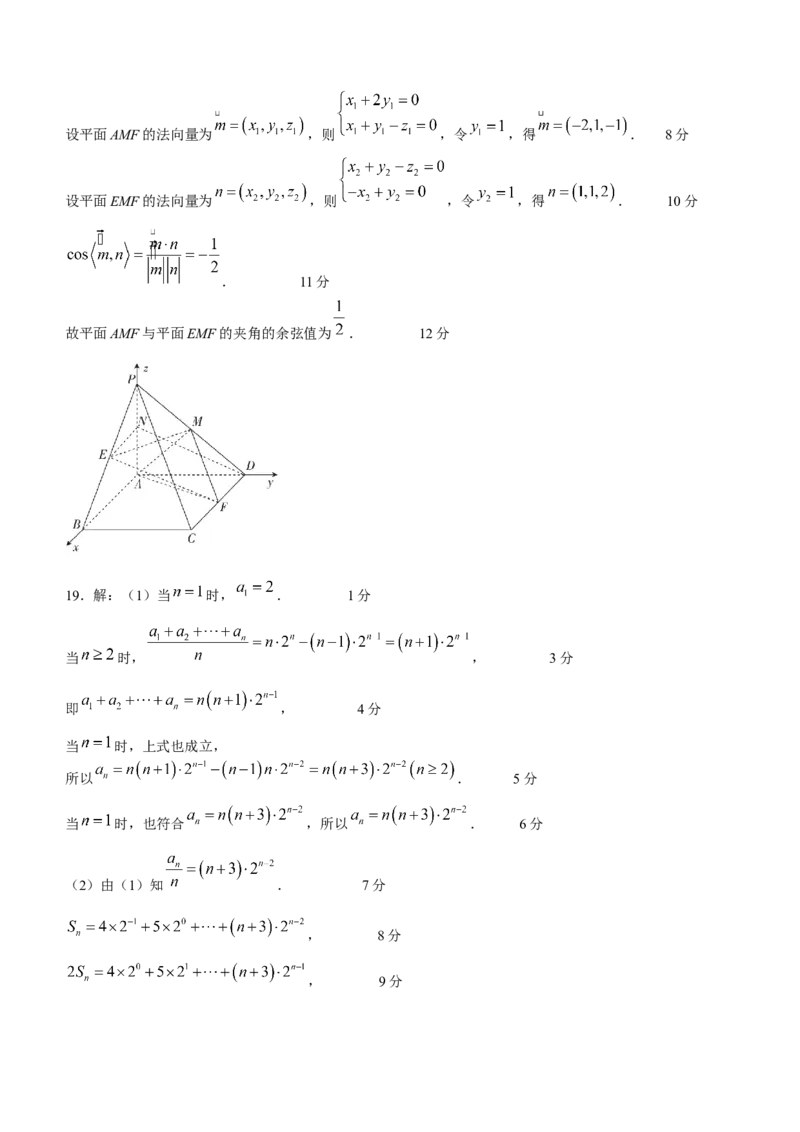
(2)解:以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
令 ,则 , , , , . 5分
从而 , , . 6分
学科网(北京)股份有限公司设平面AMF的法向量为 ,则 ,令 ,得 . 8分
设平面EMF的法向量为 ,则 ,令 ,得 . 10分
. 11分
故平面AMF与平面EMF的夹角的余弦值为 . 12分
19.解:(1)当 时, . 1分
当 时, , 3分
即 , 4分
当 时,上式也成立,
所以 . 5分
当 时,也符合 ,所以 . 6分
(2)由(1)知 . 7分
, 8分
, 9分
学科网(北京)股份有限公司则 , 11
分
所以 . 12分
20.解:(1)当 时,该顾客能获得代金券.设“a是偶数”为事件A,,“ ”为事件B,则
, 2分
, 3分
所以 ,所以当顾客抽到的a是偶数时,该顾客能获得代金券的概率为 . 4分
(2)X可能的取值为0,1,2,3.
当 时, ,则 . 5分
当 时, ,若 ,则 .对每一个a,b有 种不同的取值,则
共有 种可能的取值. 6分
若 ,对每一个a,b有 种不同的取值,则 共有 种可能的取值,所以
. 7分
当 时, .
若 ,则 .对每一个a,b有 种不同的取值,则 共有 种情况.
若 ,则 , 共有6种可能的取值.所以 . 9分
当 时, , 只有 , , 这3种情况,所以
. 10分
学科网(北京)股份有限公司所以 . 12分
21.(1)解:设椭圆方程为 , 1分
则 ,解得 , 3分
所以椭圆的方程为 . 4分
注:若直接设 得到 ,扣1分.
(2)证明:设 , , ,
直线 ,令 ,得 . 5分
直线 .令 ,得 . 6分
. 8分
令 ,
令 , ,得 , , 10分
则 .
故存在 和 ,使得 是定值,且定值为 . 12分
22.(1)解:令 ,得 ,则 . 2分
学科网(北京)股份有限公司令函数 ,则 ,
因为 在 上单调递增,所以 ,即 . 3分
令函数 ,则 ,则 在 上单调递减,在 上单调递增,所以
. 4分
因为当 时, ,当 时, , 5分
依题意可得方程 有两个不相等的正根,所以 ,即a的取值范围是 . 6分
(2)证明:令函数 ,则 ,
所以 在 上单调递减. 7分
因为 ,所以当 时, ;当 时, . 8分
不妨假设 ,则由(1)知 ,所以 , ,
所以 ,则 , 9分
,则 , 10分
所以 , 11分
因为 ,所以 . 12分
学科网(北京)股份有限公司