文档内容
2024届新高三开学摸底考试卷(九省新高考专用)02
数学·答案及评分标准
1 2 3 4 5 6 7 8 9 10 11 12
D B A C A B B D CD AC ABD ABD
13.5 14.20
15.12 16.③④
17.【详解】(1)由题意可知 , ,
所以 ,(2分)
又因为 ,
所以 ,解得 ,
所以 .(4分)
(2)由(1)可知 , ,所以 , ,(5分)
所以由三角函数的定义可得 , ,
, ,(8分)
所以 .(10分)
18. 【详解】(1)根据题意,设该等比数列的公比为q,
若 ,(2分)
则有 或 或 .(4分)
又由数列{a}是递增的等比数列,则 ,则有 ,
则数列{a}的通项公式 ;(6分)(2)由(1)可得 ,则 ,
则 ,(8分)
则
.(12分)
19.【详解】(1)取 的中点 ,则 ,(1分)
又 平面 平面 ,平面 平面 平面 ,
平面 , 平面 ,
,(3分)
, 平面 ,
平面 , 平面 ,
,(5分)
又 .(6分)
(2)在平面 内过 作 的垂线
以 为坐标原点, 正方向为 轴,可建立如图所示空间直角坐标系,
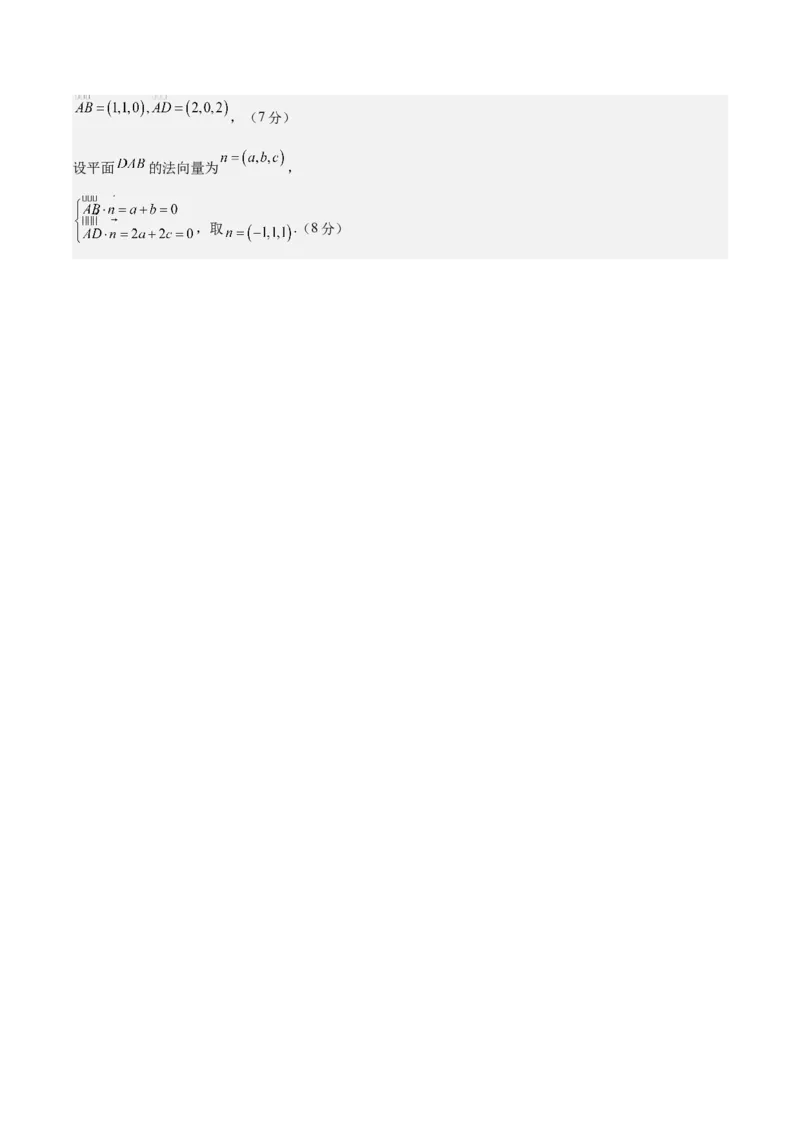
则 ,,(7分)
设平面 的法向量为 ,
,取 .(8分)设 ,
设平面 的法向量为 ,
,(10分)
平面 与平面 夹角的余弦值是 ,
,
,
或 (舍),
.(12分)
20.【详解】(1)因为点 为线段 的垂直平分线与半径 的交点,
所以 ,所以 ,(2分)
所以点 的轨迹是以 为焦点,长轴长为4的椭圆,在椭圆中 ,
所以曲线 的方程为 .(4分)
(2)由已知得 ,所以直线 的方程为 ,所以 点的坐标为 .(5分)
当直线 的斜率不存在时, ,
或 都与已知不符;(6分)
当直线 的斜率存在时,设直线 的方程为 ,由 得 ,
易知 ,则 ,(8分)
,
由 的面积是 面积的 倍可得 ,化简得 ,即 ,(10分)
又 ,所以 ,即 ,也就是 ,
所以 ,
解得 ,
所以直线 的方程为 .(12分)
21.【详解】(1)解:由函数 ,可得 定义域为 ,(1分)
且 ,(2分)
令 ,可得 ,所以 单调递增,(3分)
又因为 ,(4分)
所以当 时, ,可得 , 单调递减;
当 时, ,可得 , 单调递增,
所以当 时,函数 取得极小值,极小值为 ,无极大值. (5分)
(2)解:由 ,因为 且 ,可得 ,(6分)
令 ,
可得 ,
因为 ,即 或 ,又因为方程 的两根都是负数根(舍去),
所以 ,可得 ;(8分)
当 时, , 单调递减;
当 时, , 单调递增,
所以当 时,函数 取得极小值,同时也为 在 上的最小值,(10分)
即 ,所以 ,
所以 ,所以 ,
故当 时, 在 恒成立. (12分)
22.【详解】(1)设等差数列 的公差为 ,
由题意可得: ,解得 或 (舍去),
所以 .(4分)
(2)由(1)可得 ,(5分)
当 为奇数时,则 ,
设 ,
则 ,(6分)
两式相减得
,所以 ;当 为偶数时,则 ,
设 ,
所以 ;(8分)综上所述: ,(10分)
当 为奇数时,则
;
当 为偶数时,则
;
综上所述: .(12分)公众号:高中试卷君