四川省广安市高2023级第一次模拟考试数学答案(1)_2026年1月_260118四川省广安市高2023级第一次模拟考试（广安一诊）（全科）

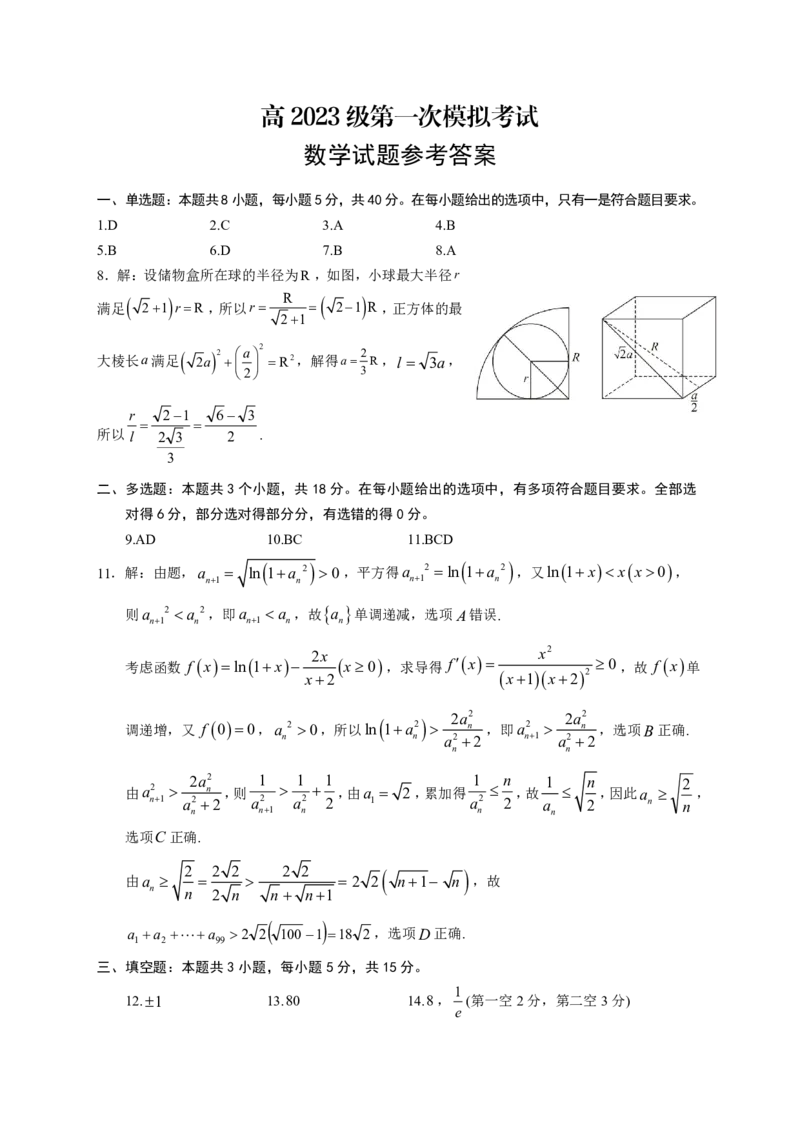
高 2023 级第一次模拟考试 数学试题参考答案 一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一是符合题目要求。 1.D 2.C 3.A 4.B 5.B 6.D 7.B 8.A 8．解：设储物盒所在球的半径为R，如图，小球最大半径r   R   满足 21 rR ，所以r   21 R ，正方体的最 21 2  2 a 2 大棱长a满足 2a   R2，解得a R，l  3a， 2 3 r 21 6 3   所以 l 2 3 2 . 3 二、多选题：本题共3个小题，共18分。在每小题给出的选项中，有多项符合题目要求。全部选 对得6分，部分选对得部分分，有选错的得0分。 9.AD 10.BC 11.BCD 11．解：由题，a  ln  1a 2  0，平方得a 2 ln  1a 2  ，又ln  1x  x  x0  ， n1 n n1 n 则a 2 a 2，即a a ，故  a  单调递减，选项A错误. n1 n n1 n n 考虑函数 f  x ln  1x  2x  x0 ，求导得 f x  x2  0，故 f  x  单 x2  x1  x2 2 调递增，又 f  0 0，a 2 0，所以ln  1a2   2a n 2 ，即a2  2a n 2 ，选项B正确. n n a2 2 n1 a2 2 n n 2a2 1 1 1 1 n 1 n 2 由a2  n ，则   ，由a  2，累加得  ，故  ，因此a  ， n1 a2 2 a2 a2 2 1 a2 2 a 2 n n n n1 n n n 选项C正确. 2 2 2 2 2   由a     2 2 n1 n ，故 n n 2 n n  n1   a a a 2 2 100 1 18 2，选项D正确. 1 2 99 三、填空题：本题共3小题，每小题5分，共15分。 1 12.1 13.80 14.8， (第一空2分，第二空3分) e14. 解：由 OP 2， x  y 2，所以面积S=8, 设 ，则 MN  x x  ex 1ex 2 ， 1 2 1 2 1, 1−1 , 2, 则 MN 在x  x 或ex 1ex 2 时，取得最小值， 1 2 1 若x x ，则令 ，则 ，令 ，解得 ， 1 2 ( )= − +1 '( )= − '( )= 0 =1 当 时， ，函数 单调递减， 当 ∈ −∞,1 时， '( )<0 ，函数 ( )单调递增， ∈ 1,+∞ '( )>0 ( ) 则 时， ，即 MN 1； min = 1 ( )min = −e+1 =1 若 ，即有 ，则令 ， 2 1−1= 2 = ( 1−1) ℎ( )= − ( −1) 则 ，令 ，解得 ， 1 ℎ'( )= 1− −1 ℎ'( )= 0 = 1+ 当 时， ，函数hx单调递减， 1 ∈ −∞,1+ ℎ'( )< 0 当 时， ，函数hx单调递增， 1 ∈ 1+ ,+∞ ℎ'( )>0 则 时， ； 1 1 1 = 1+ ℎ( ) = ℎ 1+ = 1 综上所述， MN  . min e 四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。 15．解：（1）设等差数列{a }的公差为d，因为2a a n2， n n1 n 2a a 3 则 2 1 ， ……2分 2a a 4 3 2 a +2d 3 a 1 即 1 ，解得 1 ， ……4分 a 3d 4 d 1 1 所以a a n1d n. 则数列a 的通项公式为a n . ……6分 n 1 n n （2）因为数列{a b }是首项为1，公比为2的等比数列，则a b 2n1， ……8分 n n n n 又因为a n，所以b 2n1n. ……9分 n n 设数列b 的前n项和为S ， n n 则S   1242n1 123n ……10分 n 12n nn1 n2n   2n1 12 2 2所以数列b 的前n项和为2n1 n2n . ……13分 n 2 16．解：（1）如图，设BC3，取AD的中点H，连接BH ． ……1分 因为AD2BC，所以BCDH ． 又AD//BC，BCCD，BC CD，所以四边形BCDH为正方形， 所以ABBD3 2，AD6． ……3分 因为AB2BD2 AD2，所以 ． ……4 分 ⊥ 又平面ABEF 平面ABCD，平面ABEF 平面ABCD AB，BD平面ABCD， 所以 平面ABEF． ∩ ……5 分 ⊥ 因为BD平面BDG，所以平面BDG平面ABEF． ……6分 （2）因为平面ABEF 平面ABCD，平面ABEF平面ABCD AB， BE  AB，BE平面ABEF，所以BE 平面ABCD， BH,BC 平面ABCD，所以BE BH ，BE BC，由（1）BH BC， 所以BH ，BC，BE两两垂直，    以B为原点， BH ，BC， BE 的方向分别为x,y,z 轴的正方向， 建立如图所示的空间直角坐标系．设BC3， ……8分 则A3,3,0，B0,0,0，D3,3,0，G(0,1,2 2)，  所以BD3,3,0，BG (0,1,2 2)． ……9分  设平面BDG的法向量为nx,y,z，   nBD 3x3y 0 2 则 取x1，得n(1,1, )． ……11分  nBG  y2 2z 0 4 因为BDAB，BE  AB，BEBDB ，BE,BD平面BED，  所以AB平面BDE，所以平面BDE的一个法向量为BA3,3,0， ……13分 BAn 4 17 设平面EBD与平面GBD的夹角为，则cos  BA n 17 4 17 即平面EBD与平面GBD夹角的余弦值为 ． ……15分 17 17．解：（1） ， ……2分∵ cos + 3 sin =1+2 = +2 在△ABC中，由正弦定理得sinBcosC 3sinCsinB sinA2sinC ， ……3分由三角形内角和为180可得sinAsinBC， sinBcosC 3sinCsinB sin BC 2sinCsinBcosCcosBsinC2sinC， 即 3sinCsinBcosBsinC 2sinC ， 3 1 ，sinC0， 3sinBcosB2, sinB cosB1 ， ∘ ∘ 2 2 ∵0 < <180   即sin B30 1， ……5分 又 0 B180，B3090，即B120. ……7分 （2）设AC AD，令DCACDA，CAD1802， AC CD 在ACD中，由正弦定理得，  ，CD 3， sinD sinCAD 3sin 3 AC   . ……9分 sin2 2cos AC BC 在ABC中，由正弦定理得，  ，BAC 60，BC1， sinB sinBAC sin120 AC    ， ……11分 sin 60     sin 60 cossin 90 ，解得 . …… ∘ α=75 13分 ， ∴∠ C D=180°−2 =30° 2R  2 3,R  3. ……15分 sinCAD 1 18．解：（1）由题，甲在第三局获胜，此时甲必须连胜3局，故p  ； ……2分 3 27 甲在第五局获胜，此时，乙在前三局中获胜一局， 4 2 1 2 其余局数都是甲获胜，故 p C1    . ……5分 5 3 3 3 81 （2）由题，X 的取值为3，2，1,0,1,2,3，故q 1，q 0，记事件A 为X k时，甲最终获得 3 3 k 训练赛胜利，则q PA ，考虑下一局比赛，事件B为甲获胜，由全概率公式得， k k PA PA |BPBP  A |B  P  B  ，即PA PA PBPA P  B  ， k k k k k1 k1 1 2 因此q  q  q . ……8分 k 3 k1 3 k1 整理得q q 2q q ，因此q q 是公比为2的等比数列. ……11分 k1 k k k1 k1 k （3）由题，甲获得训练赛胜利的概率为q . 0记a q q ，则q q a a a a a a 1， ……13分 k k1 k 3 3 2 1 0 1 2 3 由公比为2，则a  1222232425 1，故a  1 . ……15分 3 3 63 1 2 4 1 因为a a a a 2a 4a     ， 3 2 1 3 3 3 63 63 63 9 1 又a a a q q q q q q q q q ，所以q  . 3 2 1 2 3 1 2 0 1 0 3 0 0 9 1 即甲获得训练赛胜利的概率为 . ……17分 9 19．解：（1）由g x 1lnx， ……1分 当0 xe时，g(x)0，则g  x  单调递增； ……2分 当xe时，g(x)0,则g  x  单调递减. ……3分 故g  x  的增区间为  0，e  ，减区间为  e， ； ……4分 （2）①设直线l与曲线 y  f x和曲线 y  f x分别切于点Px ,k，Qx ,k， a1 a2 1 2 由 f  x ex a ，则ex 1 a 0，ex 1 a x a k，消去a 得，  2x  ex 1 k， a 1 1 1 1 1 1 1 1 同理  2x  ex 2 k；故方程  2x  ex k 有两个不同的解. ……6分 2 设h(x) 2x  ex，h(x) 1x  ex，当x1时，h(x)0，则h(x)单调递增；当x1时， h(x)0,则h(x)单调递减. ……7分 当k 0,e  时，h(1)ek ，h(2)0k ，因此x  1,2  使得h  x k ； 2 2 由ex  1 1 x  x1 ，所以 e k k  1 2 k 1 ，则h( k k  1 2 )k ，因此x 1     k k  1 2 ,1   使得h  x 1 k . 当k，0  时，由x1，h(x)0，又h(x)在  1， 上单调递减， 故方程  2x  ex k 至多一个解. 当k e, 时，由h(x)（h 1）e，故方程  2x  ex k 至多一个解.   综上，k的取值范围为 0,e .（说明：用极限证明扣1分） ……9分 ②选择（ⅰ） 由①知  2x  ex 1 k，  2x  ex 2 k，x 1，1 x 2， 1 2 1 2故  2lnex 1  ex 1   2lnex 2  ex 2 k ，即g  ex 1   g  ex 2  k . ……11分 考虑函数m  x  g(x)x  x  1lnx  ,x 0,e  ，故m  x 0， 由ex 1  0,e  ，得m  ex 1   g(ex 1)ex 1 k ex 1 0，即k ex 1 . ……13分 考虑函数n  x  g(x)xe2  x  3lnx e2，x  e,e2  ，n x 2lnx 0， 故n  x  在  e,e2  上单调递增. ……15分 由n  e2  0，故n  x 0.由ex 2   e,e2  ，得n  ex 2   g(ex 2)ex 2 e2 k ex 2 e2 0 ， 即e2 k ex 2. 综上ex 1 ex 2 e2，即a a e2 ……17分 1 2 ②选择（ⅱ），由①知  2x  ex 1 k，  2x  ex 2 k，x 1，1 x 2， 1 2 1 2 故k2 ex 1 x 2  2x  2x aa  2x  2x  . ……11分 1 2 1 2 1 2 下面证明  2x  2x 1， 1 2 设m2x 1，n2x ，0n1，mem nen ke2， ……13分 1 2 故lnmmlnnnlnk2. ……14分 设t(x)lnxx，T(x)t  x t   1 ，T(x)t x  1 t   1     x1  2 ，  x x2 x  x  1 当x 0,1  时，T(x)0，T(x)单调递减，因此T  n T  1 0，即t  n t ， n 1 1x 由t  m t  n  ，则t  m t .又t(x) ， ……16分 n x 1 当x 1, 时，t(x)0，t(x)单调递减，故m ， n 因此aa k2. ……17分 1 2