文档内容
2024年高考押题预测卷02【北京卷】
数学·参考答案
第一部分(选择题 共40分)
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1 2 3 4 5 6 7 8 9 10
A D C D B A B B D C
第二部分(非选择题 共110分)
二、填空题:本题共5小题,每小题5分,共25分。
11. 12. 4 13. 1 14.4 3或4 15.②③
三、解答题:本题共6小题,共85分。解答应写出文字说明、证明过程或演算步棸。
16.(14分)
【分析】(1)由等腰三角形和直棱柱的性质,得出 和 ,根据线面垂直的判定定理,即
可证出 平面 ;
(2)连接 ,交 于点 ,连接 ,结合三角形的中位线得出 ,根据线面平行的判定定理,
即可证出 平面 ;
(3)连 ,交 于点 ,分别取 、 中点 、 ,连接 、 、 ,根据线面垂直的判定
定理,可证出 平面 和 平面 ,从而得出 就是二面角 的平面角,
最后利用几何法求出二面角 的余弦值.
【详解】解:(1)证明: , 是 中点, ,
又 在直三棱柱 中, 平面 , 平面 ,
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司,
又 , 平面 , 平面 ,
平面 .
(2)证明:连接 ,交 于点 ,连接 ,
、 分别是 、 的中点,
是 的中位线, ,
平面 , 平面 ,
平面
(3)解:连 ,交 于点 ,分别取 、 中点 、 ,连接 、 、 ,
四边形 是正方形且 、 分别是 、 的中点,故 ,
在 中, , ,
, ,
又 , 分别是 , 中点且 ,
,
又 在直三棱柱 中, 平面ABC, 平面ABC,
,
, 平面 , 平面 ,
平面 ,
平面 , 平面 ,
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司, ,
又 , , 平面 , 平面 ,
平面 ,
平面 , ,
又 平面 平面
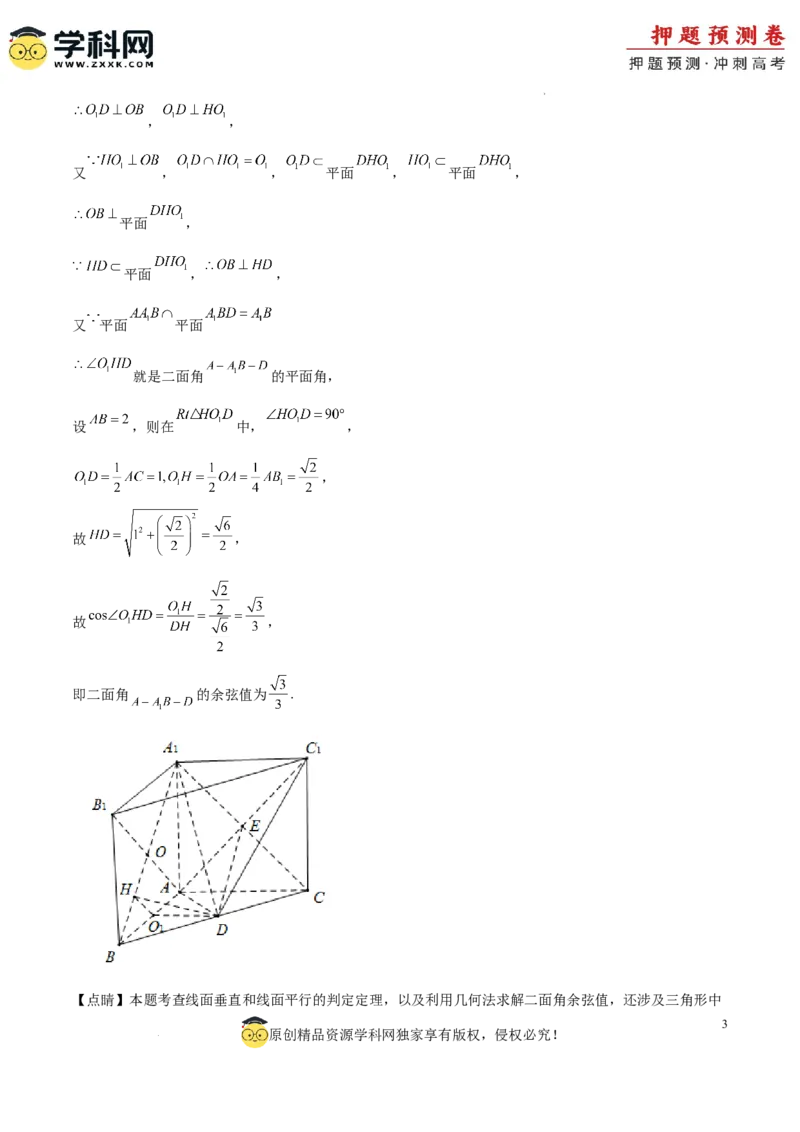
就是二面角 的平面角,
设 ,则在 中, ,
,
故 ,
故 ,
即二面角 的余弦值为 .
【点睛】本题考查线面垂直和线面平行的判定定理,以及利用几何法求解二面角余弦值,还涉及三角形中
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司位线和勾股定理的逆定理的运用,考查推理证明能力和运算能力.
17.(13分)
【分析】(1)利用正弦定理边化角,结合同角公式计算即得.
(2)选择条件①,利用余弦定理及三角形面积公式计算求解;选择条件②,利用正弦定理计算判断三角
形不唯一;选择条件③,利用正弦定理计算判断,再求出三角形面积.
【详解】(1)由 得: ,而 ,
则 , 为锐角,又 ,解得 ,
所以 且 为锐角.
(2)若选条件①,由 , 为锐角,得 ,
由余弦定理得 ,又 ,则 ,
解得 唯一确定,所以 .
若选条件②,由正弦定理得 ,则 ,
由 ,得 ,因此角 有两解,分别对应两个三角形,不符合题意.
若选条件③,由 , 为锐角,得 ,
又 ,得 , ,则 ,
因此 唯一确定,
由正弦定理得 ,则 ,所以 .
18.(13分)
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【分析】(1)由题意得, ,从而求解 ,再结合表格数据与学生总人数求解 ;(2)先求解样
本符合题意的概率,然后由样本估计总体,得全市学生符合题意的概率,从而利用对立事件的概率公式求
解;(3)表示出参赛学生理论竞赛的平均成绩与方差,从而得关于 二次函数,由 的取值范围与二次函
数的性质从而求解得答案.
【详解】(1)由题意,理论或操作至少一项成绩为300分的学生
共有 人,则 ,
得 ,又 ,
得
(2)由(1)知,从20位理论成绩为300分的学生中抽取1人,
操作成绩也为300分的概率为 ,所以从全市理论成绩为300分的学生中,
随机抽取2人,至少有一个人操作的成绩为300分的概率为
(3)由题意, ,
设理论竞赛的分数为 ,则 取值为 ,
对应的人数分别为 ,所以参赛学生理论竞赛的平均成绩为
,
所以参赛学生理论成绩的方差为
因为 ,所以当 时, 最小.
【点睛】求解本题的关键是将理论竞赛分数对应的人数表示为 的多项式,然后求解均值与方差,从而转
化为关于 的二次函数的最值问题.
19.(15分)
【分析】(1)根据椭圆的顶点坐标,结合斜率的计算公式,可整理椭圆方程,建立方程,可得答案;
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)由题意,利用三角形中线性质,分割三角形,整理三角形面积表达式,联立直线与椭圆方程,写出
韦达定理,求得面积表达式中的变量,利用基本不等式,可得答案.
【详解】(1)由已知得 , 且 ,即 ,
因此有 ,得 .
因此 ,得 , ,所以椭圆的标准方程为 .
(2)显然直线 经过x轴上的定点 ,设 , ,
则由椭圆的对称性得 ,
联立 ,消去x得 .
恒成立,所以 , .
.
令 ,显然有 ,于是 ,当 ,即
时取等号.
因此 的面积S的最大值为 .
20.(15分)
【分析】(1)对 , 进行求导,已知在交点处有相同的切线,从而解出 的值及该切线的方程;
(2)由条件知 ,对 进行求导,分两种情况进行讨论:① ;② ,从而
求其最小值 的解析式;
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】(1)解: ,
由已知得 ,解得 ,
两条直线交点的坐标为 ,切线的斜率为 ,
切线的方程为 ,即切线的方程为 .
(2)解:由条件知
①当 时,令 ,解得 ,
当 时, 在 上递减;当 时, 在 上递增,
是 在 上的唯一极值点,从而也是 的最小值点,
最小值点, .
②当 时, 在 上递增,无最小值,故 的最小值 的解析式为
.
【点睛】本题主要考查导数的几何意义、利用导数研究函数的单调性从而求最值、分类讨论思想.属于难题.
分类讨论思想解决高中数学问题的一种重要思想方法,是中学数学四种重要的数学思想之一,尤其在解决
含参数问题发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透,这样
才能快速找准突破点. 充分利用分类讨论思想方法能够使问题条理清晰,进而顺利解答,希望同学们能够
熟练掌握并应用与解题当中.
21.(15分)
【分析】(1)直接利用信息求出数列的项.
(2)利用恒成立问题和函数的单调性,求出λ的取值范围.
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(3)直接利用分类讨论思想求出数列的通项公式.
【详解】(1)数列 为“Γ数列”中, ,
所以:当 时, 时, ,
又 ,即: ,
, .
(2)因为数列 是“Γ数列”,且 ,所以:
,
则:数列前4n项中的项bn 是以2为首项,6为公差的等差数列.
4 -3
易知{bn}的项后按原来的顺序构成一个首项为4,公差为2的等差数列.
4
所以:
,
.
由于不等式 对 恒成立,
所以: ,
设 ,
则: ,
所以:
当 时, ,
当 时, ,
所以:
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 的最大值为 .
即 .
(3) 为等比数列,设数列 的公比 ,
由等比数列的通项公式: ,
当 时, ,
即: ,
① ,则 ,故: .
②当 时,则: ,
所以 为常数,则 ,k为偶数时,
经检验,满足条件数列 的通项公式为: 或 .
【点睛】本题考查的知识要点是数列的通项公式的求法及应用,函数的单调性的应用,主要考查学生的运
算能力和转化能力,属于中档题.
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司