文档内容
2024届新高三开学摸底考试卷(全国通用)
理科数学·答案及评分标准
1 2 3 4 5 6 7 8 9 10 11 12
A B D C B B C B A D B C
13. 14.164
15. 16.1
17.【解析】(1)证明:取AB的中点 ,连接 ,则由题意知 为正三角形,
所以 ,
由等腰梯形知 ,设 ,则 , ,
故 ,即得 ,所以 ,(2分)
因为平面 平面 , ,平面 平面 , 平面PAD,
所以 平面 ,又 平面 ,所以 ,(4分)
因为 , , 平面 ,所以 平面 ,
因为 平面 ,所以 .(6分)
(2)由(1)得 , , 两两垂直,以 为坐标原点, , , 所在直线分别为 , , 轴建立空间直
角坐标系,
因为 平面 ,所以 平面 所成的角为 ,
设 ,则 , ,
则 , , , ,
则 , , ,(8分)
设平面PAB的法向量为 ,则 ,即 ,
取 ,则 ,(9分)
设平面PBC的法向量为 ,
则 ,即 ,
取 ,则 ,(10分)
所以 ,
所以二面角 的正弦值为 .(12分)
18.【解析】(1) ,
当 时, ,即 ,
得 或 (舍去). (1分)
由 ,……①
得 ,……②
得: ,
化简得 .(3分)
因为 ,所以 , ,
即数列 是以4为首项,2为公差的等差数列, (5分)
所以 .(6分)(2)存在. (7分)
当 , 时,
会得到数列 中原次序的一列等比数列 ,
此时的公比 ,是最小的,此时该等比数列的项均为偶数,均在数列 中;(8分)下面证明此时的公比最小:
,假若 取 ,公比为 ,
则 为奇数,不可能在数列 中. (10分)
所以 .
又 ,所以 ,即 的通项公式为 ,
故 .(12分)
19.【解析】(1)(i)依题意得 列联表如下:
正确识别 错误识别 合计
组软件 40 20 60
组软件 20 20 40
合计 60 40 100
(2分)
因为 ,(3分)
且 ,
所以没有 的把握认为软件类型和是否正确识别有关;(5分)
(ii)由(i)得 ,(6分)
故方案二在一次测试中通过的概率为
;(8分)
(2)方案二每次测试通过的概率为
,所以当 时, 取到到最大值 ,(10分)又 ,此时 ,
因为每次测试都是独立事件,
故 次实验测试通过的次数 ,期望值 ,
因为 ,所以
所以测试至少27次,此时 .(12分)
20.【解析】(1)由题可得 ,故可得 ,(2分)
则 ,(3分)
故 的标准方程为 .(4分)
(2)由(1)中所求可得点A, 的坐标分别为 ,
又双曲线渐近线为 ,显然直线 的斜率不为零,
故设其方程为 , ,(5分)
联立双曲线方程 可得: ,
设点 的坐标分别为 ,
则 ,
,
;(6分)
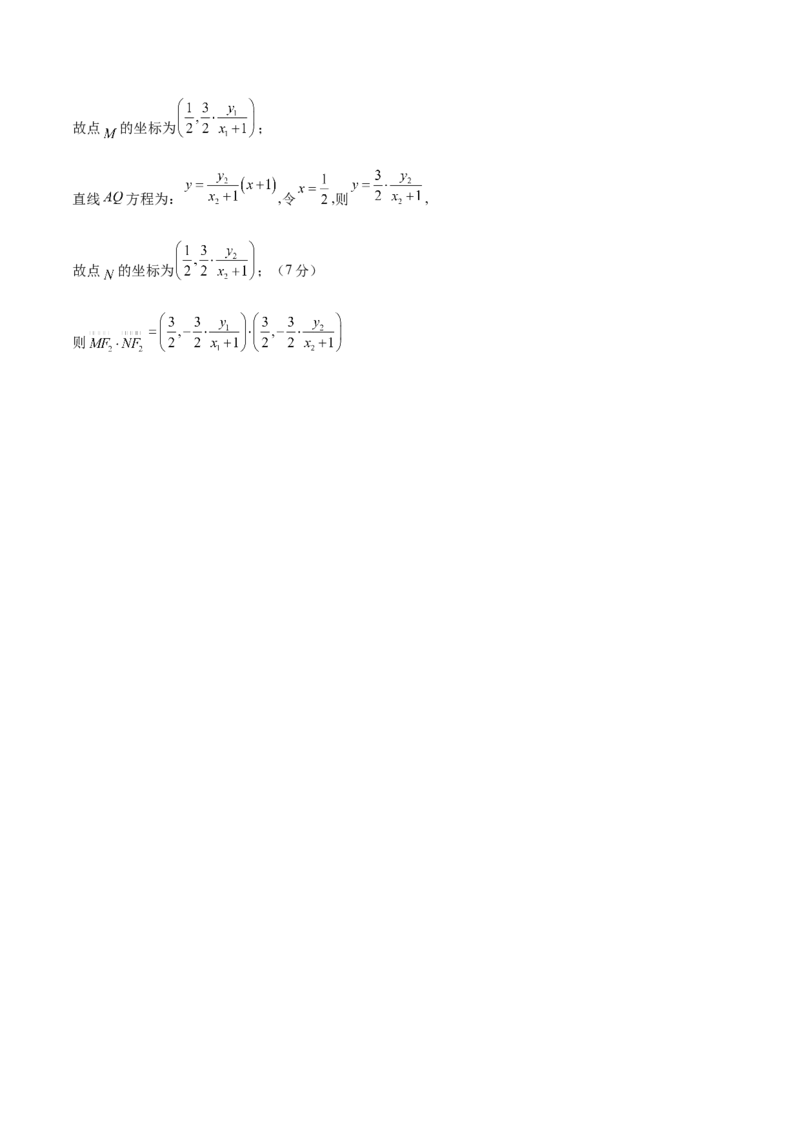
又直线 方程为: ,令 ,则 ,故点 的坐标为 ;
直线 方程为: ,令 ,则 ,
故点 的坐标为 ;(7分)
则故 为定值 .(8分)
(3)当直线 斜率不存在时,
对曲线 ,令 ,解得 ,
故点 的坐标为 ,此时 ,
在三角形 中, ,故可得 ,
则存在常数 ,使得 成立;(9分)
当直线 斜率存在时,
不妨设点 的坐标为 , ,直线 的倾斜角为 ,直线 的倾斜角为 ,
则 , ,
假设存在常数 ,使得 成立,即 ,
则一定有 ,也即 ;
又 ; ;
又点 的坐标满足 ,则 ,故
;(11分)
故假设成立,存在实数常数 ,使得 成立;
综上所述,存在常数 ,使得 恒成立. (12分)
21.【解析】(1)函数 的定义域为 .(1分)①若 时,
1
- 0 + 0 -
极小值 极大值
(2分)
②若 时, 恒成立, 单调递减,
③若 时
1
- 0 + 0 -
极小值 极大值
(3分)
④若 时, 时, 单调递减; 时, 单调递增.
综上所述,当 时, 单调递减, 单调递增, 单调递减;当 时,
单调递减;当 时, 单调递减, , 单调递增,
单调递减;当 时, 单调递减, 单调递增. (4分)
(2)(i)由(1)知当 时, 单调递减,
单调递增,
单调递减.
所以 存在三个零点,只需 和 即可,
所以 且 ,整理得 且 .
此时, , (6分)
令 ,易知 在 上单调递减
有 ,
所以 .(8分)
(ii)由(1)知,当 时, 单调递减,
单调递增,
单调递减
所以 .若 存在三个零点,只需 和 即可,
所以 且 ,
整理得 ,
因为 ,
设 ,则方程 ,即为
记 ,
则 为方程 三个不同的根, (10分)
设 .
要证: ,即证: ,
即证: ,
而 且 ,
所以 ,所以 ,
即证: ,
即证: ,
即证: ,
记 ,
则 ,
所以 在 为增函数,所以
所以 ,
设 ,
则 ,
所以 在 上是增函数,
所以
所以 ,
即所以若 ,则 .(12分)
22. 【解析】(1)把 , 代入 ,
得曲线 的极坐标方程为 ,即 .(2分)将 中的参数消去,得曲线 的普通方程为 ,
把 , 代入,得曲线 的极坐标方程为 ,即 .(5分)
(2)由题得 , , ,
,(7分)
因为 ,所以
,
其中 , ,
当 ,即 时, 的面积取得最大值 .(10分)
23.【解析】(1)函数 的最小值为 ,此时 ,(1分)
当 时, ,
当 时, ,
当 时, ,
函数 ,(3分)
函数在 上单调递减,在 上单调递增,
当 时, ,
所以函数 的最小值为 ,
故 .(5分)(2)由(1)知 , ,
因为 , ,
所以 , , , , ,(7分)
又因为 ,
所以 ,又 ,所以 ,所以 .所以 .(10分)公众号:高中试卷君