文档内容
2024届新高三开学摸底考试卷(全国卷)
理科数学02•全解全析
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一个选项是符合题目要求的.
1.已知集合 , ,则 ( )
A. B.
C. D.
【答案】B
【详解】由 ,可得 ,所以 ,
所以 ,
又 ,所以 .
故选:B.
2.若 , ,则 ( )
A. B. C.2 D.10
【答案】A
【详解】 ,
所以 ,
故选:A.
3.已知函数 ,则 ( )
A.4 B.5 C.6 D.7
【答案】D
【分析】结合函数的解析式及对数的运算性质计算即可.【详解】由题意可得
,
故选:D.
4.足球运动是深受人们喜爱的一项体育运动,某次传球训练中,教练员让甲、乙、丙、
丁4名球员进行传接球训练,从甲开始传球,等可能地传给另外3人中的1人,接球
者再等可能地传给另外3人中的1人,如此一直进行.假设每个球都能被接住,若第4
次传球后,球又恰好回到甲脚下,则不同的传球方法为( )
A.18种 B.21种 C.27种 D.45种
【答案】B
【分析】根据题意分为两种情况讨论:①第一次甲将球传给其余三人,第二次将球传
给甲,第三次甲再传给其余三人,第四次再将球传给甲;②第一次甲将球传给其余三
人,第二次将球传给甲之外的2人,第三次依然将球传给除甲之外的2人,第四次再
将球传给甲,结合分类计数原理,即可求解.
【详解】根据题意,分为两种情况讨论:
①第一次甲将球传给其余三人,有 种情况,第二次将球传给甲,第三次甲再传
给其余三人,有 种情况,第四次再将球传给甲,此时共有 种情况;
②第一次甲将球传给其余三人,有 种情况,
第二次将球传给甲之外的2人,有 种情况,
第三次依然将球传给除甲之外的2人,有 种情况,
第四次再将球传给甲,有1中情况,
此时共有 种情况,
由分类计算原理可得,第四次传球后,求又回到甲的脚下的传球方式,共有
种.
故选:B.
5.“埃拉托塞尼筛法”是保证能够挑选全部素数的一种古老的方法.这种方法是依次
写出2和2以上的自然数,留下第一个数2不动,剔除掉所有2的倍数;接着,在剩余
的数中2后面的一个数3不动,剔除掉所有3的倍数;接下来,再在剩余的数中对3后
面的一个数5作同样处理;……,依次进行同样的剔除.剔除到最后,剩下的便全是素
数.在利用“埃拉托塞尼筛法”挑选2到20的全部素数过程中剔除的所有数的和为(
)
A.130 B.132 C.134 D.141
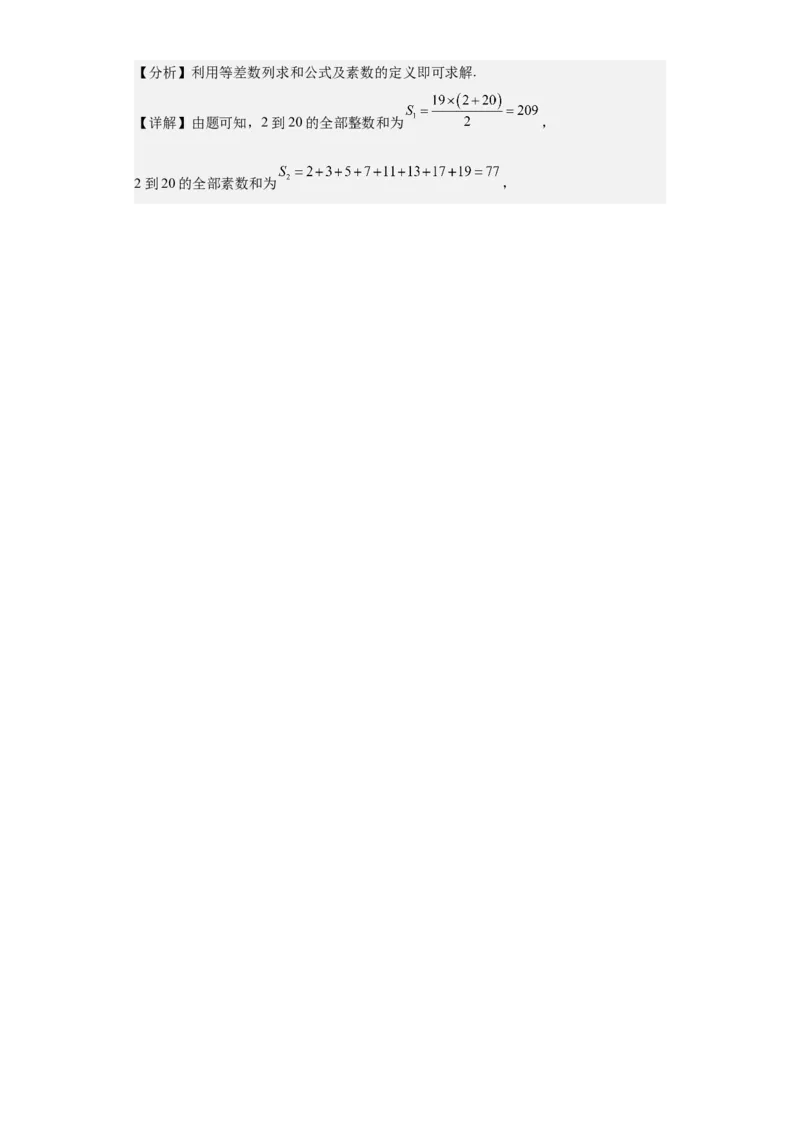
【答案】B【分析】利用等差数列求和公式及素数的定义即可求解.
【详解】由题可知,2到20的全部整数和为 ,
2到20的全部素数和为 ,所以挑选2到20的全部素数过程中剔除的所有数的和为 .
故选:B.
6.已知函数 的最小正周期为T,且 ,若
的图象关于直线 对称,则 ( )
A. B. C. D.
【答案】A
【分析】运用二倍角公式化简 ,结合 与 的对称性求得 的值,进
而求得结果.
【详解】因为 ,
所以 .
又因为 ,
所以 ,即 ,①
又因为 的图象关于直线 对称,
所以 , .
所以 , ,②
所以由①②得 ,
所以 ,
故 .
故选:A.
7.在三角形 中, 和 分别是 边上的高和中线,则 ( )
A.14 B.15 C.16 D.17
【答案】C
【分析】将 作为基底,用基底表示 和 ,根据数量积的规则计算即可.【详解】
设 ,则有
,
由余弦定理得 ,
,
其中 , ,解得 ,
;
故选:C.
8.平行四边形 中,点 在边 上, ,记 ,则
( )
A. B.
C. D.
【答案】D
【分析】根据给定的几何图形,结合向量的线性运算求解作答.
【详解】在 中, , ,
所以 .
故选:D
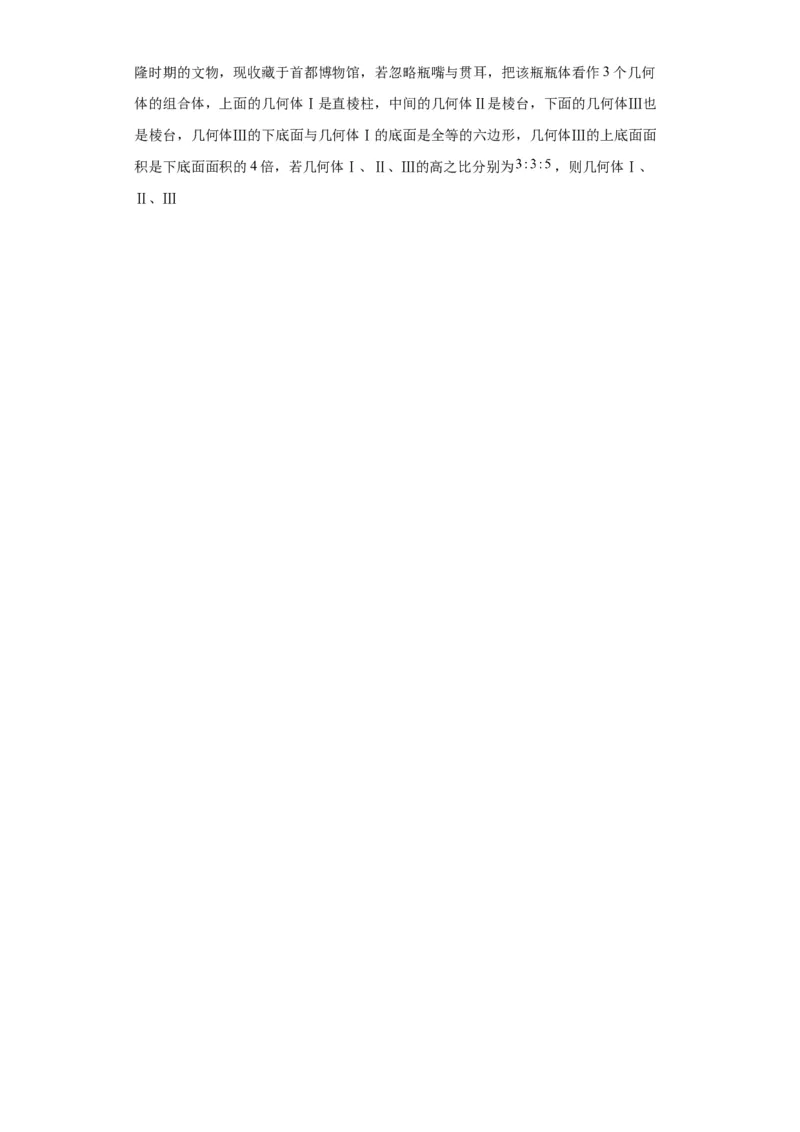
9.贯耳瓶流行于宋代,清代亦有仿制,如图所示的青花折枝花卉纹六方贯耳瓶是清乾隆时期的文物,现收藏于首都博物馆,若忽略瓶嘴与贯耳,把该瓶瓶体看作3个几何
体的组合体,上面的几何体Ⅰ是直棱柱,中间的几何体Ⅱ是棱台,下面的几何体Ⅲ也
是棱台,几何体Ⅲ的下底面与几何体Ⅰ的底面是全等的六边形,几何体Ⅲ的上底面面
积是下底面面积的4倍,若几何体Ⅰ、Ⅱ、Ⅲ的高之比分别为 ,则几何体Ⅰ、
Ⅱ、Ⅲ的体积之比为( )
A. B. C. D.
【答案】D
【分析】设上面的六棱柱的底面面积为S,高为 ,根据棱柱和棱台的体积公式直接
计算,然后求比可得.
【详解】设上面的六棱柱的底面面积为S,高为 ,由上到下的三个几何体体积分别
记为 ,
则 ,
,
,
所以
故选:D
10.已知过双曲线 : 的右焦点 作 轴的垂线与两条渐
近线交于 , , 的面积为 ,则该双曲线的离心率为( )
A. B. C.2 D.
【答案】A【分析】先结合双曲线的渐近线方程求出 ,再根据三角形面积公式得到
即可.【详解】
由题知,双曲线的渐近线为 ,
得 , ,
,
,
,
故选:A.
11.已知直线 上的两点 ,且 ,点 为圆
上任一点,则 的面积的最大值为( )
A. B. C. D.
【答案】A
【分析】找到圆上的点到直线距离的最大值作为 的高,再由面积公式求解即可.
【详解】把圆 变形为 ,
则圆心 ,半径 ,
圆心 到直线 的距离 ,
则圆 上的点到直线 的距离的最大值为 ,又 ,∴ 的面积的最大值为 .
故选:A.
12.已知 是函数 的导函数,对于任意的 都有
,且 ,则不等式 的解集是( )A. B.
C. D.
【答案】D
【分析】法一、构造常函数 计算即可;法二、构造 ,利
用条件判断其单调性解不等式即可.
【详解】法一:构造特殊函数.令 ,则 满足题目条件,
把 代入 得 解得 ,
故选: .
法二:构造辅助函数.令 ,则 ,
所以 在 上单调递增,
又因为 ,所以 ,所以 ,
故选:D.
二、填空题:本题共4小题,每小题5分,共20分.
13.某机器生产的产品质量误差 是 的第60个百分
位数,则 __________.
附:若 ,则 ,
【答案】
【分析】先根据百分位数的求法得t,然后根据正态分布概率公式可得.
【详解】因为 ,所以 ,
由 可知
所以 .故答案为:
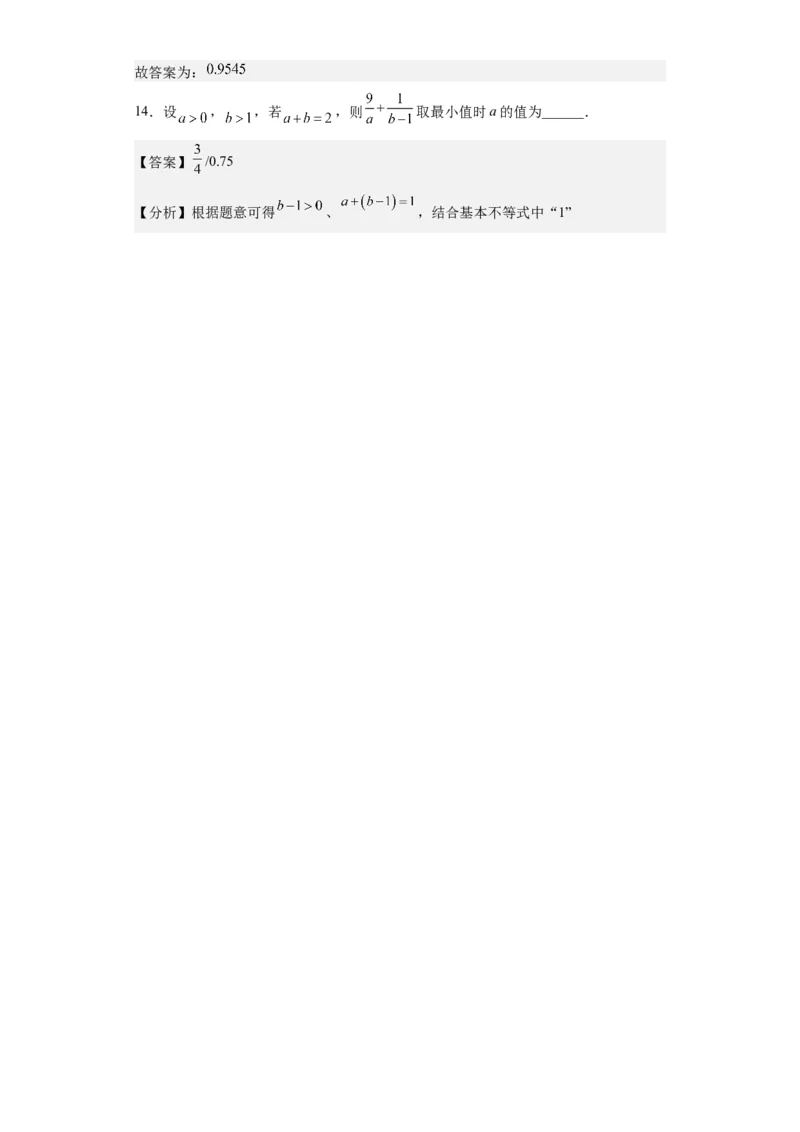
14.设 , ,若 ,则 取最小值时a的值为______.
【答案】 /0.75
【分析】根据题意可得 、 ,结合基本不等式中“1”的用法计算即可求解.
【详解】由 , ,得 ,
由 ,得 ,
∴ ,
当且仅当 即 , 时等号成立.
故当 , 时 取得最小值16.
故答案为: .
15.设抛物线 : ( )焦点为 ,准线为 ,过第一象限内的抛物线上
一点 作 的垂线,垂足为 .设 , 与 相交于 .若 ,且
的面积为 ,则抛物线的方程为________________.
【答案】
【分析】由抛物线定义可得四边形 为平行四边形,故 可得点
即得抛物线方程.
【详解】如图所示, , .
所以 .轴, , ,
所以四边形 为平行四边形,
, .
,解得 ,
代入 可取 ,,
解得 . .
故答案为: .
16.如图,在三棱锥 中, ,若该三
棱锥的外接球表面积为 ,则锐二面角 的平面角的正切值为__________.
【答案】 /
【分析】三棱锥的外接球球心位于过三角形 , 的外接圆圆心且与此平面垂直
的直线上,找到球心再结合锐二面角 的平面角的定义进行求解.
【详解】如图,
因为 ,所以该三棱锥的外接球半径 ,
已知 ,由余弦定理可得 ,所以
,同理可证 .
所以 的外接圆圆心 分别位于斜边 的中点,
设球心为 ,则 平面 , 平面 , 平面 ,
所以 ,因为 ,
所以 ,
同理可证 ,因为 ,所以 ,
设锐二面角 的平面角为 ,因为 平面 ,所以 与 互余,即 , ,故答案为: .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必
考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
17.已知数列 和 满足 .
(1)证明: 和 都是等比数列;
(2)求 的前 项和 .
【答案】(1)证明见解析
(2)
【分析】(1)由 , 两式相加、相减,结合等比数列的定义即
可证明;
(2)由(1)可得 , ,即可求出 和 的通项公式,
从而得到 ,再利用分组求和法及等边数列求和公式计算可得.
【详解】(1)因为 , ,
所以 , ,
又由 , 得 , ,
所以数列 是首项为 ,公比为 的等比数列,数列 是首项为 ,公比为 的等比数列.
(2)由(1)得 , ,
所以 , ,所以 ,
所以 .
18.如图,四边形 为菱形, 平面 , , .
(1)证明:平面 平面 ;
(2)若 ,求二面角 的大小.
【答案】(1)证明见解析
(2)
【分析】(1)根据线面垂直得线线垂直,进而由线段的长度得勾股定理,证明线线垂
直,即可得线面垂直证明面面垂直.
(2)建立空间直角坐标系,利用法向量的夹角即可求解二面角大小.
【详解】(1)设BD交AC于点O,连接EO,FO,
因为四边形ABCD为菱形,所以 .
因为ED 平面ABCD,AC 平面ABCD,所以 .
又 , 平面BDEF,所以 平面BDEF;
又 平面BDEF,所以 .
设FB=1,由题意得ED=2, .
因为FB//ED,且 面 ,则FB 平面ABCD,
而 平面ABCD,故 , ,
所以 , , .因为 ,所以 .
因为 , 平面ACF,所以EO 平面ACF.又EO 平面EAC,所以平面EAC 平面FAC.
(2)取EF中点G,连接OG,所以OG//ED,OG 底面ABCD.
以O为原点,以 分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
因为 ,由(1)中所设知, ,
所以, ,
所以 .
所以 , , ,
设平面FAE的一个法向量为 ,
则 ,
所以 ;
平面AEC的一个法向量为 ,
则 ,
所以 ;
所以 ,
由图形可知二面角 的平面角为锐角,
所以二面角 的大小为 .19.某购物中心准备进行扩大规模,在制定末来发展策略时,对中心的现有顾客满意度进行了一个初步的现场调查,分别调查顾客对
购物中心的商品质量、服务质量、购物环境、广告宣传的满意程度.调查时将对被抽
中的每个顾客从这四个问题中随机抽取两个问题来提问,统计顾客的满意情况.假设,
有三名顾客被抽到,且这三名顾客对这四个问题的满意情况如下表:
商品质量 服务质量 购物环境 广告宣传
顾客
满意 不满意 满意 不满意
甲
顾客
不满意 满意 满意 满意
乙
顾客
满意 满意 满意 不满意
丙
每得到一个满意加10分,最终以总得分作为制定发展策略的参考依据.
(1)求购物中心得分为50分的概率;
(2)若已知购物中心得分为50分,则顾客丙投出一个不满意的概率为多少?
(3)列出该购物中心得到满意的个数X的分布列,并求得分 的数学期望.
【答案】(1)
(2)
(3)分布列见解析,40
【分析】(1)得分为50分即在六个问题的结果中,有五个满意,一个不满意,然后
按照古典概型的概率进行计算;
(2)由条件概率的公式进行计算即可;
(3)按求分布列的步骤进行计算,进而可得数学期望.
【详解】(1)将得分为50分记为事件A;得分为50分即在六个问题的结果中,有五
个满意,一个不满意,
可能的结果共有: (种)
三名顾客产生的反馈结果总共有: (种)
则 ,∴购物中心得分为50分的概率为
(2)将顾客丙投出一个不满意记为事件B,则, ,
(3) 可能的取值为2、3、4、5、6
,,
2 3 4 5 6
∵ ,∴ .
20.已知椭圆C: 的左、右顶点分别为 , ,
右焦点为 ,O为坐标原点,OB的中点为D(D在 的左方), .
(1)求椭圆C的标准方程;
(2)设过点D且斜率不为0的直线与椭圆C交于M,N两点,设直线AM,AN的斜率分
别是 , ,试问 是否为定值?若是,求出定值;若不是,请说明理由.
【答案】(1)
(2) 是定值,定值为 .
【分析】(1)根据椭圆的几何性质求出 ,可得椭圆的标准方程;
(2)设过点D且斜率不为0的直线方程为 ,代入 ,设
, ,根据韦达定理得 和 ,再利用斜率公式得 ,代入
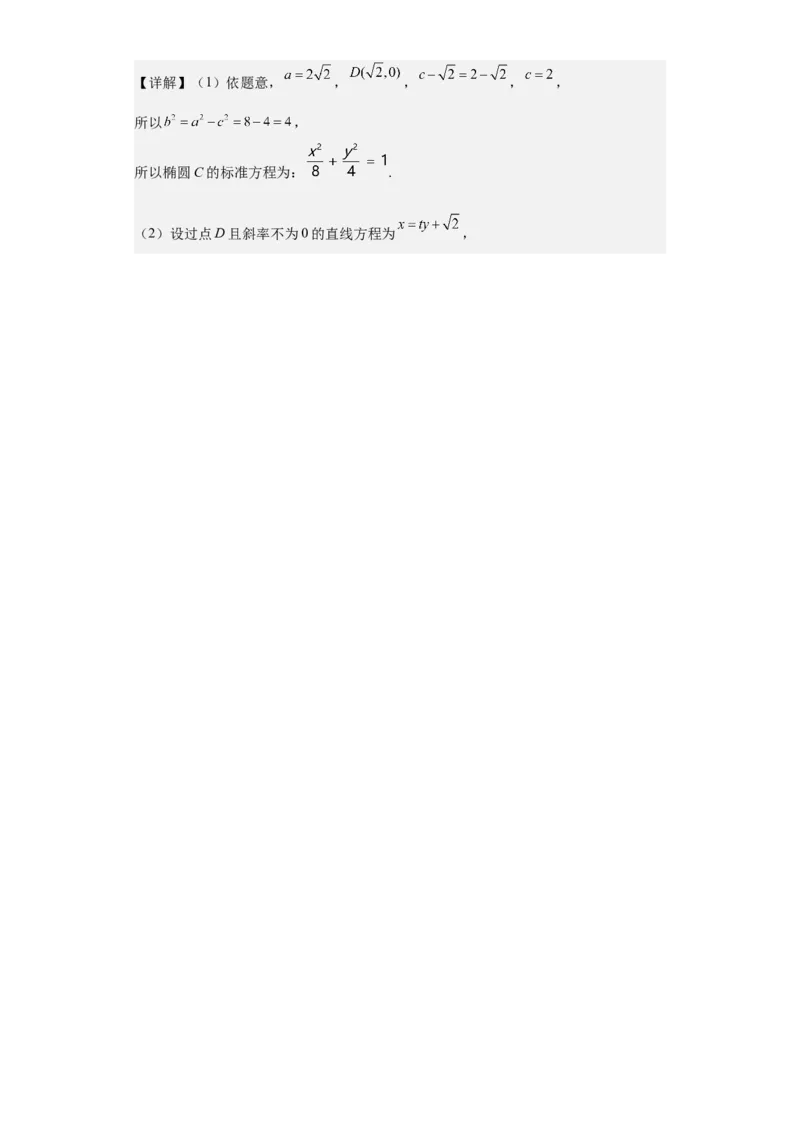
和 ,化简可得 .【详解】(1)依题意, , , , ,
所以 ,
所以椭圆C的标准方程为: .
(2)设过点D且斜率不为0的直线方程为 ,联立 ,消去 并整理得 ,
,
设 , ,
则 , ,
所以
.
所以 为定值 .
21.已知函数 .
(1)若 ,求 在点 处的切线方程;
(2)若 是 的两个极值点,证明: .
【答案】(1) ;(2)证明见解析
【分析】(1)求导,计算切点处的函数值与导数值,根据点斜式即可求解切线方程;
(2)根据极值点的定义,可得 是方程的两个不等的正实根,根据韦达定理代入化简,将问题转化成 ,令
,构造函数 ,结合导数证明即可.
【详解】(1)当 时, ,则 ,
所以 , ,
所以 在点 处的切线方程为 ,
即
(2)证明:由 ,可知 ,
因为 ( )是 的极值点,
所以 方程 的两个不等的正实数根,
所以 , ,
则
.
要证 成立,
只需证 ,即证 ,
即证 ,即证 ,
设 ,则 ,即证 ,
令 ,
则 ,所以 在 上单调递减,则 ,
所以 ,故 .
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所
做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)在极坐标系中,曲线 的极坐标方程为 ,以极点为坐标原点,极轴
为 轴正半轴,建立直角坐标系,曲线 的参数方程为 ( 为参数).
(1)写出 的直角坐标方程和 的普通方程;
(2)已知点 , 与 相交于 , 两点,求 的值.
【答案】(1)曲线 的直角坐标方程为 ,曲线 的普通方程为 ;
(2) .
【分析】(1)把曲线 化为 ,即得曲线 的直角坐标方程,
把参数方程平方相加得曲线 的普通方程;
(2)求出曲线 的参数方程,联立曲线 的参数方程与曲线 的普通方程得
,再利用直线参数方程 的几何意义求解.
【详解】(1)曲线 的极坐标方程为 ,即
,
则曲线 的直角坐标方程为 ,
把参数方程平方相加得曲线 的普通方程为 .
(2)易知点 在直线 上,且该直线的斜率为 ,倾斜角为 ,则曲线 的参数方程为 ( 为参数),
联立曲线 的参数方程与曲线 的普通方程得 ,
设点 , 在直线 上对应的参数分别为 , ,
由韦达定理可得 , ,
.
23.[选修4-5:不等式选讲](10分)
已知函数 .(1)求 的最小值 ;
(2)若 为正实数,且 ,证明不等式 .
【答案】(1)
(2)证明见解析
【分析】(1)将函数写成分段函数,结合函数图象求解即可;
(2)解法一:根据基本不等式“1”的用法分析证明;解法二:利用柯西不等式直接证
明即可.
【详解】(1)由题知 ,
其函数图象如图所示,
所以, .
(2)由(1)可知 ,则 ,
解法一:利用基本不等式:
,
当且仅当 时取等号.
所以, .
解法二:利用柯西不等式:,
当且仅当 时取等号.所以, .公众号:高中试卷君