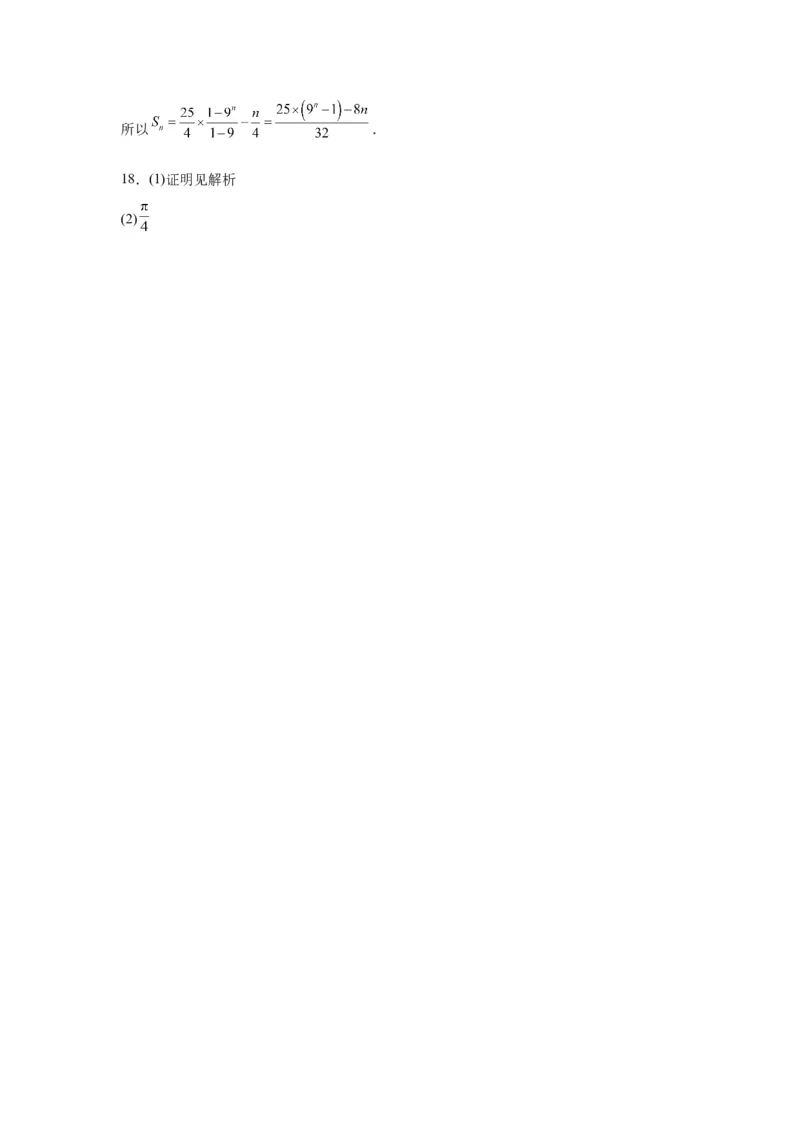
文档内容
2024届新高三开学摸底考试卷(全国卷)
理科数学·参考答案02
1 2 3 4 5 6 7 8 9 10 11 12
B A D B B A C D D A A D
13.
14. /0.75
15.
16. /
17.(1)证明见解析
(2)
【详解】(1)因为 , ,
所以 , ,
又由 , 得 , ,
所以数列 是首项为 ,公比为 的等比数列,
数列 是首项为 ,公比为 的等比数列.
(2)由(1)得 , ,
所以 , ,
所以 ,所以 .
18.(1)证明见解析
(2)【详解】(1)设BD交AC于点O,连接EO,FO,
因为四边形ABCD为菱形,所以 .
因为ED 平面ABCD,AC 平面ABCD,所以 .
又 , 平面BDEF,所以 平面BDEF;
又 平面BDEF,所以 .
设FB=1,由题意得ED=2, .
因为FB//ED,且 面 ,则FB 平面ABCD,
而 平面ABCD,故 , ,
所以 , , .
因为 ,所以 .
因为 , 平面ACF,所以EO 平面ACF.
又EO 平面EAC,所以平面EAC 平面FAC.
(2)取EF中点G,连接OG,所以OG//ED,OG 底面ABCD.
以O为原点,以 分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
因为 ,由(1)中所设知, ,
所以, ,
所以 .
所以 , , ,
设平面FAE的一个法向量为 ,
则 ,
所以 ;平面AEC的一个法向量为 ,
则 ,所以 ;
所以 ,
由图形可知二面角 的平面角为锐角,
所以二面角 的大小为 .
19.(1)
(2)
(3)分布列见解析,40
【详解】(1)将得分为50分记为事件A;得分为50分即在六个问题的结果中,有五个满
意,一个不满意,
可能的结果共有: (种)
三名顾客产生的反馈结果总共有: (种)
则 ,∴购物中心得分为50分的概率为
(2)将顾客丙投出一个不满意记为事件B,则
, ,
(3) 可能的取值为2、3、4、5、6,
,2 3 4 5 6
∵ ,∴ .
20.(1)
(2) 是定值,定值为 .
【详解】(1)依题意, , , , ,
所以 ,
所以椭圆C的标准方程为: .
(2)设过点D且斜率不为0的直线方程为 ,
联立 ,消去 并整理得 ,
,
设 , ,则 , ,
所以.
所以 为定值 .
21.(1) ;
(2)证明见解析
【详解】(1)当 时, ,则 ,
所以 , ,
所以 在点 处的切线方程为 ,
即
(2)证明:由 ,可知 ,
因为 ( )是 的极值点,
所以 方程 的两个不等的正实数根,
所以 , ,
则
.要证 成立,
只需证 ,即证 ,
即证 ,即证 ,设 ,则 ,即证 ,
令 ,
则 ,
所以 在 上单调递减,则 ,
所以 ,故 .
22.(1)曲线 的直角坐标方程为 ,曲线 的普通方程为 ;
(2) .
【详解】(1)曲线 的极坐标方程为 ,即 ,
则曲线 的直角坐标方程为 ,
把参数方程平方相加得曲线 的普通方程为 .
(2)易知点 在直线 上,且该直线的斜率为 ,倾斜角为 ,
则曲线 的参数方程为 ( 为参数),
联立曲线 的参数方程与曲线 的普通方程得 ,
设点 , 在直线 上对应的参数分别为 , ,
由韦达定理可得 , ,
.23.(1)
(2)证明见解析
【详解】(1)由题知 ,其函数图象如图所示,
所以, .
(2)由(1)可知 ,则 ,
解法一:利用基本不等式:
,
当且仅当 时取等号.
所以, .
解法二:利用柯西不等式:
,
当且仅当 时取等号.
所以, .公众号:高中试卷君