大庆市2026届高三年级第二次教学质量检测数学答案(1)_2026年1月_260112黑龙江大庆市2026届高三年级第二次教学质量检测（全科）

大庆市 2026 届高三年级第二次教学质量检测 数学答案及评分标准 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一 项是符合题目要求的。 1 2 3 4 5 6 7 8 B A A D B C B D 1.【解析】复数z满足z 1i，则 z  12  (1)2  2 .故选：B. 2.【解析】因为函数 f(t)2t在R上单调递增，所以2x 2y  x y， 所以“x y0”是“2x 2y”的充分不必要条件，故选：A 3.【解析】因为ylog (x1)的定义域为  x x1  ，所以AB={x|1 x4}.故选：A 2 4.【解析】因为a  1,2,b   3,1， 所以a  b  4,1，a  b  13,2.           因为(ab) ab ，所以(ab) ab 0 6 所以4131(2)0.解得 .故选：D. 11 3 5.【解析】因为 OP  3242 5，所以cos . 5 π  3 7 所以sin 2cos22cos212( )2 1 .故选：B 2  5 25 a 6.【解析】由 2025 1得a a 0，因为a 0，所以d 0，所以a 0，a 0 a 2025 2026 1 2025 2026 2026 a 由 2025 1和a 0得a a 0， a 2026 2025 2026 2026 4050a a  所以S  1 4050  2025 a a  0 ， 4050 2 2025 2026 4051a a  S  1 4051  4051a  0， 4051 2 2026 故使得S 0的n的最小值为4051.故选：C n 7.【解析】因为 f(x1)是偶函数，所以 f x1 f x1，所以 f  x2  f x  ， 因为 f x是定义在R上的奇函数，所以 f xf x， 所以 f x2f x ，所以 f x4f x2 f x，所以函数 f x以4为周期 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}所以 f 2024 f 5064 f 0000， f 2025 f 50641 f 1112 f 2026 f 50642 f 2 f(0)0 所以 f 2024 f 2025 f 20262. 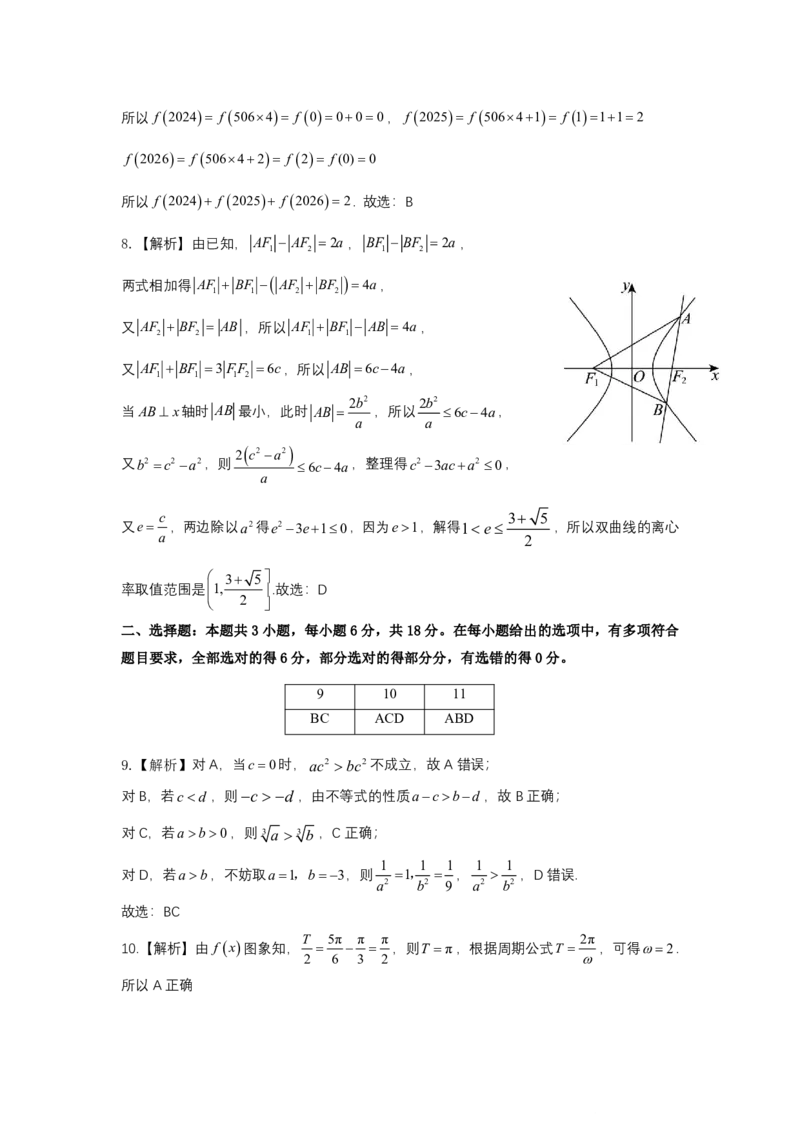故选：B 8.【解析】由已知， AF  AF  2a ， BF  BF  2a ， 1 2 1 2 两式相加得 AF  BF  AF  BF 4a， 1 1 2 2 又 AF  BF  AB ，所以 AF  BF  AB 4a， 2 2 1 1 又 AF  BF 3FF 6c，所以 AB 6c4a， 1 1 1 2 2b2 2b2 当ABx轴时 AB 最小，此时 AB  ，所以 6c4a， a a 2  c2a2 又b2 c2a2，则 6c4a ，整理得c23aca2 0， a c 3 5 又e ，两边除以a2得e23e10，因为e1，解得1e ，所以双曲线的离心 a 2  3 5 率取值范围是1, .故选：D   2  二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合 题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分。 9 10 11 BC ACD ABD 9.【解析】对A，当c0时，ac2 bc2不成立，故A错误； 对B，若cd，则c  d ，由不等式的性质acbd ，故B正确； 对C，若ab0，则 3 a  3 b ，C正确； 1 1 1 1 1 对D，若ab，不妨取a1，b3，则 1，  ，  ，D错误. a2 b2 9 a2 b2 故选：BC T 5π π π 2π 10.【解析】由 f x图象知，    ，则T π，根据周期公式T  ，可得2. 2 6 3 2  所以A正确 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}3(1) 3(1) 又因为函数 f x的最大值为3，最小值为1，所以A 2,b 1. 2 2 π  π  π 代入 ,1得2cos(2 )11，因为 ，所以 . 3  3 2 3 π 所以 f(x)2cos(2x )1. 3 π π kπ 令2x kπ,kZ可得对称轴方程x  ,kZ， 3 6 2  1 当x 时k= Z，故B不正确。 12 2 π π 1 C：因为x ,x 是 f x的两个零点，令 f(x)2cos(2x )10，则cos(2x ) ， 1 2 3 3 2 π 2π π 4π 所以2x 2kπ ,kZ或2x 2kπ ,kZ， 3 3 3 3 π π 解得xkπ+ ,kZ，或xkπ+ ,kZ， 6 2 π π π 根据题意，取x kπ+ ,k Z，x k π+ ,k Z，所以|x x ||(k k )π+ |,k ,k Z， 1 1 6 1 2 2 2 2 1 2 1 2 3 1 2 π 当k k 0时，|x x | ，故C正确. 1 2 1 2 3 π π π π D：由C知 f(x)在0,上的10个零点依次为： ， ，， 4π， 4π. 6 2 6 2 π 9π 由 f x在区间0,m  上至少有10个零点，则m4π+  . 2 2 9π 所以m的最小值为 ，故D正确； 2 故选：ACD. 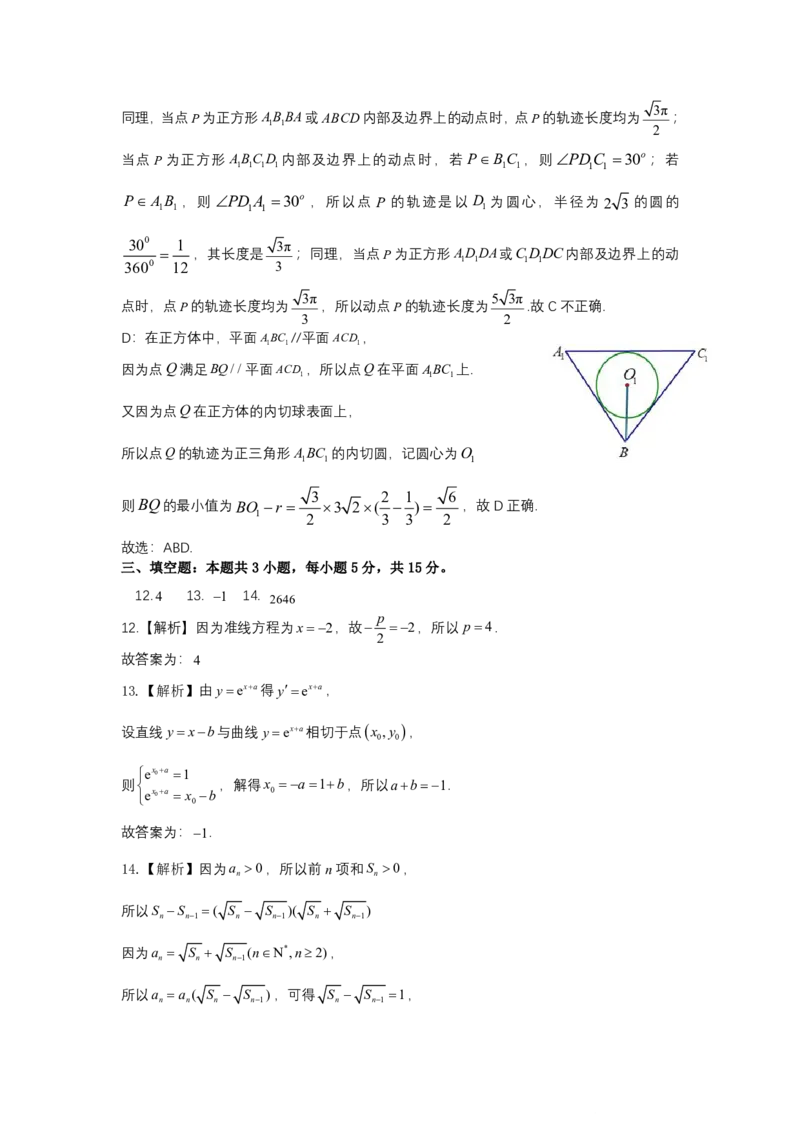11.【解析】A：在正方体ABCDAB C D 中，CD //AB ， 1 1 1 1 1 1 AB平面ABC ，CD 平面ABC ，所以CD //平面ABC ，故A正确 1 1 1 1 1 1 1 1 1 B：三棱锥A BDC 与正方体ABCDAB C D 有相同的外接球， 1 1 1 1 1 1 3 3 所以外接球的半径R ，所以S 4R2 27，故B正确； 2 C：因为DC 平面BCCB ，C P平面BCCB ，所以DC CP， 1 1 1 1 1 1 1 1 1 1 因为DP2 3，DC 3，所以 CP DP2CD2  3， 1 1 1 1 1 1 1 1 3π 所以点P的运动轨迹是以C 为圆心，半径为 3的圆的 ，其长度是 ； 1 4 2 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}3π 同理，当点P为正方形ABBA或ABCD内部及边界上的动点时，点P的轨迹长度均为 ； 1 1 2 当点P为正方形 ABCD 内部及边界上的动点时，若 PBC ，则PDC 30o ；若 1 1 1 1 1 1 1 1 P AB ，则 PD A 30o ，所以点 P 的轨迹是以 D 为圆心，半径为 2 3 的圆的 1 1 1 1 1 300 1 3π  ，其长度是 ；同理，当点P为正方形ADDA或CDDC内部及边界上的动 3600 12 3 1 1 1 1 3π 5 3π 点时，点P的轨迹长度均为 ，所以动点P的轨迹长度为 .故C不正确. 3 2 D：在正方体中，平面ABC //平面ACD ， 1 1 1 因为点Q满足BQ//平面ACD ，所以点Q在平面ABC 上. 1 1 1 又因为点Q在正方体的内切球表面上， 所以点Q的轨迹为正三角形ABC 的内切圆，记圆心为O 1 1 1 3 2 1 6 则BQ的最小值为BO r  3 2(  ) ，故D正确. 1 2 3 3 2 故选：ABD. 三、填空题：本题共3小题，每小题5分，共15分。 12.4 13. 1 14. 2646 p 12.【解析】因为准线方程为x2，故 2，所以 p4. 2 故答案为：4 13.【解析】由yexa得yexa， 设直线yxb与曲线yexa相切于点x ,y ， 0 0 ex0 a 1 则 ，解得x a1b，所以ab1. ex0 a  x b 0 0 故答案为：1. 14.【解析】因为a 0，所以前n项和S 0， n n 所以S S ( S  S )( S  S ) n n1 n n1 n n1 因为a  S  S (nN*,n2)， n n n1 所以a a ( S  S )，可得 S  S 1， n n n n1 n n1 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}所以数列  S  是首项和公差均为1的等差数列，所以 S n，即S n2， n n n 当n2时，a S S n2(n1)2 2n1， n n n1 又a 1满足上式，所以a 2n1(nN*). 1 n k11k1 新数列b 中从a 到a 共有k112k 项， n 1 k1 2 k1k2 当k 62时， 2016， 2 ， 2026  b  a a a 1 2 2  3 3 62 62  2026 2016  63 i 1 2 63 i1 ， (1125)63  122 32 622 1063 2       ， 6363 12 22  32 42  612 622 1063 . 16262 3969 10632646 2 故答案为：2646 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15.(本小题满分13分) 3 解：（1）由正弦定理得：sinBcosA sinBsinAsinC， 3 在三角形中CπAB，所以sinBcosA 3 sinBsinAsin AB ， 3 3 即sinBcosA sinBsinAsinAcosBcosAsinB， 3 因为A0,π,sinA0，所以tanB 3， π 因为B0,π，所以B .....................................................................................................................6分 3 1 3 （2）S  acsinB ac 3，所以ac4， △ABC 2 4 由余弦定理得b2 a2c22accosB(ac)23ac361224，所以b2 6， 所以ABC的周长为62 6 ............................................................................................................13分 16.(本小题满分15分) 解：（1）因为a 2a 2，a 2所以b 0 n1 n 1 n {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}b a 2 2a 4 因为 n1  n1  n 2， b a 2 a 2 n n n 所以数列b 是以b a 24为首项，2为公比的等比数列． n 1 1 所以b 42n1，所以数列b 的通项公式为b 2n1；............................................................6分 n n n 1 1 1 1 （2）由c  得c    n log b log b n (n1)(n2) n1 n2 2 n 2 n1 1 1 1 1 1 1 1 1 1 所以T          n 2 3 3 4 n1 n2 2 n2 2 1 1 1 因为数列T 为单调递增数列，所以T T，T    n n 1 1 2 3 6 1 1 所以 T  .......................................................................................................................15分 6 n 2 17.(本小题满分15分) 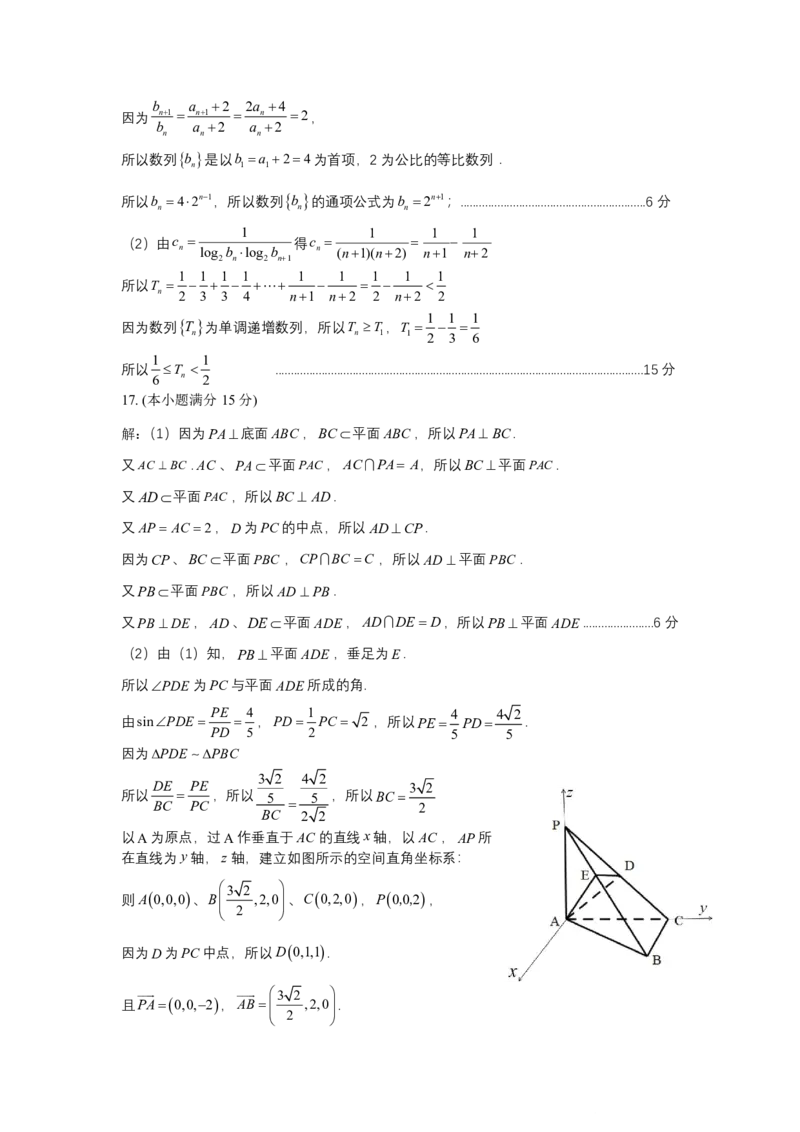解：（1）因为PA底面ABC，BC平面ABC，所以PABC. 又AC BC .AC、PA平面PAC，ACPA A，所以BC平面PAC. 又AD平面PAC，所以BC AD. 又AP AC 2，D为PC的中点，所以ADCP. 因为CP、BC平面PBC ，CPBC C ，所以AD平面PBC . 又PB平面PBC ，所以ADPB. 又PBDE，AD、DE平面ADE，ADDED，所以PB平面ADE.......................6分 （2）由（1）知，PB平面ADE，垂足为E. 所以PDE为PC与平面ADE所成的角. PE 4 1 4 4 2 由sinPDE   ，PD PC  2 ，所以PE PD . PD 5 2 5 5 因为PDE PBC 3 2 4 2 DE PE 3 2 所以  ，所以 5 5 ，所以BC  BC PC  2 BC 2 2 以A为原点，过A作垂直于AC的直线x轴，以AC，AP所 在直线为y轴，z轴，建立如图所示的空间直角坐标系： 3 2  则A0,0,0、B ,2,0、C0,2,0，P0,0,2，    2  因为D为PC中点，所以D0,1,1.   3 2  且PA0,0,2，AB ,2,0.    2  {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#} 设平面PAB的一个法向量为mx,y,z，   mPA2z0     则   3 2 ，取x2 2，则m 2 2,3,0 ， mAB x2y0  2  平面PBC 的一个法向量可取AD0,1,1. 设平面PAB与平面PBC 的夹角为，   mDE 3 3 34 则cos     ， m  DE 17 2 34 3 34 故平面PAB与平面PBC 夹角的余弦值为 .............................................................15分 34 18.(本小题满分17分) c1  b2 2 x2 （1）由题意可知  ，解得a 2,b1，所以椭圆C的方程为 y2 1......4分  a 2 2 a2 b2 c2  2 （2）易知过点P且与椭圆相切的直线斜率存在，因此可设该直线方程为yk(x1) . 2  2 联立直线与椭圆   yk(x1) 2 ,整理得  12k2 x2  2 2k4k2  x  2k22 2k1  0 ，  x22y220 2 令0，整理得2k22 2k10，解得k . 2 2 所以过点P的切线方程为：y x 2 ， 2 再令 y 0，得x 2.所以点Q的坐标为(2,0). 由已知经过点Q的直线AB的斜率不为0，设直线方程为xty2,A(x,y ),B(x ,y ) 1 1 2 2 xty2 联立直线与椭圆 ,整理得  t22  y24ty20 x22y220 令16t2 8(t2 2)0解得t2  2 4t 2 y  y  ,y y  1 2 t22 1 2 t22 8t2 16 因为 AB  1t2 y  y  1t2 (y  y )2 4y y  1t2 1 2 1 2 1 2 t2 2 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}2 点O到直线AB的距离d  ， 1t2 1 2 8t2 16 t2 2 所以S  1t2 2 2 OAB 2 1t2 t2 2 t2 2 u 2 2 2 S 2 2   令u t22(u0)，则 OAB u2 4 u 4 2 ，当且仅当t  6时S OAB 取 u 2 到最大值为 ； ...................................................................................................................10分 2 （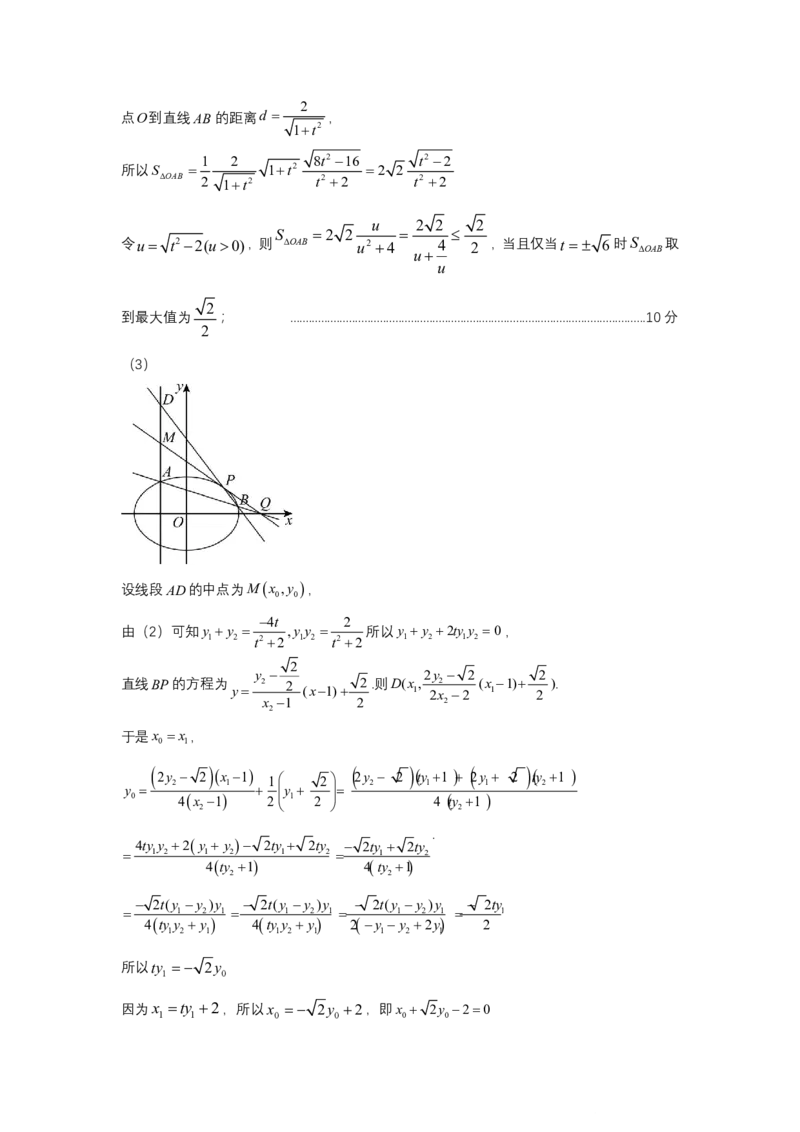3） 设线段AD的中点为Mx ,y ， 0 0 4t 2 由（2）可知y y  ,y y  所以y y 2ty y 0， 1 2 t22 1 2 t22 1 2 1 2 2 y  2y  2 2 直线BP的方程为 2 2 2 .则D(x, 2 (x 1) ). y (x1) 1 2x 2 1 2 x 1 2 2 2 于是x x ， 0 1  2y 2  2 x 1 1 1 2  2y 2  2 ty 1 1   2y 1  2  ty 2 1  y   y   0 4x 1 2   1 2   4 ty 1  2 2 . 4ty y 2y  y  2ty  2ty  2ty  2ty  1 2 1 2 1 2  1 2 4ty 1 4ty 1 2 2  2t(y y )y  2t(y y )y  2t(y y )y  2ty  1 2 1  1 2 1  1 2 1  1 4ty y  y  4ty y  y 2 y  y 2y 2 1 2 1 1 2 1 1 2 1 所以ty   2y 1 0 因为x ty 2，所以x   2y 2，即x  2y 20 1 1 0 0 0 0 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}因此点Mx ,y 在直线x 2y20上，即线段AD中点在定直线x 2y20上. 0 0 ........................................................................................................................................................................17分 19.(本小题满分17分) 解：（1）函数 f xlnxaxxaR有两个不同的零点， lnx 所以 f xlnxaxx0，即a 1有两个不同的解， x lnx 1lnx 令gx 1x0，由gx 0得xe， x x2 当0xe时，gx0，所以gx在(0,e)上单调递增， 当xe时，gx0，所以gx在(e,+)上单调递减， 1 所以gx ge 1， max e lnx 当x0时，g  x ；当x时， 0,g  x 1 x  1  所以a1a 1. ........................................................................................................................4分  e  注：函数gx的图像如下， （2）因为 f xlnxaxxaR有两个不同的零点m,n， lnmamm 0 ammlnm 由题知0mn，且 ，即 ，  lnnann 0  annlnn lnmlnn 相减得到：a1 mn lnmlnn 因为k1a1(mkn)恒成立，即k1mkn 恒成立， mn {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}m k n m 所以k1 ln 恒成立． m n 1 n 设t m ，则t0,1时，不等式k1 tklnt 恒成立， n t1 t1 因为tk 0,t10进而得lntk1 0在t0,1时恒成立， tk t1 设htlntk1 ,t0,1， tk 1 tkt1 则ht k1 ， t tk2 1 k12 t2k2tk2t t1 tk2 即ht    ， t tk2 ttk2 ttk2 t1 又因为t0,1且k0，则 0，所以当k 1时，tk2 0， ttk2 即ht0，故ht在t0,1单调递增， 因为h10，所以ht0恒成立，故k 1满足题意． 当0k1时，若t  k2,1  ，由ht0，则ht在t  k2,1  单调递减， 所以当t  k2,1  时ht0，与题设不符． 综上所述，正数k的取值范围  k k 1  ． .........................................................10分 （3）令g(x)ex x1，则g(x)ex 1 当x0时，g(x)0，g(x)在(0,+)上单调递增； 当x0时，g(x)0，g(x)在(,0)上单调递减. 所以x0为g(x)极小值点，即最小值点，所以g(x) g(0)0 即ex  x1当且仅当x0时等号成立. t1lnt y lnxlny 2 由（2）知：0t1,2 ，进一步取t  0 y x，则  ； t1 x xy xy 1 1 1 不妨假设 p   x 1   x1 y1   x 2   x2 y2   x 3   x3 y3        y   y   y  1 2 3 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}1lnx lny lnx lny lnx lny  则lnP  1 1  2 2  3 3 2 x y x y x y  1 1 2 2 3 3 1 2 2 2  故lnP     2x y x y x y  1 1 2 2 3 3 1 1 1   1 1 1 进一步：Pex1 y1 x2 y2 x3 y3    1 x  y x  y x  y 1 1 2 2 3 3 1 1 1  1 1 1  另外：        x y x y x y   x y x y x y x y x y x y  1 1 2 2 3 3 1 1 2 2 3 3 1 1 2 2 3 3 1  x x x y y y  1 2 3 1 2 3  1 1 1  又 x y  x y  x y     x 1  y 1  x 2  y 2  x 3  y 3   1 1 2 2 3 3 x y x y x y x y x y x y 3 2 2  1 1  3 3  2 2  1 1  3 3 9， x y x y x y x y x y x y 1 1 2 2 2 2 3 3 3 3 1 1 当且仅当x  y  x  y  x  y 时等号成立 1 1 2 2 3 3 1  1  1 1 1 1 9 mn9 则Pex1 y1 x2 y2 x3 y3    11  . x y x y x y mn mn 1 1 2 2 3 3 1 1 1 即   x 1   x1 y1   x 2   x2 y2   x 3   x3 y3  mn9 ............................................................17分   y     y     y   m n 1 2 3 {#{QQABIQAs5wAQkIRACD56B02kCwiYsIETJCgGwUAWOAYKgYFAFKA=}#}