文档内容
石家庄市 2025 届普通高中学校毕业年级教学质量摸底检测
数学
(本试卷满分150分,考试时间120分钟)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在
本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.设集合 , ,则 ( )
A. B. C. D.
2.已知复数z满足 ,则复数z的虚部为( )
A. B. C. D.
3.已知平面向量a,b满足 ,且 , ,则向量a,b的夹角为( )
A. B. C. D.
4.已知正四棱锥底面边长为2,且其侧面积的和是底面积的2倍,则此正四棱锥的体积为( )
A. B. C. D.
5.已知 , ,则 ( )
A.3 B. C. D.
6.若数列 为等差数列, 为数列 的前n项和, , ,则 的最小值为(
)
A. B. C. D.7.已知双曲线 的左、右焦点分别为 、 ,过坐标原点的直线与双曲线C交于A、B两
点,若 ,则 ( )
A. B. C. D.4
8.已知函数 为定义在R上的奇函数,且在 上单调递减,满足
,则实数a的取值范围为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知实数a,b,c满足 ,则下列选项正确的是( )
A. B. C. D.
10.已知函数 ,则下列说法正确的是( )
A.当 时, 在 上单调递增
B.若 ,且 ,则函数 的最小正周期为
C.若 的图象向左平移 个单位长度后,得到的图象关于y轴对称,则 的最小值为3
D.若 在 上恰有4个零点,则 的取值范围为
11.如图,曲线C过坐标原点O,且C上的动点 满足到两个定点 , 的距
离之积为9,则下列结论正确的是( )A.
B.若直线 与曲线C只有一个交点,则实数k的取值范围为
C. 周长的最小值为12
D. 面积的最大值为
三、填空题:本题共3小题,每小题5分,共15分
12.在等比数列 中, , ,则 ____________.
13.已知函数 ,若 与 的图象相切于A、B两点,则直线
的方程为____________.
14.金字塔在埃及和美洲等地均有分布,现在的尼罗河下游,散布着约80座金字塔遗迹,大小不一,其中
最高大的是胡夫金字塔,如图,胡夫金字塔可以近似看做一个正四棱锥,则该正四棱锥的5个面所在的平
面将空间分成____________部分(用数字作答).
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
已知抛物线 的焦点为F,A是抛物线上横坐标为2且位于x轴上方的点,A到抛物线焦
点的距离为 .
(1)求抛物线C的方程;(2)若过点F的直线l交抛物线C于B、D两点(异于O点),连接 、 ,若 ,
求 的长.
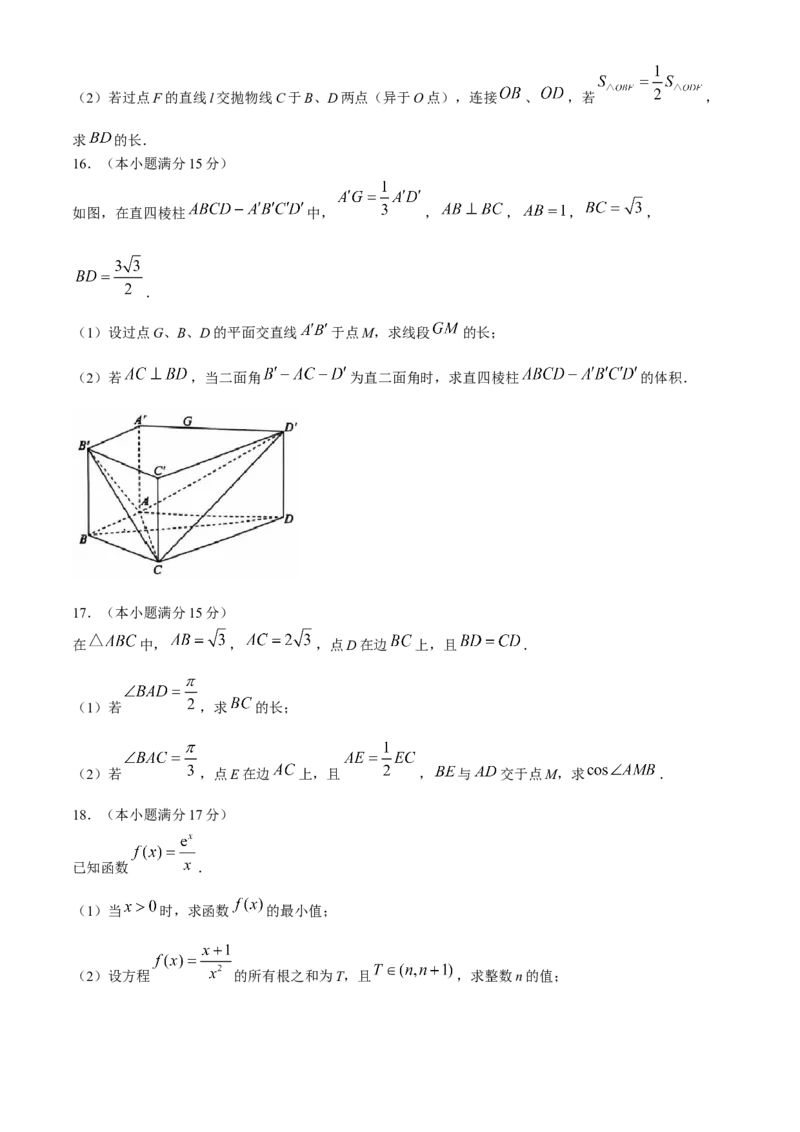
16.(本小题满分15分)
如图,在直四棱柱 中, , , , ,
.
(1)设过点G、B、D的平面交直线 于点M,求线段 的长;
(2)若 ,当二面角 为直二面角时,求直四棱柱 的体积.
17.(本小题满分15分)
在 中, , ,点D在边 上,且 .
(1)若 ,求 的长;
(2)若 ,点E在边 上,且 , 与 交于点M,求 .
18.(本小题满分17分)
已知函数 .
(1)当 时,求函数 的最小值;
(2)设方程 的所有根之和为T,且 ,求整数n的值;(3)若关于x的不等式 恒成立,求实数a的取值范围.
19.(本小题满分17分)
母函数(又称生成函数)就是一列用来展示一串数字的挂衣架.这是数学家赫伯特·维尔夫对母函数的一个
形象且精妙的比喻.
对于任意数列 ,即用如下方法与一个函数联系起来:
,则称 是数列 的生成函数.
例如:求方程 的非负整数解的个数.
设此方程的生成函数为 ,其中x的指数代表 的值.
,则非负整数解的个数为 .
若 ,则 ,可得 ,于是可得函数 的收缩
表达式为: .
故
(广义的二项式定理:两个数之和的任意实数次幂可以展开为类似项之和的恒等式)
则
根据以上材料,解决下述问题:
定义“规范01数列” 如下: 共有 项,其中m项为0,m项为1,且对任意 ,
,不同的“规范01数列”个数记为 .
(1)判断以下数列是否为“规范01数列”;
①0,1,0,1,0,1;②0,0,1,1,1,0,0,1;③0,1,0,0,0,1,1,1.
(2)规定 ,计算 , , , 的值,归纳数列 的递推公式;
(3)设数列 对应的生成函数为
①结合 与 之间的关系,推导 的收缩表达式;②求数列 的通项公式.
石家庄市 2025 届普通高中学校毕业年级教学质量摸底检测
数学答案
一、单选题:
1-5CABCD 6-8BAD
二、多选题:
9.BCD 10.ABD 11.AD
三、填空题:本题共3小题,每小题5分,共15分
12.16 13. 14.23
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.解:(1)由题意得 (2分)
解得 , (3分)
故抛物线方程为 . (5分)
(2)由题意得直线l的斜率不为0,设直线 ,与
联立得 ,由韦达定理得 , ① (7分)
设 , ,过O点做l垂线,垂足为G.
由 ,得 ,即
由 得 ② (9分)
由①②联立上式得 , , (11分)
. (13分)16.证明:(1)连接 ,由题意可得 , (2分)
又因为 平面 ,平面 平面 ,
平面 ,所以 ,由平行传递性可知 (4分)
所以M为靠近 的 三等分点, (6分)
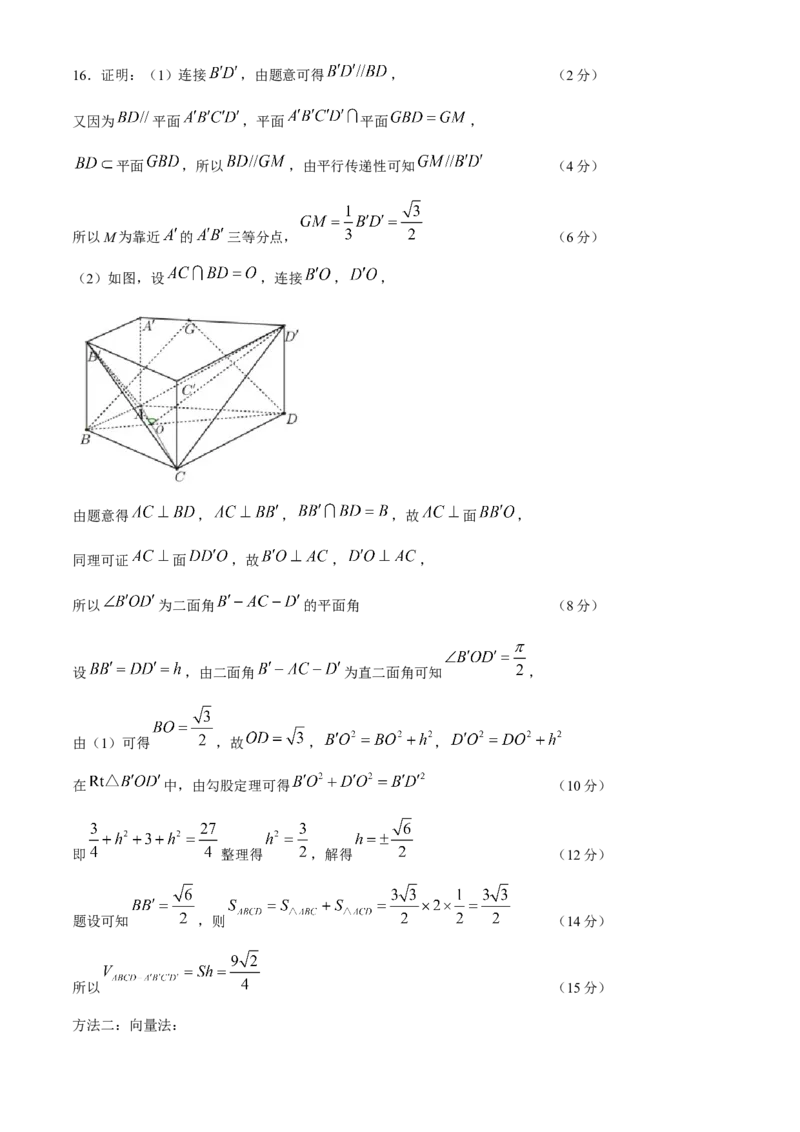
(2)如图,设 ,连接 , ,
由题意得 , , ,故 面 ,
同理可证 面 ,故 , ,
所以 为二面角 的平面角 (8分)
设 ,由二面角 为直二面角可知 ,
由(1)可得 ,故 , ,
在 中,由勾股定理可得 (10分)
即 整理得 ,解得 (12分)
题设可知 ,则 (14分)
所以 (15分)
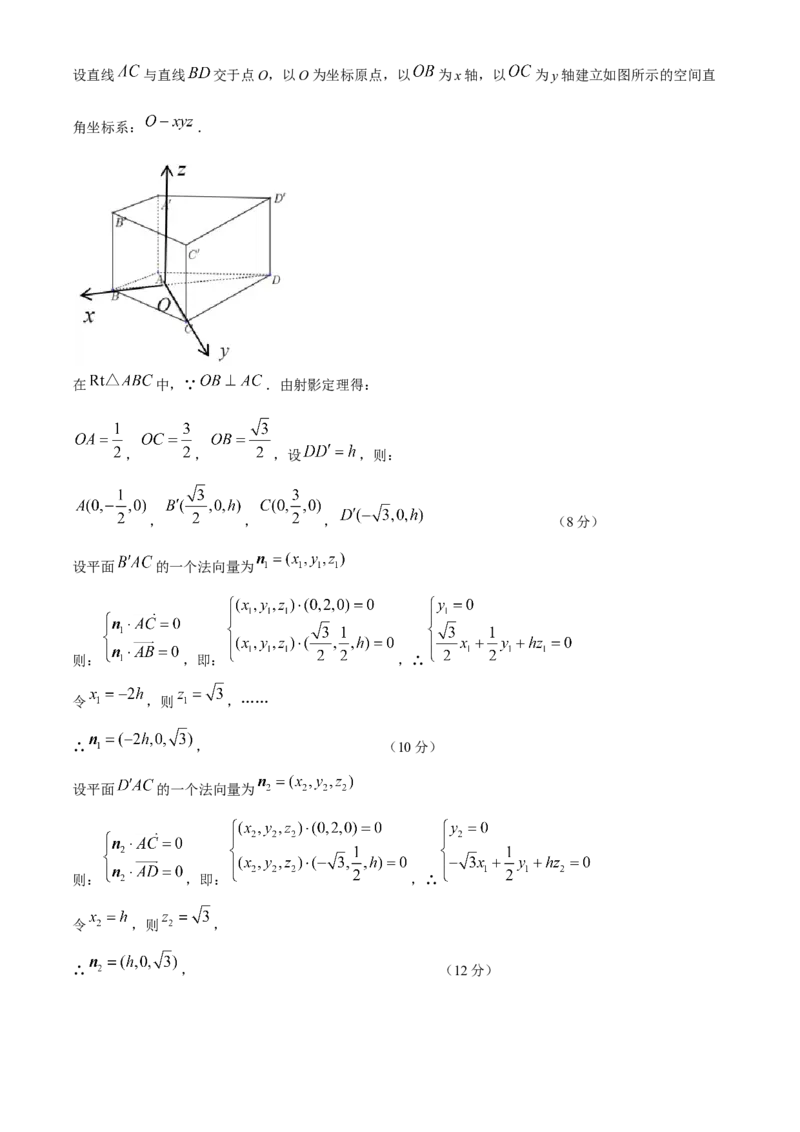
方法二:向量法:设直线 与直线 交于点O,以O为坐标原点,以 为x轴,以 为y轴建立如图所示的空间直
角坐标系: .
在 中,∵ .由射影定理得:
, , ,设 ,则:
, , , (8分)
设平面 的一个法向量为
则: ,即: ,∴
令 ,则 ,……
∴ , (10分)
设平面 的一个法向量为
则: ,即: ,∴
令 ,则 ,
∴ , (12分)当二面角 为直二面角时, ,即: ,得: . (13分)
∴ (15分)
17.解:(1)设
在 中, ① (2分)
在 中,由余弦定理
② (4分)
所以,
所以, , (6分)
(2) (7分)
(9分)
(11分)
(13分)
(15分)18.解:(1) , (2分)
, , 单调递减,
, , 单调递增, (3分)
; (4分)
(2)方程 可化简为
方程 的根就是函数 的零点,
易知 在 , 上单调递增 (5分)
因为 , ,
所以函数 在 有唯一零点 ,且 (7分)
因为 , ,
所以函数 在 有唯一零点 ,且 (9分)
则 ,因此, . (10分)
(3)设 ,则当 时 恒成立,
(12分)
①由(1)得 ,
当 时,, , 单调递减,
, , 单调递增,
∴ (14分)
②当 时, ,这与 矛盾, (16分)
综上, . (17分)
19.解析:
(1)由题意得①,③是“规范01数列”, (2分)
对于②,由于 时, ,故②不是“规范01数列”; (3分)
(2) , , , ; (每个1分)(7分)
“规范01数列” 中,首项 ,若 同时满足:
①当 时, ;②当 时, ,
此时可将 划分为两部分,即 和 ,由于 且 ,则
可构成一个“规范01数列”,所以数列 的递推公式为:
(9分)
(注:学生由 得出 也可给到10分)
(3)①
∴ (10分)
即由于
当 时, (舍去)
当 时, ,满足题意
故 的收缩表达式为 ; (12分)
②
(14分)
(15分)
故数列 的通项公式为 (17分)(注:其余方法得出 均可给到17分)