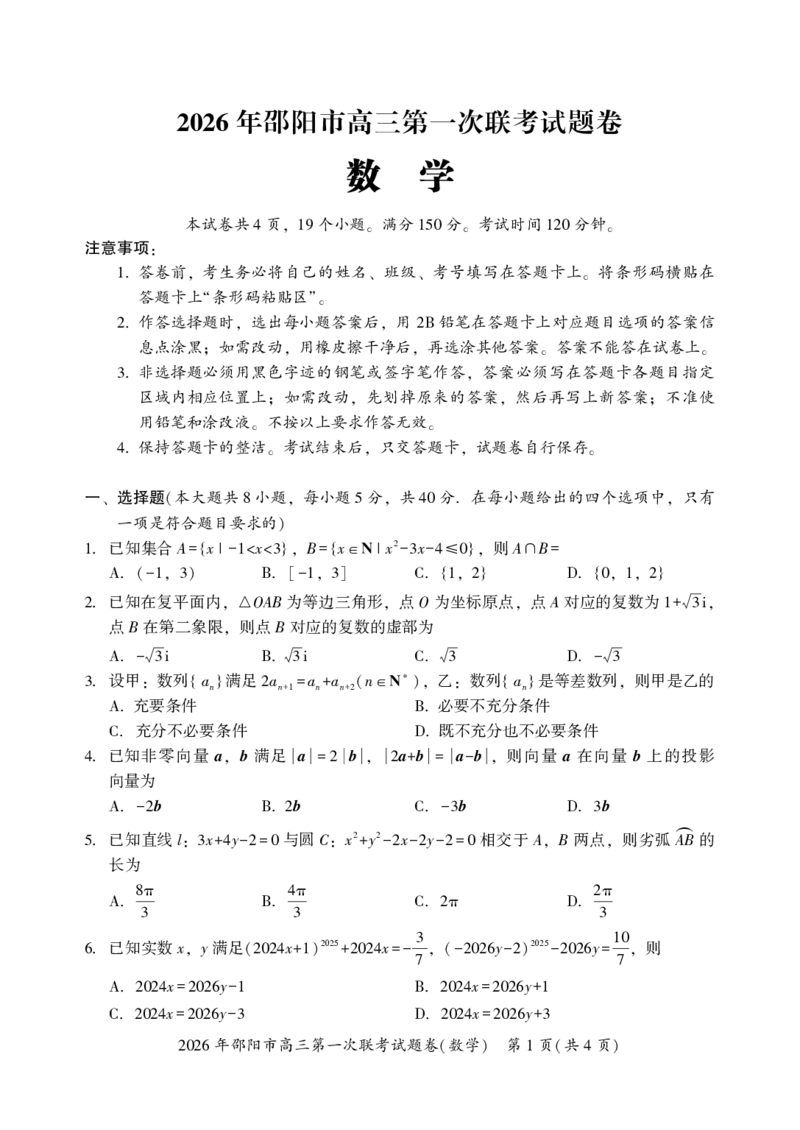文档内容
2026 年邵阳市高三第一次联考试题卷
数 学
本试卷共 页 个小题 满分 分 考试时间 分钟
4 , 19 。 150 。 120 。
注意事项
:
答卷前 考生务必将自己的姓名 班级 考号填写在答题卡上 将条形码横贴在
1. , 、 、 。
答题卡上 条形码粘贴区
“ ”。
作答选择题时 选出每小题答案后 用 铅笔在答题卡上对应题目选项的答案信
2. , , 2B
息点涂黑 如需改动 用橡皮擦干净后 再选涂其他答案 答案不能答在试卷上
; , , 。 。
非选择题必须用黑色字迹的钢笔或签字笔作答 答案必须写在答题卡各题目指定
3. ,
区域内相应位置上 如需改动 先划掉原来的答案 然后再写上新答案 不准使
; , , ;
用铅笔和涂改液 不按以上要求作答无效
。 。
保持答题卡的整洁 考试结束后 只交答题卡 试题卷自行保存
4. 。 , , 。
一 选择题 本大题共 小题 每小题 分 共 分 在每小题给出的四个选项中 只有
、 ( 8 , 5 , 40 . ,
一项是符合题目要求的
)
. 已知集合A {x x } B {x N x2 x } 则A B
1 = | -1< <3 , = ∈ | -3 -4≤0 , ∩ =
{ } { }
A. (-1, 3) B. [-1, 3] C. 1, 2 D. 0, 1, 2
. 已知在复平面内 OAB为等边三角形 点O为坐标原点 点A对应的复数为
2 , △ , , 1+ 3i,
点B在第二象限 则点B对应的复数的虚部为
,
A. - 3i B. 3i C. 3 D. - 3
. 设甲 数列{ a }满足 a a a n N
3 : n 2 n +1= n+ n +2( ∈
年邵阳市高三第一次联考试题卷 数学 第 页 共 页
2026 ( ) 1 ( 4 )
∗ 乙 数列{ a }是等差数列 则甲是乙的
), : n ,
充要条件 必要不充分条件
A. B.
充分不必要条件 既不充分也不必要条件
C. D.
. 已知非零向量 a b 满足 a b a b a b 则向量 a 在向量 b 上的投影
4 , =2 , 2 + = - ,
向量为
b b b b
A. -2 B. 2 C. -3 D. 3
. 已知直线l x y 与圆C x2 y2 x y 相交于 A B 两点 则劣弧 AB
5 : 3 +4 -2=0 : + -2 -2 -2=0 , ,
(
的
长为
8π 4π 2π
A. B. C. 2π D.
3 3 3
. 已知实数x y满足 x 2025 x 3 y 2025 y 10 则
6 , (2024 +1) +2024 =- , (-2026 -2) -2026 = ,
7 7
x y x y
A. 2024 =2026 -1 B. 2024 =2026 +1
x y x y
C. 2024 =2026 -3 D. 2024 =2026 +3b a
. 已知随机变量X N 正实数a b 满足P x a P x b 则 +3的
7 ~ (2, 3), , ( ≤3 +2)= ( ≥4 -1), a+ b
4
最小值为
A. 3 B. 4 C. 5 D. 6
. 设函数f x x 2和g x x 2 的零点分别为x x 其中a . 当a 时
8 ( )= -ax ( )= - x 1, 2, >1 ∈[2, +∞) ,
loga
则x x 的取值范围为
1+32 2
A. [16 2, +∞) B. [16, +∞) C. [65, +∞) D. [65 2, +∞)
二 选择题 本大题共 小题 每小题 分 共 分. 在每小题给出的选项中 有多项符
、 ( 3 , 6 , 18 ,
合题目要求. 全部选对的得 分 部分选对的得部分分 有选错的得 分
6 , , 0 )
x2 y2
. 已知双曲线E a b 的离心率为 7 左 右焦点分别为 F
9 : a2 -b2 =1( >0, >0) , 、 1(- 7, 0),
2
F 过F 的直线与E的右支相交于P Q两点 则下列结论错误的是
2( 7, 0), 2 , ,
x2 y2 ∙∙
E的方程为
A. - =1
4 3
PQ
B. ≤3
E的渐近线方程为x y
C. ± 3 =0
当 F F OP 时 PF F 的面积为
D. 1 2 =2 , △ 1 2 3
( )
. 已知函数f x A wx φ w φ π 的部分图象如图 一 所示 则下列说法
10 ( )= sin( + ) >0, < ( ) ,
2
正确的是
( )
f x x π
A. ( )= 2sin 2 -
3
( )
若f α 2 则 α π 7
B. ( )= , sin 4 - =
3 6 9
把函数 y f x 的图象向左平移π个单位后得到函数
C. = ( )
6
y g x 的图象 则y g x 为偶函数
= ( ) , = ( )
若函数 f x 的导函数为 h x 则 h x 的图象关于
D. ( ) ( ), ( )
( ) 图 一
点 5π 对称 ( )
, 0
12
. 已知圆台O O 的上 下底面的面积分别为 和 则下列结论正确的是
11 1 2 、 9π 16π,
若圆台O O 存在内切球 则内切球的体积为
A. 1 2 , 32 3π
若圆台O O 的母线与下底面所成的角为 则圆台O O 的外接球的表面积为56π
B. 1 2 60°, 1 2
3
若圆台O O 的外接球的体积为500π 则圆台O O 的表面积为
C. 1 2 , 1 2 25π+35 2π
3
若圆台O O 的外接球的体积为500π 则圆台O O 的体积为259π或37π
D. 1 2 , 1 2
3 3 3
年邵阳市高三第一次联考试题卷 数学 第 页 共 页
2026 ( ) 2 ( 4 )三 填空题 本大题共 小题 每小题 分 共 分
、 ( 3 , 5 , 15 )
. 设等比数列{ a }的前n项和为S 若a a 则S .
12 n n, 1=2, 4=16, 4=
. 已知多项式 ax x 5 a a x a x2 a x3 a x4 a x5 a x6 若 a a a
13 ( -2)(1+ ) = 0+ 1 + 2 + 3 + 4 + 5 + 6 , 1+ 3+ 5=16,
则a .
=
. 已知正四面体ABCD 的棱长为 用满足 MA2 MB2 MC2 MD2 的动点 M 构成的平
14 4 2, + = +
面截正四面体ABCD 则所得截面的面积为 .
,
四 解答题 本大题共 小题 共 分. 解答应写出文字说明 证明过程或演算步骤
、 ( 5 , 77 、 )
. 分 在 ABC中 内角A B C的对边分别为a b c.已知 2B A B C 2C .
15 (13 ) △ , , , , , sin +3sin cos sin -2sin =0
若a c 求 ABC的外接圆的半径
(1) = 2, =2, △ ;
若 A 2 b 求 ABC的面积.
(2) cos = , =2, △
3
. 分 如图 二 在四棱锥 P ABCD 中 底面 ABCD 为直角梯形 AB AD
16 (15 ) ( ), - , , ⊥ ,
AD BC AD AP AB BC PA 平面ABC E为棱PD上的点.
∥ , = =2, = =1, ⊥ ,
当E为棱PD的中点时 证明 EC 平面PAB
(1) , : ∥ ;
在棱PD上是否存在点E 使得平面PAC与平面 EAC 的夹角的余弦值为 3 若存
(2) , ?
3
在 请确定点E的位置 若不存在 请说明理由.
, ; ,
图 二
( )
年邵阳市高三第一次联考试题卷 数学 第 页 共 页
2026 ( ) 3 ( 4 ). 分 国家近年来对机器人的研究 尤其是在人形机器人和具身智能领域方面 出
17 (15 ) , ,
台了一系列的政策 旨在推动技术创新 产业升级和规模化应用. 某学校为响应国家
, 、
号召 培养学生的创新能力 举办机器人比赛 经过初赛 甲班团队和乙班团队进入
, , , ,
了决赛阶段. 决赛阶段规定 对每一轮比赛 获胜方记 分 另一方记 分 无平
: , 1 , 0 ,
局 当两团队累积得分的分差为 分时 比赛结束 累积得分高的团队获冠军. 若每
; 3 , ,
轮比赛中 甲班团队获胜的概率为2 且每轮比赛的结果相互独立.
, ,
3
若比赛结束时恰好进行了 轮比赛 求甲班团队获得冠军的概率
(1) 3 , ;
若比赛最多进行 轮 求比赛结束时比赛轮数X的分布列及数学期望E X
(2)(ⅰ) 5 , ( );
若比赛轮数不限制 求甲班团队获得冠军的概率.
(ⅱ) ,
x2 y2
. 分 已知椭圆E a b 的左 右焦点分别为 F F 离心率 e 1
18 (17 ) : a2 +b2 =1( > >0) 、 1, 2, = ,
2
过F 的直线l交E于A B两点 ABF 的周长为 .
2 , , △ 1 8
求E的方程
(1) ;
过点F 且与l垂直的直线与E相交于C D两点 A C 在 x 轴的上方 M N 分
(2) 2 , , , , ,
别为线段AB 线段CD的中点 直线AC与直线BD相交于点R.
, ,
直线 MN 是否过定点 若过定点 请求出定点坐标 若不过定点 请说明
(ⅰ) ? , ; ,
理由
;
求 MNR的面积的最小值.
(ⅱ) △
. 分 若函数f x g x 对任意 x D 总存在唯一的 x D 使 f x g x k
19 (17 ) ( ), ( ) 1∈ , 2∈ , ( 1)+ ( 2)=
成立 则称f x 是 g x 在区间 D 上的 k 阶和函数 . 特别地 当 f x g x 时
, ( ) ( ) “ ” , ( )= ( ) ,
称f x 为区间D上的 k阶自和函数 .
( ) “ ”
判断函数f x x 是否为区间 上的 阶自和函数
(1) ( )=log3( +1) [2, 26] “3 ”;
若函数f x 4 是 g x x2 ax a2 在区间 上的 阶和函数
(2) ( )= x ( )= -2 + -1 [0, 2] “2 ”,
+2
求实数a的取值范围
;
若函数f x x 为区间 a a 上的 阶自和函数 当 b 时 函数
(3) ( )= 2 [ , +1] “2 ”, >1 ,
φ x x a x b x2 x 有两个零点x x 证明 x x 1.
( )=( - -log23)ln +( -1)( -2 ) 1, 2, : 2< 1+ 2<3-b
年邵阳市高三第一次联考试题卷 数学 第 页 共 页
2026 ( ) 4 ( 4 )