数学答案-2026届高三扬州一模(1)_2026年1月_260122江苏省扬州市2026届高三上学期期末考试(扬州一模)（全科）

江苏省扬州市2026届高三上学期期末考试 数学试题 一、单选题：本题共 8 小题，每小题 5分，共 40 分，每小题只有一个选项符合要求 1.设 A=  xZ∣x2 9  ,B=0,1,2,3 ,则集合 AB 中元素的个数为 A. 3 B. 4 C. 5 D. 6 【答案】D 【解析】A=−2,−1,0,1,2,AB=−2,−1,0,1,2,3 ,共 6 个元素. 2.已知复数 z 满足 (1−i)z =1+i ，则 z 等于 A. 1 B. 2 C. 2 D. 3 【答案】A 【解析】1−i z = 1+i , 2 z = 2, z =1. 3.若 P(x ,4) 为抛物线 y2 =4x 上一点,则点 P 到其焦点的距离为 0 A. 4 B. 5 C. 2 5 D. 6 【答案】B 【解析】P(x ,4) 在抛物线 y2 =4x 上， 16=4x ， x =4 ， P 到焦点的距离 4+1=5. 0 0 0 2x −a,x0,  4.已知函数 f (x)= 1 x 为奇函数,则 a+b 的值为 b−   ,x0.  2 A. 0 B. -2 C. 2 D. 1 【答案】C 【解析】 f (x) 为奇函数,则 f (0)=0,20 −a=0,a=1 f (−1)+ f (1)=0,b−2+2−a=0,b=a=1,a+b=2. 5.已知第一组数据 x ,x ,x , ,x 的平均数为 x ,方差为 s2 ,第二组数据 x ,x ,x , ,x ,x 的平均数为 x , 1 2 3 n 1 2 3 n 方差为 s'2 ,则 A. B. C. D. x= x,s2 s'2 x= x,s2 s'2 x x,s2 s'2 x x,s2 s'2 【答案】A 【解析】一组数据加上平均数后, 平均数不变, 方差变小. 学科网（北京）股份有限公司  6.函数 y=sin  2x−  −cosx 在区间 0,2 上的零点个数为  3 A. 3 B. 4 C. 5 D. 6 【答案】B   【解析】画作 y=sin  2x−  与 y =cosx 的图象,两个函数共有 4 个交点.  3 7.在无穷正项等差数列 a  中,记 S 为数列 a  的前 n 项和,则 “ a =3a +2 ” 是 “数列 n n n 2 1 学科网（北京）股份有限公司  S n + n  是等差数列” 的 A. 充分且不必要条件 B. 必要且不充分条件 C. 充要条件 D. 既不充分又不必要条件 【答案】C 【解析】当 a =3a +2 时,则 2 1 a +d =3a +2,d =2a +2 1 1 1 n(n−1) n(n−1) S =na + d =na + (2a +2)=na +n(n−1)(a +1)=n2a +n2 −n n 1 2 1 2 1 1 1 1   S +n=n2a +n2 =n2(a +1),  S +n = a +1n,  S +n  是等差数列,充分; 当 S n +n 是等差 n 1 1 n 1 n 数列时, S +n = An+B , n S =(An+B)2 = A2n2 +2ABn+B2 −n,S  是等差数列的前 n 项和 n n n(n−1) d  d  B2 =0,S = A2n2 −n ,而 S =na + d = n2 +  a −  n , n n 1 2 2  1 2 d a − =−1,d =2a +2,a =3a +2 ,必要. 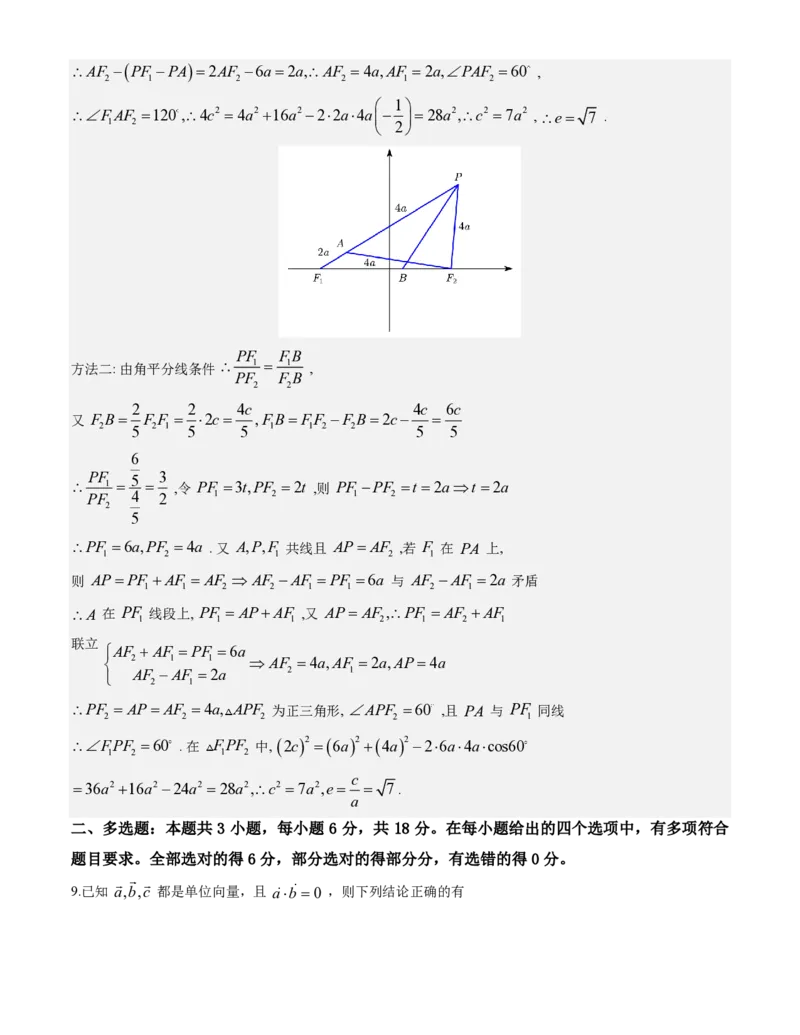1 2 1 2 1 8.已知双曲线的左、右焦点为 F 、 F ,P 为双曲线的右支上一点,直线 PF 与左支交于点 A ,且 1 2 1 2 AP= AF .FPF 的平分线与 x 轴交于点 B,F B= F F ,则双曲线 C 的离心率为 2 1 2 2 5 2 1 A. 2 B. 3 C. 5 D. 7 【答案】D PF BF 3 【解析】方法一: PB 为 FPF 角平分线,  1 = 1 = , 1 2 PF BF 2 2 2 PF −PF =2a,PF =6a,PF =4a,AF −AF =2a , 1 2 1 2 2 1AF −(PF −PA)=2AF −6a=2a,AF =4a,AF =2a,PAF =60 , 2 1 2 2 1 2  1 FAF =120,4c2 =4a2 +16a2 −22a4a  −  =28a2,c2 =7a2 , e= 7 . 1 2  2 PF FB 方法二: 由角平分线条件  1 = 1 , PF F B 2 2 2 2 4c 4c 6c 又 F B= F F = 2c= ,FB=FF −F B=2c− = 2 5 2 1 5 5 1 1 2 2 5 5 6 PF 5 3  1 = = ,令 PF =3t,PF =2t ,则 PF −PF =t =2at =2a PF 4 2 1 2 1 2 2 5 PF =6a,PF =4a . 又 A,P,F 共线且 AP= AF ,若 F 在 PA 上, 1 2 1 2 1 则 AP=PF +AF = AF  AF −AF =PF =6a 与 AF −AF =2a 矛盾 1 1 2 2 1 1 2 1 A 在 PF 线段上, PF = AP+AF ,又 AP= AF ,PF = AF +AF 1 1 1 2 1 2 1 联立 AF + AF = PF =6a  2 1 1  AF =4a,AF =2a,AP=4a AF −AF =2a 2 1  2 1 PF = AP= AF =4a,APF 为正三角形, APF =60 ,且 PA 与 PF 同线 2 2 2 2 1 FPF =60 . 在 FPF 中, (2c)2 =(6a)2 +(4a)2 −26a4acos60 1 2 1 2 c =36a2 +16a2 −24a2 =28a2,c2 =7a2,e= = 7. a 二、多选题：本题共 3 小题，每小题 6 分，共 18 分。在每小题给出的四个选项中，有多项符合 题目要求。全部选对的得 6分，部分选对的得部分分，有选错的得 0分。     9.已知 a,b,c 都是单位向量，且 ab =0 ，则下列结论正确的有 学科网（北京）股份有限公司(  )  ( )   A. a+b  a−b =0 B. a+b = a−b       3 4  C. b 与 a−b 的夹角为 D. 存在 c ,使得 c = a+ b 4 5 5 【答案】ABD  ( )( ) 【解析】 a+b a−b =a2 −b2 =1−1=0 , A 对.  2 2 a+b =a2 +2ab+b2 =2, a−b =a2 −2ab+b2 =2,a+b = a−b ,B 对.    (      ) −1 2 与 a−b 夹角为 b a−b =−1,cosb,a−b = =− ,b 1 2 2 3  9 24  16 9 16 c2 = a2 + ab+ b2 = + =1 , D 对. 4 25 25 25 25 25 10.已知直线 l:(x−1)cos+ ysin−2=0 与圆 C:(x−2)2 +(y−1)2 =16 相交于 A,B 两点,则下列结论正 确的有 A. 直线 l 过一定点 B. 直线 l 与圆 x2 + y2 −2x−3=0 相切 C. 点 C 到 l 的最大距离为 2+ 2 D. ABC 的面积恒小于 8 【答案】BC 【解析】直线 l 不可能过定点, A 错. 圆 x2 + y2 −2x−3=0 ,圆心 (1,0) ,半径 2,直线 l:xcos+ ysin−cos−2=0 直线 l 与 x2 + y2 −2x−3=0 相切, B 对. cos−cos−2 d = =2=r, cos2+sin2 2cos+sin−cos−2   C(2,1) 到直线 l 距离 d = = cos+sin−2 = 2sin  +  −2  2+2,C 1 1  4 对. S = 1 2 16−d2d = −d4 +16d2 = − ( d2 −8 )2 +64,d2 =8 即 d =2 2 时, (S ) =8 ，D ABC 2 1 1 1 1 1 1 1 ABC max 错. 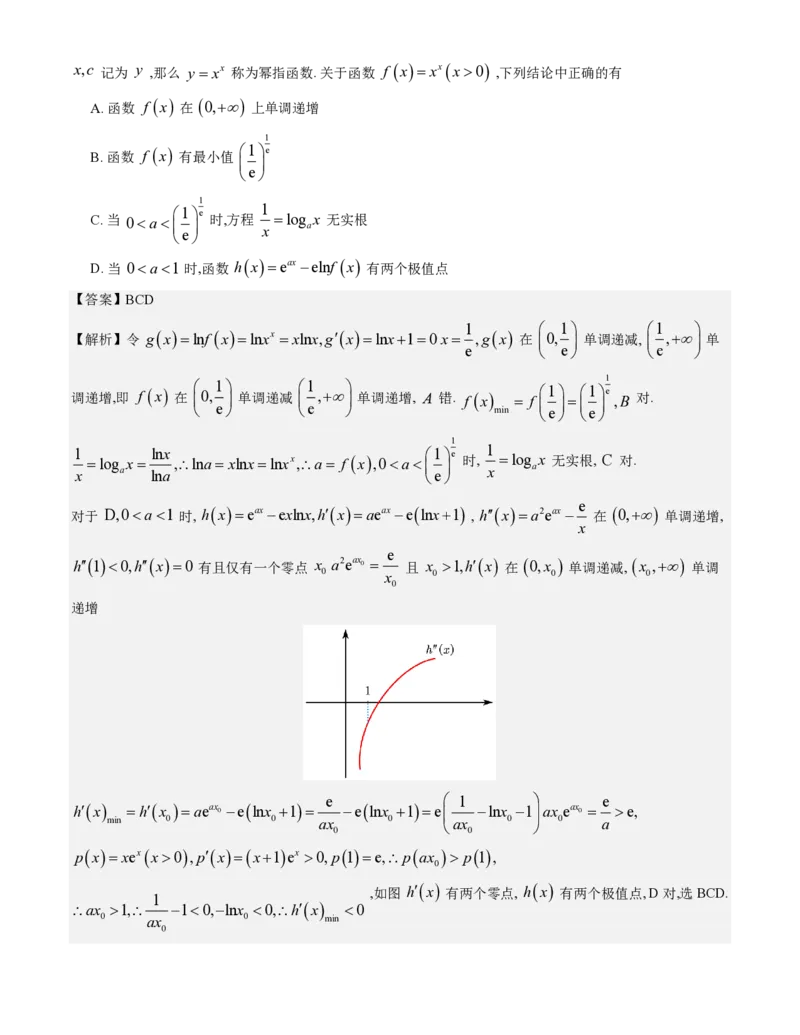11.对于等式 ab =c ,如果将 a 视为自变量 x,b 视为常数, c 记为 y ,那么 y = xb 为幂函数; 如果将 a(a0,a1) 视为常数, b 视为自变量 x,c 记为 y ,那么 y =ax 为指数函数; 如果将 a 、 b 视为自变量 学科网（北京）股份有限公司x,c 记为 y ,那么 y = xx 称为幂指函数. 关于函数 f (x)= xx(x0) ,下列结论中正确的有 A. 函数 f (x) 在 (0,+) 上单调递增 1 B. 函数 f (x) 有最小值 1e   e 1 C. 当 0a 1e 时,方程 1 =log x 无实根   x a e D. 当 0a1 时,函数 h(x)=eax −elnf (x) 有两个极值点 【答案】BCD 1  1 1  【解析】令 g(x)=lnf (x)=lnxx = xlnx,g(x)=lnx+1=0 x= ,g(x) 在  0,  单调递减,  ,+  单 e  e e  1 调递增,即 f (x) 在   0, 1  单调递减   1 ,+   单调递增, A 错. f (x) = f 1 = 1e ,B 对.  e e  min  e    e   1 1 =log x= lnx ,lna= xlnx=lnxx,a= f (x),0a 1e 时, 1 =log x 无实根, C 对. 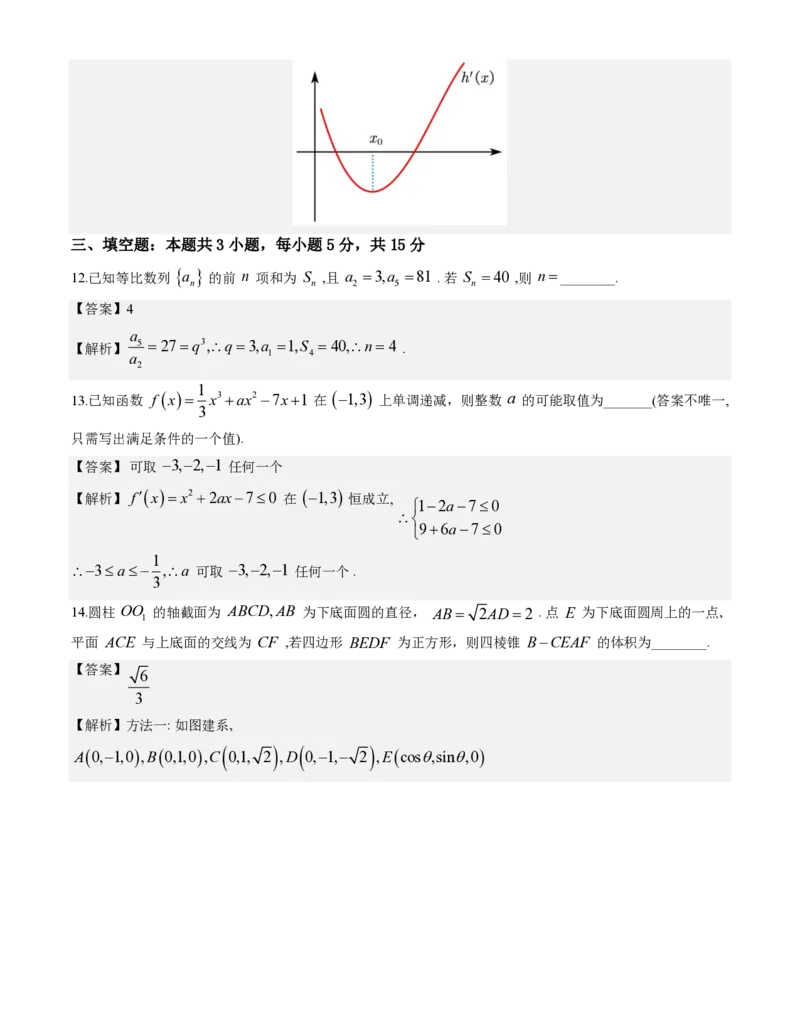x a lna  e   x a e 对于 D,0a1 时, h(x)=eax −exlnx,h(x)=aeax −e(lnx+1) , h(x)=a2eax − 在 (0,+) 单调递增, x e h(1)0,h(x)=0 有且仅有一个零点 x a2eax 0 = 且 x 1,h(x) 在 (0,x ) 单调递减, (x ,+) 单调 0 x 0 0 0 0 递增 e  1  e h(x) =h(x )=aeax 0 −e(lnx +1)= −e(lnx +1)=e −lnx −1ax eax 0 = e, min 0 0 ax 0 ax 0 0 a   0 0 p(x)= xex(x0),p(x)=(x+1)ex 0,p(1)=e,p(ax ) p(1), 0 ,如图 h(x) 有两个零点, h(x) 有两个极值点, D 对,选 BCD. 1 ax 1, −10,−lnx 0,h(x) 0 0 ax 0 min 0 学科网（北京）股份有限公司三、填空题：本题共 3 小题，每小题 5分，共 15 分 12.已知等比数列 a  的前 n 项和为 S ,且 a =3,a =81 . 若 S =40 ,则 n=________. n n 2 5 n 【答案】4 a 【解析】 5 =27=q3,q=3,a =1,S =40,n=4 . a 1 4 2 1 13.已知函数 f (x)= x3+ax2 −7x+1 在 (−1,3) 上单调递减，则整数 a 的可能取值为_______(答案不唯一, 3 只需写出满足条件的一个值). 【答案】 可取 −3,−2,−1 任何一个 【解析】 f(x)= x2 +2ax−70 在 (−1,3) 恒成立, 1−2a−70  9+6a−70 1 −3a− ,a 可取 −3,−2,−1 任何一个 . 3 14.圆柱 OO 的轴截面为 ABCD,AB 为下底面圆的直径， AB= 2AD=2 . 点 E 为下底面圆周上的一点, 1 平面 ACE 与上底面的交线为 CF ,若四边形 BEDF 为正方形，则四棱锥 B−CEAF 的体积为________. 【答案】 6 3 【解析】方法一: 如图建系, ( ) ( ) A(0,−1,0),B(0,1,0),C 0,1, 2 ,D 0,−1,− 2 ,E(cos,sin,0) 学科网（北京）股份有限公司设平面 ACE 的法向量     nAE =0 xcos+(sin+1)y =0 n =(x,y,z),  , nAC =0 2y+ 2z =0 不妨设 y=cos ,则 x=−sin−1,z =− 2cos ,   ( ) ( ) n = −sin−1,cos,− 2sin ,F x ,y , 2 ,CF =(x ,y −1,0),CFn =0 0 0 0 0 x (−sin−1)+cos(y −1)=0 ① 0 0  BEDF 为正方形, BE =(cos,sin−1,0),FD=(−x ,−1−y ,0) , 0 0 ,  cos=−x ,?② ( ) BF = x ,y −1, 2 , 0 ,BEBF =0 0 0 sin−1=−1− y ,?③  0 x cos+(y −1)(sin−1)=0 ,④ 0 0 cos2+(sin−1)2 = x2 +(y −1)2 +2 ⑤, 0 由①②③④⑤解得  1 sin=  2  1  y =   0 2  3  cos=  2  3  x =−  0 2  3 1   3 1  3 3   3 1  E ,− ,0,F− , , 2,CE = ,− ,− 2,AE = , ,0,         2 2 2 2 2 2 2 2         学科网（北京）股份有限公司33 FA= ,− ,− 2,AECE =0,CE = FA,CEAF 为矩形,   2 2     1 3 3 S = 5,n =− , ,− ,B 到平面 ACE 距离 CEAF  2 2 2      BAn 3 2 3 1 2 3 6 d =  = = V =  5 = . n 10 10 3 10 3 2 方法二: AB=2,AD= 2 ,设 AE = x,BE = 4−x2,DE = 2+x2  四边形 BEDF 为正方形, BE = DE 4−x2 = 2+x2  x=1 , 1 1 6 AE =1,BE = 3,V =2V =2V =2   3 2 = . B−CEAF B−AEC C−ABE 3 2 3 四、解答题：本题共 5 小题，共 77分，解答应写出文字说明，证明过程或演算步骤 2 7 15.记 ABC 内角 A 、 B 、 C 的对边分别为 a,b,c ,已知 a2 +c2 −b2 =− ac,sinA= sinB. 7 8 (1) 求 A ； 3 ( 2 )若 asinC = 3 ，求 AB 边上的高 . 2 a2 +c2 −b2 1 4 3 【解析】(1) cosB= =− ,sinB= 2ac 7 7 7 4 3 3  sinA=  = ,A= . 8 7 2 3 3  1 1 4 3 3 3 3 3 14 (2) sinC =sin(A+B)=   −  +  = ,a=  =7 2  7 2 7 14 2 3 3 4 3 AB 边上的高 h=asinB=7 =4 3 . 7 学科网（北京）股份有限公司16.在平面直角坐标系中，已知 F (−1,0),F (1,0) ，平面内一动点 P 满足 PF , FF , PF 成等差数列,记 1 2 1 1 2 2 点 P 的轨迹为曲线 C . (1)求曲线 C 的方程； (2)过点 M (0,−2) 的直线 l 交曲线 C 于 A,B 两点. ①若点 A 的坐标为 (2,0) ，求线段 AB 的长； ②若 OMA 的面积是 OMB 面积的 3 倍，求直线 l 的方程. ( ) 【解析】(1)  PF , FF , PF 成等差数列，  PF + PF =2 FF =4 4 FF 1 1 2 2 1 2 1 2 1 2 P 的轨迹为椭圆且 2a=4,a=2,c=1,b= 3 x2 y2  曲线 C 的方程为 + =1 . 4 3 (2)① 当 A(2,0) 时， k =k =1 ，直线 l 方程为 y = x−2 l MA y= x−2 2  (7x−2)(x−2)=0,x = , 3x2 +4y2 =12 B 7  2 12 2  AB = 1+1 x −x = 2  2−  = . A B  7 7 S MA ②  OMA = =3 ，设 A(x ,y ),B(x ,y ) ， x =3x ① S MB 1 1 2 2 1 2 OMB 设直线 l 方程为 y=kx−2 y=kx−2   ( 3+4k2) x2 −16kx+4=0,Δ0 3x2 +4y2 =12 且 由 ,代入③  16k  12k x +x = x =   1 2 3+4k2   1 3+4k2  ①②  4 4k   x x = x =  1 2 3+4k2  2 3+4k2 48k2 4 6  = k = ( 3+4k2)2 3+4k2 4 6  直线 l 的方程为 y= x−2 . 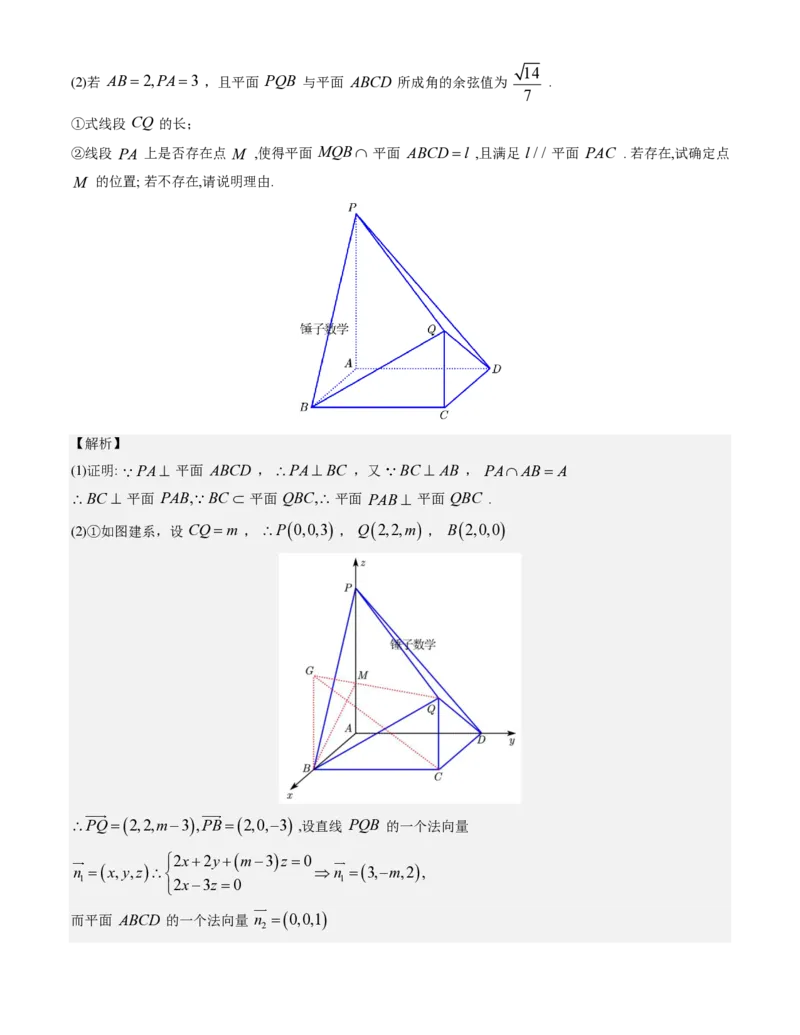4 17.如图，已知多面体 PQABCD 中， PA⊥ 平面 ABCD ， PA//QC ，底面 ABCD 为正方形. (1)求证:平面 PAB⊥ 平面 QBC ； 学科网（北京）股份有限公司14 (2)若 AB=2,PA=3 ，且平面 PQB 与平面 ABCD 所成角的余弦值为 . 7 ①式线段 CQ 的长； ②线段 PA 上是否存在点 M ,使得平面 MQB 平面 ABCD=l ,且满足 l// 平面 PAC . 若存在,试确定点 M 的位置; 若不存在,请说明理由. 【解析】 (1)证明:  PA⊥ 平面 ABCD ， PA⊥ BC ，又  BC ⊥ AB ， PAAB= A BC ⊥ 平面 PAB, BC  平面 QBC, 平面 PAB⊥ 平面 QBC . (2)①如图建系，设 CQ=m ， P(0,0,3) ， Q(2,2,m) ， B(2,0,0)  PQ=(2,2,m−3),PB=(2,0,−3) ,设直线 PQB 的一个法向量  2x+2y+(m−3)z =0 n =(x,y,z) n =(3,−m,2), 1 2x−3z =0 1  而平面 ABCD 的一个法向量 n =(0,0,1) 2 学科网（北京）股份有限公司 n n 2 14 1 2  = = m=1,CQ=1 . n n 13+m2 1 7 1 2 1 ② 设 MA=PA ，当 0 时，由 MA=3 ，延长 QM,CA 延长线于点 G 3 6 2  6 6  AG= ,l = BG ,此时 G  , ,0  , 1−3 3−1 3−1    2 6  若 l// 平面 PAC BG//AC ,而 BG=  , ,0  3−1 3−1   2 6 1 AC =(2,2,0) ,此时 = = ,舍去 3−1 3−1 3 1 当 1 时,仿上,也舍 3 1 1 当 = 时,交线 l//AC,l// 平面 PAC 符合, = 3 3 MA=1,M 为 PA 上靠近 A 的三等分点 . 18.某地文旅部门为了解天气状况对某景点旅游满意度的影响，分别于晴天和阴雨天在该景点调查了 200 位游 客，调查结果如下表. 满意 不满意 合计 晴天 80 阴雨天 40 合计 140 200 (1)完善上述表格，并判断能否有99%的把握认为当天天气状况对该景点旅游满意度有影响; (2)从这 200 位游客中任选两人，在两人调查当天的天气状况一致的条件下，试求他们对该景点均满意的概率； (3)当地天气多变，文旅部门根据以往数据，为游客发布如下天气信息:若第1天为晴天,则第 2 天为晴天的概率 2 1 2 1 为 ,为阴雨天的概率为 ; 若第 1 天为阴雨天,则第 2 天为阴雨天的概率为 ,为晴天的概率为 . 已知第 3 3 3 3 1 天是晴天, 求第 n 天仍是晴天的概率 P ,并求前 n 天晴天的天数 X 的期望 E(X) . n n(ad −bc)2 附录: 2 = ,n=a+b+c+d . (a+b)(c+d)(a+c)(b+d)  0.010 0.005 0.001 x 6.635 7.879 10.828  学科网（北京）股份有限公司【解析】(1)2×2 列联表如下: 满意 不满意 合计 晴天 80 20 100 阴雨天 60 40 100 合计 140 60 200 200(8040−2060)2 2 = 9.5246.635 10010014060  有 99% 的把握认为当天天气状况对该景点旅游满意度有影响. (2)记事件 A 为两个调查当天的天气状况一致，事件 B 为他们对该景点均满意 n(AB) C2 +C2 493 P(B∣A)= = 80 60 = n(A) C2 +C2 990 100 100 2 1 1 1 (3)由题意知 p = P + (1−P )= P + n+1 3 n 3 n 3 n 3 1 1 1 1 1 P − =  P −  ,P =1,P − = 0 n+1 2 3 n 2 1 1 2 2  1 1 1 P −  成首项为 ,公比为 的等比数列  n 2 2 3 n−1 n−1 1 11 1 1 1 P − = P = +      n 2 23 n 2 2 3 某一天要么是晴天,要么是雨天,它符合两点分布 1,?第 i 天为晴天 记第 i 天为  ，且  ={ i i 0,?第 i 天为雨天 1 1 n 1−    E(X)= E    n    = n E()= n P = n + 2 3  = n + 3 1−   1  n  .  i=1 i  i=1 i i=1 i 2 1− 1 2 4 3  3 19.已知函数 f (x)=ax+lnx ,直线 2x−y−1=0 与曲线 y = f (x) 相切. (1)求 a 的值； 1  (2)若对任意 x  ,e2  ，存在 c−e,0 ，使得不等式 (x+1) f (x) x2 +bx+c 成立,求 b 的最大值; e  (3)若 =exf (x) ，求证:对任意 s,t(1,+) ，有 (s+t)(s)+(t) . 【解析】(1)设切点为 学科网（北京）股份有限公司 1 1 1  a+ =2 x =1 (x ,ax +lnx ), f(x)=a+ ,k =a+  x  0 ,a=1 0 0 0 x x 0  2x − 0 ax −lnx −1=0 a=1  0 0 0 1  (2)对 x ,e2 ,c−e,0 使 (x+1)(x+lnx) x2 +bx+c   e  先处理 3,固定住 x, c−e,0 使之成立,即 xlnx+x+lnxbx+c 成立  只需 xlnx+x+lnxbx−e 即可! 1  再处理  ,即 xlnx+x+lnxbx−e 对 x ,e2 恒成立   e  xlnx+x+lnx+e (x+1)lnx+x+e (x+1)lnx+x+e b = ,b  x x x   min (x+1)lnx+x+e 令 g(x)= , x  1  lnx+1+ +1 x−(x+1)lnx+x+e      x  x−lnx+1−e g(x)= = x2 x2 1 令 h(x)= x−lnx+1−e,h(x)=1− , x h(x) 在   1 ,1   上单调递减; ( 1,e2  上单调递增 e  1 1 1  1 而 h   = +2−e0 ,当 x  ,1  时, h(x)h   0 , e e e  e 当 x ( 1,e2  时,注意到 h(x) 单调递增且 h(e)=0 1  当  xe 时, h(x)0,g(x)0,g(x) 单调递减; e 当 e xe2 时, h(x)0,g(x)0,g(x) 单调递增 e+1+e+e 1 1 1 g(x) = g(e)= =3+ ,b3+ ,b =3+ min e e e max e (3) (x)=ex(x+lnx) ,要证: (s+t)(s)+(t) 只需证: (x+t)−(x)−(t)0 ,其中 x,t 1 令 F(x)=(x+t)−(x)−(t),x1,F(x)=(x+t)−(x) 学科网（北京）股份有限公司 1  1  而 (x)=ex(x+lnx)+  1+  ex =ex  x+ +lnx+1  ,x1  x  x   2 1  (x)=ex  x+ +lnx− +2  0,(x) 在 (1,+) 上单调递增  x x2  而 x+t  x1,(x+t)−(x)0,F(x)0,F(x) 在 (1,+) 上单调递增 F(x) F(1)=(1+t)−(1)−(t)=(1+t)−(t)−e 下只需证: (1+t)−(t)−e0,t 1 ,令 G(t)=(1+t)−(t)−e,t 1 G(t)=(1+t)−(t)0,G(t) 在 (1,+) 上单调递增, G(t)G(1)=(2)−(1)−e ,只需证: (2)−(1)−e0 , 而 (2)−(1)−e=e2(2+ln2)−2e0 显然成立 (x+t)(x)+(t) 对 x,t 1 恒成立,令 x=s(s+t)(s)+(t) . 学科网（北京）股份有限公司