文档内容
2024 届高三暑假作业检测试卷
数学
本试卷共8页.时量120分钟.满分150分.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 , ,则 ( )
A. B. C. D.
2. 已知 ( 为虚数单位),其中 , 为实数,则 , 的值分别为( )
A. ,1 B. 1, C. 1,1 D. ,
3. 设P是双曲线 上一点,F,F 分别是双曲线左、右两个焦点,若|PF|=9,则|PF|等于(
1 2 1 2
)
A. 1 B. 17 C. 1或17 D. 8
4. 为了庆祝中国共产党第二十次全国代表大会,学校采用按比例分配的分层随机抽样的方法从高一1002
人,高二1002人,高三1503人中抽取126人观看“中国共产党第二十次全国代表大会”直播,那么高三年
级被抽取的人数为( )
A. 36 B. 42 C. 50 D. 54
5. 一个圆锥的侧面展开图是圆心角为 ,弧长为 的扇形,则该圆锥轴截面的面积 ( )
A. B. C. D.
6. 已知 , , , ,则 的值为(
)
A. B. C. D.
7. 某学生进行投篮训练,采取积分制,有7次投篮机会,投中一次得1分,不中得0分,若连续投中两次
则额外加1分,连续投中三次额外加2分,以此类推,连续投中七次额外加6分,假设该学生每次投中的概率是 ,且每次投中之间相互独立,则该学生在此次训练中恰好得7分的概率是( )
A. B. C. D.
8. 设 , , ,则( )
A. B.
C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知 是两条不重合的直线, 是两个不重合的平面,下列命题不正确的是( )
.
A 若 , , , ,则
B. 若 , , ,则
.
C 若 , , ,则
D. 若 , , ,则
10. 已知圆 ,以下四个结论正确的是( )
A. 过点 与圆M相切的直线方程为
B. 圆M与圆 相交
C. 过点 可以作两条直线与圆M相切
D. 圆M上的点到直线 的距离的最大值为3
11. 在平面直角坐标系 中,点 是抛物线 的焦点,两点 、
在抛物线 上,则下列说法正确的是( )A. 抛物线 的方程为
B.
C. 以 为直径的圆的方程是
D. 、 、 三点共线
12. 定义在 上的函数 的导函数为 ,且 ,则对任意 ,下列结论成立
的是( )
A .
B.
C. 不存在 ,使得
D. 存在 ,使得
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知 , ,则 __________.
14. 设等差数列 的前 项和为 ,已知 ,则 __________.
15. 已知函数 ,则 ______.
16. 当 时,不等式 恒成立,则实数a的取值范围是____.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知 分别为 内角 的对边,且 .
(1)求角 ;
(2)若 , 的面积为 ,求 的值.18. 已知数列 的前 项和为 , , .
(1)求数列 的通项公式;
(2)若 ,数列 的前 项和为 ,求 .
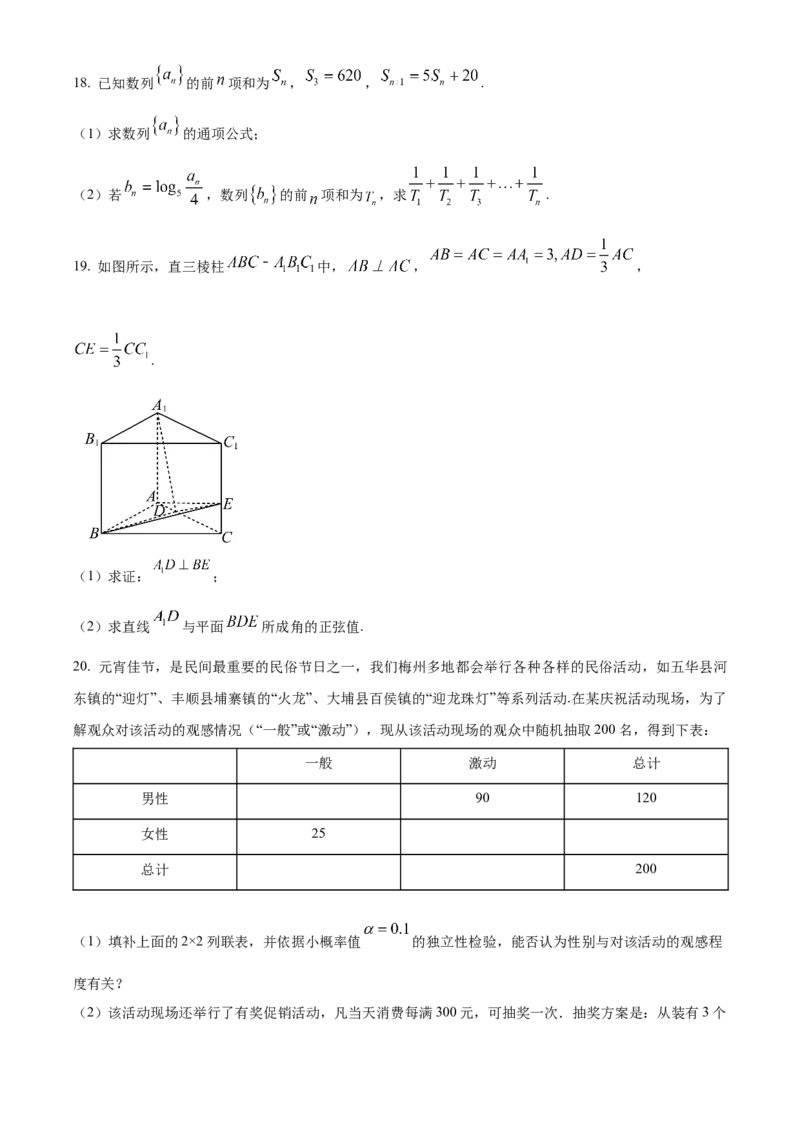
19. 如图所示,直三棱柱 中, , ,
.
(1)求证: ;
(2)求直线 与平面 所成角的正弦值.
20. 元宵佳节,是民间最重要的民俗节日之一,我们梅州多地都会举行各种各样的民俗活动,如五华县河
东镇的“迎灯”、丰顺县埔寨镇的“火龙”、大埔县百侯镇的“迎龙珠灯”等系列活动.在某庆祝活动现场,为了
解观众对该活动的观感情况(“一般”或“激动”),现从该活动现场的观众中随机抽取200名,得到下表:
一般 激动 总计
男性 90 120
女性 25
总计 200
(1)填补上面的2×2列联表,并依据小概率值 的独立性检验,能否认为性别与对该活动的观感程
度有关?
(2)该活动现场还举行了有奖促销活动,凡当天消费每满300元,可抽奖一次.抽奖方案是:从装有3个红球和3个白球(形状、大小、质地完全相同)的抽奖箱里一次性摸出2个球,若摸出2个红球,则可获
得100元现金的返现;若摸出1个红球,则可获得50元现金的返现;若没摸出红球,则不能获得任何现金
返现.若某观众当天消费600元,记该观众参加抽奖获得的返现金额为X,求随机变量X的分布列和数学
期望.
附: ,其中 .
0.100 0.050 0.010 0.001
.
2.706 3.841 6.635 10 828
21. 已知椭圆 的左、右焦点分别为 ,点 是椭圆 的上顶点, 是
等边三角形, 的内切圆的面积为 .
(1)求椭圆 的方程;
(2)已知 在 轴负半轴上且 ,过 的直线与椭圆交于 , 两点,求 面积的
最大值.
22. 已知函数 .
的
(1)若 在 处 切线方程平行于直线 ,求 的值以及此时的切线方程;
(2)若方程 在 上有两个不同的实数根,求实数 的取值范围.