贵阳第一中学2024届高考适应性月考卷（一）数学-答案_2023年9月_01每日更新_22号_2024届贵州省贵阳市第一中学高考适应性月考（一）

贵阳第一中学 2024 届高考适应性月考卷（一） 数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项是符合题目要求的） 题号 1 2 3 4 5 6 7 8 答案 A C D B D C A B 【解析】 x1 1．函数yln(1x)的定义域为(，1)，不等式 ≤0，可化为x(x1)≤0且x0，所以 x 0x≤1，所以AB{x|0x1}，故选A． 1 1 x2 1 2．当x0时由基本不等式可得x ≥2，当且仅当x 时取得“=”，当 ≥2时，则 x x x x2 1 x2 2x1 (x1)2 x2 1 2≥0，可得 ≥0，即 ≥0，解得x0；所以“x0”是“ ≥2” x x x x 的充要条件，故选C． 3．对于A，由正态分布曲线对称性可知：P(X≥10)0.5，P(8≤X ≤12)2P(8≤X ≤10)， A正确；C正确，对于B，∵P(X≥8)P(X ≤12)，∴P(X ≤8)P(X ≤12)P(X ≤8) P(X≥8)1，B正确；对于D，∵D(X)22 4，∴D(2X 1)4D(X)16，D错误， 故选D． 4．当x0时，f(x)0，排除A选项；因为 f(x) f(x)，xR，所以 f(x)为偶函数，排除 2xsinx(x2 1)cosx π C；当x0时， f(x) ，0x≤ 时，2xsinx(x2 1)cosx0， e2 2  π π π  所以 f(x)在区间0，  单调递增； f  0，f(π)0，所以存在m ，π，使得  2 2 2  f(m)0，故 f(x)在(0，m)上单调递增，在(m，π)上单调递减，排除D，故选B． 5．当a0时，满足题意；当为二次函数时，因为 f(x)ax2 2(a1)x2在(，4)上为减 a0，  1  1 函数，所以1a 解得0a≤ ，综上所述a的取值范围为  0，  ，故选D．  ≥4， 5  5  a 数学参考答案·第1页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}x2 y2 b 6．双曲线  1(a0，b0)的渐近线方程为y x，记点A(0，3c)，由题意可知，点 a2 b2 a x2 y2 b F(c，0)为双曲线  1(a0，b0)的右焦点，易知直线AF 与直线y x垂直，且 a2 b2 a b 1 c b 2 1 2 10 k AF 3，可得 a  3 ，因此，该双曲线的离心率为e a  1 a    1 3    3 ， 故选C． 7．因为2a log a22b log b122b log (2b)，令 f(x)2x log x，其中x0，因为函 2 2 2 2 数y2x、ylog x在(0，)上均为增函数，所以，函数 f(x)2x log x在(0，)上 2 2 为增函数，因为2a log a22b log (2b)，即 f(a) f(2b)，故2ba0，则2ba0， 2 2 所以，2ba11，则ln(2ba1)ln10，B错A对；无法确定|a2b|与1的大小， 故ln|a2b|与0的大小无法确定，CD都错，故选A． f(x)1 f(x)ex [f(x)1]ex f(x) f(x)1 8．构造函数 F(x) ，则 F(x)  ，因为 ex e2x ex f(x)1 f(x) f(x)1，所以F(x)0恒成立，故F(x) 单调递减， f(x)12023ex变 ex f(x)1 f(0)1 形为 2023，又 f(0)2022，所以F(0) 2023，所以F(x)F(0)，解 ex e0 得：x0，故选B． 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有 多项符合题目要求，全部选对的得5分，选对但不全的得2分，有选错的得0分） 题号 9 10 11 12 答案 BD CD ABC AD 【解析】 5 1 2 1 3 9．由题意知A，A ，A 两两互斥，故D正确；又P(A)  ，P(A )  ，P(A ) ， 1 2 3 1 10 2 2 10 5 3 10 5 4 4 P(B|A) ，P(B|A ) ，P(B|A ) ，故B正确；P(B)P(AB)P(A B) 1 11 2 11 3 11 1 2 1 5 1 4 3 4 9 P(AB)P(A)P(B|A)P(A )P(B|A )P(A )P(B|A )        ，故 3 1 1 2 2 3 3 2 11 5 11 10 11 22 1 5 5 A错误；因为P(BA)P(B|A)P(A)   P(B)P(A)，所以B与A不是相互独立 1 1 1 2 11 22 1 1 事件，故C错误，故选BD． 数学参考答案·第2页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}10．数列{a }各项乘以10后再减4得到数列{b }：0，3，6，12，24，48，96，192，，故该数列从 n n 0，n1， 第2项起构成公比为2的等比数列，所以b  数列{b }的第2023项为 n 32n2，n≥2， n b 4 0.4，n1， 322021，故 A 错误；从而a  n  故 B 错误；当n1时， n 10 0.32n2 0.4，n≥2， S a 0.4；当n≥2时，S  a a a 0.40.3(20 212n2)0.4(n1) 1 1 n 1 2 n 12n1 0.4n0.3 0.4n0.32n10.3 ，当 n1时， S 0.4 也符合上式，所以 12 1 S 0.4n0.32n10.3 ， S 40.329 0.3157.3 ， 故 C 正 确 ； 因 为 n 10 0，n1， nb  所以当n1时，T b 0，当n≥2时，T b 2b 3b  n 3n2n2，n≥2， 1 1 n 1 2 3 nb 03(220 321422 n2n2)，2T 3(2213 22 423 n n n  22n1  2n1)，所以T 03(2 2122 2n2 n2n1) 32 n2n1  n  12  3(1n)2n1 ， 所 以 T 3(n1)2n1 ， 又 当 n1 时 T 0 也 满 足 上 式 ， 所 以 n 1 T 3(n1)2n1，故D正确，故选CD. n 11．对于 A，令x y0，得 f(0) f(0) f(0)0，故 A 正确；对于 B，令 yx得：  2x   2x  f(x) f(x) f  （1），再以x代x，得： f(x) f(x) f  （2），（1） 1x2  1x2   2x   2x   2x   2x  （2）得： f   f  0，∴f  f  ，∴定义在(1，1)上的函 1x2  1x2  1x2  1x2  数 f(x)为奇函数，故 B 正确；对于 C，∵函数 f(x)为定义在(1，1)上的奇函数，且当  x x  x(1，0) 时， f(x)0，不妨设1x x 1，则 f(x ) f(x ) f  1 2  ，因为 1 2 1 2 1xx  1 2 x x x x (1x )(1x ) x x 1x x 1，所以 1 2 0且 1 2 1 1 2 0，因此1 1 2 0， 1 2 1xx 1xx 1xx 1xx 1 2 1 2 1 2 1 2  x x  所以 f  1 2 0，则 f(x ) f(x )0，即 f(x ) f(x )，故函数 f(x)在(1，1)上为 1xx  1 2 1 2 1 2 7 2  x y  增函数，C 正确；对于 D，令 x ，y ，因为 f(x) f(y) f   ，则 8 3 1xy 7 2 1 2 1 7 7 7 f   f   f  ，即 f   f   f  ，因为  ，且函数 f(x)在(1，1)上 8 3 2 3 2 8 8 9 数学参考答案·第3页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}7 7 2 1 7 7 为增函数，所以 f   f  ，即 f   f   f   f  ，故D错误，故选ABC． 8 9 3 2 8 9 x2 y2 3 12．因为双曲线C的方程为  1，所以a4，b3，c5，渐近线方程为y x，选 16 9 4  3 3 项A，因为直线PF 与双曲线有两个交点，所以k ，  ，即A正确；选项B，由双 2  4 4 曲线的定义知，|PF ||PF |2a8，若mn，则|PF |2 |PF |2|FF |2(2c)2 1 2 1 2 1 2 100 ， 因 为 (|PF ||PF |)2 |PF |2 |PF |2 2|PF ||PF | ， 所 以 1 2 1 2 1 2 641002|PF ||PF |，解得|PF ||PF |18，即B错误；选项C：|PF ||PQ| 1 2 1 2 2 |FQ|2|PQ|2a52|PQ|5，即C错误；选项D，因为PT 平分FPF ，由角分线 1 1 2 |PF | |PF | |PF | |TF | 51 3 定理知， 1  2 ，所以 1  1   ，又 |PF ||PF |8 ，所以 |TF | |TF | |PF | |TF | 51 2 1 2 1 2 2 2 3 |PF ||PF |8，解得|PF |16，即D正确，故选AD. 2 2 2 2 三、填空题（本大题共4小题，每小题5分，共20分） 题号 13 14 15 16 1  2  16 2 3 3 3 4 n1 答案 480 1， 1 ；     2  e  3 5 20 9 【解析】 13．(x2y1)6的展开式中为x2y3项为C2x2C3(2y)3 480x2y3． 6 4 1 1  1  14．令4x11，即x ，得y2，故P ，2 ，由P ，2 在直线l：axby30(b0) 2 2  2  1 上，得 a2b30，即a24b8，因为a0且a1，b0，所以a22，所以 2 1 1  1 1  1 1 4b a2 1 4b a2 1    (a24b)  2   ≥   22     ， a2 4b a2 4b 8 8 a2 4b  8  a2 4b  2 4b a2 当且仅当  ，即a24b4，即a2，b1时，等号成立． a2 4b 1 1 15 ． 由 f(x)xlnx (m1)x2 x1 ， 得 f(x)lnx (m1)x ， x0 ． 要 使 4 2 1 1 f(x)xlnx (m1)x2 x1有两个极值点，只需 f(x)lnx (m1)x有两个变号根， 4 2 数学参考答案·第4页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}1 lnx lnx 1lnx 即 (m1) 有两个变号根．令g(x) (x0)，则g(x) ，由g(x)0得 2 x x x2 xe，易知当x(0，e)时，g(x)0，此时g(x)单调递增；当x(e，)时，g(x)0， 1 此时g(x)单调递减．所以g(x) g(e) ， max e 1 而g e0，当0x1时，g(x)0，当 e 1 x1时，g(x)0，作出yg(x)，y (m1) 2 1 1 的图象如图 1，可知：0 (m1) ，解得 2 e 图1 2  2  1m 1．故答案为 1， 1 ． e  e  16．记第n个图形为P ，边长为a ，边数为b ，周长为L ，面积为S ，P有b 条边，边长a ； n n n n n 1 1 1 1 1 2 P 2 有b 2 4b 1 条边，边长a 2  3 a 1 ；P 3 有b 3 42b 1 条边，边长a 3  3   a 1 ；……分析可知 1 1 n1 a n  3 a n1 ，即a n  3   a 1 ；b n 4b n1 ，即b n b 1 4n1.当第1个图中的三角形的边长为 1 n1 4 n1 1 时，即 a 1 1 ， b 1 3 ，所以 L n a n b n  3   34n1 3 3   ，当 n3 时， 4 31 16 L 3 3 3    3 .由图形可知 P n 是在 P n1 每条边上生成一个小三角形，即 3 3 3 S S b  a2，(n≥2)，即S S  a2 b ，S S  a2 b ， n n1 n1 4 n n n1 4 n n1 n1 n2 4 n1 n2 3 3 ，S S  a2 b ，利用累加法可得S S  (a2 b a2 b a2 b)， 2 1 4 2 1 n 1 4 n n1 n1 n2 2 1 1 数列{a }是以 为公比的等比数列，数列{b }是以4为公比的等比数列，故{a2 b }是以 n 3 n n n1 4 1 3 为公比的等比数列，当第 1 个图中的三角形的边长为 1 时，S  a2sin60 ， 9 1 2 1 4  4 n1 a2 1，a2  1 ，P有b 3条边，则a2 b a2 b a2 b  a 2 2 b 1    1 9      1 2 9 1 1 n n1 n1 n2 2 1 4 1 9 数学参考答案·第5页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}1  4 n1  9 3    1 1    4 9       5 3     1   9 4    n1     ， 所 以 S n S 1  3 20 3     1   9 4    n1     ， 所 以 9 2 3 3 3 4 n1 3 S      ，S  也满足上式． n 5 20 9 1 4 四、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分10分） 1 2a 1 1  1  （1）证明：由题意知：  n 2 1， 12 1， a a a a a  n1 n n n1 n  1  1 所以数列 1是以2为公比， 12为首项的等比数列． a  a n 1 ……………………………………………………………………………………………（5分） 1 1 （2）解：由（1）知 12n  2n 1， a a n n 1 1 1 2(12n) 所以    n2n1n2， a a a 12 1 2 n 记 f(n)2n1n2，显然 f(n)为递增数列，又 f(9)1031，f(10)2056， 所以最大整数n9． ………………………………………………………（10分） 18．（本小题满分12分） 5 5 解：（1）由题意可得，x3，y2，(x x)(y  y)4.8，(x x)2 10， i i i i1 i1 5 (x x)(y  y) i i 设y关于x的经验回归方程为yˆ b  xaˆ，则b   i1 0.48， 5 (x x)2 i i1 aˆ yb  x20.4830.56，∴y关于x的经验回归方程为yˆ 0.48x0.56． …………………………………………………………………………（6分） （2）零假设为H ：两个店的顾客购买率无差异，则 0 由题意可知2×2列联表如表所示： 购买 不购买 合计 分店一 180 120 300 分店二 150 50 200 合计 330 170 500 …………………………………………………………………………（8分） 数学参考答案·第6页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}500(18050150120)2 ∴2  12.03210.828， 300200330170 ∴根据小概率值0.001的独立性检验，没有充分证据推断H 成立， 0 即两个店的顾客购买率有差异，且推断犯错的概率不超过0.001． …………………………………………………………………………（12分） 19．（本小题满分12分） （1）证明：因为E，F 为圆弧AB上的两个三等分点，所以EF∥ABEF∥平面ABCD， 同理EH∥平面ABCD，又EFEH E ，所以平面ABCD∥平面EFGH， 又平面平面ABCDCP，平面平面EFGH MQ，所以CP∥MQ． …………………………………………………………………………（6分） （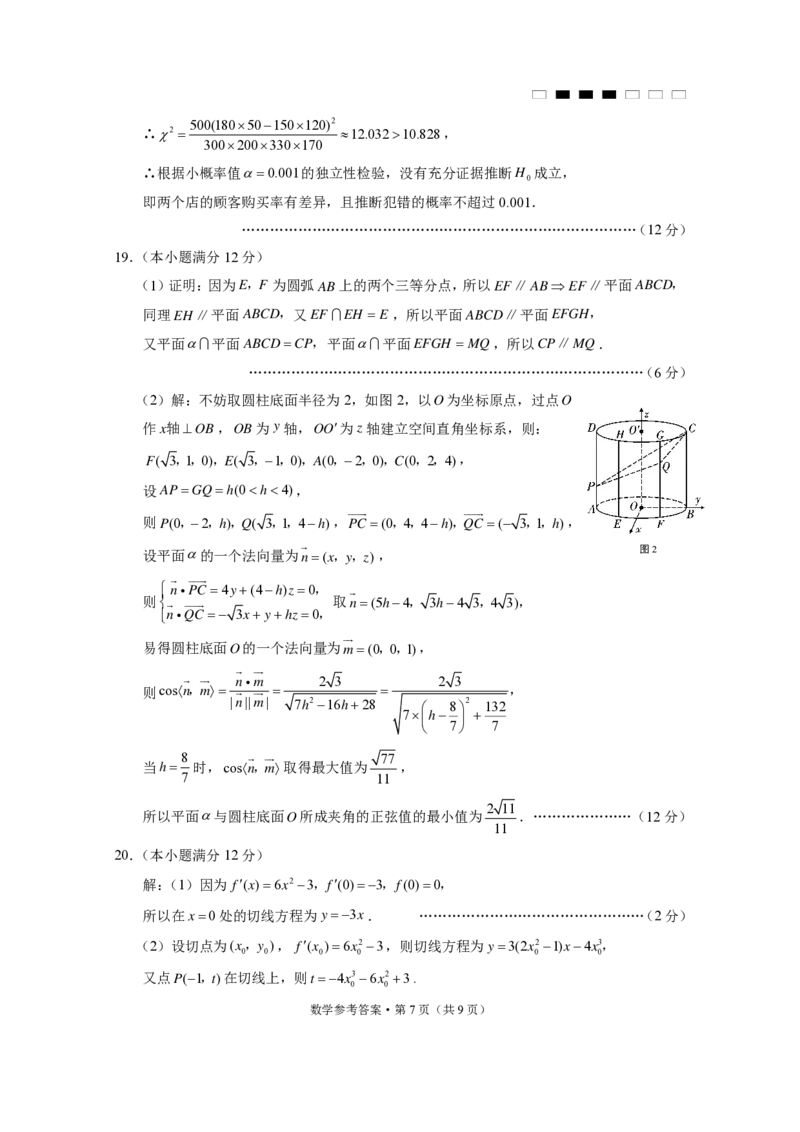2）解：不妨取圆柱底面半径为2，如图2，以O为坐标原点，过点O 作x轴OB，OB为y轴，OO为z轴建立空间直角坐标系，则： F( 3，1，0)，E( 3，1，0)，A(0，2，0)，C(0，2，4)， 设APGQh(0h4)，   则P(0，2，h)，Q( 3，1，4h)，PC (0，4，4h)，QC ( 3，1，h)，  设平面的一个法向量为n(x，y，z)， 图2   nPC 4y(4h)z0，  则  取n(5h4， 3h4 3，4 3)， nQC  3x yhz0，  易得圆柱底面O的一个法向量为m(0，0，1)，     nm 2 3 2 3 则cosn，m     ， |n||m| 7h2 16h28  8 2 132 7h    7 7 8   77 当h 时，cosn，m取得最大值为 ， 7 11 2 11 所以平面与圆柱底面O所成夹角的正弦值的最小值为 ．…………………（12分） 11 20．（本小题满分12分） 解：（1）因为 f(x)6x2 3，f(0)3，f(0)0， 所以在x0处的切线方程为y3x． …………………………………………（2分） （2）设切点为(x，y )， f(x )6x2 3，则切线方程为y3(2x2 1)x4x3， 0 0 0 0 0 0 又点P(1，t)在切线上，则t 4x3 6x2 3. 0 0 数学参考答案·第7页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}令g(x )4x3 6x2 3，g(x )12x2 12x 12x (x 1)， 0 0 0 0 0 0 0 0 则在(，1)，(0，)上，g(x )0，g(x )递减； 0 0 在(1，0)上，g(x )0，g(x )递增. 0 0 g(1)1，g(0)3，所以t(1，3). …………………………………………（7分） （3）过点A(0，0)，B(1，1)分别存在1条直线与曲线y f(x)相切； 过点C(1，3)，D(1，1)分别存在2条直线与曲线y f(x)相切； 过点E(1，2)存在3条直线与曲线y f(x)相切．…………………………………（12分） 21．（本小题满分12分） 1 2 （1）解：由题意可知a  ，b  ， …………………………………………（2分） 1 3 1 3 1 2 1 1 2 1 1 2 1 5 从而a  a   b  ，b  a     b  ． ……………………（4分） 2 3 1 3 2 1 3 2 3 1 3 2 3 2 1 9 （2）证明：由题意知P(X 2)a ，P(X 1)b ，P(X 0)1a b， n n n n n n n 1 2 1 1 1 由全概率公式得：a  a   b 0(1a b ) a  b，① n1 3 n 3 2 n n n 3 n 3 n 2 2 1 1 1 1 1 b  a     b 1(1a b ) a  b 1，② n1 3 n 3 2 3 2 n n n 3 n 2 n ①×2＋②得： 1 1 1 6 1 6 2a b  a  b 1 (2a b )1 2a b   2a b   ， n1 n1 3 n 6 n 6 n n n1 n1 5 6 n n 5 6 2a b  n1 n1 5 1 即：  ， 6 6 2a b  n n 5  6 1 6 2 即2a b  是以 为公比，以2a b   为首项的等比数列．  n n 5 6 1 1 5 15 ……………………………………………………………………………………………（8分） 6 2 1 n1 （3）解：由（2）知：2a b     ， n n 5 15 6 2 1 n1 6 所以E(X )2a b 0(1a b )     ．……………………………（12分） n n n n n 15 6 5 数学参考答案·第8页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}22．（本小题满分12分） 3 p p2 （1）解：直线l：y x  ，联立抛物线方程得：x2 7px 0， 3  2 4 设A(x，y )，B(x，y )，所以x x 7p，则|AB|x x  p8p16 p2， 1 1 2 2 1 2 1 2 所以抛物线C的标准方程为y2 4x，准线方程为x1．…………………………（6分） y2 4x， （2）证明：设直线l：xmy1，则  y2 4my40， xmy1 所以y  y 4m，y y 4， 1 2 1 2 y 4 4  8  8 又k  1  ，l ：y x，所以M2， ，同理N2， ， OA x 1 y 1 OA y 1  y 1   y 2   8  8  设圆上任意一点为P(x，y)，则圆的方程为：(x2)2 y y 0，  y  y  1 2  1 1  64 化解得：(x2)2  y2 8  y (x2)2  y2 8my160，  y y  y y 1 2 1 2 令y0x2或x6，所以以MN 为直径的圆过定点(2，0)和(6，0)． …………………………………………………………………………………（12分） 数学参考答案·第9页（共9页） {#{QQABYQKEogCIABBAAAhCEQECCEAQkBAACKoOgEAIoAAAgQFABCA=}#}