文档内容
高2021级数学(文科)答案
1.已知集合 , ,则 ( )
A. B.
C. D.
【答案】A
【分析】根据一元二次不等式的求解方法,结合集合的交集,可得答案.
【详解】由不等式 ,分解因式可得 ,解得 ,则
,
所以 .
故选:A.
2.已知 (i为虚数单位),则复数 在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】B
【分析】由已知等式求出复数 ,得到复数 ,由复数的几何意义得 在复平面内对应
的点所在象限.
【详解】由 ,得 ,则 ,在复平面内对应的点位于第
二象限.
故选:B
3.抛物线 的准线方程是( )
A. B.
C. D.
【答案】A
【分析】先化为标准型,利用抛物线的准线方程可得答案.
试卷第1页,共3页
学科网(北京)股份有限公司【详解】因为 ,所以 ,所以准线方程为 .
故选:A.
4.已知函数 ,则 ( )
A. B.2 C. D.3
【答案】C
【分析】利用分段函数的定义代入求值即可.
【详解】由题意可得: .
故选:C.
5.已知 满足约束条件 ,则目标函数 的最小值是( )
A.1 B.2 C.11 D.无最小值
【答案】A
【分析】作出可行域,将目标函数变为 ,通过平移直线 即可求出 的
最小值.
【详解】根据题意,可行域如图所示:将直线 平移至刚好经过 时, 取的最
小值: .
故选:A.
6.下列函数中,既是 上的增函数,又是以 为周期的偶函数的是( )
试卷第2页,共3页A. B. C. D.
【答案】D
【分析】利用函数的奇偶性、在指定区间上的单调性逐项判断作答.
【详解】显然函数 、 都是奇函数,AC不是;
当 时, ,而函数 在 上单调递减,函数 在
上单调递减,B不是;
函数 是周期为 的偶函数,当 时, ,为原函数,即
在 上递增,D是.
故选:D
7.定义在R上的奇函数 满足 是偶函数,当 时, ,
则 ( )
A. B. C.0 D.2
【答案】C
【分析】根据题意,由函数奇偶性的性质分析可得 ,进而可得
,即函数 是周期为4的周期函数,从而利用周期性即可求
解.
【详解】根据题意,函数 是定义在 上的奇函数,则 ,且 ,
又函数 是偶函数,则 ,变形可得 ,
则有 ,进而可得 ,
所以函数 是周期为4的周期函数,
则 .
故选:C.
8.用半径为10cm,圆心角为 的扇形围成一个圆锥的侧面,这个圆锥的体积为
( )
试卷第3页,共3页
学科网(北京)股份有限公司A. B.128 C. D.96
【答案】C
【分析】根据题意确定圆锥的母线长,根据扇形的弧长求出圆锥的底面半径和高,根
据圆锥体积公式即可求得答案.
【详解】设圆锥的底面半径为R,由题意可知圆锥母线长为 ,
由题意可得 ,
故圆锥的高为 ,
故圆锥的体积为 ,
故选:C
9.下列说法正确的有( )
①对于分类变量 与 ,它们的随机变量 的观测值 越大,说明“ 与 有关系”
的把握越大;
②我校高一、高二、高三共有学生 人,其中高三有 人.为调查需要,用分层
抽样的方法从全校学生中抽取一个容量为 的样本,那么应从高三年级抽取 人;
③若数据 、 、 、 的方差为 ,则另一组数据 、 、 、 的方差
为 ;
④把六进制数 转换成十进制数为: .
A.①④ B.①② C.③④ D.①③
【答案】A
【分析】利用独立性检验可判断①;利用分层抽样可判断②;利用方差公式可判断③;
利用进位制之间的转化可判断④.
【详解】对于①,对于分类变量 与 ,它们的随机变量 的观测值 越大,说明“
与 有关系”的把握越大,①对;
对于②,由分层抽样可知,应从高三年级抽取的人数为 ,②错;
对于③,记 ,则 ,
所以,数据 、 、 、 的平均数为
试卷第4页,共3页,
其方差为
,③错;
对于④,把六进制数 转换成十进制数为: ,④对.
故选:A.
10.已知函数 的部分图象如图所示,若将函
数 的图象向右平移 个单位,得到函数 的图象,则( )
A. B.
C. D.
【答案】C
【分析】利用函数图象可求出 的解析式为 ,再根据平移规则
可得 .
【详解】由图象可知, ,解得 ;
由振幅可知 ;
将 代入可得 ,又 ,即可得 ,
因此 ,
试卷第5页,共3页
学科网(北京)股份有限公司易知 ,
故选:C.
11.人们用分贝 来划分声音的等级,声音的等级 (单位: )与声音强度
(单位: )满足 .一般两人小声交谈时,声音的等级约为
,在有50人的课堂上讲课时,老师声音的等级约为 ,那么老师上课时声音
强度约为一般两人小声交谈时声音强度的( )
A.1倍 B.10倍 C.100倍 D.1000倍
【答案】C
【分析】根据所给声音等级与声音强度的函数关系,求出声音等级即可比较得解.
【详解】∵声音的等级式 (单位: )与声音强度 (单位: )满足
,
又∵老师的声音的等级约为63dB,
,解得 ,即老师的声音强度约为 ,
∵两人交谈时的声音等级大约为 ,
,解得 ,即两人交谈时的声音强度约为 ,
老师上课时声音强度约为两人小声交谈时声音强度的 倍.
故选:C
12.函数 的定义域为 ,当 时, 且 ,若函
数 有四个不同的零点,则实数 的取值范围为( )
A. B. C. D.
【答案】A
【分析】将 在 上的图象每次向右平移2个单位,且纵坐标变为原来的一半,
试卷第6页,共3页得到 在 上的图象,根据 的图象与 有四个不同的交点,得到
的取值范围.
【详解】先作出 在 上的图象,根据 可知 在 上的图象
为 在 上的图象向右平移2个单位且纵坐标变为原来的一半得到,
同理得到 上的图象,如图:
函数 有四个不同的零点可看作 与 有四个不同的交点,
由图可知 ,故 .
故选:A.
13.已知等差数列 的前n项和为 ,若 ,则 .
【答案】35
【分析】根据等差数列的前n项和公式,及等差数列的性质求解即可.
【详解】解: 等差数列 的前n项和为 , ,
,
故答案为:35.
14.已知 , ,则 .
【答案】
【分析】本题首先可通过同角三角函数关系求出 ,然后根据二倍角公式即可
得出结果.
【详解】因为 , ,
所以 , ,
试卷第7页,共3页
学科网(北京)股份有限公司则 ,
故答案为: .
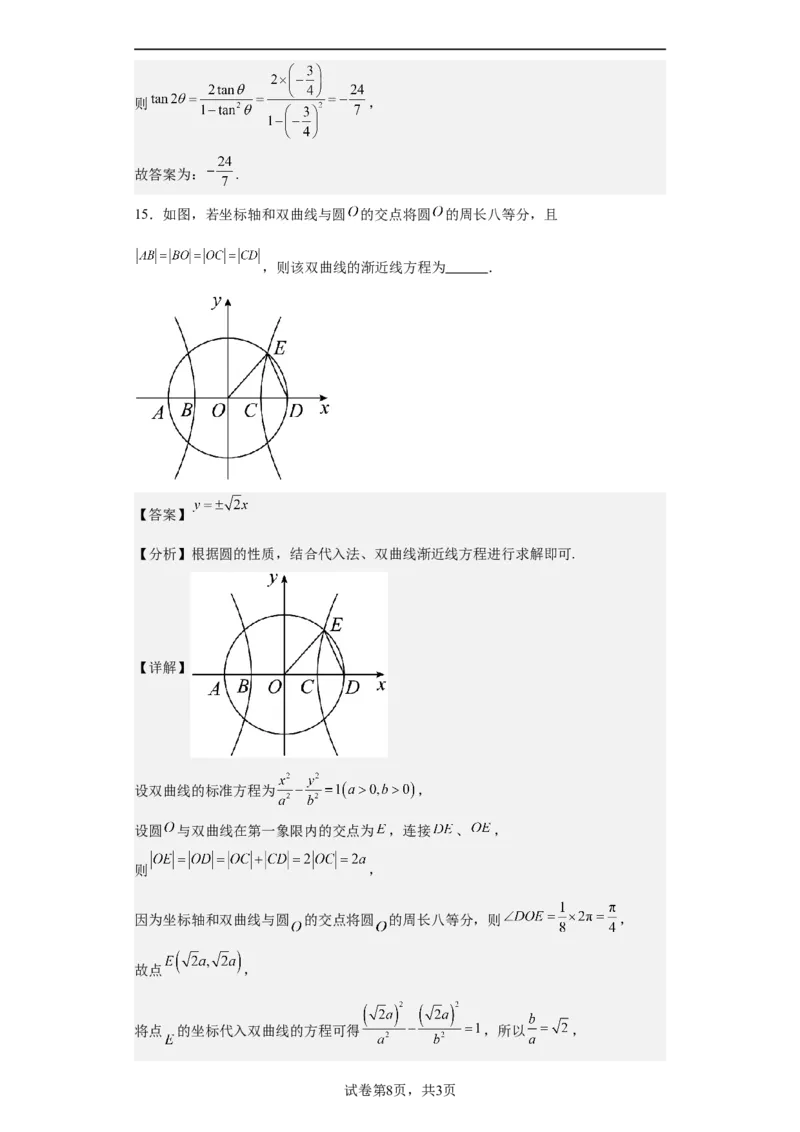
15.如图,若坐标轴和双曲线与圆 的交点将圆 的周长八等分,且
,则该双曲线的渐近线方程为 .
【答案】
【分析】根据圆的性质,结合代入法、双曲线渐近线方程进行求解即可.
【详解】
设双曲线的标准方程为 ,
设圆 与双曲线在第一象限内的交点为 ,连接 、 ,
则 ,
因为坐标轴和双曲线与圆 的交点将圆 的周长八等分,则 ,
故点 ,
将点 的坐标代入双曲线的方程可得 ,所以 ,
试卷第8页,共3页所以该双曲线的渐近线方程为 .
故答案为:
16.设函数 ,有下列结论:
① 的图象关于点 中心对称;
② 的图象关于直线 对称;
③ 在 上单调递减;
④ 在 上最小值为 ,
其中所有正确的结论是 .
【答案】②③
【分析】整理化简 解析式可得 ,根据正弦函数的相关性质
逐一进行判断即可.
【详解】
,
当 时, ,则 的图象关于点 中心对称,故①错误;
当 时, ,则 的图象关于直线 对称,故②正确;
由 ,得 ,
当 即 时,函数 单调递减,
则当 时,函数 单调递减,故③正确;
当 时, ,可知函数 在 上单调递增,
试卷第9页,共3页
学科网(北京)股份有限公司∴ 的最小值为 ,故④错误.
故答案为:②③.
17.最近,纪录片《美国工厂》引起中美观众热议,大家都认识到,大力发展制造业,
是国家强盛的基础,而产业工人的年龄老化成为阻碍美国制造业发展的障碍,中国应
未雨绸缪.某工厂有35周岁以上(含35周岁)工人300名,35周岁以下工人200名,为
研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名
工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“35周岁以上(含35
周岁)”和“35周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:
分别加以统计,得到如图所示的频率分布直方
图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名
“35周岁以下组”工人的概率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成
的列联表,并判断是否有95%的把握认为“生产能手与工人所在的年龄组有关”?
生产能手 非生产能手 合计
35岁以下
35岁以上
合计
附表:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
试卷第10页,共3页【答案】(1) ;(2)列联表见解析,有把握.
【分析】(1)分别计算样本中日平均生产件数不足60件的工人中35周岁以上组工人
个数与35周岁以下组工人个数,并分别做好标记,然后利用列举法以及古典概型计算
方法可得结果.
(2)分别计算“35周岁以上组”与“35周岁以下组”中的生产能手个数,然后列出
表格,并依据公式计算 ,可得结果.
【详解】(1)由已知得,
样本中有35周岁以上组工人60名,35周岁以下组工人40名,
所以,样本中日平均生产件数不足60件的工人中,
35周岁以上组工人有 (人),记为 ;
35周岁以下组工人有 (人),记为
从中随机抽取2名工人,所有可能的结果共有10种:
至少有一名“35周岁以下组”工人的可能结果共有7种:
.
故所求的概率:
(2)由频率分布直方图可知,在抽取的100名工人中,
“35周岁以上组”中的生产能手 (人),
“35周岁以下组”中的生产能手 (人),
据此可得 列联表如下:
生产能手 非生产能手 合计
35岁以下 10 30 40
35岁以上 30 30 60
试卷第11页,共3页
学科网(北京)股份有限公司合计 40 60 100
所以得:
所以有95%的把握认为“生产能手与工人所在的年龄组有关”
【点睛】本题考查频率分布直方图的应用,审清题意,同时识记公式,简单计算,属
基础题.
18.已知向量 ,函数 .
(1)求函数 的单调递增区间;
(2)在 中, 分别是角 的对边,且 , ,求
的周长.
【答案】(1) ;
(2) .
【分析】(1)利用向量数量积的坐标表示,二倍角公式、辅助角公式求出并化简 ,
再利用正弦函数单调性求解作答.
(2)由(1)求出 ,再利用余弦定理求解作答.
【详解】(1)依题意,
,
由 得: ,
所以函数 的单调递增区间是 .
(2)由(1)知, ,即 ,而 ,
则 ,于是 ,解得 ,
由余弦定理有 ,即
,
解得 ,
试卷第12页,共3页所以 的周长为 .
19.如图,在四棱锥 中,平面 平面 ,底面 为菱形,
为等边三角形,且 , , 为 的中点.
(1)若 为线段 上动点,证明: ;
(2)求点 与平面 的距离.
【答案】(1)证明见解析
(2)
【分析】(1)因 为线段 上动点,明显要证明 平面 ,利用线面垂直判
定定理,分别证明 , 即可;
(2)利用等体积变换求距离即得.
【详解】(1)
连接 , .
∵ 为等边三角形, , , ,
又 平面 平面 ,平面 平面 , 平面 ,
平面 ,
又 平面 , ,
, , ,
又 , 平面 , 平面 , ,
平面
又 平面 ,
(2)由(1)知 平面
试卷第13页,共3页
学科网(北京)股份有限公司平面 ,∴ .
由题意 ,
∴ , ,
∴ 中, ,
∴ 中, ,
∴ 中,由余弦定理得 ,
设点 到平面 的距离为 ,
则 即 ,
,
得 ,
故点 与平面 的距离为
20.已知椭圆 : 的左、右焦点分别为 , ,过 的直线 与
交于 , 两点, 的周长为8,且点 在 上.
(1)求椭圆 的方程;
(2)设直线 与圆 : 交于C,D两点,当 时,求
面积的取值范围.
【答案】(1)
(2)
【分析】(1)由 的周长结合椭圆的定义得出 ,再将 代入椭圆方
试卷第14页,共3页程,即可求出 ,进而得出椭圆的方程;
(2)设直线l的方程为 ,由点到之间距离公式及勾股定理得出 ,
设 , ,由直线 方程与椭圆方程联立,得出 和 ,代入
,设 , ,由 的单调性得
出值域,即可求出 的范围.
【详解】(1)因为 的周长为8,
所以 ,解得 ,
将点 的坐标代入椭圆方程 ,得 ,解得 ,
所以椭圆E的方程为 .
(2)由(1)知圆 的方程为 ,设直线l的方程为 ,
则圆心 到直线l的距离 ,
由 ,可得 .
设 , ,联立方程组 ,
消去x得 ,
试卷第15页,共3页
学科网(北京)股份有限公司则 , ,
所以 ,
设 ,则 ,
设 ,
易知 在 上单调递增,则 在 上单调递增,
因为 ,
所以 .
21.已知函数 , .
(1)当 时,求函数 在点 处的切线方程;
(2)若函数 有两个零点 , ,求实数 的取值范围;
(3)在(2)的条件下,证明: .
【答案】(1)
(2)
(3)证明见解析
试卷第16页,共3页【分析】(1)根据导数的几何意义,即可求解;(2)首先判断函数的单调性,以及
极值,根据函数的零点个数判断 ,再通过构造函数,根据函数的单调性,
以及零点,求解不等式的解集;(3)根据函数的单调性,转化为证明
,再构造函数 ,利用导数判断函数的单
调性,即可证明.
【详解】(1)当 时, ,
, , ,
所以函数 在点 处的切线方程为 ,即 ;
(2)函数 的定义域为 ,
,
当 时, 恒成立, 单调递增,所以 不可能有2个零点;
当 时,当 时, , 单调递增,
当 时, , 单调递减,
当 时, ,当 时, ,
所以要满足函数 有2个零点,只需 ,
即 ,
整理得 ,
设 ,函数的定义域为 ,
试卷第17页,共3页
学科网(北京)股份有限公司,所以 在定义域上单调递增,
且 ,则不等式 的解集为 ,
所以 的取值范围为 ;
(3)证明:由(2)知, ,则 ,
要证明 ,即证明 ,
不妨设 ,
因为 ,所以 ,
又 ,函数 在 上单调递增,
此时需证明 ,
当 , 时,
可得 ,
因为 ,即证明 ,
设 ,函数的定义域为 ,
,
所以 在 单调递增,则 ,
,所以 ,
试卷第18页,共3页又 在 上单调递增,所以 ,
即 ,命题得证.
【点睛】关键点睛:本题考查导数研究函数的性质,不等式,双变量,零点偏移问题,
本题第三问的关键是利用分析法转化为证明 ,再根据
,构造函数,即可证明.
22.数学中有许多美丽的曲线,如在平面直角坐标系xOy中,曲线E:
(如图),称这类曲线为心形曲线.以坐标原点O为极
点,x轴的正半轴为极轴建立极坐标系,当 时,
(1)求E的极坐标方程;
(2)已知P,Q为曲线E上异于O的两点,且 ,求 的面积的最大值.
【答案】(1)
(2)
【分析】(1)将 , 代入曲线E,化简可得答案;
(2)不妨设 , , , ,则
试卷第19页,共3页
学科网(北京)股份有限公司的面积 ,令 ,可得 ,再
利用配方计算可得答案.
【详解】(1)将 , 代入曲线E,
得 ,即 ,
所以,E的极坐标方程为 ;
(2)不妨设 , ,
即 , ,
则 的面积
由于 ,
令 ,
则 , ,
则 ,
故当 时, ,
即 的面积的最大值为 .
试卷第20页,共3页