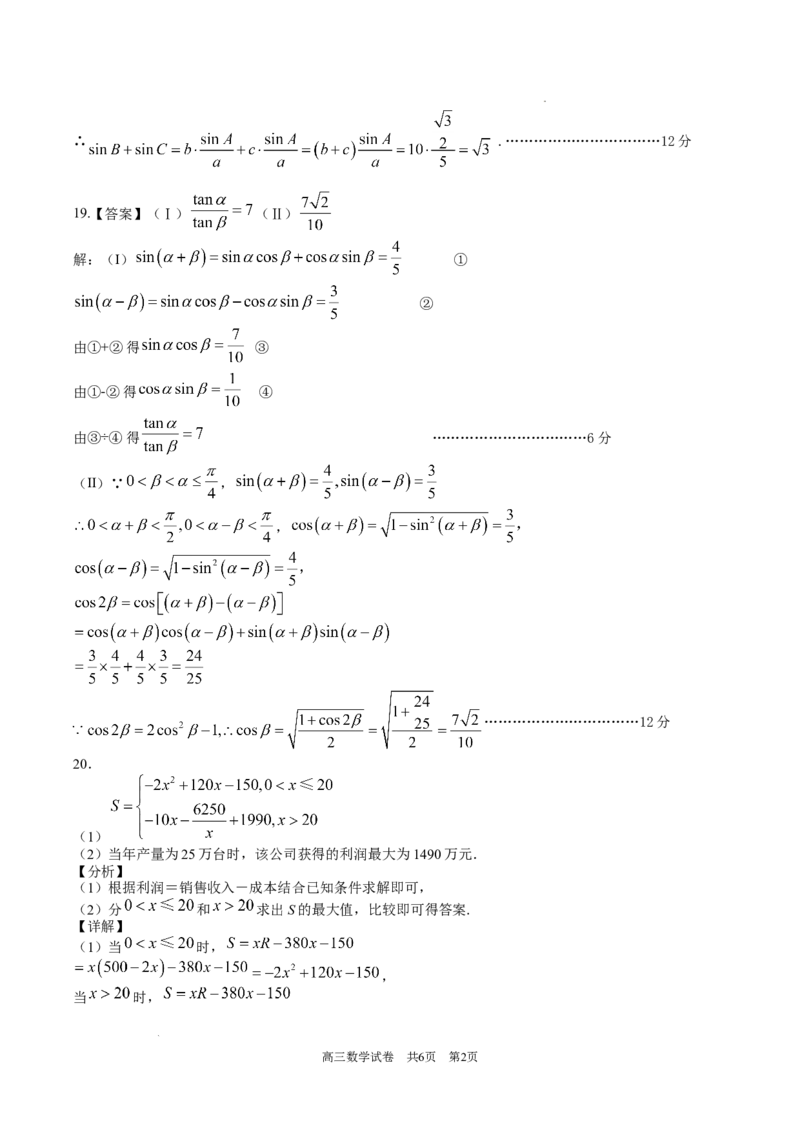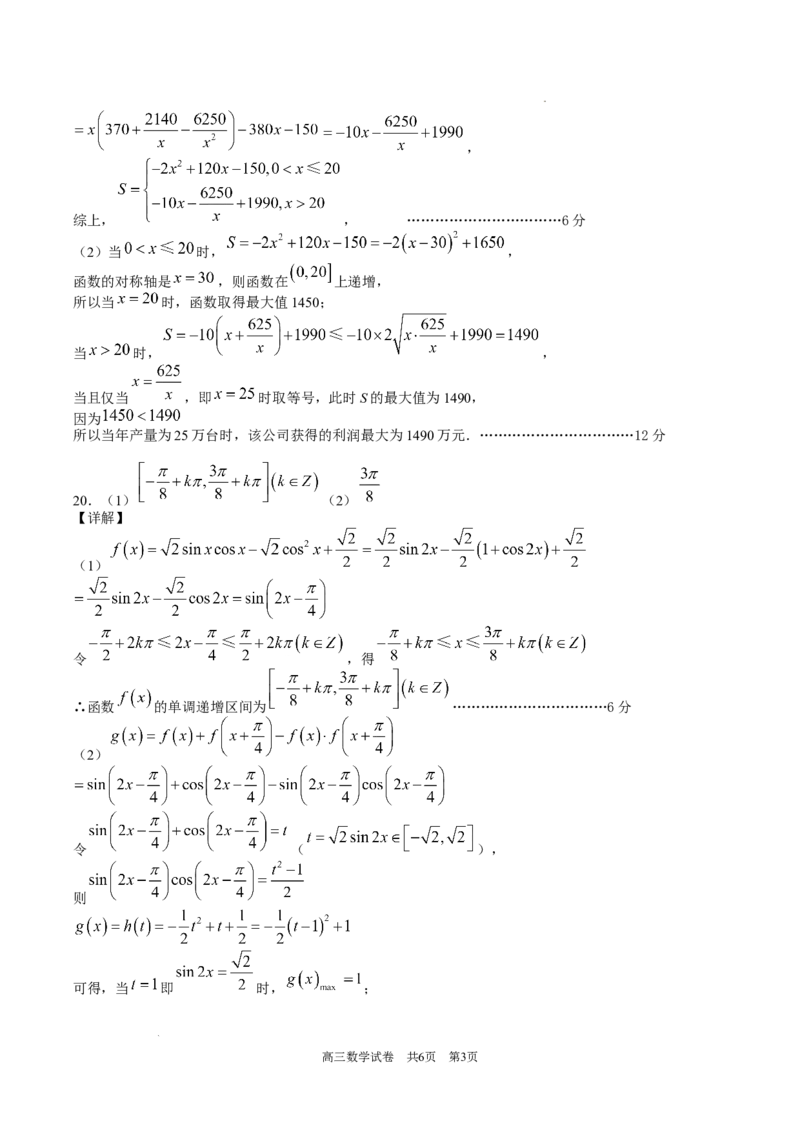文档内容
丰城中学2023-2024学年高三上学期10月段考
数学参考答案及解析
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A B C D B C C BCD ABC CD ACD
13. 14. 15. 4 16.
17.【小问1详解】
解不等式 ,得 ,即 ,
当 时,解不等式 ,得 ,即 ,
于是 或 ,
所以 或 .………………………………………5分
【小问2详解】
原不等式化为: ,解得 ,
于是 ,
由 是 的必要不充分条件,则集合 是 的真子集,得 且等号不同时成立,
解得 . ………………………………………10分
18.(1) ;(2) .
解析:(Ⅰ)因为 ,
所以由 ,即 ,
由正弦定理得 ,即 ,
∵ ,
∴ ,即 ,
∵ ,∴ ,∴ ,
∵ ,∴ . ………………………………………6分
(Ⅱ)∵ ,∴ ,
∵ , ,
∴ ,即 ,
高三数学试卷 共6页 第1页
学科网(北京)股份有限公司∴ .……………………………12分
19.【答案】(Ⅰ) (Ⅱ)
解:(I) ①
②
由①+②得 ③
由①-②得 ④
由③÷④得 ……………………………6分
(II)∵ ,
,
……………………………12分
20.
(1)
(2)当年产量为25万台时,该公司获得的利润最大为1490万元.
【分析】
(1)根据利润=销售收入-成本结合已知条件求解即可,
(2)分 和 求出S的最大值,比较即可得答案.
【详解】
(1)当 时,
,
当 时,
高三数学试卷 共6页 第2页
学科网(北京)股份有限公司,
综上, , ……………………………6分
(2)当 时, ,
函数的对称轴是 ,则函数在 上递增,
所以当 时,函数取得最大值1450;
当 时, ,
当且仅当 ,即 时取等号,此时S的最大值为1490,
因为
所以当年产量为25万台时,该公司获得的利润最大为1490万元.……………………………12分
20.(1) (2)
【详解】
(1)
令 ,得
∴函数 的单调递增区间为 ……………………………6分
(2)
令 ( ),
则
可得,当 即 时, ;
高三数学试卷 共6页 第3页
学科网(北京)股份有限公司当 即 时,
∵存在 , ,对任意 ,
有 恒成立,
∴ 为 的最小值, 为 的最大值,
∴ , ,
∴ ,
∴ . ……………………………12分
22.【答案】(1) (2)见解析
【解析】
【分析】(1)转化为 有两个根,讨论单调性结合函数图象可求解;(2)等价于证明
构造函数即可证明.
【小问1详解】
由题可知, ,令 ,即 ,即 有两个根 ,
令 ,则 ,
由 得, ,解得 ;由 得, ,解得 ,
所以 在 单调递增, 单调递减, 时 ,
所以要使 有两个根,则 ,
解得 ,所以 . ……………………………12分
【小问2详解】
由(1)可知 且 ,所以
要证 ,只用证 ,等价于证明 ,
而 ,即 ,故等价于证明 ,
即证 .令 ,则 ,于 等价于证明 成立,
是
高三数学试卷 共6页 第4页
学科网(北京)股份有限公司设 , ,
所以 在 上单调递增,
故 ,即 成立,
所以 ,结论得证. ……………………………12分
高三数学试卷 共6页 第5页
学科网(北京)股份有限公司高三数学试卷 共6页 第6页
学科网(北京)股份有限公司