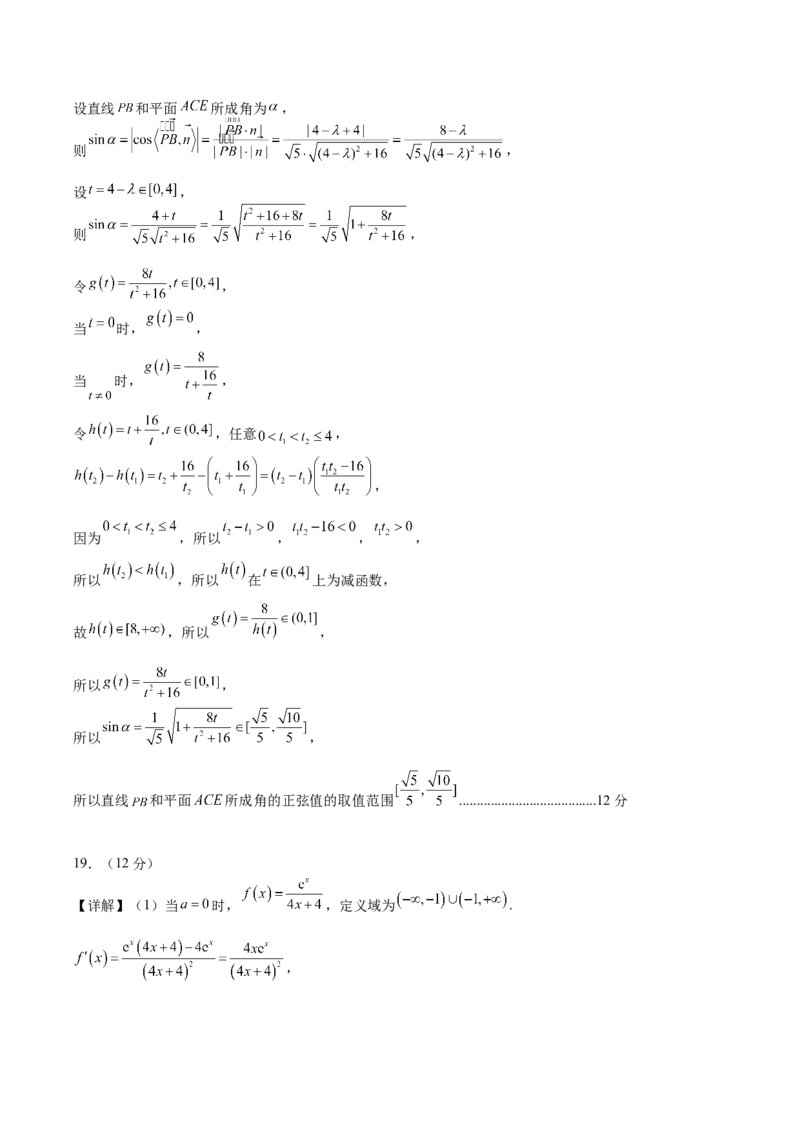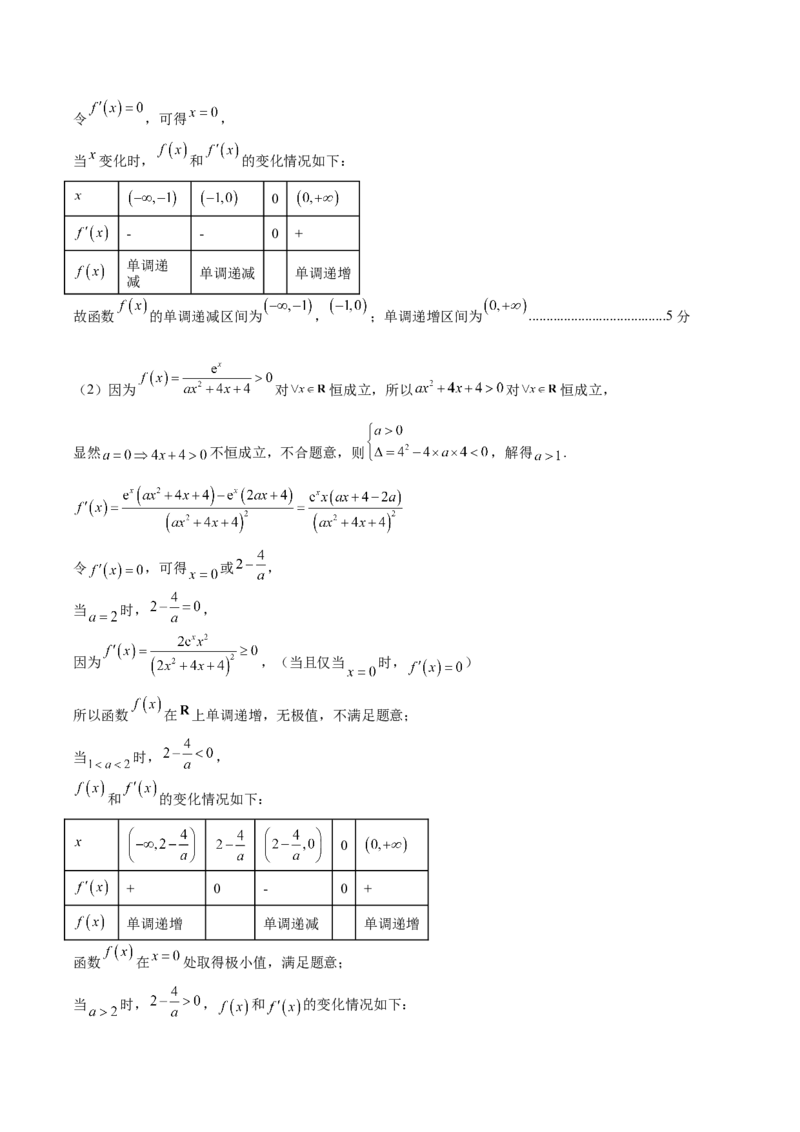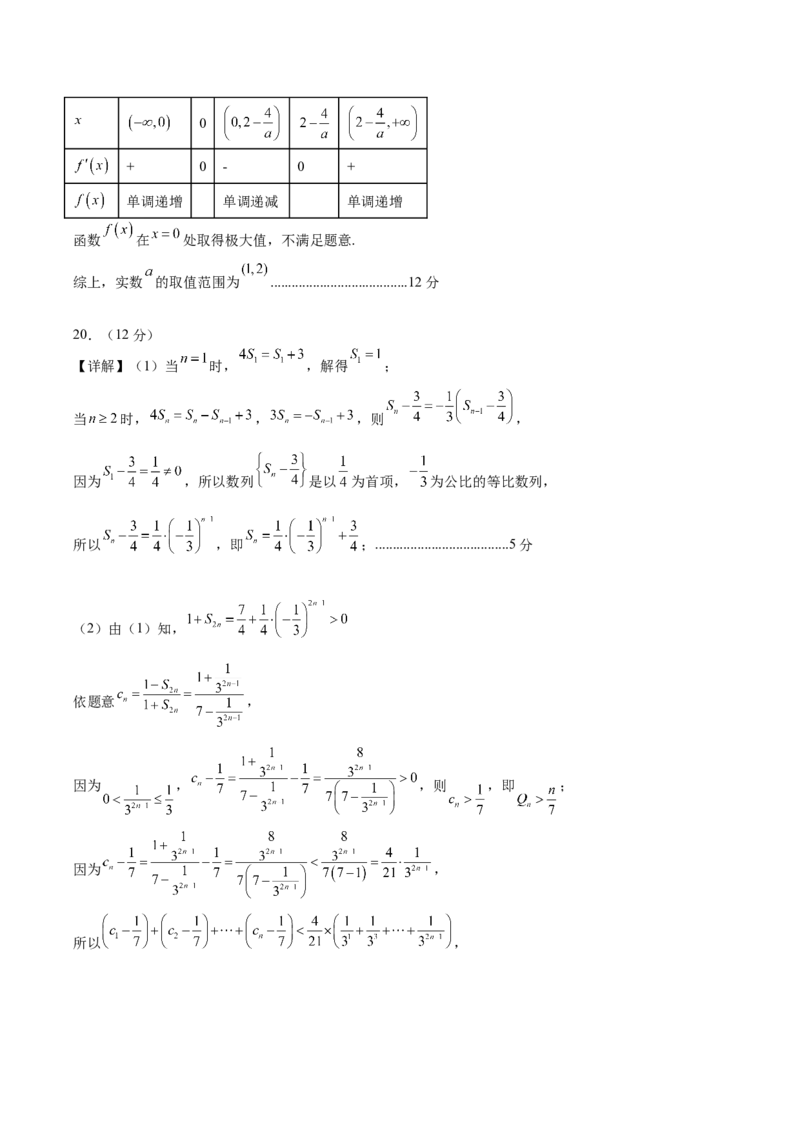文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考Ⅰ卷专用)
黄金卷·参考答案
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1 2 3 4 5 6 7 8
A D C C B C B A
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9 10 11 12
BD ACD BC BC
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.32 14. 16. 16.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)
【详解】(1)设 的边长为 千米,由 得 ,
中,
为等边三角形, ,
故 ,即 的边长为 .......................................5分
(2)设 的边长为 千米,所以 ,
中, ,
由正弦定理得, ,故 ,其中 ,当 时, 取得最小值 ,
即 的边长最小值为 .......................................10分
18.(12分)
【详解】(1)在正方形 中 ,
∵面 面 面 ,面 面 ,
∴ 面 ,
∵ 面 ,∴ ,
∵ 在以 为直径的半圆上,∴ ,
又∵ 面 , 面 ,
又 面 ,
∴面 面 ,......................................5分
(2)∵ ,∴
又∵ 为二面角 的平面角,
∴ ,同理 .
在梯形 中, .
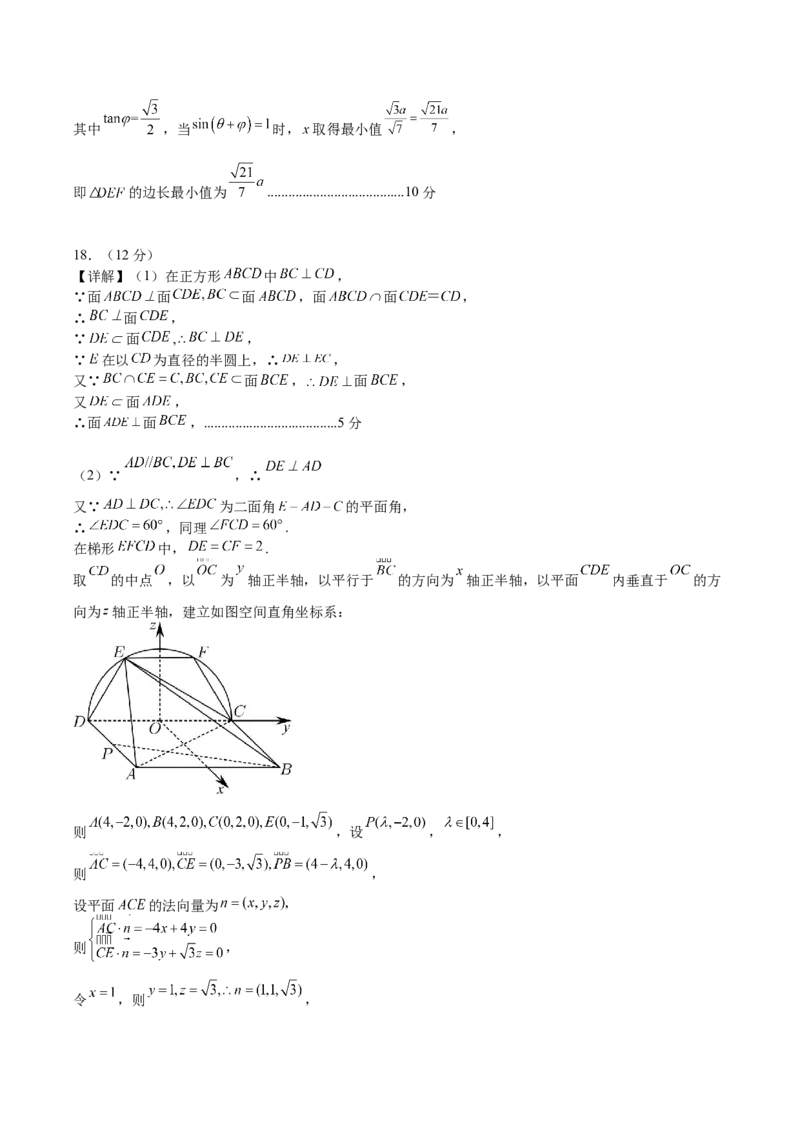
取 的中点 ,以 为 轴正半轴,以平行于 的方向为 轴正半轴,以平面 内垂直于 的方
向为 轴正半轴,建立如图空间直角坐标系:
则 ,设 , ,
则 ,
设平面 的法向量为
则 ,
令 ,则 ,设直线 和平面 所成角为 ,
则 ,
设 ,
则 ,
令 ,
当 时, ,
当 时, ,
令 ,任意 ,
,
因为 ,所以 , , ,
所以 ,所以 在 上为减函数,
故 ,所以 ,
所以 ,
所以 ,
所以直线 和平面 所成角的正弦值的取值范围 .......................................12分
19.(12分)
【详解】(1)当 时, ,定义域为 .
,令 ,可得 ,
当 变化时, 和 的变化情况如下:
0
- - 0 +
单调递
单调递减 单调递增
减
故函数 的单调递减区间为 , ;单调递增区间为 .......................................5分
(2)因为 对 恒成立,所以 对 恒成立,
显然 不恒成立,不合题意,则 ,解得 .
令 ,可得 或 ,
当 时, ,
因为 ,(当且仅当 时, )
所以函数 在 上单调递增,无极值,不满足题意;
当 时, ,
和 的变化情况如下:
0
+ 0 - 0 +
单调递增 单调递减 单调递增
函数 在 处取得极小值,满足题意;
当 时, , 和 的变化情况如下:0
+ 0 - 0 +
单调递增 单调递减 单调递增
函数 在 处取得极大值,不满足题意.
综上,实数 的取值范围为 .......................................12分
20.(12分)
【详解】(1)当 时, ,解得 ;
当 时, , ,则 ,
因为 ,所以数列 是以 为首项, 为公比的等比数列,
所以 ,即 ;......................................5分
(2)由(1)知,
依题意 ,
因为 , ,则 ,即 ;
因为 ,
所以 ,而 ,
故 ,即 .
综上所述, .......................................12分
【点睛】关键点睛:本题第二问考查数列,不等式,放缩法的综合应用问题,第二问的难点是证明
,关键是证明 ,后面的问题迎刃而解.
21.(12分)
【详解】(1) , , ;......................................3分
(2)由已知 ,∴ ,即 ,
∴ 是以 为公比的等比数列,
∴ ,∴ .......................................7分
(3) .
设 , ,∴ ,∴ 在 上单调递增,
显然 ,则 ,
∴ ,则 ,
即 ,
∴ .......................................12分
22.(12分)【详解】(1)设 ,由题意可得 ,即 ,
解得 或 (舍去),所以抛物线 的方程为 .......................................5分
(2)如图,
设经过 , 两点的直线方程为 : ( ),
与抛物线方程 联立可得 ,
即 ,
∴ , .
∵ ,则 ,
∴ ,
∴过点 作 的切线 方程为 ,
令 ,得 ,即 .
同理,过点 作 的切线 方程为 ,
令 ,得 ,即 .
∴ .
联立两直线方程 ,解得 ,即 ,......................................8分则 到直线 的距离 .
又∵过点 作直线 垂直于 ,
直线 的方程为 ,
令 ,得 ,即 .
同理,直线 的方程为 ,
令 ,得 ,即 .
∴ .
联立两直线方程 ,解得 ,
整理后可得 ,即 ,......................................10分
则 到直线 的距离 .
由上可得 , ,
, ,
∴ ,得 ,
∴直线 的方程为 即 .......................................12分