文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考II 卷专用)
黄金卷
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.已知集合 ,则 ( )
A. B. C. D.
【答案】B
【详解】 ,
又 ,则 .
故选:B.
2. ( )
A. B.
C. D.
【答案】A
【详解】 .
故选:A
3.斜拉桥是将梁用若干根斜拉索拉在塔柱上的桥,它由梁、斜拉索和塔柱三部分组成.如图1,这是一座
斜拉索大桥,共有10对永久拉索,在索塔两侧对称排列.如图2,已知拉索上端相邻两个锚的间距
约为4m,拉索下端相邻两个锚的间距 均为18m.最短拉索的锚 ,
满足 , ,以 所在直线为 轴, 所在直线为 轴,则最长拉索所在直线的
斜率为( )A. B. C. D.
【答案】B
【详解】由题意知 , 分别是公差为4和18的等差数列,
所以 , ,
所以 , ,即最长拉索所在直线的斜率为 .
故选:B.
4.已知平面向量 , , ,若 ,则 ( )
A. B.5 C.2 D.
【答案】D
【详解】 ,
,
因为 ,所以 ,
所以 ,解得 .
故选:D5.2023年杭州亚运会期间,甲、乙、丙3名运动员与5名志愿者站成一排拍照留念,若甲与乙相邻、丙
不排在两端,则不同的排法种数有( )
A.1120 B.7200 C.8640 D.14400
【答案】B
【详解】甲与乙相邻有 种不同的排法,将甲与乙看作是一个整体,与除丙外的5人排好,有 种不同
的排法,
再将丙排入隔开的不在两端的5个空中,有 种不同的排法,
所以共有 种不同的排法.
故选:B.
6.已知角 ,且 , ,则 ( )
A. B. C. D.2
【答案】C
【详解】因为 ,
所以 ,
所以 ,
则 ,
又 ,则 ,
则 ,
所以 .
故选:C.
7.已知正三棱锥 的外接球的表面积为 ,若 平面PBC,则三棱锥 的体积为
( )A. B. C. D.
【答案】A
【详解】设外接球半径为 ,则 ,所以 .
设 ,因为 平面PBC,所以 ,
所以 ,又因为△ABC为正三角形, ,
即PA,PB,PC两两垂直.
将三棱锥补成以PA,PB,PC为邻边的正方体,则 ,得 ,
所以三棱锥的体积为 .
故选:A.
8.函数 和 的定义域均为 ,已知 为偶函数, 为奇函数,对于 ,
均有 ,则 ( )
A.66 B.70 C.124 D.144
【答案】B
【详解】 为偶函数,即 ,
的图像关于 对称,
为奇函数,即 ,
的图像关于点 对称,
对于 ,均有 ,
,
的图像关于 对称, ,的图像关于点 对称,
又
解得 ,
.
故选:B.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.对于函数 ,有以下四种说法正确的是:( )
A.函数的最小值是
B.图象的对称轴是直线
C.图象的振幅为2,初相为
D.函数在区间 上单调递增
【答案】AD
【详解】因为函数 ,则有:
对于选项A:当 ,即 时,
函数 取得最小值为 ,故A正确;
对于选项B:令 ,解得 ,
函数 的图象的对称轴是直线 ,故B错误;对于选项C:因为 ,
所以图象的振幅为2,
令 ,解得 ,
所以 不为初相,故C错误;
对于选项D:令 ,解得 ,
即函数 的递增区间为 ,
当 时, 的递增区间为 ,故D正确.
故选:AD.
10.(多选题)“堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》:
“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.一个长方体沿对角面斜解(图1),得到
一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得一个四棱锥称为阳马
(图3),一个三棱锥称为鳖臑(图4).若长方体的体积为V,由该长方体斜解所得到的堑堵、阳马和鳖
臑的体积分别为 , , ,则下列选项正确的是( )
A. B. C. D.
【答案】ACD
【详解】设长方体的长宽高分别为 , ,
则 , , ,
故 , , , ,则B错误,ACD正确;
故选:ACD.11.已知 为坐标原点,点 在抛物线 上,过点 的直线交抛物线 于
两点,则下列结论正确的是( )
A.抛物线 的准线方程为 B.直线 与抛物线 相切
C. 为定值 D.
【答案】ABD
【分析】选项A,由点 在抛物线上,代入方程待定系数,求出抛物线C方程,则得到准线方程;
选项B,利用导数求出切线斜率,与直线 斜率相同即可说明相切;选项C,设出直线AB方程,联立抛
物线方程,将 坐标化韦达定理代入可证;选项D,利用弦长公式用 表示,再代入韦达
定理,结合判别式 得出的 的范围,即可判断得出答案.
【详解】对于A:因为点 在抛物线 : 上,
则 ,解得 ,
所以抛物线 : ,
其准线为 ,故A正确;
对于B:令 ,
则 ,可得 ,
即抛物线在A点处切线斜率与直线AB斜率相同,
所以直线AB与抛物线C相切,故B正确;
对于C:由题意可知,直线PQ斜率存在,
设直线PQ的方程为 ,联立方程 ,消去y得: ,
可得 ,得 ,
且 ,
因为
,故C错误;
对于D:由题意可知 ,
因为 ,
则 ,
所以 ,故D正确.
故选:ABD.
12.若实数x,y满足 ,则( )
A. B.
C. D.
【答案】AD【分析】对于AB, ,则 ,从而可求出 的范
围进行判断,对于C,利用 ,化简变形结合已知条件可判断,对于D,利用 ,
化简变形结合已知条件可判断.
【详解】对于AB,因为 ,所以 ,当且仅当 时
取等号,
所以 ,所以 ,所以A正确,B错误,
对于C,因为 ,所以 ,当且仅当 时取等号,
所以 ,所以 ,
所以 ,
所以 ,当且仅当 时取等号,所以C错误,
对于D,因为 ,所以 ,当且仅当 时取等号,
所以 ,所以 ,
所以 ,当且仅当 时取等号,所以D正确,
故选:AD
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知随机变量 服从正态分布 ,且 ,则 .
【答案】 /
【详解】随机变量 服从正态分布 ,且 ,所以 ,
所以 ,
故答案为:
14.已知函数 ,过原点作曲线 的切线 ,则切线 的斜率为 .
【答案】
【详解】由题意得, ,设切点为 ,
则切线方程为 ,
因为切线过原点,
所以 ,
解得 ,所以 .
故答案为:
15.已知圆C: ,直线 ,若在l上总存在点M,使得
过M点作的圆C的两条切线互相垂直,则实数m的取值范围是 .
【答案】
【详解】根据题意,圆C: 即 ,
其圆心为 ,半径 ,
如图,设切点分别为A, 连接AC,BC,MC,
由 ,又由 ,
则四边形MACB为正方形且 ,
若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心 到直线l的距离 ,
即 ,
解可得: ,
即m的取值范围为 ;
故答案为:
16.已知椭圆 : 的左,右焦点分别为 , ,过点 且垂直于 轴的直线与椭圆交
于 、 两点, 、 分别交 轴于 、 两点, 的周长为4.过 作 外角平分线的垂线
与直线 交于点 ,则 .
【答案】
【详解】因为 ,所以 ,
因为 的周长为4,所以 的周长 ,
所以 ,所以椭圆方程为 , ,所以 ,
直线 垂直 轴,设 ,代入 ,求得 ,所以 , ,
因为 外角平分线 的垂线与直线 交于点 ,
所以 ,可得 ,
则 ,所以 .
故答案为: .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.已知数列 为等差数列, 是公比为 的等比数列,且 .
(1)证明: ;
(2)若集合 ,求集合 中的元素个数.
【答案】(1)证明见解析
(2)6
【详解】(1)证明:设数列 的公差为 ,则 ,
即 ,
解得 ,所以原命题得证.
(2)由(1)知 ,所以 ,因为 ,所以 ,解得 ,
由 , ,故 ,即 ,
所以满足等式的解 .
故集合 中的元素个数为6.
18.在① ;② 这两个条件中任选一个,补充在下面问题中并解答.
问题:设 的内角 , , 的对边分别为 , , ,且 , ,______.
(1)求 ;
(2)求 的周长.
注:若选择条件①、条件②分别解答,则按第一个解答计分.
【答案】(1)
(2)
【详解】(1)在 中, ,
,
,
,
则 ,
化简得 .
在 中, ,
.
又 ,
.
(2)由余弦定理,得 ,即 .
若选①,,即 ,且 ,
, ,
此时 的周长为 .
若选②,
,
,即 ,
又 ,
,
此时 的周长为 .
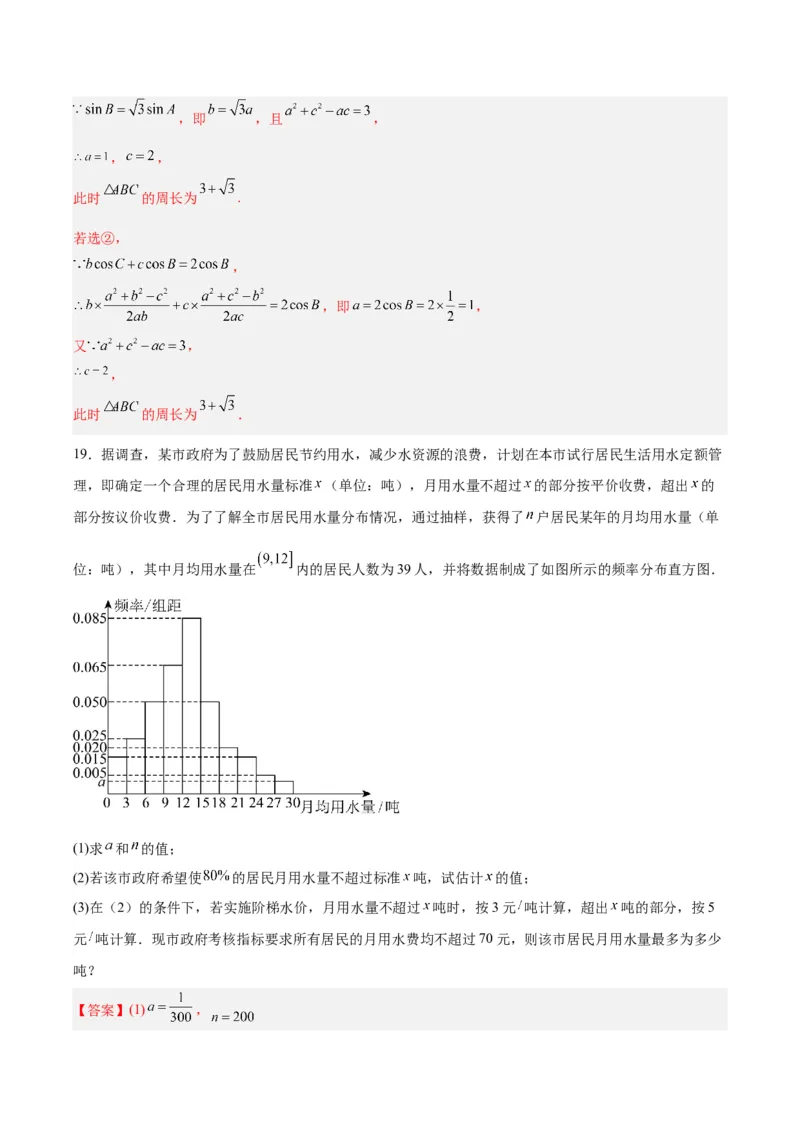
19.据调查,某市政府为了鼓励居民节约用水,减少水资源的浪费,计划在本市试行居民生活用水定额管
理,即确定一个合理的居民用水量标准 (单位:吨),月用水量不超过 的部分按平价收费,超出 的
部分按议价收费.为了了解全市居民用水量分布情况,通过抽样,获得了 户居民某年的月均用水量(单
位:吨),其中月均用水量在 内的居民人数为39人,并将数据制成了如图所示的频率分布直方图.
(1)求 和 的值;
(2)若该市政府希望使 的居民月用水量不超过标准 吨,试估计 的值;
(3)在(2)的条件下,若实施阶梯水价,月用水量不超过 吨时,按3元 吨计算,超出 吨的部分,按5
元 吨计算.现市政府考核指标要求所有居民的月用水费均不超过70元,则该市居民月用水量最多为多少
吨?
【答案】(1) ,(2)16.6吨
(3)20.64吨
【详解】(1) ,
用水量在 的频率为 , (户)
(2) ,
,
(吨)
(3)设该市居民月用水量最多为 吨,因为 ,所以 ,
则 ,解得 ,
答:该市居民月用水量最多为20.64吨.
20.如图,在四棱锥 中,底面ABCD是正方形, 底面ABCD,E,F分别是PC,AD中点.
(1)求证: 平面 ;
(2)若 ,PB与平面ABCD所成角为45°,求平面PFB与平面EFD夹角的余弦值.
【答案】(1)证明见解析
(2)
【详解】(1)设 为 中点,连接 ,
又 分别是 中点,所以 , ,
又底面 是正方形,
所以 , ,故四边形 为平行四边形,则 ,
由 平面 , 平面 ,则 平面 .
(2)因为PB与平面ABCD所成角为45°,所以 ,以 为原点,构建空间直角坐标系,
由于 ,则 ,
所以 ,
所以 ,
令 为平面 的一个法向量,则 ,
令 ,即 ,
令 为平面 的一个法向量,则 ,
令 ,即 ,所以 ,
即平面 与平面 夹角的余弦值 .
21.已知双曲线 : 经过点 ,且浙近线方程为 .
(1)求 的方程;
(2)过点 作 轴的垂线,交直线 : 于点 ,交 轴于点 .不过点 的直线交双曲线 于A、B两
点,直线 , 的斜率分别为 , ,若 ,求 .
【答案】(1) ;
(2)
【详解】(1)由 ,即 ,
将 代入双曲线方程得 ;
(2)
当直线 的斜率存在时,不妨设直线 , ,
联立双曲线方程 ,其中 ,
,
易知
,
化简得
所以 或 ,
当 时,直线 过P,不符题意舍去,
故 ,则此时直线 ,过定点 .
如图所示,易知 ,
则 ;
当直线 的斜率不存在时,可设 ,
与双曲线方程联立,则 ,
可令 ,
此时 ,
此时 重合,不符题意舍去.
综上可知 .
【点睛】关键点睛:本题关键点在于第二问中由条件转化 中 的关系,此外三角形面积比
转化为线段比也是简化计算的关键.22.已知函数 .
(1)当 时,求 的极值;
(2)若 ,求 的值;
(3)求证: .
【答案】(1) 在 处取得极小值 ,无极大值
(2)
(3)证明见解析
【详解】(1)当 时, , ,
则 ,
当 时, , 单调递减,
当 时, , 单调递增,
所以 在 处取得极小值 ,无极大值;
(2)由题意得 ,
①当 时, ,所以 在 上单调递增,
所以当 时, ,与 矛盾;
②当 时,当 时, , 单调递减,
当 时, , 单调递增,
所以 ,因为 恒成立,所以 ,
记 , ,
当 时, , 单调递增,
当 时, , 单调递减,
所以 ,所以 ,
又 ,
所以 ,
所以 ;
(3)证明:先证 ,
设 ,则 ,
所以 在区间 上单调递减,
所以 ,即 ,
所以 ,
再证 ,
由(2)可知 ,当 时等号成立,
令 ,则 ,
即 ,
所以 , , ,累加可得 ,
所以 .
【点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成
立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极
(最)值问题处理.