文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考II 卷专用)
黄金卷
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.设全集 ,集合 , ,则 ( ).
A. B. C. D.
【答案】C
【分析】先化简集合集合 ,从而利用集合交并补运算即可得解.
【详解】因为 ,
又 ,所以 ,
因为 ,
所以 ,
故选:C
2.已知复数z满足 ,则 ( )
A.2 B.3 C.4 D.
【答案】D
【分析】先根据复数的四则运算化简复数,再计算模长即可.
【详解】复数 ,有
故选:D3.已知向量 , ,且 与 方向相反,若 ,则 在 方向上的投影向量的坐标
是( )
A. B. C. D.
【答案】B
【分析】根据向量的共线求得m的值,结合 与 方向相反确定m,根据向量的投影向量的定义即可求得
答案.
【详解】由题意知向量 , 共线,
故 ,解得 或 ,
又因为且 与 方向相反,故 ,
所以 ,而 ,
则 在 方向上的投影向量是 ,
即 在 方向上的投影向量的坐标是 ,
故选:B
4.按从小到大顺序排列的两组数据:甲组:27,31,37,m,42,49;乙组:24,n,33,44,48,52,
若这两组数据的第30百分位数、第50百分位数都分别对应相等,则 ( )
A.60 B.65 C.70 D.71
【答案】D
【分析】利用百分位数的定义即可得解.
【详解】因为甲组:27,31,37,m,42,49;乙组:24,n,33,44,48,52,
由 ,得第30百分位数是第2个数据,故 ,
由 ,得第50百分位数是第3与4个数据平均值 ,解得 .
所以 .故选:D.
5.已知 , , .若 , ,则 ( )
A. B. C. D.
【答案】B
【分析】根据题意分析可得 ,利用两角和差公式结合指数幂运算求解.
【详解】由题意可得 ,
因为 , ,则 ,
可得 ,即 ,
则 ,
令 ,
则 ,整理得 ,解得 或 (舍去),
即 ,解得 .
故选:B.
6.定义在R上的奇函数 ,对任意 都有 ,若 ,则不等式
的解集是( )
A. B.
C. D.
【答案】C
【分析】构造 ,确 在 上单调递减, 为奇函数,得到 ,解得答案.【详解】 , ,则 ,
设 ,故 , 在 上单调递减,
为奇函数,则 , 为奇函数,
在 上单调递减, , ,
,即 ,故 ,
故选:C.
7.古希腊数学家阿波罗尼奥斯所著的八册《圆锥曲线论(Conics)》中,首次提出了圆锥曲线的光学性质,
其中之一的内容为:“若点 为椭圆上的一点, 、 为椭圆的两个焦点,则点 处的切线平分
外角”.根据此信息回答下列问题:已知椭圆 , 为坐标原点, 是点 处的切线,过
左焦点 作 的垂线,垂足为 ,则 为( )
A. B. C. D.
【答案】A
【分析】延长 、 交于点 ,分析可知,则 为 的中点,且 ,利用中位线的性质结
合椭圆的的定义可求得 的值.
【详解】如下图所示:延长 、 交于点 ,由题意可知 ,
又因为 ,则 为 的中点,且 ,
所以, ,
又因为 为 的中点,则 .
故选:A.
8.已知点 在棱长为2的正方体表面上运动, 是该正方体外接球的一条直径,则 的最小值为
( )
A.-2 B.-8 C.-1 D.0
【答案】A
【分析】通过基底法,得到 ,再通过立体图得到 的值以及 的最小值,最终代
入数据得到最小值.
【详解】如图 为棱长为2的正方体外接球的一条直径, 为球心, 为正方体表面上的任一点,
则球心 也就是正方体的中心,
所以正方体的中心 到正方体表面任一点 的距离的最小值为正方体的内切球的半径,它等于棱长的一半,即长度为1, 的长为正方体的对角线长,为 ,
我们将三角形 单独抽取出来如下图所示:
,所以 的最小值为 .
故选:A.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知函数 的部分图象如图所示,下列说法正确的是( )
A.
B.函数 的图象关于 对称
C.函数 在 的值域为
D.要得到函数 的图象,只需将函数 的图象向左平移 个单位
【答案】ACD【分析】先由图象信息求出 表达式,从而即可判断A;注意到 是 的对称
中心当且仅当 ,由此即可判断B;直接由换元法结合函数单调性求值域对比即
可判断C;直接按题述方式平移函数图象,求出新的函数解析式,对比即可判断.
【详解】如图所示:
由图可知 ,又 ,
所以 ,所以 ,
又函数图象最高点为 ,
所以 ,即 ,
所以 ,解得 ,
由题意 ,所以只能 ,故A选项正确;
由A选项分析可知 ,而 是 的对称中心当且仅当
,但 ,从而函数 的图象不关于 对称,故B选项错误;
当 时, , ,
而函数 在 上单调递减,在 上单调递增,
所以当 时, ,
所以函数 在 的值域为 ,故C选项正确;
若将函数 的图象向左平移 个单位,
则得到的新的函数解析式为 ,故
D选项正确.
故选:ACD.
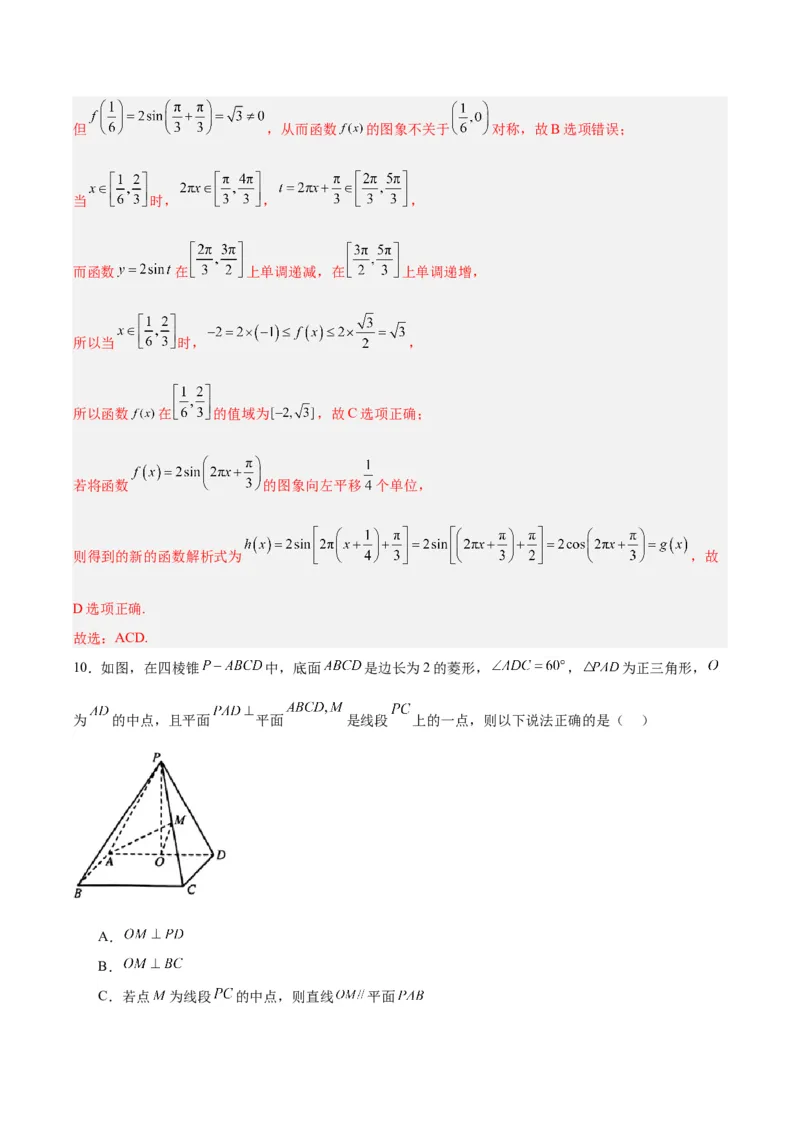
10.如图,在四棱锥 中,底面 是边长为2的菱形, , 为正三角形,
为 的中点,且平面 平面 是线段 上的一点,则以下说法正确的是( )
A.
B.
C.若点 为线段 的中点,则直线 平面D.若 ,则直线 与平面 所成角的余弦值为
【答案】BCD
【分析】根据题意,由线面垂直的判断定理即可判断AB,由线面平行的判定定理即可判断C,建立空间
直角坐标系,结合空间向量的坐标运算,即可判断D.
【详解】连接 ,
因为底面 是边长为2的菱形, ,又 为正三角形, 为 的中点,所以 ,
,又 , 平面 ,所以 平面 ,又 平面 ,所以
,又 ,所以 ,故B正确;
当点 为线段 的中点时,取 的中点 ,连接 ,则 ,且 ,又 为 的
中点,底面 是边长为 的菱形,所以 ,且 ,所以 ,且 ,所以
四边形 为平行四边形,所以 ,又 平面 , 平面 ,所以 平面 ,
故C正确;
因为平面 平面 , 为正三角形, 为 中点,所以 ,平面 平面
, 平面 ,所以 平面 ,且 平面 ,所以 ,又
, , 平面 ,所以 平面 ,又 平面 ,所以
,显然 与平面 不垂直,故当点 运动到点 位置时,才有 ,故A错误;
建立如图所示的空间直角坐标系,则 ,
又 ,所以 ,则 , , ,设平面的法向量为 ,则 ,令 ,则 ,所以 ,设
直线 与平面 的夹角为 ,则 ,则
,所以直线 与平面 所成角的余弦值为 ,故D正确;
故选:BCD
11.下列式子中最小值为4的是( )
A. B.
C. D.
【答案】BC
【分析】对于ABC:利用基本不等式运算求解;对于D:取特值 代入检验.
【详解】对于选项A:因为 ,则 ,
当且仅当 ,即 时等号成立,
但 ,所以 的最小值不为4,故A错误;
对于选项B:因为 ,则 ,
当且仅当 ,即 时,等号成立,
所以 的最小值为4,故B正确;
对于选项C:因为 ,
则 ,当且仅当 ,即 时,等号成立,故C成立;
对于选项D:令 ,可得 ,
所以4不是 的最小值,故D错误;
故选:BC.
12.已知拋物线 ,过其准线上的点 作 的两条切线,切点分别为 ,则下
列说法正确的是( )
A.抛物线 的方程为 B.
C.直线 的斜率为 D.直线 的方程为
【答案】BCD
【分析】由准线所过点求得 得抛物线方程,判断A,设直线 ,代入抛物线方程后应用韦达
定理判断B,设 , ,利用选项B中斜率 表示出 两点坐标,计算斜率判断C,利
用韦达定理得出线段 中点坐标得直线方程判断D.
【详解】因为 在准线上,所以准线方程为 ,所以 ,抛物线 的方程为 ,故A
错误;
设直线 ,代入 ,得 ,
当直线与 相切时, ,即 ,
设 的斜率分别为 ,易知 是上述方程的两根,故 ,
所以 ,故B正确;
设 , ,则 分别是方程 的根,
所以 ,所以 ,故C正确;, ,
所以 的中点为 ,直线 的方程为 ,即 ,故D正确.
故选:BCD.
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知幂函数 在区间 上单调递减,则 .
【答案】
【分析】利用幂函数的定义及单调性求解即得.
【详解】由幂函数的定义知, ,即 ,解得 或 ,
当 时, 在区间 上单调递增,不符合题意,
当 时, 在区间 上单调递减,符合题意,所以 .
故答案为:
14.已知圆M的圆心在直线 上,且过 , ,则圆M的方程为 .
【答案】
【分析】根据圆M的圆心在直线 上,设圆心为 ,再根据圆过点 , ,由
求解.
【详解】解:因为圆M的圆心在直线 上,且过 , ,
所以设圆心为 , ,
解得 ,则圆心为 , ,
所以圆的方程为: ,故答案为:
15.已知二项式 的展开式中只有第4项的二项式系数最大,现从展开式中任取2项,
则取到的项都是有理项的概率为 .
【答案】
【分析】根据题意得到展开式的总项数为7项, ,然后利用展开式的通项公式得到有理项项数,再利
用古典概型的概率求解.
【详解】因为二项式的展开式中只有第4项的二项式系数最大,
所以展开式的总项数为7项,故 ,
展开式的通项 ,
当 是偶数时该项为有理项,
时,项为有理项,共有4项,
所以所有项中任取2项,都是有理项的概率为 .
故答案为:
16.已知函数 ,若关于 的方程 恰有 个不同实数根,则实
数 的取值范围为 .
【答案】
【分析】先利用导数研究 时 的性质,作出 的图象.若关于 的方程
恰有 个不同实数根,令 ,通过分析可得 有2个
不等实根 ,且 ,数形结合即可建立关于 的不等式组,即可求解.【详解】当 时, ,则 ,
令 ,解得 ,
所以当 时, , 单调递增,
当 时, , 单调递减,
根据题意可作出 的图象如下:
若关于 的方程 恰有4个不同实数根,
令 , ,则 有两个不等实数根 ,
故 与 都有2个交点,或者 与 有1个交点, 与 有3个交点;
当 与 都有2个交点,根据图象可得 ,不满足 ,舍去;
当 与 有1个交点, 与 有3个交点,
则 ,当 时, ,解得 ,
故 ,解得 或 ,舍去;
故 ,
两个实数根的范围为 ,
所以 ,解得 ,所以实数 的取值范围为 .
故答案为: .
【点睛】关键点睛:本题求解的关键是利用数形结合思想,作出函数的图象,通过图象得到 与
有1个交点, 与 有3个交点,并通过分析得到 .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.记数列 的前n项和为 ,对任意正整数n,有 ,且 .
(1)求数列 的通项公式;
(2)设 ,数列 的前n项和为 ,求证: .
【答案】(1)
(2)证明见解析
【分析】(1)根据数列递推式 ,利用 可得 ,利用累乘法,结合验
证首项,即可求得答案;
(2)由(1)可得 的表达式,利用错位相减法可求得 ,即可证明结论.
【详解】(1)由题意对任意正整数n,有 ,
则 时, ,即 ;
当 时, ,则 ,
即 ,即 ,故 时, ,
也适合上式,故 ;
(2)证明:由(1)可得 ,
故 ,
则 ,
故
,
故 ,由于 ,故 ,
故 .
18.在 中,角A,B,C所对的边分别为a,b,c,已知
(1)求角 ;
(2) 是 的角平分线,若 , ,求 的面积.
【答案】(1) ;
(2) .
【分析】(1)由正弦边角关系及已知得 ,即可得角 ;
(2)由余弦定理得 ,由 及面积公式得 ,求得 ,进而应用面积公式求面积.
【详解】(1)由 ,得: ,即 ,
又 ,所以 .
(2)在 中, 得: ①,又 ,
得: ,化简得: ②,
由①②得: ,所以
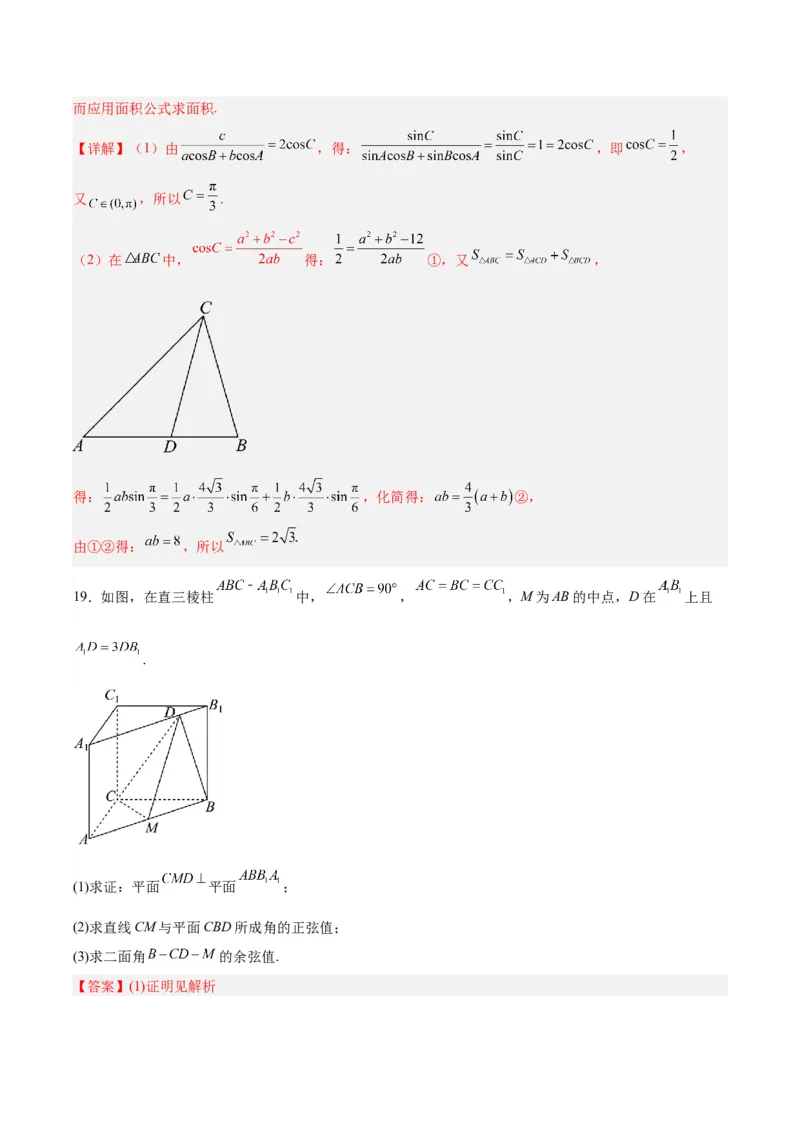
19.如图,在直三棱柱 中, , ,M为AB的中点,D在 上且
.
(1)求证:平面 平面 ;
(2)求直线CM与平面CBD所成角的正弦值;
(3)求二面角 的余弦值.
【答案】(1)证明见解析(2)
(3)
【分析】(1)证明 ,推出 平面 ,进而可得结论;
(2)以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,利用向量法求直线CM与
平面CBD所成角的正弦值;
(3)利用向量法求二面角 的余弦值.
【详解】(1) 直三棱柱 中, ,M为AB的中点,
, 平面 , 平面
,又 , 平面 ,
平面 ,又 平面 ,
平面 平面 ;
(2)以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
设 ,
则 ,
设面 的法向量 ,
则 ,取 ,得 ,
设直线CM与平面CBD所成角为 ,;
(3)设面 的法向量为 ,又 ,
,取 得 ,
,
所以二面角 的余弦值为 .
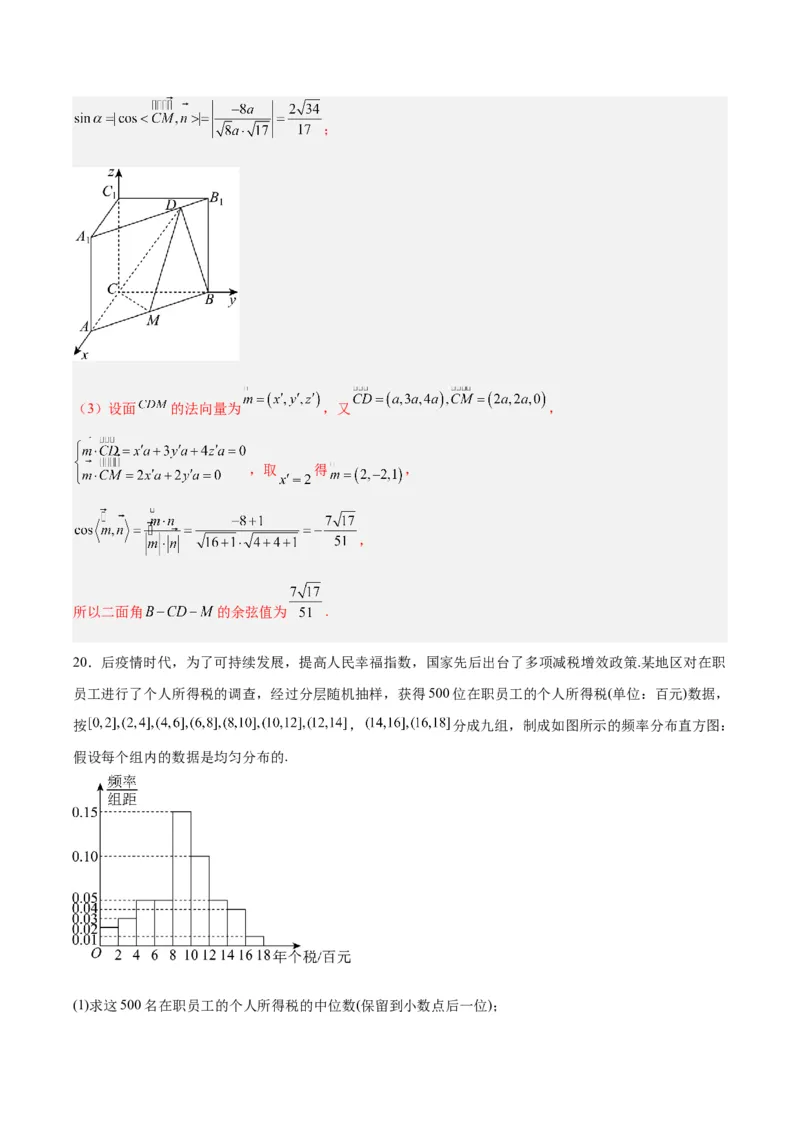
20.后疫情时代,为了可持续发展,提高人民幸福指数,国家先后出台了多项减税增效政策.某地区对在职
员工进行了个人所得税的调查,经过分层随机抽样,获得500位在职员工的个人所得税(单位:百元)数据,
按 , 分成九组,制成如图所示的频率分布直方图:
假设每个组内的数据是均匀分布的.
(1)求这500名在职员工的个人所得税的中位数(保留到小数点后一位);(2)从个人所得税在 三组内的在职员工中,采用分层抽样的方法抽取了10人,现从这10
人中随机抽取3人,记年个税在 内的员工人数为 ,求 的分布列和数学期望;
(3)以样本的频率估计概率,从该地区所有在职员工中随机抽取100名员工,记年个税在 内的员工人
数为 ,求 的数学期望与方差.
【答案】(1) 百元
(2)分布列见解析,
(3)
【分析】(1)根据频率分布直方图的性质求得 ,利用中位数计算公式计算即可.
(2)求得 的所有可能取值和对应的概率即可得到分布列,再由数学期望公式计算即可.
(3)由题意得 ,由二项分布的数学期望与方差公式直接计算即可.
【详解】(1)设这500名在职员工的个人所得税的中位数为 ,
则由频率分布直方图得 ,
解得 ,
所以这500名在职员工的个人所得税的中位数为 百元.
(2)由题意抽取的10人中,年个税在 内的员工人数为 人,
年个税在 内的员工人数为 人,
年个税在 内的员工人数为 人,
若现从这10人中随机抽取3人,记年个税在 内的员工人数为 ,
则 的所有可能取值为 ,
所以 , ,, ,
所以 的分布列为:
0 1 2 3
的数学期望为: .
(3)由频率分布直方图可知年个税在 内的概率为 ,
从该地区所有在职员工中随机抽取100名员工,恰有 个员工的年个税在 内的分
布列服从二项分布 ,
由二项分布的数学期望、方差公式可得 ,
即 的数学期望与方差分别为 .
21.在 中,已知点 边上的中线长与 边上的中线长之和为 ,记
的重心G的轨迹为曲线C.
(1)求C的方程;
(2)若圆 ,过坐标原点O且与y轴不重合的任意直线 与圆 相交于点 ,直线
与曲线 的另一个交点分别是点 ,求 面积的最大值.
【答案】(1)
(2)
【分析】(1)根据椭圆的定义求得曲线 的方程.(2)直线 为 ,通过联立方程组等求得 两点的坐标,求得 面积的表达式,利用换
元法以及函数的单调性求得 面积的最大值.
【详解】(1)设 的中点为S, 的中点为T,所以 , ,
所以 ,所以 ,
所以G点的轨迹是以 为焦点,长轴长 的椭圆.所以 ,
所以 , ,所以曲线C的方程为 .
.
(2)设直线 为 (不妨设 ),设 , ,
所以 , , ,
解得 ( 舍去),则 ,
由于AB是单位圆的直径,所以 ,
所以直线EN的斜率为 ,直线EN的方程为 ,
同理可求得 ,则 ,由上述分析可知 , ,而 ,
所以
,
所以 ,令 ,
当且仅当 , 时等号成立,
则 ,函数 在 上单调递增,
所以当 时, 取得最小值为 .
【点睛】关键点睛:在圆锥曲线中,求解三角形面积最值、范围等的有关问题,关键点有两点,第一点是
求得三角形面积的表达式,可考虑根与系数关系、点到直线的距离公式等等来进行求解;第二点根据面积
的表达式,使用基本不等式、二次函数等知识求得面积的最值或取值范围.
22.已知函数 的最小值为0,其中 .
(1)求 的值;
(2)若对任意的 ,有 成立,求实数 的最小值;
(3)证明: .
【答案】(1) ;
(2) ;
(3)证明见解析.【分析】(1)对 进行求导,已知 最小值为0,可得极小值也为0,得 ,从而求出 的
值;
(2)由题意任意的 ,有 成立,可以令 先通过 , 大
致确定 取值范围,再利用分类讨论法求出 的最值;
(3)由(2)知:令 得: 令 得:
,累加即可的证.
【详解】(1)由函数 ,则其定义域为 ,且 .
由 ,得: ,又由 ,得: ,
在 单调递减,在 单调递增,
;
(2)设 ,
则 在 恒成立等价于 ,
注意到 ,又 ,
①当 时,由 得 .
在 单减, 单增,这与 式矛盾;
②当 时, 在 恒成立, 符合 ,
的最小值为 ;(3)由(2)知:令 得: ,
令 得:
当 时, (1);
当 时, ,
,
,
将(1)(2)(3),......,(n)式相加得:
不等式左边:
;
不等式右边:
;
所以 .
【点睛】方法点睛:对于含参函数的恒成立问题的处理,常采用两种方法:①参变分离求最值;②将左右
两边移到一边重新构造一个含参函数,讨论含参函数的单调性,确定哪一个点处取得最值.