2024届高三第二次模拟数学(理科)试卷_2024年4月_01按日期_21号_2024届宁夏银川一中高三下学期第二次模拟考试_宁夏回族自治区银川一中2024届高三下学期第二次模拟考试数学（理）试卷

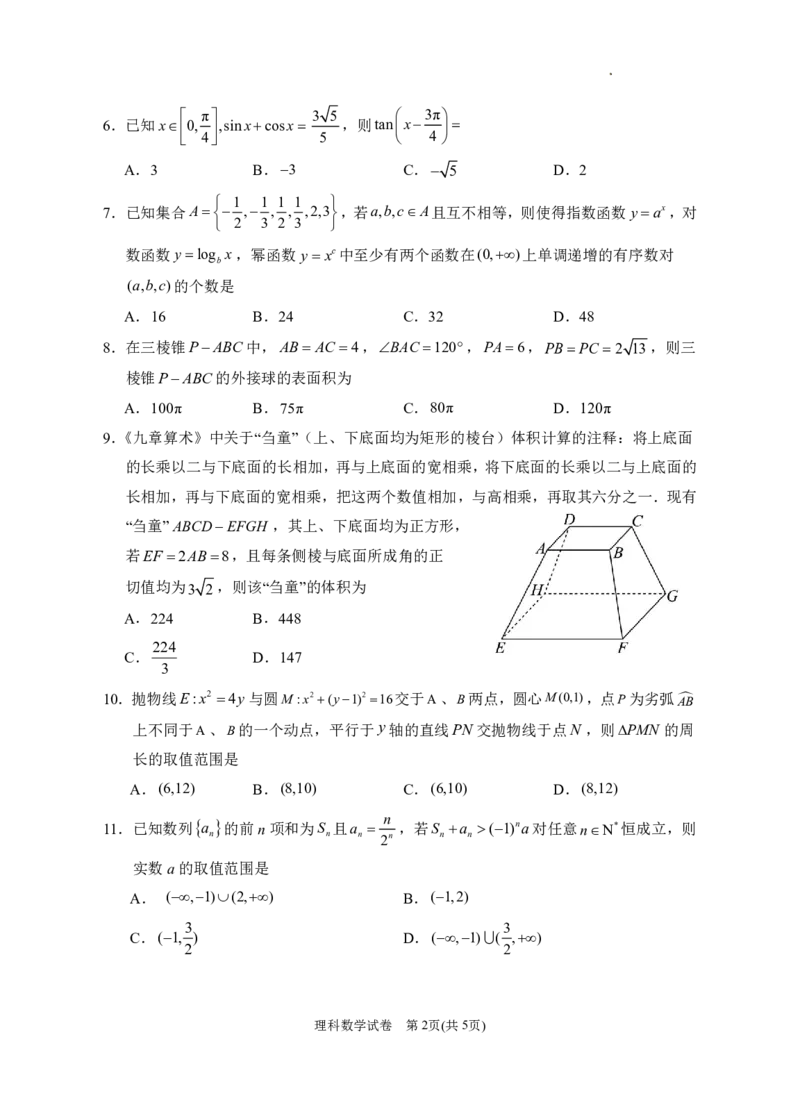
绝密★启用前 2024 年普通高等学校招生全国统一考试 理科数学试题卷 ( 银川一中第二次模拟考试 ) 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．作答时，务必将答案写在答题卡上。写在本试卷及草稿纸上无效。 3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中， 只有一项是符合题目要求的． 1．已知集合A  x∣x26x70  ,B{x∣2x6}，则AB A．,14, B．,1  4, C．,4 1, D． 7, ai 2．已知aR，若z 为纯虚数，则a 2i1 1 A． 2 B．2 C．1 D． 2 3．某几何体的三视图如图所示， 则该几何体的体积为 π π A． B． 6 2 π C． D．π 3 m 4．已知函数 f x1 mR为奇函数，则m的值是 3x 1 A．1 B．2 C．1 D．2 5．设O为平面直角坐标系的坐标原点，在区域 x,y x2 y2 4  内随机取一点，记该点 为A，则点A落在区域 x,y1x2y2 4  内的概率为 1 1 1 3 A． B． C． D． 8 4 2 4 理科数学试卷 第1页(共5页) 学科网（北京）股份有限公司 π 3 5  3π 6．已知x  0,  ,sinxcosx ，则tanx   4 5  4  A．3 B．3 C． 5 D．2  1 1 1 1  7．已知集合A , , , ,2,3，若a,b,cA且互不相等，则使得指数函数yax，对  2 3 2 3  数函数ylog x，幂函数y xc中至少有两个函数在(0,)上单调递增的有序数对 b (a,b,c)的个数是 A．16 B．24 C．32 D．48 8．在三棱锥PABC中，AB AC4，BAC120，PA6，PBPC  2 13，则三 棱锥PABC的外接球的表面积为 A．100π B．75π C．80π D．120π 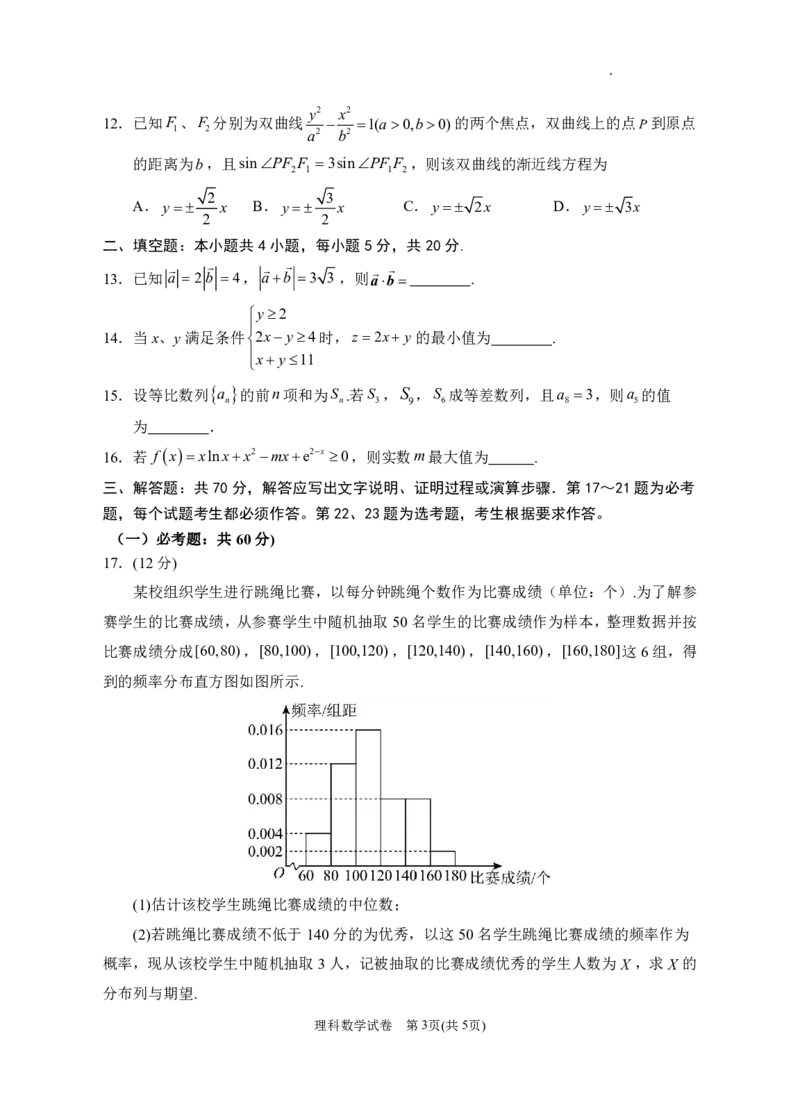9．《九章算术》中关于“刍童”（上、下底面均为矩形的棱台）体积计算的注释：将上底面 的长乘以二与下底面的长相加，再与上底面的宽相乘，将下底面的长乘以二与上底面的 长相加，再与下底面的宽相乘，把这两个数值相加，与高相乘，再取其六分之一．现有 “刍童”ABCDEFGH ，其上、下底面均为正方形， 若EF 2AB8，且每条侧棱与底面所成角的正 切值均为 3 2 ，则该“刍童”的体积为 A．224 B．448 224 C． D．147 3 10．抛物线E:x2 4y与圆M:x2(y1)2 16交于A、B两点，圆心M(0,1)，点P为劣弧AB 上不同于A、B的一个动点，平行于y轴的直线PN交抛物线于点N，则PMN 的周 长的取值范围是 A．(6,12) B．(8,10) C．(6,10) D．(8,12) n 11．已知数列a 的前n项和为S 且a  ，若S a (1)na对任意nN*恒成立，则 n n n 2n n n 实数a的取值范围是 A． (,1)(2,) B．(1,2) 3 3 C．(1, ) D．(,1)( ,) 2 2 理科数学试卷 第2页(共5页) 学科网（北京）股份有限公司y2 x2 12．已知F、F 分别为双曲线  1(a0,b0)的两个焦点，双曲线上的点P到原点 1 2 a2 b2 的距离为b，且sinPF F 3sinPFF ，则该双曲线的渐近线方程为 2 1 1 2 2 3 A．y x B．y x C．y 2x D．y 3x 2 2 二、填空题：本小题共4小题，每小题5分，共20分. 13．已知 a  2b  4， a  b  3 3，则a  b   . y2  14．当x、y满足条件2xy4时，z2xy 的最小值为 .  xy11 15．设等比数列a 的前n项和为S .若S ，S ，S 成等差数列，且a 3，则a 的值 n n 3 9 6 8 5 为 ． 16．若 f xxlnxx2mxe2x 0，则实数m最大值为 . 三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17～21题为必考 题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。 （一）必考题：共60分) 17．(12分) 某校组织学生进行跳绳比赛，以每分钟跳绳个数作为比赛成绩（单位：个）.为了解参 赛学生的比赛成绩，从参赛学生中随机抽取50名学生的比赛成绩作为样本，整理数据并按 比赛成绩分成[60,80)，[80,100)，[100,120)，[120,140)，[140,160)，[160,180]这6组，得 到的频率分布直方图如图所示. (1)估计该校学生跳绳比赛成绩的中位数； (2)若跳绳比赛成绩不低于140分的为优秀，以这50名学生跳绳比赛成绩的频率作为 概率，现从该校学生中随机抽取3人，记被抽取的比赛成绩优秀的学生人数为X ，求X 的 分布列与期望. 理科数学试卷 第3页(共5页) 学科网（北京）股份有限公司18.（12分） 已知平面四边形ABCD中，∠A+∠C=180°，BC=3. (1)若AB=6，AD=3，CD=4，求BD； 9 3 (2)若∠ABC=120°，△ABC的面积为 ，求四边形ABCD周长的最大值. 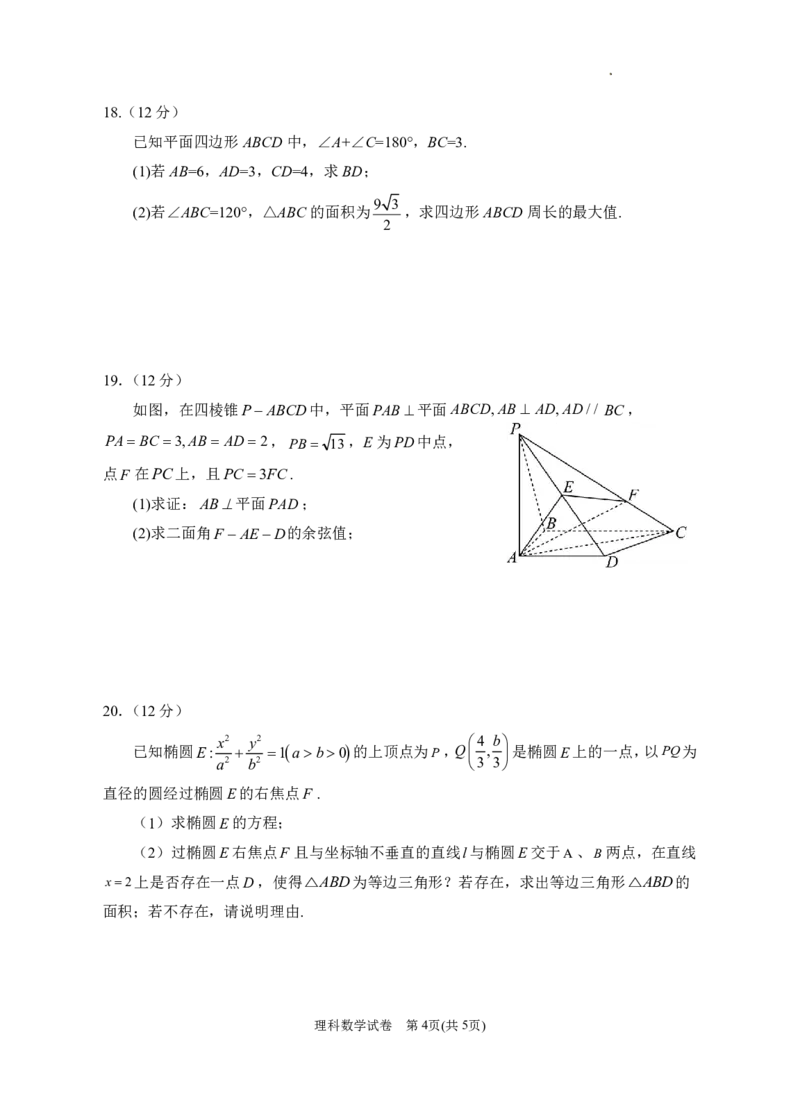2 19．（12分） 如图，在四棱锥PABCD中，平面PAB平面ABCD,AB AD,AD// BC， PABC 3,AB AD2， PB 13 ，E为PD中点， 点F 在PC上，且PC3FC. (1)求证：AB平面PAD； (2)求二面角FAED的余弦值； 20．（12分） x2 y2 4 b 已知椭圆E:  1ab0的上顶点为P，Q , 是椭圆E上的一点，以PQ为 a2 b2 3 3 直径的圆经过椭圆E的右焦点F . （1）求椭圆E的方程； （2）过椭圆E右焦点F 且与坐标轴不垂直的直线l与椭圆E交于A、B两点，在直线 x2上是否存在一点D，使得△ABD为等边三角形？若存在，求出等边三角形△ABD的 面积；若不存在，请说明理由. 理科数学试卷 第4页(共5页) 学科网（北京）股份有限公司21．（12分） 已知函数 f x xlnxax2 3xaR  . (1)若x1是函数 f x的一个极值点，求实数a的值； (2)若函数 f x有两个极值点x,x ，其中x x ， 1 2 1 2 ①求实数a的取值范围； ②若不等式2ax klnx 3k1恒成立，求实数k的取值范围. 1 2 （二）选考题：共10分.请考生在第22、23两题中任选一题做答，如果多做，则按所做的 第一题记分. 22．[选修4－4：坐标系与参数方程] xtcos, 在平面直角坐标系xOy中，直线l的参数方程为 （t为参数），以坐标原 y1tsin 点O为极点，x轴正半轴为极轴，建立极坐标系．曲线C的极坐标方程为22cos3． (1)求曲线C的直角坐标方程和直线l的一般方程； (2)设直线l与曲线C交于A、B两点，求△ABC面积的最大值． 23．[选修4-5：不等式选讲] 已知函数 f x x4 2 xa ，aR． (1)当a1时，解不等式 f x8； (2)若 f x3x2对任意x 1,2 恒成立，求a的取值范围． 理科数学试卷 第5页(共5页) 学科网（北京）股份有限公司