文档内容
2024 年 1 月“九省联考”考后提升卷
高三数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上
无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.现有一组数据: ,则这组数据的第85百分位
数是( )
A.652 B.668 C.671 D.674
2.已知椭圆 的上顶点、右顶点、左焦点恰好是等腰三角形的三个顶点,则
椭圆C的离心率为( )
A. B. C. D.
3.已知 为数列 的前 项和,且满足 ,则 ( )
A. B. C. D.
4..已知 , 为异面直线,直线 与 , 都垂直,则下列说法不正确的是( )
A.若 平面 ,则 ,B.存在平面 ,使得 , ,
C.有且只有一对互相平行的平面 和 ,其中 ,
D.至少存在两对互相垂直的平面 和 ,其中 ,
5.某学校举办运动会,径赛类共设100米、200米、400米、800米、1500米5个项目,田赛类共设铅
球、跳高、跳远、三级跳远4个项目.现甲、乙两名同学均选择一个径赛类项目和一个田赛类项目参
赛,则甲、乙的参赛项目有且只有一个相同的方法种数等于( )
A.70 B.140 C.252 D.504
6.在棱长为1的正方体 中, 在侧面 (含边界)内运动, 在底面
(含边界)内运动,则下列说法不正确的是( )
A. 若直线 与直线 所成角为30°,则 点的轨迹为圆弧
B. 若直线 与平面 所成角为30°,则 点的轨迹为双曲线的一部分
C. 若 ,则 点的轨迹为线段
D. 若 到直线 的距离等于 到平面 的距离,则点 的轨迹为抛物线的一部分
7.已知角 的终边上一点 的坐标为 ,则 的值为( )
A.0 B. C. D.
8.已知 , 分别为双曲线 : 的左,右焦点,点P为双曲线渐近线上一
点,若 , ,则双曲线 的离心率为( )A. B. C. D. 2
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.将函数 的图象向左平移 个单位长度,再将图象上所有点的横坐标变为原来的 倍
(纵坐标不变),得到 的图象,则( )
A. 函数 是偶函数
B. x=- 是函数 的一个零点
C. 函数 在区间 上单调递增
D. 函数 的图象关于直线 对称
10.已知z 与z 是共扼复数,以下四个命题一定是正确的是( )
1 2
A. B. C. D.
11.已知定义在 上的函数 满足 ,且 为奇函数,则下列说法一定
正确的是( )
A. 函数 的周期为
B. 函数 的图象关于 对称
C. 函数 为偶函数D. 函数 的图象关于 对称
三、填空题:本题共3小题,每小题5分,共15分.
12.已知集合 ,若 ,且 ,则实数 的取值范围是
__________.
13.甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分别为 和 ,体积
分别为 和 .若 ,则
14.已知数列 满足 , ,则 的前 项积的最大值为
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)设函数 , , ,已知曲线 在点
处的切线与直线 垂直.
(1)求a的值;
(2)求 的单调区间;
16.(15分)为倡导公益环保理念,培养学生社会实践能力,某中学开展了旧物义卖活动,所得
善款将用于捐赠“圆梦困境学生”计划.活动共计50多个班级参与,1000余件物品待出售.摄影社
从中选取了20件物品,用于拍照宣传,这些物品中,最引人注目的当属优秀毕业生们的笔记本,
已知高三1,2,3班分别有 的同学有购买意向.假设三个班的人数比例为6:7:8
(1)现从三个班中随机抽取一位同学:
(i)求该同学有购买意向的概率;
(ii)如果该同学有购买意向,求此人来自2班的概率;(2)对于优秀毕业生的笔记本,设计了一种有趣的“掷骰子叫价确定购买资格”的竞买方式:统一
以0元为初始叫价,通过掷骰子确定新叫价,若点数大于2,则在已叫价格基础上增加1元更新叫
价,若点数小于3,则在已叫价格基础上增加2元更新叫价;重复上述过程,能叫到10元,即获
得以10元为价格的购买资格,未出现叫价为10元的情况则失去购买资格,并结束叫价.若甲同学
已抢先选中了其中一本笔记本,试估计其获得该笔记本购买资格的概率(精确到0.01).
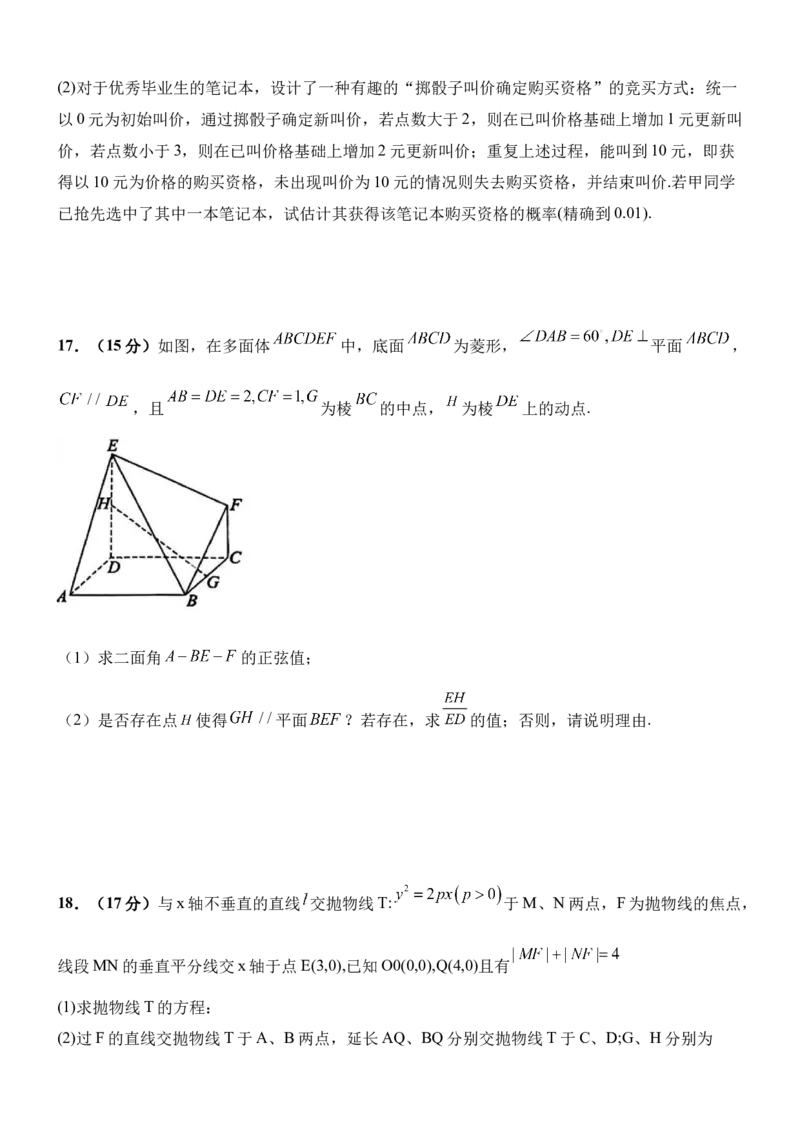
17.(15分)如图,在多面体 中,底面 为菱形, 平面 ,
,且 为棱 的中点, 为棱 上的动点.
(1)求二面角 的正弦值;
(2)是否存在点 使得 平面 ?若存在,求 的值;否则,请说明理由.
18.(17分)与x轴不垂直的直线 交抛物线T: 于M、N两点,F为抛物线的焦点,
线段MN的垂直平分线交x轴于点E(3,0),已知O0(0,0),Q(4,0)且有
(1)求抛物线T的方程:
(2)过F的直线交抛物线T于A、B两点,延长AQ、BQ分别交抛物线T于C、D;G、H分别为AB、CD的中点,求 的最小值.
19.(17分)对于无穷数列{a },设集合A={x|x=a ,n≥1}.若A为有限集,则称数列{a }为“T
n n n
数列”.
1
(1)已知数列{a }满足a =2,a = ,判断{a }是否为“T数列”,并说明理由;
n 1 n+1 1−a n
n
(2)设函数y=f(x)的表达式为f(x)=3|x+1|−|x+2|,数列{a }满足a =f (a ).若{a }为“T数
n n+1 n n
列”,求首项a 的值;
1
(3)设a =cos(tπn).若数列{a }为“T数列”,求实数t的取值集合.
n n