2024年三省三校联考一模数学答案(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024届东北三省三校第一次联考数学试题+答案

2024 年高三第一次联合模拟考试数学
参考答案
一.单项选择题
1-4 CABD 5-8 CBBB
二.多项选择题
9.ACD 10.ABD 11.ABD
三.填空题
12. 3 13. 5 14.
2 7
4
四.解答题
15.解：（1） f(x)=2cos2x−2sinx 2 
f ( 0 ) = 2 , f ( 0 ) = 2 4 
 f ( x ) 在 x = 0 处的切线方程为 y − 2 = 2 ( x − 0 ) ，即 y = 2 x + 2 6 
（2） f ( x ) = 2 c o s 2 x − 2 s i n x = 2 ( 1 − s i n 2 x ) − 2 s i n x = − 2 ( 2 s i n 2 x + s i n x − 1 ) 8 
f ( x )  0 则 − 2 ( 2 s i n 2 x + s i n x − 1 )  0 10
即 − 2 ( 2 s i n x − 1 ) ( s i n x + 1 )  0
即 s i n x 
1
2
解得 x ( 2 k
6
, 2 k
5
6
) , k Z
 
   + +  1 2 
故 f ( x ) 的单调递减区间为 ( 2 k
6
, 2 k
5
6
) , k Z
 
  + +  1 3 
16.解：（1）底面 A B C D 为平行四边形，
 A D C = 1 2 0 ,DAB=60 .
D A = 4 , A B = 8
由余弦定理可得：DB2 = AB2 + AD2 −2ABADcos60 =48DB=4 3
则 D A 2 + D B 2 = A B 2 ，  D A ⊥ D B 2
侧棱DD ⊥平面ABCD，DB平面ABCDDD ⊥DB 4
1 1
又 DA平面ADD A,DD 平面ADD A,且DA DD =D
1 1 1 1 1 1
DB⊥平面ADD A 6
1 1
又 AA 平面ADD A DB⊥ AA 7
1 1 1 1（2）四棱台中 A B C D − A
1
B
1
C
1
D
1
的体积为
2 8
3
3
 V =
1
3
( S
A B C D
+ S
A B1 C1 D1 1
+ S
A B C D
S
A B1 C1 D1 1
)

2 8
3
3
=
1
3
D D
1
( A D D B + A
1
D
1
D
1
B
1
+ A D D B A
1
D
1
D
1
B
1
)

2 8
3
3
=
1
3
D D
1
2 8 3 ,解得： D D
1
= 1 9 
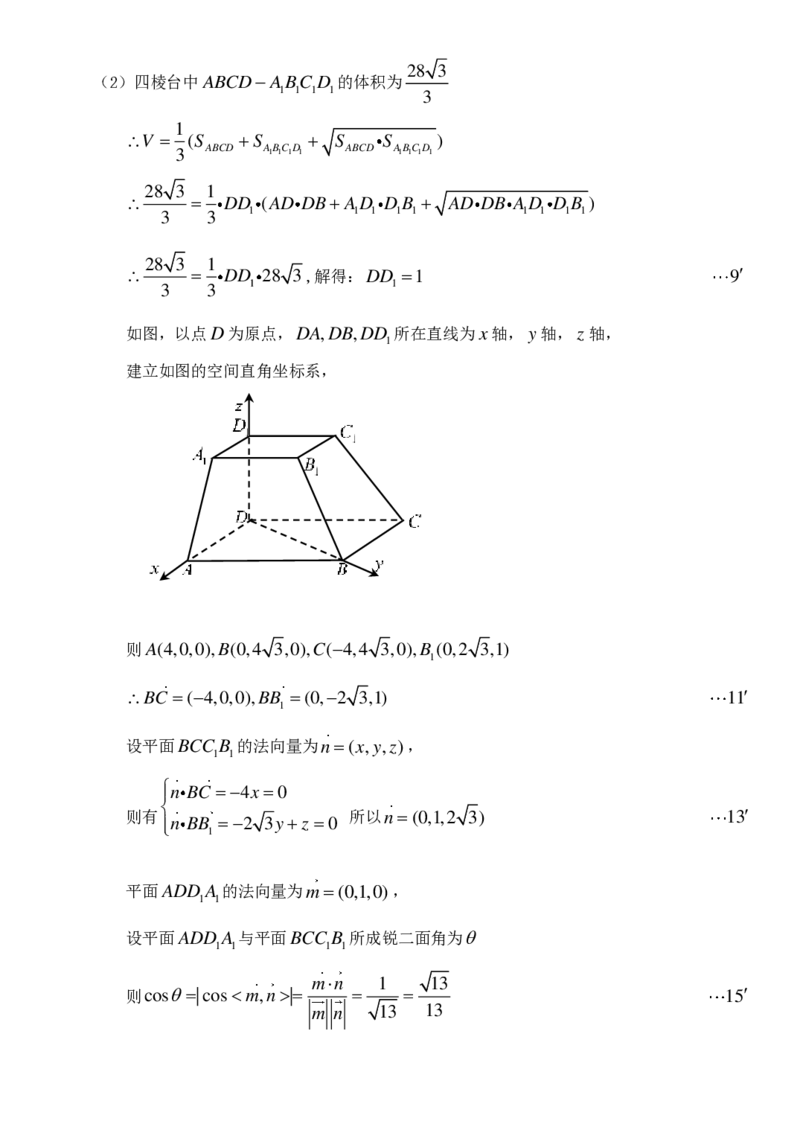
如图，以点 D 为原点， D A , D B , D D
1
所在直线为 x 轴， y 轴， z 轴，
建立如图的空间直角坐标系，
则 A ( 4 , 0 , 0 ) , B ( 0 , 4 3 , 0 ) , C ( − 4 , 4 3 , 0 ) , B
1
( 0 , 2 3 , 1 )
 B C = ( − 4 , 0 , 0 ) , B B
1
= ( 0 , − 2 3 , 1 ) 1 1 
设平面BCC B 的法向量为
1 1
n = ( x , y , z ) ，
 n BC =−4x=0

则有 所以n=(0,1,2 3)
 n BB =−2 3y+z =0
1
1 3 
平面 A D D
1
A
1
的法向量为m=(0,1,0)，
设平面 A D D
1
A
1
与平面 B C C
1
B
1
所成锐二面角为
mn 1 13
则cos=|cosm,n|= = = 15
m n 13 1317.解：（1）由图估计甲班平均分较高 3 
（2）由图可知，甲班中有
1
2
的学生分数低于128分；
乙班中有
3
4
的学生分数低于128分
设从两班中随机抽取一人，
“该同学来自甲班为事件A”，“该同学分数低于128分为事件B”，
则 P ( A ) =
1
2
, P ( A ) =
1
2
, P ( B A ) =
1
2
, P ( B A ) =
3
4
, 5 
 P ( B ) = P ( A B ) + P ( A B ) = P ( B A )  P ( A ) + P ( B A )  P ( A )
1 1 3 1 5
=  +  = 7
2 2 4 2 8
P ( A B ) =
P
P
( A
( B
B
)
)
=
P ( A )
P
P
(
(
B
B
)
A )
=
1
2

5
8
1
2
=
2
5
8
P ( A B ) =
P
P
( A
( B
B
)
)
=
P ( A )
P
P
(
(
B
B
)
A )
=
1
2

5
8
3
4
=
3
5
9 
所以，该同学来自甲乙两班的概率分别为
2
5
,
3
5
(3)依题 X 的所有可能取值为0,1,2,3 10
C3C0 1
P(X =0)= 6 4 =
C3 6
10
1 1 
P ( X = 1 ) =
C 26
C
C
31
0
14
=
1
2
12
P ( X = 2 ) =
C 16
C
C
31
0
24
=
1
3
0
1 3 
P ( X = 4 ) =
C 06
C
C
31
0
34
=
1
3 0
14
所以X 的分布列为:
15
18.解：（1）设M(x ,y ),N(x ,y )，则x +x =2,y + y =6
1 1 2 2 1 2 1 2
M,N 两点在双曲线C上
 x
a
x
a
2
12
2
22
−
−
y
b
y
b
2
12
2
22
=
=
1
1
①
②
，由①−②得
x
1
2 −
a 2
x
2
2
−
y
1
2 −
b 2
y
2
2
= 0
即
y
x
1
1
2
2
−
−
y
x
2
2
2
2
=
b
a
2
2
， 
(( y
x
1
1
+
+
y
x
2
2
)) (( y
x
1
1
−
−
y
x
2
2
))
=
b
a
2
2
2
 k
O Q
 k
M N
=
b
a
2
2
，即  1  3 =
b
a
2
2
, b 2 = 3 a 2
又 a=1,b2 =3，双曲线 C 的方程为： x 2 −
y
3
2
= 1 4 
（2）由已知可得，直线 M N 的方程为：y−3=1(x−1)，即 y = x + 2
联立

3 x 2
y
−
=
y
x
2
+
−
2
3 = 0
 2 x 2 − 4 x − 7 = 0 ,  = 1 6 + 5 6 = 7 2  0 6 
则 x
1
+ x
2
= 2 , x
1
x
2
= −
7
2
8 
E M  E N = ( x
1
− 1 , y
1
)  ( x
2
− 1 , y
2
) = ( x
1
− 1 ) ( x
2
− 1 ) + y
1
y
2
= ( x
1
− 1 ) ( x
2
− 1 ) + ( x
1
+ 2 ) ( x
2
+ 2 ) = 2 x
1
x
2
+ ( x
1
+ x
2
) + 5
= 2  ( −
7
2
) + 2 + 5 = 0
 E M ⊥ E N ，EMN为直角三角形 1 0 
（3）由题意可知，若直线AB有斜率则斜率不为0，
故设直线 A B 方程为： x = m y + n
设 P ( x
3
, y
3
) , A ( x
4
, y
4
) , B ( x
5
, y
5
)
A P P B , ( x
3
x
4
, y
3
y
4
) ( x
5
x
3
, y
5
y
3
)   =  − − = − −
 x +x
x = 4 5
x −x =(x −x )   3 1+
 3 4 5 3 
 y 3 − y 4 =(y 5 − y 3 )  y = y 4 +y 5
 3 1+点P在双曲线 C 上，
x
41
1
x
5
2
y
41
3
y
5
2
1
 
 

 +
+

−
 +
+

=
3(x +x )2 −(y +y )2 =3(1+)2
4 5 4 5
( 3 x 24 y 24 ) 2 ( 3 x 25 y 25 ) 2 ( 3 x
4
x
5
y
4
y
5
) 3 ( 1 ) 2     − + − + − = + ③
又 3 x 24 − y 24 = 0 , 3 x 25 − y 25 = 0 ，
2 ( 3 x
4
x
5
y
4
y
5
) 3 ( 1 ) 2    − = +
3(1+)2
，3x x − y y = ④
4 5 4 5 2
联立
 3 x
x
2
=
−
m
y
y
2
+
=
n
0
 ( 3 m 2 − 1 ) y 2 + 6 m n y + 3 n 2 = 0

 = 3 6 m 2 n
3 m
2 −
2
1
−
2
1
n

2 (
0
3 m 2 − 1 )  0
 m  
3
3
−6mn 3n2
y + y = ⑤,y y = ⑥ 14
4 5 3m2 −1 4 5 3m2 −1
A , B 分别在第一象限和第四象限，  y
4
y
5
 0 , 3 m 2 − 1  0
由④式得： 3 ( m y
4
n ) ( m y
5
n ) y
4
y
5
3 (1
2
) 2 

+ + − =
+
( 3 m 2 1 ) y
4
y
5
3 m n ( y
4
y
5
) 3 n 2
3 ( 1
2
) 2 

 − + + + =
+
⑦
3n2 −6mn 3(1+)2
将⑤⑥代入⑦得：(3m2 −1) +3mn +3n2 =
3m2 −1 3m2 −1 2
−6n2 3(1+)2
 =
3m2 −1 2
1 3 2 3 2 3
S = OA OB sinAOB=   y   y
AOB 2 4 3 1 3 2
3 3 3n2 n2 1 3(1+)2 3  1 
= y y = =− 3 =  =

+ +2

15
3 1 2 3 3m2−1 3m2−1 2 3 2 4 3  令 h ( )
1
, [
1
3
, 2 ]   

= + 
h ( ) 1
1
2
( 1 ) (
2
1 )
, [
1
3
, 2 ]
 
 
 
 = − =
+ −

1
3
, 1 , h ( ) 0    
 
  ， h ( )  单调递减
( 1 , 2  , h ( ) 0      ， h ( )  单调递增
10
h()[2, ]， 16
3
 S
 A O B


3 ,
4
3
3 
17
19.（1）证明： 8 n + 3 = a
0
 2 k + 3 + a
1
 2 k + 2 + + a
k
 2 3 + 1  2 1 + 1
S(8n+3)=a +a + +a +1+1=S(n)+2
0 1 k
3 
4n+3=a 2k+2 +a 2k+1+ +a 22 +121+1
0 1 k
 S ( 4 n + 3 ) = a
0
+ a
1
+ + a
k
+ 1 + 1 = S ( n ) + 2 6 
S(8n+3)=S(4n+3) 7 
（2）（Ⅰ）解： 6 0 = 3 2 + 1 6 + 8 + 4 = (1 1 1 1 0 0 )
2
 I ( 6 0 ) = 2 1 0 
（Ⅱ）解： 1 = ( 1 )
2
， 5 1 1 = (1 1 1 1 1 1 1 1 1 )
2
，故从n=1到 n = 5 1 1 中
𝐼(𝑛)=0有9个，
𝐼(𝑛)=1有𝐶1+𝐶1+⋯𝐶1 =𝐶2个，
1 2 8 9
𝐼(𝑛)=2有𝐶2+𝐶2+⋯𝐶2 =𝐶3个，
2 3 8 9
……，
𝐼(𝑛)=9有𝐶8 =𝐶9 =1个，
8 9
511
∑2𝐼(𝑛) =9×20+𝐶2×21+𝐶3×22+⋯𝐶9×28
9 9 9
𝑛=1
13𝐶1×21+𝐶2×22+𝐶3×23+⋯𝐶9×29
9 9 9 9
=
2
𝐶0×20+𝐶1×21+𝐶2×22+𝐶3×23+⋯𝐶9×29−1
9 9 9 9 9
=
2
1 6 
(1+2)9−1
= =9841
2
1 7 