2024年二诊数学诊断答案_2024年4月_01按日期_21号_2024届甘肃省高三下学期4月月考试卷（二模）_2024届甘肃省高三下学期4月月考试卷（二模）数学

2024 年甘肃省高三月考（4 月） 数学试题答案及评分参考 一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 题号 1 2 3 4 5 6 7 8 答案 C A B C B D D A 8. 解析：因为 f(x) f(2x)，所以函数 f(x)关于x1成轴对称， 又因为x[1,)时， f(x)=ex ex，所以 f(x)在x[1,)上为增函数，故 f(x)在 7 2 (,1]为减函数.所以距离x1越远值越大，因为1sin 0，而123 2， 5 7 0log 31，距离x1最远的为sin ，所以c最大. 4 5 16 log 3（0,1）且 f(log 3) f(2log 3) f(log )， 4 4 4 4 3 2 16 2 16 因为123 2且1log 2，均在函数的增区间(1,)上，故分别比较23和log 4 3 4 3 3 2 3 27 32 2 2 3 与 的大小，而(23)3 4，( )3   (23)3，所以得23  ， 2 2 8 8 2 16 3 3 16 2 又因为log log 8log (4)2  ，所以 f(log ) f(23)，即ab. 4 3 4 4 2 4 3 综上有：cab，故选A. 二、选择题：本大题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符 合题目要求。全部选对的得6分，部分选对的得部分分（9,10题答对一个选项得3分， 11题答对一个选项得2分），有选错的得0分。 题号 9 10 11 答案 AD BD ABD 11.解析：因为直线l ，l 平行于x轴，所以设点P(x,y )，Q(x ,y )，且由抛物线的光学 1 2 1 1 2 2 性质知直线PQ经过抛物线y2 2pxp0的焦点F，设直线PQ的方程为： p xny ， 2 高三月考 数学答案 第1页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}与y2 2px联立，消去x得y2 2pny p2 0，所以有y y p2， 1 2 y2 y2 p2 xx  1  2  1 即 p2，抛物线的标准方程为y2 4x，故选项A正确； 1 2 2p 2p 4 对于选项B，当y 2p，则有点P(2p,2p)，又因为直线PQ经过抛物线 1 p p y2 2pxp0的焦点F，则有y y p2，所以有Q( , )，又根据抛物线的定义 1 2 8 2 可得： p p p 25 25 1 |PQ|2p    p ，所以 p2.于是有P(4,4)，Q( ,1).所以得直线 2 8 2 8 4 4 PQ的方程为4x3y40，故选项B正确； 对于选项C，因为直线l ，l 间的最小距离为8，即2p8，所以 p4. 1 2 又因为光线的路程为APPQQB5x x x  p5x 14，故选项C不正确； 1 1 2 2 对于选项D，因为直线PQ经过抛物线y2 2pxp0的焦点F，则有 y y p2，又因为y y 4，所以 p2，抛物线的标准方程为y2 4x.又因为抛物 1 2 1 2 线y2 4x的焦点F1,0,准线为x1,所以设直线PQ:xmy1,与y2 4x联 立,消去x,整理得: y2 4my40,设P(x,y ),Q(x ,y ),M(1,t)， 1 1 2 2 y  y 4m, 有 1 2 y y 4.  1 2 t y t y t x 1y tx 1y t 易知k 3  2 ,而 k 1 k 2  x 1 1  x 2 1  2 x 1 1x 1 1 2 1 2 1 2  y2   y2   4 2 1 y 1 t 4 1 1 y 2 t t  4m2 4        t 2k  y2  y2  4m2 4 3  1 1 2 1 4 4    故选项D正确. 三、填空题：本大题共3小题，每小题5分，共15分。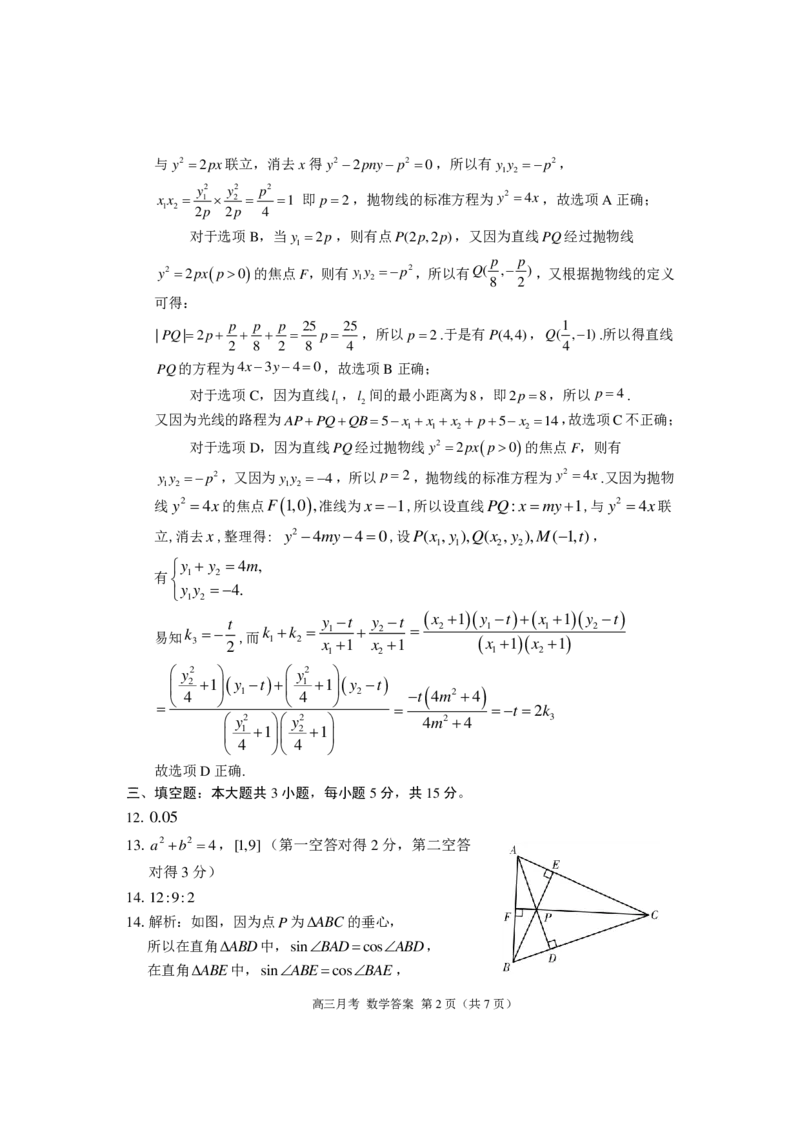 12.0.05 13.a2 b2 4，[1,9]（第一空答对得2分，第二空答 对得3分） 14.12:9:2 14.解析：如图，因为点P为ABC的垂心， 所以在直角ABD中，sinBADcosABD， 在直角ABE中，sinABEcosBAE， 高三月考 数学答案 第2页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}PA PB 又因为在PAB 中，  ， sinABP sinBAP PA sinABP cosBAC 所以  = ， PB sinBAP cosABC PA sinACP cosBAC 同理  = ， PC sinCAP cosACB 所以PA:PB:PCcosBAC:cosABC:cosACB, 3 9 1 又因为a:b:c=4:5:6，所以cosBAC , cosABC , cosACB , 4 16 8 所以x:y:z12:9:2. 四、解答题：本大题共5小题，共77分。解答应写出必要的文字说明、证明过程或演算 步骤。 15．（13分）   解：（1）因为2，所以 f(x)sin(2x )，故 f '(x)2cos(2x )， 6 6 1 f(x)在点(0, )处的切线斜率k  f'(0) 3， 2 1 1 所以在点(0, )处的切线方程为y 3x ，即2 3x2y10. ……………6分 2 2  （2）g(x) f '(x)cos(x ) ， 6   因为g(x)在[0, ]上为减函数，所以g'(x)0在[0, ]上恒成立， 2 2     即2sin(x )0在[0, ]上恒成立，化简为sin(x )0在[0, ]上恒成立， 6 2 6 2      因为x[0, ]，故x [ ,  ]， 2 6 6 2 6   5 根据正弦函数的图象与性质可得，只需  ，解得 ， 2 6 3 5 故的取值范围为(0, ]. 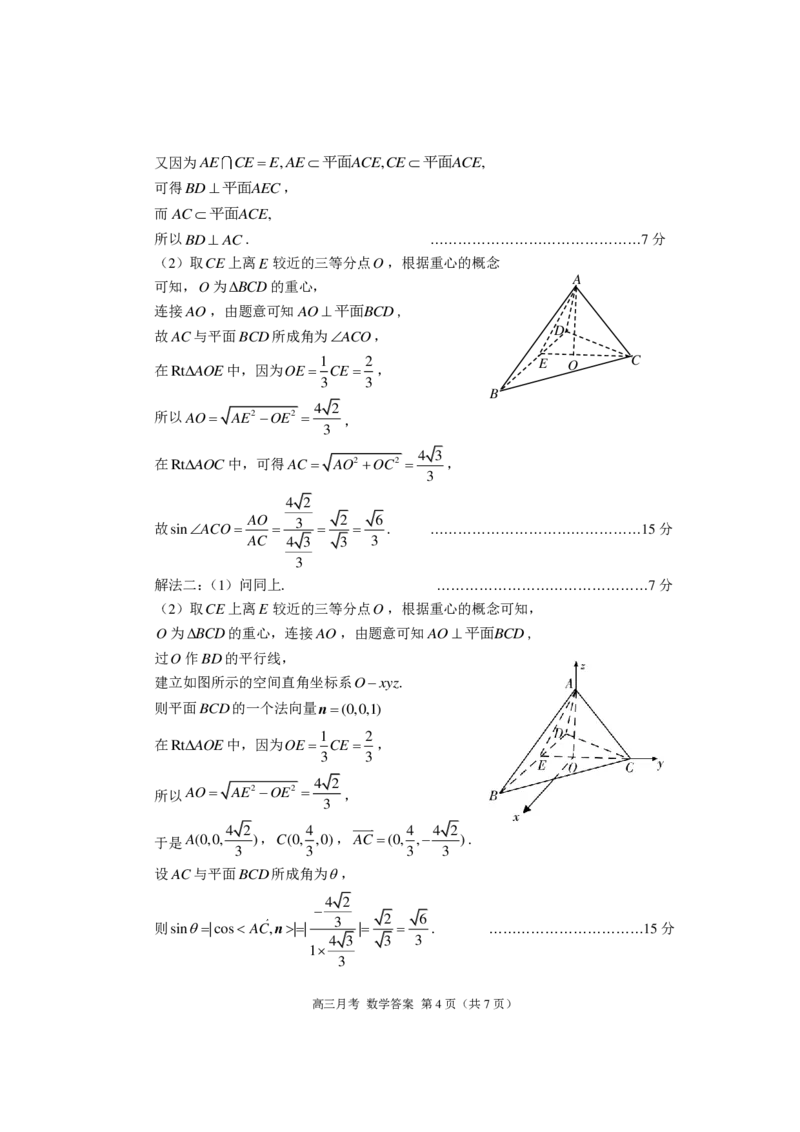……………13分 3 16．（15分） 解法一：（1）证明：如图，取BD的中点E ， 连接AE和CE. 因为ABD和BCD是底边为BD的等腰三角形， 所以BDAE且BDCE， 高三月考 数学答案 第3页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}又因为AE CEE,AE平面ACE,CE平面ACE, 可得BD平面AEC， 而AC平面ACE, 所以BDAC. ………………………………………7分 （2）取CE上离E 较近的三等分点O，根据重心的概念 A 可知，O为BCD的重心， 连接AO，由题意可知AO平面BCD, D 故AC与平面BCD所成角为ACO， 1 2 E EO C 在RtAOE中，因为OE CE ， 3 3 B 4 2 所以AO AE2 OE2  ， 3 4 3 在RtAOC中，可得AC AO2 OC2  ， 3 4 2 AO 3 2 6 故sinACO    . ………………………………………15分 AC 4 3 3 3 3 解法二：（1）问同上. ………………………………………7分 （2）取CE上离E 较近的三等分点O，根据重心的概念可知， O为BCD的重心，连接AO，由题意可知AO平面BCD, 过O作BD的平行线， 建立如图所示的空间直角坐标系Oxyz. 则平面BCD的一个法向量n(0,0,1) 1 2 在RtAOE中，因为OE CE ， 3 3 4 2 所以AO AE2 OE2  ， 3 4 2 4 4 4 2 于是A(0,0, )，C(0, ,0)，AC(0, , ). 3 3 3 3 设AC与平面BCD所成角为， 4 2  3 2 6 则sin|cos AC,n|| |  . ……………………………15分 4 3 3 3 1 3 高三月考 数学答案 第4页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}17．（15分） n2 n 解：（1）因为2S n2 n，所以S  ， n n 2 n2 n (n1)2 (n1) 当n2时，a S S   n, n n n1 2 2 因为a 1也满足上式，故a n(nN*). ……………5分 1 n 1 （2）因为b  ，且a n(nN*)， n a  a n n n1 1 n1 n 所以b    n1 n , n n n1 ( n n1)( n1 n) 所以 T =( 2 1)( 3 2)+( 4 3)+ +( 100 99)= 10019， 99 即T =9. ……………………………10分 99 （3）由于 1  1  1  1  n1 n ， 2 a 2 n n n n n1 n 1 1 1 1 故      21 3 2  100 99 2 a 2 a 2 a 2 a 1 2 3 99  10019. 所以原不等式成立. …………………………15分 18．（17分） 解：（1）设高一年级学生踢毽子“达标”的指标界值为x，分析得x(45,50), 依题意有：(x45)0.060.6(0.010.0240.0360.040)5 0.05 即x45 46. ………………………………………5分 0.06 （2）设第i次传踢之前毽子在乙、丙的概率为b i ，c i 则有bici 1 2 ai ，a i1  1 2  1 2 ai  1 2  1 2 ai  1 2 ai ， 所以a  ai  1 ，即有：a  1  1 （a  1 ） (iN *), i1 2 2 i1 3 2 i 3 所以  a  1 为等比数列，其中首项为a  1  2 ，公比为  1 ，即a  1  2 （ 1 ）i1 ,  i 3 1 3 3 2 i 3 3 2 1 2 1 5 所以a   （ ）i1(iN*) ，a  . …………………………………13分 i 3 3 2 6 16 1 1 i为偶数时，a  ，b c  ，毽子在乙、丙的概率较大， i 3 i i 3 1 1 i为奇数时，a  ，b c  ，毽子在甲的概率较大. ……………………17分 i 3 i i 3 高三月考 数学答案 第5页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}19．（17分) 解：（1）因为点M(0, 2)，所以M所在的曲线方程为y 2x2 ， x 2 2 1 故y' ，y'' ，y'| 0，y''|   ， 2x2 3 x0 x0 3 2 (2x2)2 (202)2 故曲线C 在点M(0, 2)处的曲率为 1 |y''| 1 K   . …………………………………4分 3 2 (1 y'2)2 1 1 2 又因为曲线C :xy1的方程可写为y ，故y' ，y'' ， 2 x x2 x3 2 | | x3 1 故 E  ，解得x 1， 1 3 2 E (1 )2 x4 E 所以E(1,1)或E（1，1）（注：只需写出一个点即可得满分）. ……………………7分 （2）由题干可知，半径最大的圆为在该点处的密切圆即曲率圆， 1 所以半径  2 ，而圆心在点M(0, 2) y K y 处的法线上，故圆心D(0,2 2)， P P 所以半径最大的圆的方程为： A x2 (y2 2)2 2. ………………11分 （3）解法一：因为A，B为曲线C1上关于 O 原点对称的两点，故A，B的中点为O，所以 x 2 2 PAPB(POOA)(POOB)PO OA 2 2  PO  OA （*） B 所以当 PO 取最大且 OA 取最小时，（*）式 取最大， 因为|PO| 3 2，|OA|  2 ， max min 故(PAPB) 18216. ……………………………17分 max 解法二：设P(x ,y )，A(x ,y ),B(x ,y )， 0 0 1 1 1 1 高三月考 数学答案 第6页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}则PAPB(x x ,y y )(x x ,y  y ) 0 1 0 1 0 1 0 1 x 2 x2 y 2 y2 (x2 y2)(x2 y2) 0 1 0 1 0 0 1 1 其中x2  y2表示圆上点到原点的距离的平方，所以(x2  y2) (3 2)2 18， 0 0 0 0 max 而x2 y2 22y2，所以当y2取最小值2时，x2 y2取最大值，最大值为-2， 1 1 1 1 1 1 故(PAPB) 18216. ……………………………17分 max 高三月考 数学答案 第7页（共7页） {#{QQABAQSAogAoAIIAARhCUQVgCEIQkBACCKoGAFAIIAIBiQFABAA=}#}