文档内容
2024 年第四届章鱼杯联考(高中组)
数 学
注意事项:
1.本试卷分选择题和非选择题两部分,满分 150 分,考试时间 120 分钟。
2.答题前,考生务必用直径0.5 毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂
黑;非选择题用直径0.5 毫米黑色墨水签字笔在答题卡上各题的答题区内作答,超出答题区域书写的答案无效,在
试卷、草稿纸上作答无效。
一、选择题:本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 方程 logx(x+2024) = 2 的实数解的个数是
A.0 B.1 C.2 D.3
2.记i 为虚数单位,n为正整数,若(3+ 4i)ⁿ 位于复平面的第四象限,则 n的最小值为
A.4 B.5 C.6 D.7
3. 若三次函数 f(x) 满足 f(0) =0,f(1)= 1,f'(0)=3,f'(1) = 9, 则 f(3)=
A.38 B.171 C.460 D.965
4. 设p是q 的充分不必要条件,-p是 -rr的必要不充分条件,则
A. p是qVr的充分不必要条件; B. p是 q∧r的充分不必要条件;
C. p是q∧r的必要不充分条件; D. p是q∨r的必要不充分条件.
5. 设 A 在曲线 上, B在直线y=2x-3上,O为坐标原点,则 的最小
值是 𝑦𝑦=𝑙𝑙𝑙𝑙𝑙𝑙−𝑙𝑙²+3𝑙𝑙−1 |�𝑂𝑂���𝑂𝑂�⃗+𝑂𝑂����𝑂𝑂�⃗|
√5 2√5 3√5 4√5
6. 一𝑂𝑂次. 5铁人三项比赛中,每名𝑂𝑂参.赛5选手须在指定的游泳𝐶𝐶池.里5游 20 个来回,然后𝐷𝐷骑.车5 10 公里,最后跑 3 公里. 已知
共有 n名选手参赛,由于场地条件限制,游泳池内只能同时容纳一名选手(即上一名选手上岸时下一名选手方可下水),
骑车与跑步则无限制. 记序号为 i 的选手游泳、骑车、跑步所用时长的期望分别为 si,b,r.为了使得总完赛时间
(即从 1 号选手下水到n号选手跑完的总时长) 尽可能短,应采取的策略是 ᵢ ᵢ
A. 让 s 越大的选手越早出发 B. 让 s 越小的选手越早出发
C. 让 ᵢ 越大的选手越早出发 D.让 ᵢ 越小的选手越早出发
7.给定 k∈R𝑏𝑏,ᵢ +若𝑟𝑟;m>0, x,y∈R 满足 cosx+kcosy=1, 𝑏𝑏 ᵢ+ 𝑟𝑟 ᵢ 均有|y|≥m,则k的范围是
A.(-∞,0)∪(∃2,+∞)∀ B.(-∞,0]∪[2,+∞)
C. [0,2] D.(0,2)
8. Enigma机是二战时用来加密和解密的设备,其中插线板是整套密码系统的一环,原理如下:有 26 根接线柱对应26
个英文字母,另有k条导线,每条导线的两端接在某两根不同的接线
第四届章鱼杯高中组·数学 第1页( 共 5 页)
学科网(北京)股份有限公司柱上,每根接线柱上至多连一条导线,以此交换输入的文字中有导线相连的接线柱处的字母.例如, k=2时,
设O与P 相连, G 与S 相连, 输入文字 BIGOCTOPUS, 则交换 O 与P, 交换 G 与S, 故输出 BISPCTPOUG. 设不
同的接线方法数为 ak: 若 ak越大则这套密码系统越安全. 要使安全性最高,k应该取
A.7 B.9 C.11 D.13
二、选择题:本题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,有多项符合题目要求,全
部选对的得 6 分,部分选对的得部分分,有选错的得 0 分.
9. 记集合 A ={n∈ N₊|正n边形可用尺规作出}, 熟知3,4,5∈ A, 7,9,11 ∉ A, 则以下角中能被尺规作出的是
A.21° B.25° C.48° D.62°
10.下列关于异面直线的断言正确的是
A.给定异面直线 a,b, 定长线段 AB,CD分别在a,b上滑动, 则四面体 ABCD 的体积不变;
B.设 a,b为异面直线, 夹角为θ, 点A在a上, 点B在b上, |AB|=l, AB 与a,b的夹角分别是 90°和α,则a,
b之间的距离为
2
cos 𝛼𝛼
C. 设 a,b为异面直线𝑙𝑙�,1则−空si间n 2 𝜃𝜃内;存在某些点 P,使得过 P 的直线不可能与 a,b均相交;
D.存在两两异面的直线 a,b,c和相交直线 m,n, m与a,b,c均相交, n与a,b,c 均相交.
11.有n个进程(n≥3) q₁,q₂,···,qn要访问一个数据库,不同进程之间、 同一进程在不同时刻是否尝试访问
数据库是相互独立的,且每一秒每个进程尝试访问数据库的概率均为¹/n. 若某一秒恰有一个进程访问数据库,则
访问成功,否则访问失败. 以下是一个 n =4 的样例:
序号/时刻 第 1 秒 第2 秒 第 3 秒 第 4 秒 第 5 秒 第 6 秒 第7秒
q₁ ✔ ✔ ✔
q2 ✔ ✔ ✔
q₃ ✔ ✔
q₄ ✔
访问结果 q₁ qa 失败 q₂ 失败 失败 q₃
记 Xi(t) 为 qi 在前 t 秒成功访问数据库的次数,e 为自然对数的底,[x] 表示不小于实数 x 的最小整
数,下列说法正确的是
A.若n=4, 则 ;411
4 27 𝑡𝑡 𝑡𝑡
∑ 𝑖𝑖=1𝑃𝑃(𝑋𝑋𝑖𝑖(1)=0)=64; 𝑂𝑂.𝑒𝑒𝑒𝑒<𝑄𝑄�𝑋𝑋1(𝑡𝑡)�<2𝑒𝑒
1 𝑒𝑒 1
𝐶𝐶.𝑃𝑃(𝑋𝑋1([𝑒𝑒𝑙𝑙])=0)≤𝑒𝑒; 𝐷𝐷.𝑃𝑃��𝑖𝑖=1 {𝑋𝑋𝑖𝑖(2[𝑒𝑒𝑙𝑙][ln𝑙𝑙])≥1}�≥1−𝑒𝑒
三、填空题: 本题共 3 小题, 每小题 5 分, 共 15 分.
12. 已知正七边形 ABCDEFG 的外接圆为 且 A 为该圆上距离坐标原点最远
的点,则关于这七个点的回归直线方程为 ; 设 CG,AD 交于 Q,则
(𝑙𝑙−1)²+(𝑦𝑦−2)² =3,
𝑄𝑄𝑄𝑄
13. 设 {a₁,a₂,. ..,a₉} = {1,2,...,9}, 且 则满𝐷𝐷𝑄𝑄足=要求¯ .的数列 的个
数是 . 𝑎𝑎₂ᵢ₋₁>𝑎𝑎₂ᵢ<𝑎𝑎₂ᵢ₊₁,∀𝑖𝑖∈1,2,3,4, {𝑎𝑎𝑙𝑙 } 1≤𝑙𝑙≤9
第四届章鱼杯高中组·数学 第2 页( 共 5 页)
学科网(北京)股份有限公司14. 设双曲线 Γ: A(0,2), B,C 在 Γ 上且直线 BC 经过 A. 设 lB, lc 分别为Γ在 B,C 处的切线, 点
D 满足 𝑙𝑙²−3𝑦𝑦²=,− 3则, D 的轨迹方程是 ;若 D 的横纵坐标均为正整数,且二者之和大于 2024,
则 D 可以是 𝑂𝑂 𝐷𝐷 ⟂ 𝑙𝑙 𝐵𝐵 ,𝐶𝐶(写𝐷𝐷⊥出𝑙𝑙 𝐶𝐶个, 即可)
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. (13 分)
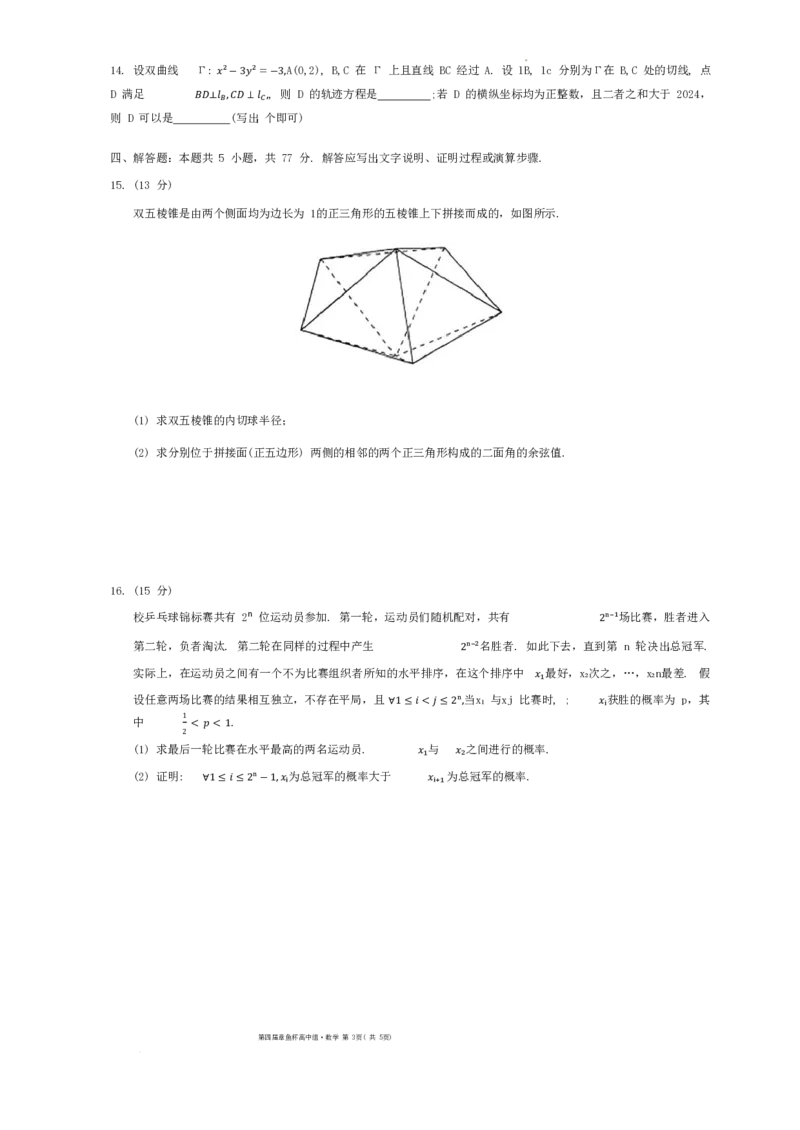
双五棱锥是由两个侧面均为边长为 1的正三角形的五棱锥上下拼接而成的,如图所示.
(1) 求双五棱锥的内切球半径;
(2) 求分别位于拼接面(正五边形) 两侧的相邻的两个正三角形构成的二面角的余弦值.
16. (15 分)
校乒乓球锦标赛共有 2ⁿ 位运动员参加. 第一轮,运动员们随机配对,共有 场比赛,胜者进入
第二轮,负者淘汰. 第二轮在同样的过程中产生 名胜者. 如此下去,直到2ⁿ第⁻¹ n 轮决出总冠军.
实际上,在运动员之间有一个不为比赛组织者所知的水平排序,在2ⁿ这⁻²个排序中 最好,x₂次之,…,x₂n最差. 假
设任意两场比赛的结果相互独立,不存在平局,且 当x₁ 与xj 比赛𝑙𝑙₁时, ; 获胜的概率为 p,其
中 ∀1≤𝑖𝑖<𝑗𝑗≤2ⁿ, 𝑙𝑙ᵢ
1
(1) 求最后2一<轮𝑝𝑝 <比赛1.在水平最高的两名运动员. 与 之间进行的概率.
(2) 证明: 为总冠军的概率大于 𝑙𝑙₁ 为𝑙𝑙总₂冠军的概率.
∀1≤𝑖𝑖≤2ⁿ−1,𝑙𝑙ᵢ 𝑙𝑙ᵢ₊₁
第四届章鱼杯高中组·数学 第 3页( 共 5页)
学科网(北京)股份有限公司17. (15 分)
17世纪德国天文学家约翰内斯·开普勒提出描述行星运动的三大基本定律:
(a) 行星绕太阳运动的轨道为椭圆(圆可视为特殊的椭圆),太阳位于椭圆的一个焦点上,所有行星的
轨道可近似看成在同一平面内;
(b) 行星在其椭圆轨道上的相等时间内,与太阳连线所扫过的面积相等.
(c) 行星的公转周期的平方与它们的椭圆轨道长轴的立方成正比.
开普勒三定律为我们理解行星运动提供了重要的基础,并且被广泛应用于天体力学和行星轨道计算中。
设 a,b, 地球、太阳、火星均可视为点,太阳位于 地球的公转轨道可近
似看成圆 𝑐𝑐 > 0, 𝑎𝑎²=𝑏𝑏²+𝑐𝑐², 火星的公转轨道可近似看成圆 (−𝑐𝑐,0), 且
火星的公转周期𝐶𝐶约₁:为(𝑙𝑙地+球𝑐𝑐)公²+转𝑦𝑦周²=期(的𝑎𝑎− 1𝑐𝑐.)8²8,2 倍. 霍曼转移轨道 E 是以太阳𝐶𝐶₂所:(𝑙𝑙在+位𝑐𝑐置)²为+𝑦𝑦其²中=一(𝑎𝑎个+焦𝑐𝑐)点², ,
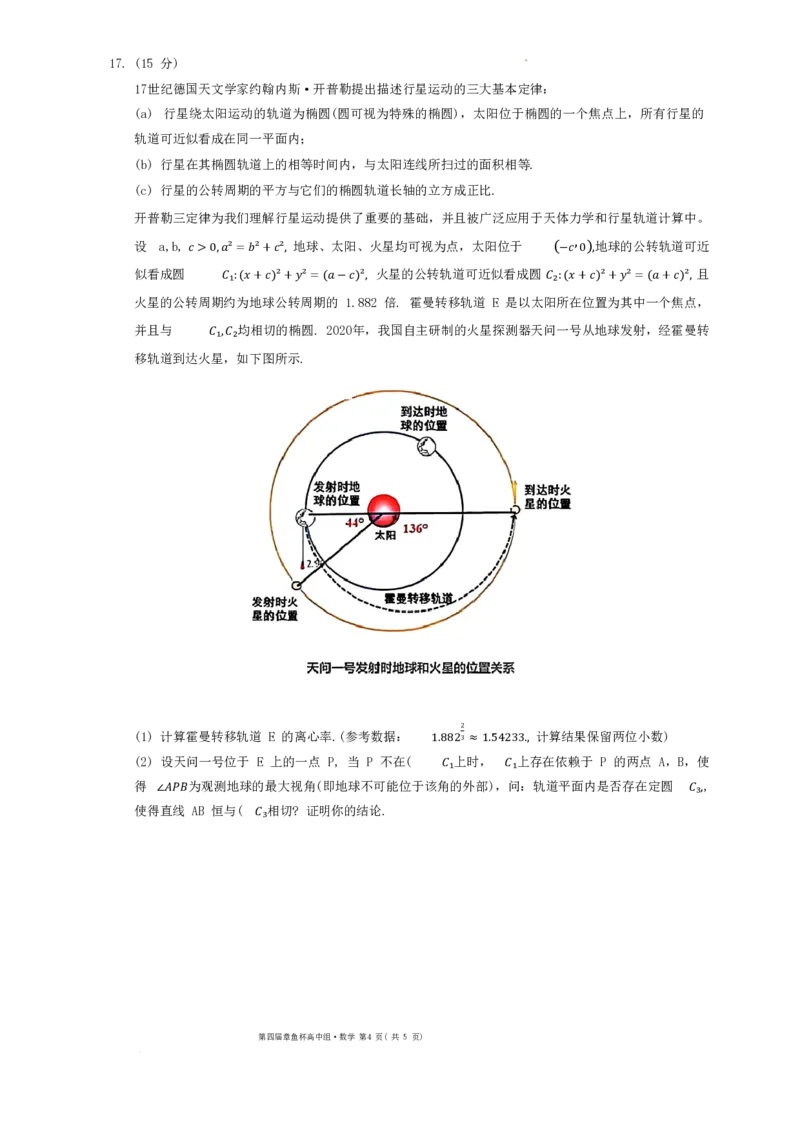
并且与 均相切的椭圆. 2020年,我国自主研制的火星探测器天问一号从地球发射,经霍曼转
移轨道到达火𝐶𝐶星₁,,𝐶𝐶₂如下图所示.
(1) 计算霍曼转移轨道 E 的离心率.(参考数据: 计算结果保留两位小数)
2
(2) 设天问一号位于 E 上的一点 P, 当 P 不在( 1 .88上2
3
时≈,1.5 4 23上3.,存在依赖于 P 的两点 A,B,使
得 为观测地球的最大视角(即地球不可能位于该角𝐶𝐶₁的外部),𝐶𝐶问₁:轨道平面内是否存在定圆 ,
使得∠直𝑂𝑂𝑃𝑃线𝑂𝑂 AB 恒与( 相切? 证明你的结论. 𝐶𝐶₃,
𝐶𝐶₃
第四届章鱼杯高中组·数学 第4 页( 共 5 页)
学科网(北京)股份有限公司18. (17 分)
设
2ln𝑥𝑥+1 𝑎𝑎𝑥𝑥
(1) 若𝑓𝑓( 𝑙𝑙) = 𝑥𝑥,讨−论𝑙𝑙𝑒𝑒 f(,x𝑎𝑎)∈ 的𝑅𝑅.单调性;
(2) 若 𝑎𝑎=0,, 求 f(x) 的最大值(用 a 表示);
(3) 若 f(𝑎𝑎x)≥ 恰0,有三个极值点,直接写出 a 的取值范围.
19. (17 分)
数列 满足 且 构成等差数列.
(1) 试求{出
𝑎𝑎𝑙𝑙
所}
𝑙𝑙
有
∈𝑁𝑁
三元实数组
𝑎𝑎₀ =
(α
𝛼𝛼,
,
𝑎𝑎
β
₁=
,γ
𝛽𝛽,
)
𝑎𝑎
,
₂ =
使
𝛾𝛾
得
, ∀ 𝑙𝑙 ≥ 3 ,𝑎𝑎ₙ ₋₃,
为
𝑎𝑎ₙ
等
₋₁𝑎𝑎
比
ₙ₋
数
₂,𝑎𝑎
列
ₙ
.
(2) 若 求 的通项公式.
𝑎𝑎ₙ
(
𝛼𝛼,𝛽𝛽,𝛾𝛾
)
=
(
1,2,2
)
, 𝑎𝑎ₙ
第四届章鱼杯高中组·数学 第5 页( 共 5 页)
学科网(北京)股份有限公司第四届章鱼杯高中组解答
大章鱼 OctoPus
2024 年 2 月 6 日
1.【答案】B
【解析】原方程等价于x²-x-2024=0(x>0,x≠1), 显然只有一个实根.
2.【答案】C
【解析】熟知3+4i的辐角θ∈(53°,54°), 而 53×6=318>270,54×5=270,故5θ<
270°,6θ>270°, 所以nmin = 6.
3.【答案】B
【解析】由 f(0)=0,f'(0) = 3 可设 于是 由
′
f(1)=1 知a+b=-2, 由 f'(1)=9 知3a+2𝑓𝑓b(=𝑙𝑙6),= 联𝑎𝑎𝑙𝑙立³解+𝑏𝑏得𝑙𝑙 ²a+=130𝑙𝑙,b=-12,𝑓𝑓 ( 𝑙𝑙 ) = 3 𝑎𝑎 𝑙𝑙 ² + 2 𝑏𝑏 𝑙𝑙 + 于3.是
故.
4.【
𝑓𝑓(
答
𝑙𝑙)
案
=
】
1
A
0 𝑙𝑙³−12𝑙𝑙²+3𝑙𝑙, 𝑓𝑓(3)=10×3³−12×3²+3×3=171
【解析】设 P,Q,R 分别为使得 p,q,r 为真命题的取值集合, 依题意得 P 是 Q 的真子集, P
是 R的真子集, 从而 P 是 Q∪R的真子集, 故p是q∨r的充分不必要条件, A 正确, D 错误. 又
P Q∩R, 故C 错误. 注意到 P 可能恰为Q∩R, 此时p是q∧r的充要条件,故 B 错误.
5.【
⊆
答案】D
【解析】设 M 为 AB 中点, 注意到
2
(2𝑥𝑥𝐴𝐴−𝑦𝑦𝐴𝐴)+(2𝑥𝑥𝐵𝐵−𝑦𝑦𝐵𝐵) −ln𝑥𝑥𝐴𝐴+𝑥𝑥𝐴𝐴−𝑥𝑥𝐴𝐴−2
2𝑙𝑙𝑀𝑀−𝑦𝑦𝑀𝑀 = 2 = 2
2 2
1−𝑥𝑥𝐴𝐴+𝑥𝑥𝐴𝐴−𝑥𝑥𝐴𝐴+4 (𝑥𝑥𝐴𝐴−1)
于是
≥ 2 = 2 +2≥2
2√5 2 2 2 2 2√5 4√5
|𝑂𝑂����𝑂𝑂�⃗+𝑂𝑂����𝑂𝑂�⃗|=2|�𝑂𝑂���𝑂𝑂��⃗|= 5 �𝑙𝑙𝑀𝑀+𝑦𝑦𝑀𝑀√2 +1 ≥ 5 |2𝑙𝑙𝑀𝑀−𝑦𝑦𝑀𝑀|≥ 5 .
当 A(1,1),B(0.6,-1.8) 时等号成立, 所以所求最小值为
4√5
5 .
1
学科网(北京)股份有限公司6.【答案】C
【解析】不妨设出发顺序为 1,2,…,n, 若 1≤i≤n-1, 使得 交换i 与
i+1 的出发顺序,显然 i +1 会比交换前更早完成比赛. 交换前 i 和i+1 的完赛总时长为
∃ 𝑏𝑏ᵢ+𝑟𝑟ᵢ<𝑏𝑏ᵢ₊₁+𝑟𝑟ᵢ₊₁ ,
交换后 i 和i+1的完赛总时长为 又 故交换后 i
𝑠𝑠ᵢ+𝑠𝑠ᵢ₊₁+
和 i+1的完赛总时长减少,而其他人不变,从而全体完赛总时长减少. 由此可反复交换在此过程中完赛
𝑏𝑏ᵢ₊₁+𝑟𝑟ᵢ₊₁, 𝑠𝑠ᵢ₊₁+𝑠𝑠ᵢ+𝑏𝑏ᵢ+𝑟𝑟ᵢ, 𝑏𝑏ᵢ+𝑟𝑟ᵢ<𝑏𝑏ᵢ₊₁+𝑟𝑟ᵢ₊₁,
总时长均减小,直到按 降序排列,此时达到最优.
7.【答案】A
𝑏𝑏ᵢ+𝑟𝑟ᵢ
【解析】若0≤k≤2, 则 -1≤1-k≤1, 取y=0, 则 cosx+kcosy=1 有解, 不符题意, 舍去.若k<0, 则1-
kcosy=cosx≤1, 于是 kcosy≥0,结合k<0知cosy≤0,故 取 即可. 若 k >2, 则
𝜋𝜋 𝜋𝜋
故 取 即可.| 𝑦𝑦综|≥上2,, k 的𝑚𝑚范=围2是( (-∞,0)∪(2,+∞). cos𝑦𝑦=
1−cos𝑥𝑥 2 2 2
8.【答
𝑘𝑘
案】
≤
C
𝑘𝑘 <1, |𝑦𝑦|≥arccos𝑘𝑘, 𝑚𝑚=arccos𝑘𝑘
【解析】设接 n条线, 1≤k≤n,第k条线的接法数为 又因为平均分成 n组,故总的接法
2
数为 ∀设n= no时an最大, 其中1≤n₀≤13. 若𝐶𝐶12≤8−n2₀𝑘𝑘,≤12,则 置
𝑙𝑙 2
∏ 𝑘𝑘=1𝐶𝐶28−2𝑘𝑘
𝑎𝑎𝑙𝑙 = 𝑙𝑙! . 𝑎𝑎𝑙𝑙0−1 ≤ 𝑎𝑎𝑙𝑙0 ≥ 𝑎𝑎𝑙𝑙0+1,
𝑙𝑙 2 2 2
𝑎𝑎𝑙𝑙+1 ∏ 𝑘𝑘=1𝐶𝐶2𝑠𝑠−2𝑘𝑘 𝐶𝐶2𝑠𝑠−2𝑙𝑙−2 𝑙𝑙! 𝐶𝐶26−2𝑙𝑙 13−𝑙𝑙 25−2𝑙𝑙
( ) ( )( )
则 n 𝑏𝑏 o 𝑙𝑙 = = mi𝑎𝑎𝑙𝑙n{ = n∈[1
(
,𝑙𝑙1+12
)
]𝑙𝑙!∩Z|b ⋅ n∏ <𝑘𝑘 𝑙𝑙 1=1}𝐶𝐶2 2 ,8− 2𝑘𝑘 = 𝑙𝑙+1 解 = 得 n𝑙𝑙+₀1=11.若 no= 13, 同理可得 a₁₃ 2024, 符合要求.
15.(1) 解:设每个五棱锥的高为 h,拼接面与双五棱锥的交集为正五边形,其外接圆半径为 故
1
∘
(3 分)
𝑅𝑅=2sin36 , ℎ=
2
�50−10√5
√1−𝑅𝑅 = 10 .
又底面正五边形的面积为 1 0所以双五棱锥的体积为
5 ∘
4tan54 ,
1 5 ∘ �50−10√5 5+√5
𝑉𝑉 =2×3×4tan54 × 10 = 12 .
(6分)
显然双五棱锥的表面积为
√3 5√3
∑𝑆𝑆=10× 4 = 2 .
(8 分)
故内切球半径为
3𝑉𝑉 5√3+√15
𝑟𝑟=∑𝑆𝑆= 30 . (10 分)
(2) 解:所求二面角为侧面正三角形与拼接面构成的锐二面角(记为θ) 的两倍.
显然 于是所求二面角的余弦值为
ℎ
tan𝜃𝜃=1 2tan54 ∘ =3−√5.
2
1−tan 𝜃𝜃 4√5−5
cos2𝜃𝜃 =1+tan 2 𝜃𝜃 = 15 . (13 分)
5
学科网(北京)股份有限公司16. (1) 解: 我们考虑更一般的情形:
求倒数第 k 轮开始前剩下的选手恰好为 x₁,x₂,……,x₂k的概率.
要实现这一点,这 k名选手是种子选手,即在前面的比赛中两两不能相遇,而且必须在其全部 场比赛中获
胜. (4 分)
2ᵏ(𝑙𝑙−𝑘𝑘)
锦标赛树形的2ⁿ片树叶的填写方式有(2ⁿ)!种,为使其称为种子,我们有 种方式放置
−
𝑘𝑘 𝑙𝑙−𝑘𝑘 2
最上面的2个选手,且有( 种方式放置其他选手,因此其概率为 (
2
)
!
( 2
2
𝑝𝑝 2∗ ( ) 𝑙𝑙−𝑘𝑘) 特别地,本
( )
( 2ⁿ−2ᵏ ) ! 𝐶𝐶 2 2 𝑘𝑘 𝑙𝑙 .
题为 k=1 的情形,故所求概率为 (7分)
2 𝑙𝑙−1
2𝑝𝑝
( )
(2) 证明:x; 为总冠军的概率是 x; 为总冠军的2所 𝑙𝑙 −有1 . 种可能的比赛结果的概率之和.在所有这
些结果中将x与x+1 交换. 对于某一特定的比赛结果, 若x 2ⁿ−1 !与xi+1 从未在比赛中相遇,则无影响,
( )
否则改变后的这一特定比赛结果的概率等于用 乘以改变前这一结果发生的概率.
ᵢ ᵢ ᵢ
1−𝑝𝑝
(10 分) 𝑝𝑝
注意到 因此求和后总概率变小, 这表明x 为总冠军的概率大于x+₁为总冠军的概率.
1−𝑝𝑝
(15 分)
𝑝𝑝 <1, ᵢ ᵢ
17.(1) 解:设 T₁,T₂分别为地球、火星的公转周期. 由开普勒第三定律得
3 2
𝑎𝑎−𝑐𝑐 𝑇𝑇1
�𝑎𝑎+𝑐𝑐� = �𝑇𝑇2� (2 分)
于是
𝑇𝑇2 3
𝑐𝑐
�𝑇𝑇1 � −1
1.54233−1
𝑒𝑒 = 𝑎𝑎 =
�
𝑇𝑇
𝑇𝑇
2
1 �
3
+1
≈ 1.54233+1 ≈ 0.21. (4 分)
(2) 存在.
证明:设 P(x₀,y₀), A(x₁,y₁), B(x₂,y₂).
由 PA 与C₁相切可知, 直线 PA 的方程为 (6 分)
2
由 PB 与C₁相切可知, 直线 PB 的方程为 ( 𝑙𝑙+𝑐𝑐 )( 𝑙𝑙1+𝑐𝑐 ) +𝑦𝑦1𝑦𝑦 = ( 𝑎𝑎−𝑐𝑐 ) . ( ⋆1 ) (8 分)
2
考虑直线 由((𝑙𝑙*1+),𝑐𝑐()*(2𝑙𝑙) 2+知A𝑐𝑐 ),B+ 都𝑦𝑦2在𝑦𝑦这=条( 𝑎𝑎直−线𝑐𝑐上) .,( ⋆所2以)它就是直线 AB.
(10 分) 𝑙𝑙+𝑐𝑐 𝑙𝑙₀+𝑐𝑐 +𝑦𝑦₀𝑦𝑦 = 𝑎𝑎−𝑐𝑐 ²,
( )( ) ( )
6
学科网(北京)股份有限公司取 则 AB 到 J 的距离为
2𝑎𝑎𝑐𝑐
𝐽𝐽�−𝑎𝑎+𝑐𝑐,0�,
−2𝑎𝑎𝑎𝑎(𝑥𝑥0+𝑎𝑎) 2
| 𝑎𝑎+𝑎𝑎 +𝑐𝑐𝑥𝑥0+2𝑎𝑎𝑐𝑐−𝑎𝑎 |
𝑑𝑑(𝑂𝑂𝑂𝑂 , 𝐽𝐽) = 2 2
�(𝑥𝑥0+𝑐𝑐) +𝑦𝑦0
2 3
|(𝑐𝑐−𝑎𝑎𝑐𝑐)𝑥𝑥0+𝑎𝑎 𝑐𝑐−𝑎𝑎 |
𝑎𝑎
= (𝑎𝑎+𝑐𝑐)�𝑎𝑎+𝑎𝑎𝑥𝑥0�
𝑎𝑎(𝑎𝑎−𝑐𝑐)
= 𝑎𝑎+𝑐𝑐 .
故 AB 始终与圆 相切. (15 分)
2 2
2𝑎𝑎𝑐𝑐 2 𝑎𝑎 ( 𝑎𝑎−𝑐𝑐 )
𝐶𝐶3: � 𝑙𝑙+𝑎𝑎+𝑐𝑐� +𝑦𝑦 = � 𝑎𝑎+𝑐𝑐 �
18. (1) 解: a=0 时, (2 分)
2
2ln𝑥𝑥+1 ′ 1−2ln𝑥𝑥−𝑥𝑥
𝑓𝑓(𝑙𝑙)= 𝑥𝑥 −𝑙𝑙,𝑓𝑓(𝑙𝑙)= 𝑥𝑥 2 .
置 则 于是 φ(x) 在(0,+∞) 单调递减.
2
′ −2 ( 𝑙𝑙+1 )
又φ(𝜙𝜙1()𝑙𝑙=)0=, 故1−0<2x𝑙𝑙<𝑙𝑙1𝑙𝑙时−φ𝑙𝑙²(,x)>0, 𝜑𝜑x>
(
1𝑙𝑙时
)
φ=(x)<0𝑙𝑙. < 0, (4 分)
从而 f(x) 在(0,1) 单调递增, 在(1,+∞) 单调递减. (5 分)
(2) 解: 置: g(x) =2lnx+1, h(x) =x(xe-a), (6 分)
ˣ
则
′ 2 ′ 𝑎𝑎𝑙𝑙 2 𝑎𝑎𝑙𝑙
𝑔𝑔
(
𝑙𝑙
)
=𝑙𝑙,ℎ
(
𝑙𝑙
)
= 2𝑙𝑙𝑒𝑒 −𝑎𝑎+𝑎𝑎𝑙𝑙 𝑒𝑒
由 知
′ 2
x₀>𝑔𝑔0,′
(
𝑙𝑙x
)
>0=, − g𝑙𝑙(2x)<≤0g'(x₀)(x-x₀)+g(x₀). (7 分)
∀由 ∀
′
ℎ′(𝑙𝑙) =2(𝑒𝑒ᵃˣ+𝑎𝑎𝑙𝑙𝑒𝑒ᵃˣ)+𝑎𝑎(2𝑙𝑙𝑒𝑒ᵃˣ+ 𝑎𝑎 𝑙𝑙 ²𝑒𝑒 ᵃ ˣ) > ( (8 分)
′
由𝜙𝜙a𝑙𝑙>₀0知>,0 ,存∀𝑙𝑙在>唯0一,ℎ的(𝑙𝑙x)₀≥>0ℎ, (使𝑙𝑙₀)得(𝑙𝑙( − 𝑙𝑙 ₀) + ℎ ( 𝑙𝑙₀ ). 注意到
𝑎𝑎𝑙𝑙₀+2𝑙𝑙𝑙𝑙𝑙𝑙₀=0.
𝑎𝑎𝑥𝑥0
𝑔𝑔(𝑙𝑙0)−ℎ(𝑙𝑙0) =2ln𝑙𝑙0+1−𝑙𝑙0(𝑙𝑙0𝑒𝑒 −𝑎𝑎 )
2 𝑎𝑎𝑥𝑥0
=2ln𝑙𝑙0+1+𝑎𝑎𝑙𝑙0 −𝑙𝑙0𝑒𝑒
𝑎𝑎𝑥𝑥0+2ln𝑥𝑥0
=1=-1 1−𝑒𝑒
=0
(9 分)
7
学科网(北京)股份有限公司
) 知又注意到
′ ′ 2 𝑎𝑎𝑙𝑙0 2 𝑎𝑎𝑙𝑙0
𝑔𝑔(𝑙𝑙0 )−ℎ(𝑙𝑙0
)
=𝑙𝑙0−2𝑙𝑙0𝑒𝑒 −𝑎𝑎+𝑎𝑎𝑙𝑙0𝑒𝑒
2�1−𝑒𝑒
𝑎𝑎𝑥𝑥0+2ln𝑥𝑥0�
𝑎𝑎𝑥𝑥0+2ln𝑥𝑥0
=0=-a+a 𝑥𝑥0 −𝑎𝑎+𝑎𝑎𝑒𝑒
=0
(10 分)
所以 x>0, 我们有
∀
′ ′
𝑔𝑔(𝑙𝑙)≤𝑔𝑔 (𝑙𝑙₀)(𝑙𝑙−𝑙𝑙₀)+𝑔𝑔(𝑙𝑙₀)=ℎ (𝑙𝑙₀)(𝑙𝑙−𝑙𝑙₀)+ℎ(𝑙𝑙₀)≤ℎ(𝑙𝑙) (12 分)
即 整理得 f(x)≤-a, 且等号在 ax+2lnx=0 时取到.
故 f(x) 的最大值为 -a. (13 分)
2𝑙𝑙𝑙𝑙𝑙𝑙+1 ≤ 𝑙𝑙(𝑙𝑙𝑒𝑒ᵃˣ−𝑎𝑎),
(3) 当 f(x) 有三个极值点时, a 的取值范围是 (17 分)
2
�
−𝑒𝑒,0
�
.
19.(1) 解: 依题意得 (2 分)
设 则 𝑎𝑎ₙ=2𝑎𝑎ₙ₋₁𝑎𝑎ₙ₋₂−𝑎𝑎ₙ₋₃. (4 分)
又q≠ 𝑎𝑎ₙ 0 = ,则 𝑎𝑎₀ ( 𝑞𝑞 ⁿ, ∀𝑙𝑙≥3,𝑎𝑎0𝑞𝑞
𝑒𝑒
=2 𝑎𝑎 从0
2
𝑞𝑞 而
2𝑒𝑒
q
−
ⁿ
3
− 为 𝑎𝑎 常0𝑞𝑞 数
𝑒𝑒−
,
3
. 由n的任意性知 q =1, 于是 又由于
3 2 𝑙𝑙 2
等比数列中不能𝑎𝑎0有𝑞𝑞 =0,2 𝑎𝑎0故𝑞𝑞 −a₀𝑎𝑎=0 , 1, 于是(α,β,γ)=(1,1,1), 此时an恒为 1, 满𝑎𝑎足0等=比2𝑎𝑎数0−列𝑎𝑎的0.要求.
(6 分)
(2) 解: 记 (8 分)
1+√5 1−√5 √5 𝑒𝑒 𝑒𝑒
注意到r,s是关𝑝𝑝=于2x的+√一3元,𝑞𝑞二=次2−方√程3, 𝑟𝑟 = 2 ,𝑠𝑠 = 2 ,𝐹𝐹𝑒𝑒的=两5根(𝑟𝑟,−故𝑠𝑠 ).
𝑙𝑙²=𝑙𝑙+1
√ 5 𝑙𝑙−1 𝑙𝑙−1 𝑙𝑙−2 𝑙𝑙−2 √ 5 𝑙𝑙−2 𝑙𝑙−2 √ 5 𝑙𝑙 𝑙𝑙
𝐹𝐹𝑙𝑙−1+𝐹𝐹𝑙𝑙−2 = 5 (𝑟𝑟 −𝑠𝑠 +𝑟𝑟 −𝑠𝑠 )= 5 � 𝑟𝑟 (1+𝑟𝑟)−𝑠𝑠 (1+𝑠𝑠)� = 5 (𝑟𝑟 −𝑠𝑠 (1)0 = 分 𝐹𝐹 ) 𝑙𝑙 .
下面归纳证明: (12 分)
𝐹𝐹𝑙𝑙 𝐹𝐹𝑙𝑙
𝑝𝑝 +𝑞𝑞
n =0,1,2时, 结论显𝑎𝑎然𝑙𝑙 =成立.2
对n≥3,假设结论对 n - 1,n -2,n - 3 成立,
8
学科网(北京)股份有限公司注意到 故
𝑝𝑝+𝑞𝑞=4,𝑝𝑝𝑞𝑞=1,
𝑎𝑎ₙ=2𝑎𝑎ₙ₋₁𝑎𝑎ₙ₋₂−𝑎𝑎ₙ₋₃
1 𝐹𝐹𝑛𝑛−1 𝐹𝐹𝑛𝑛−1 𝐹𝐹𝑛𝑛−2 𝐹𝐹𝑛𝑛−2 1 𝐹𝐹𝑛𝑛−3 𝐹𝐹𝑛𝑛−3
=2(𝑝𝑝 +𝑞𝑞 )(𝑝𝑝 +𝑞𝑞 )−2(𝑝𝑝 +𝑞𝑞 )
1 𝐹𝐹∗ 𝐹𝐹𝑛𝑛 𝐹𝐹𝑛𝑛−1−𝐹𝐹𝑛𝑛−2 𝐹𝐹𝑛𝑛−2 𝐹𝐹𝑛𝑛−1−𝐹𝐹𝑛𝑛−2 𝐹𝐹𝑛𝑛−2 𝐹𝐹𝑛𝑛−2 1 𝐹𝐹𝑛𝑛−3 𝐹𝐹𝑛𝑛−3
= 2(𝑝𝑝 +𝑞𝑞 +𝑝𝑝 𝑝𝑝 +𝑞𝑞 𝑝𝑝 𝑞𝑞 )−2(𝑝𝑝 +𝑞𝑞 ,
1 𝐹𝐹𝑛𝑛 𝐹𝐹𝑛𝑛
从而结论
=
对
2
n也
(𝑝𝑝
成立
+
,完
𝑞𝑞
成归
).
纳.
综上, 1 √ 𝑄𝑄 7 𝑙𝑙 1+ 5 𝑙𝑙 √ 5 5 1+ 5 𝑙𝑙 1+ 𝜉𝜉 𝑙𝑙
√ √ √
𝑎𝑎𝑙𝑙 = 2 2+ 3 1+ 𝑙𝑙}2 − 2 }+ 2− 3 2 − 2
�� √ � �� √ � � � � � √ � �� � � � ��
(17 分)
学科网(北京)股份有限公司