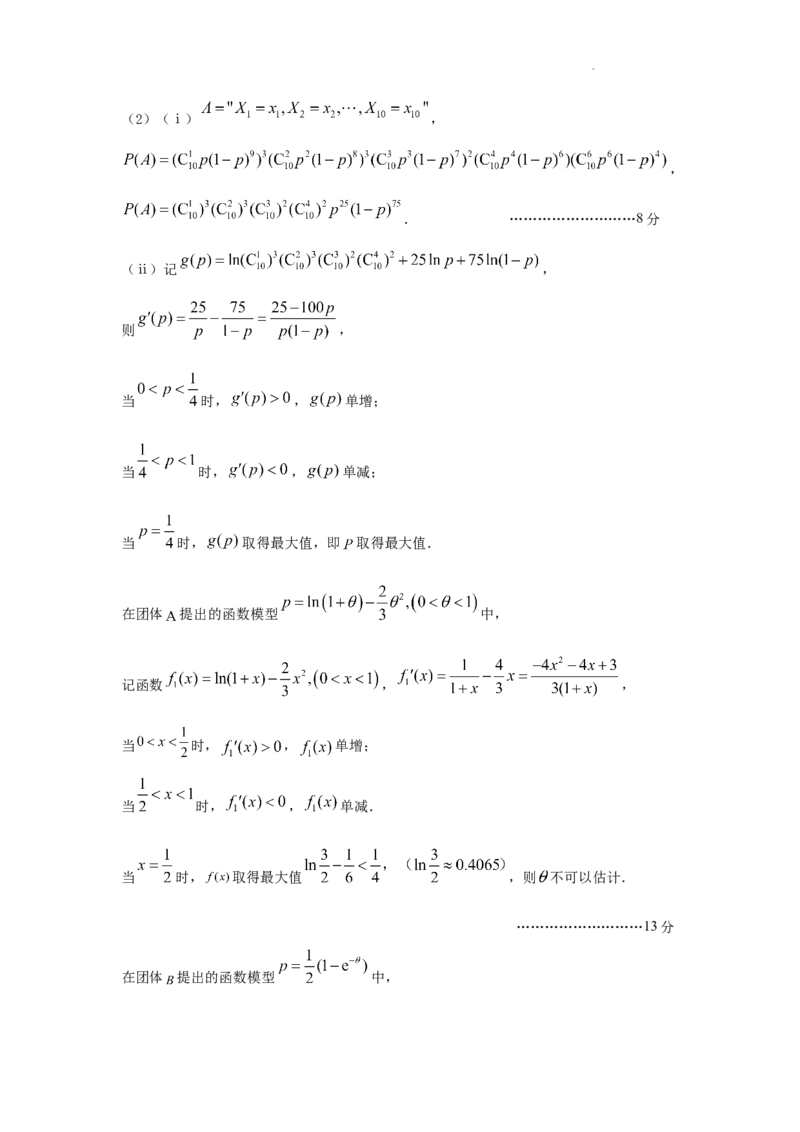文档内容
2023-2024 学年度东北育才学校高中部高三年级第六次模拟
考试暨假期质量测试数学科答案
一.单选题
1. A 2.B 3.B 4.A 5.C 6.D 7.D 8.A
二.多选题
9. AD 10.BCD 11.AC
三.填空题
12. 13. 14.
四.解答题
15.(本题满分13分)
解:(1)设等差数列 的公差为 ,等比数列 的公比为 ,
则 , , , …………………………3
分
又 , 可得 , …………………………4分
所以 . …………………………6
分
(2)由(1)可得 , …………………………7分
故 ,以它为通项的数列是以 为首项、公比为 的等比数列,……8分
所以数列 的前2n项和 …………10分
. ………………………13分
16.(15分)
解(1)取 中点 ,由题意, ,
又 ,故 .
又 ,故 ,
学科网(北京)股份有限公司所以四边形 为平行四边形,则 .
由 平面 ,故 平面 ,
又 面 ,故平面 平面 .…………………………7分
(2)以 为坐标原点, 的方向为 轴的正方向,建立如图所示的空
间直角坐标系.则有:
,
故
设平面 的法向量
而 ,
故 ,令 ,得
设所求角的大小为 ,则 .
所以直线 与平面 所成角的正弦值为 . ………………………15分
17.(1)由题知,随机变量 服从二项分布, ,
由 ,即 ,
得 ,所以 . ………………………4分
学科网(北京)股份有限公司(2)(ⅰ) ,
,
. ………………………8分
(ⅱ)记 ,
则 ,
当 时, , 单增;
当 时, , 单减;
当 时, 取得最大值,即 取得最大值.
在团体 提出的函数模型 中,
记函数 , ,
当 时, , 单增;
当 时, , 单减.
当 时, 取得最大值 ,则 不可以估计.
………………………13分
在团体 提出的函数模型 中,
学科网(北京)股份有限公司记函数 , 单调递增,
令 ,解得 ,
则 是 的最大似然估计. ………………………15分
18.解:(1)由已知
联立直线 得
设 ,则
所以
联立直线 得
设 ,则
所以
因为 ,所以 …………………………4分
(2)因为 ,所以 的直线方程为
,因为 过点
整理得 ,
所以 ①
……………………7分
同理可得 ②
学科网(北京)股份有限公司同理可得AC: ,BD:
联立 与 方程,解出点 坐标,
, …………………………11
分
由①②得 , 带入点 纵坐标
所以点 坐标在直线 上 ………………………17分
19.(1)由题意得,函数 的定义域为 .
由 得: ,
当 时, 在 上单调递增;
当 时,由 得 ,由 得 ,
所以 在 上单调递增,在 上单调递减.……………………4分
(2)因为 是方程 的两不等实根,
学科网(北京)股份有限公司即 是方程 的两不等实根,
令 ,则 ,
即 是方程 的两不等实根.
令 ,则 ,
所以 在 上递增,在 上递减, ,
当 时, ;当 时, 且 .
所以 ,即 .
令 .
(i)要证 ,只需证 , ……………………6分
解法1:令 ,
则 ,
令 ,
则
,
所以 在 上递增, ,
学科网(北京)股份有限公司所以 ,所以 ,
所以 ,
所以 ,即 ,所以 . ……………………11分
解法2:先证 ,
令 ,只需证 ,
只需证 ,
令 ,
,
在
所以 上单调递减,所以 .
因为 ,所以 ,
所以 ,即 ,
所以 .
解法3:由 ,
设 ,
所以 ,
学科网(北京)股份有限公司即 ,
构造函数 ,
,
所以 在 上单调递增,所以 .
(ii)要证: ,只需证: ,
只需证: ,
只需证: ,
只需证: ,
令 得
即 ①
令 得
即 ②
学科网(北京)股份有限公司①+②得: ,
即 . ……………………17分
学科网(北京)股份有限公司