河南鹤壁高中2025届高三上学期第一次综合检测（7月）数学试题+答案(1)_8月_240804河南鹤壁高中2025届高三上学期第一次综合检测（7月）

2025 学年鹤壁市高中高三（上）第一次综合检测 数学试题 注意事项： 1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。 2.每道选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净 后，再选涂其他答案标号。在试题卷上作答无效。 3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需 改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无 效。 4.考试结束后，请将本试卷和答题卡一并交回。 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 1.已知 a，b∈R，若 4a2+b2 ⋅ a2+4b2 的最大值为 m，且不等式x2−ax+b<0的解集为(1,2m)，则 a2+b2 a+b=（ ） A.3 B.43 C.7 D.11 2.设a=log 0.5,b=0.3−0.4,c=0.5−0.4，则a,b,c的大小关系是（ ） 0.4 A.b>c>a B.c>b>a C.b>a>c D.c>a>b 3.已知 A，B，C，D四点均在半径为R（R为常数）的球O的球面上运动，且 4 AB= AC,AB⊥ AC,AD⊥BC，若四面体 ABCD的体积的最大值为 ，则球 O的表面积为（ ） 3 9π A.2π B.3π C. D.9π 4  π x 4.当 x∈ 0,  时，asin2x≥2sin 1−sinx恒成立，则实数a的取值范围为（ ）  2 2 A.(0,1 ] B.  0, 2−1  C.  2−1,+∞ ) D.   1 ,+∞  2  5.设 z ， z 是复数，则下列命题中是假命题的是（ ） 1 2 A.若 z=z ⋅z ，则|z|=|z |⋅|z | B.若 z=z ⋅z ，则 z =z ⋅z 1 2 1 2 1 2 1 2 C.若|z |=|z |，则z2 =z2 D.若|z |=|z |，则z ⋅z =z ⋅z 1 2 1 2 1 2 1 1 2 2 高三（上）第一次综合检测-数学试题 第 1 页（共 17 页） 学科网（北京）股份有限公司3 6.重庆八中味园食堂午餐情况监测数据表明，小唐同学周一去味园的概率为 ，周二去味园的概 5 3 率为 ，且小唐周一不去味园的条件下周二去味园的概率是周一去味园的条件下周二去味园的 10 概率的 2 倍，则小唐同学周一、周二都去味园的概率为（ ） 9 9 3 3 A. B. C. D. 70 50 40 14 7.在长方体 ABCD−ABCD 中， AB=2AD=2AA，点M 是线段CD 上靠近D 的四等分点，点 N 是 1 1 1 1 1 1 1 1 线段CC 的中点，则平面 AMN截该长方体所得的截面图形为（ ） 1 A.三角形 B.四边形 C.五边形 D.六边形 8.已知函数 f(x)的导函数为 f′(x)，记 f (x)= f′(x)， f (x)= f ′(x), 1 2 1 f (x)= f′(x)( n∈N∗) .若 f(x)=xsinx，则 f (x)+ f (x)=（ ） n+1 n 2019 2021 A.−2cosx B.−2sinx C.2cosx D.2sinx 二、多项选择题：本题共３小题，每小题６分，共 18 分.在每小题给出的选项中，有多项符 合题目要求.全部选对的得 6 分，有选错的得 0 分，若只有 2 个正确选项，每选对 1 个得 3 分；若只有 3个正确选项，每选对 1个得 2分. x sin2x 9.已知函数 f (x)= − ，则（ ） 2 1+cos2x A.函数 f (x)一个周期是π  π π B.函数 f (x)递减区间为kπ− ,kπ+  (k∈Z)  2 2 C.函数 f (x)有无数多个对称中心 D.过点(2,0)作曲线 y= f (x)的切线有且只有一条 π 10.已知函数 f (x)的图象是由函数 y=2sinxcosx的图象向右平移 个单位得到，则（ ） 6 A. f (x)的最小正周期为 π  π π B. f (x)在区间 − , 上单调递增    6 3 C. f (x)的图象关于直线x= π 对称 3 π  D. f (x)的图象关于点 ,0对称 6  11.在三棱锥P−ABC中，PA⊥平面 ABC,AB⊥BC,AB=BC =2,PA=2 3，点D是三角形PAB内的动 点（含边界）， AD⊥CD，则下列结论正确的是（ ） π A.PB与平面 ABC所成角的大小为 3 B.三棱锥C−ABD的体积最大值是 2 高三（上）第一次综合检测-数学试题 第 2 页（共 17 页） 学科网（北京）股份有限公司2π C.D点的轨迹长度是 3 5 2 D.异面直线CD与 AB所成角的余弦值范围是[ , ) 10 2 三、填空题：本大题共 3个小题，每小题5分，共 15 分. 12.对于函数 f (x)= cosx −kx(x≥0)，当该函数恰有两个零点时，设两个零点中最大值为α，当该 ( 1+α2) sin2α ( 1+β2) cos2β 函数恰有四个零点时，设这四个零点中最大值为β，求 + = . 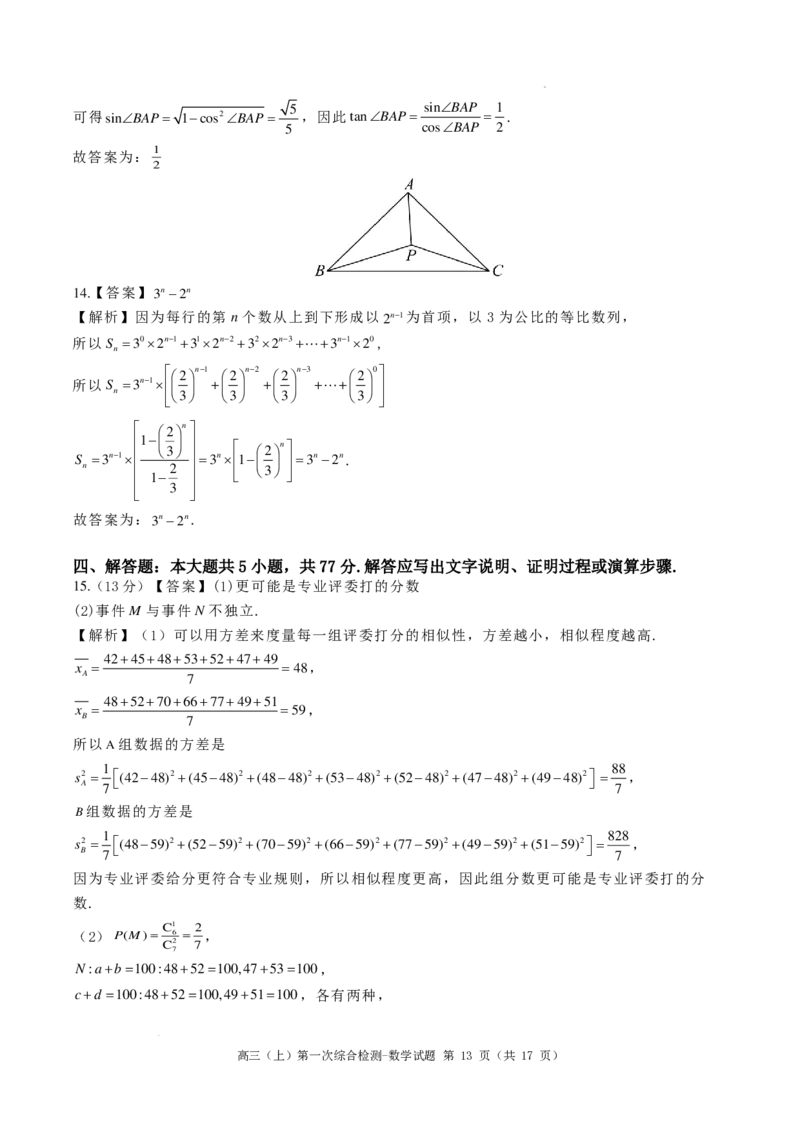α 1−β2 13.已知P是ABC内一点，∠ABP=45°,∠PBC =∠PCB=∠ACP=30°，则tan∠BAP= . 14.下图数阵的每一行最右边数据从上到下形成以 1 为首项，以 2 为公比的等比数列，每行的第n 个数从上到下形成以2n−1为首项，以 3 为公比的等比数列，则该数阵第n行 ( n∈N*) 所有数据的和 S = . n 四、解答题：本大题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤. 15.（13分）在某项比赛中，7 位专业评委和 7 位观众评委分别给选手打分.针对某位选手，下面 是两组评委的打分： A组 42 45 48 53 52 47 49 B组 48 52 70 66 77 49 51 (1)选择一个可以度量每一组评分相似性的量，据此判断哪一组分数更可能是专业评委打的分 数； (2)现从 A组评委所打分数中随机抽取 2 个分数，记为a，b，从B组评委所打分数中随机抽取 2 个分数，记为c，d.记事件M :a，b中有一个数据为 48，事件 N:a+b=100或c+d =100，判断事 件M 与事件N 是否相互独立. 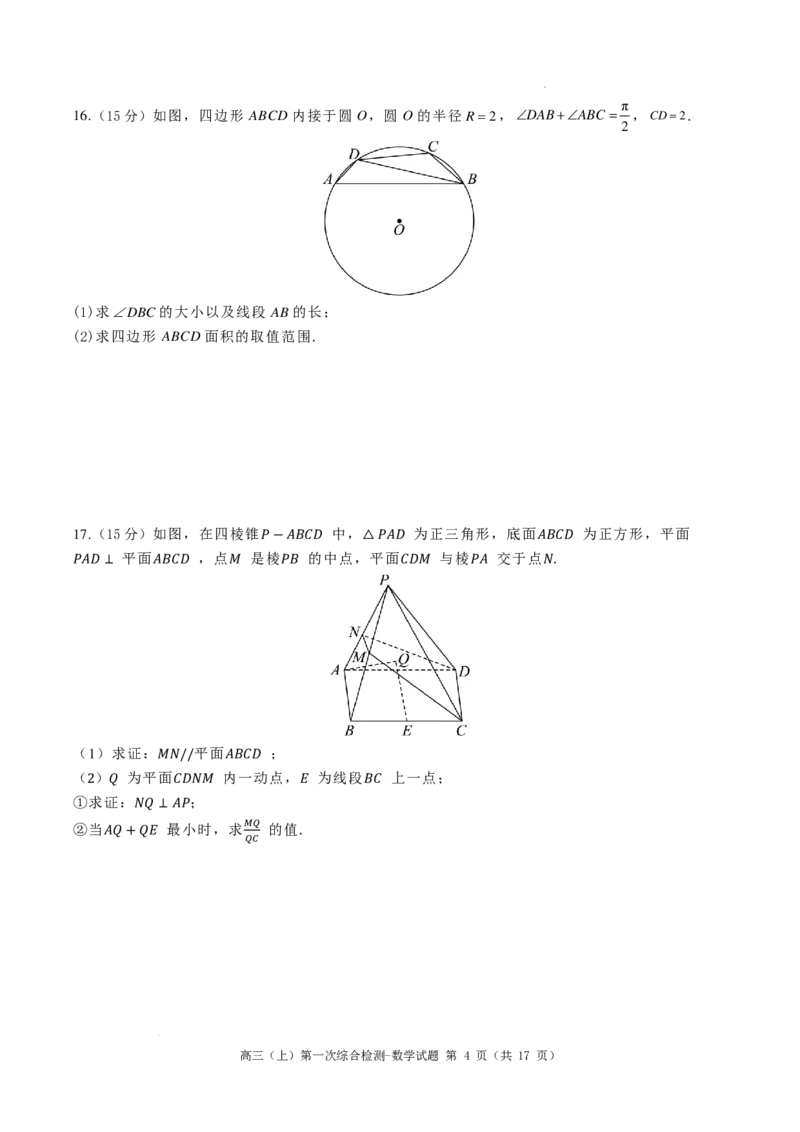高三（上）第一次综合检测-数学试题 第 3 页（共 17 页） 学科网（北京）股份有限公司π 16.（15分）如图，四边形 ABCD内接于圆 O，圆 O的半径R=2，∠DAB+∠ABC = ，CD=2. 2 (1)求∠DBC的大小以及线段 AB的长； (2)求四边形 ABCD面积的取值范围. 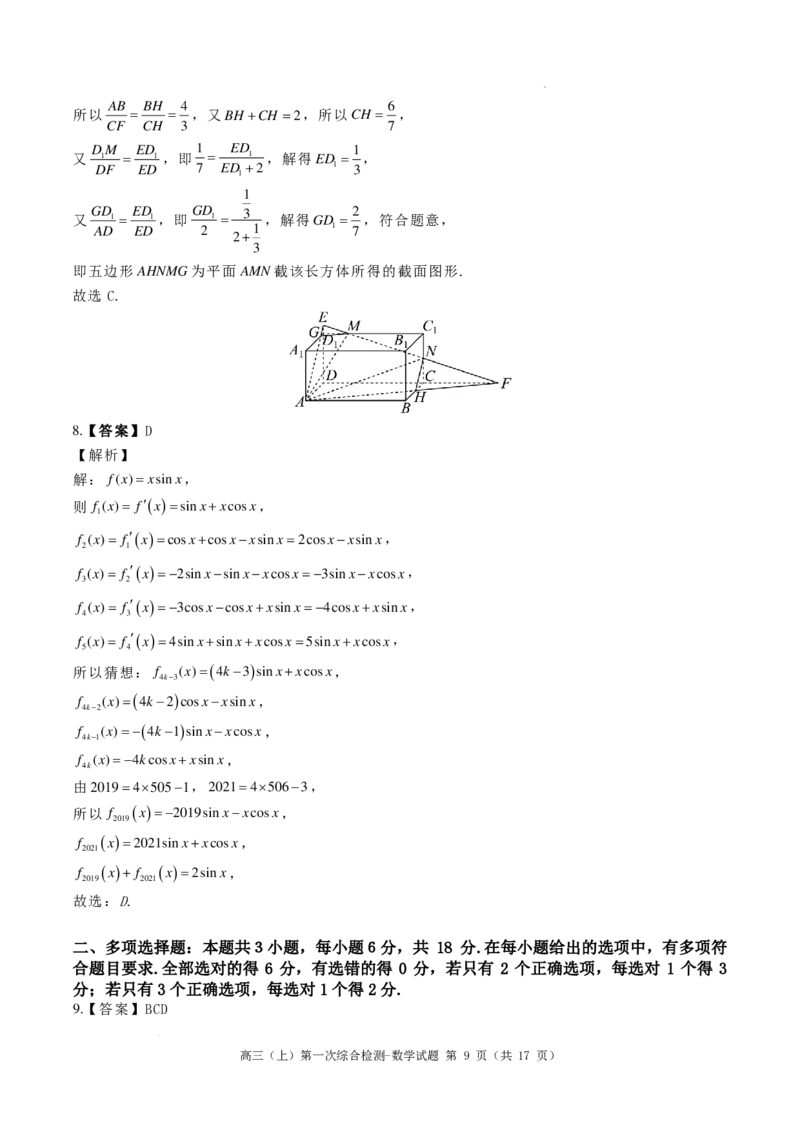17.（15分）如图，在四棱锥 中， 为正三角形，底面 为正方形，平面 平面 ，点 是棱 的中点，平面 与棱 交于点 . 𝑃𝑃 −𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 △𝑃𝑃𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 𝑃𝑃𝐴𝐴𝐴𝐴 ⊥ 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 𝑀𝑀 𝑃𝑃𝐴𝐴 𝐴𝐴𝐴𝐴𝑀𝑀 𝑃𝑃𝐴𝐴 𝑁𝑁 （1）求证： 平面 ； （ ） 为平面 内一动点， 为线段 上一点； 𝑀𝑀𝑁𝑁// 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 ①求证： ； 2 𝑄𝑄 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀 𝐸𝐸 𝐴𝐴𝐴𝐴 ②当 最小时，求 的值. 𝑁𝑁𝑄𝑄 ⊥𝐴𝐴𝑃𝑃 𝑀𝑀𝑀𝑀 𝐴𝐴𝑄𝑄+𝑄𝑄𝐸𝐸 𝑀𝑀𝑄𝑄 高三（上）第一次综合检测-数学试题 第 4 页（共 17 页） 学科网（北京）股份有限公司18.（17分）已知抛物线E:y= x2，过点T(1,2)的直线与抛物线E交于 A,B两点，设抛物线E在点 A,B处的切线分别为l 和l ，已知l 与 x轴交于点M,l 与 x轴交于点 N ，设l 与l 的交点为P. 1 2 1 2 1 2 (1)证明：点 P在定直线上； (2)若PMN面积为 2，求点P的坐标； (3)若 P,M,N,T四点共圆，求点P的坐标. 19.（17分）设函数 f (x)的导函数为 f′(x), f′(x)的导函数为 f′′(x), f′′(x)的导函数为 f′′′(x).若 f′′(x )=0，且 f′′′(x )≠0，则 ( x , f (x )) 为曲线 y= f (x)的拐点. 0 0 0 0 (1)判断曲线 y=x6是否有拐点，并说明理由；  2  2 (2)已知函数 f (x)=ax5−5x3，若 , f  为曲线 y= f (x)的一个拐点，求 f (x)的单调区间与     2  2  极值. 高三（上）第一次综合检测-数学试题 第 5 页（共 17 页） 学科网（北京）股份有限公司数学参考答案 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 1.【答案】D 【解析】根据不等式 xy≤ x2+y2 可得 4a2+b2 ⋅ a2+4b2 ≤ 4a2+b2+a2+4b2 = 5( a2+b2)， 2 2 2 当且仅当4a2+b2 =a2+4b2，即a2 =b2时等号成立， 4a2+b2 ⋅ a2+4b2 5 5 所以， ≤ ，所以m= . a2+b2 2 2 所以，不等式x2−ax+b<0的解集为(1,5). 根据一元二次不等式的解集与一元二次方程解的关系可知， 1和5是方程x2−ax+b=0的两个解， 1+5=a a=6 所以有 ，所以 ，a+b=11. 1×5=b b=5 故选：D. 2.【答案】A 【解析】因为 y=log x在(0,+∞)上单调递减，所以log 10.5−1 >1，所以 ( 0.3−1)0.4 > ( 0.5−1)0.4 >10.4，即0.3−0.4 >0.5−0.4 >1，故 3 b>c>1， 所以b>c>a. 故选：A. 3.【答案】D 【解析】因 AB= AC,AB⊥ AC,取 BC中点为 N，则 AN ⊥BC，又 AD⊥BC， AN,AD⊂平面 AND， ANAD= A， 则BC ⊥平面 AND，BC⊂面 ABC，则平面 ABC ⊥平面 AND，要使四面体 ABCD的体积最大，则有 DN ⊥平面 ABC，且球心 O在 DN上. 1 11  设球体半径为 R，则OA=OD=R，则V = S ⋅DN =  BC⋅AN⋅(R+ON)， D−ABC 3 ABC 32  又注意到BC =2AN， AN2 =OA2−ON2 =R2−ON2，则 1 1 1 V = S ⋅DN = AN2⋅(R+ON)= (R+ON)2(R−ON). D−ABC 3 ABC 3 3 1 1 1 2R+2ON+2R−2ON  3 1 4R 3 注意到 (R+ON)2(R−ON)= (R+ON)(R+ON)(2R−2ON)≤ ⋅  = ⋅  . 3 6 6  3  6  3  高三（上）第一次综合检测-数学试题 第 6 页（共 17 页） 学科网（北京）股份有限公司4 当且仅当2R−2ON =R+ON ，即R=3ON时取等号.又四面体 ABCD的体积的最大值为 ，则 3 3 1 4R 4 3 ⋅  = ⇒R= . 6  3  3 2 则球的表面积为4πR2 =9π. 故选：D 4.【答案】D x x x x 【解析】由 asin2x≥2sin 1−sinx，可得2asinxcosx≥2sin (sin −cos )2 ， 2 2 2 2  π x  π x x 因为 x∈ 0,  ，可得 ∈  0,  ，所以sin 2，而− 2 ≤ 2sin2x− ≤ 2，则 g(x)>0，即函数 g(x)在(−∞, ]上 4 2  4 4 无零点， 当 x≥π时，3−2x≤3−2π<−3，则g(x)<0，即函数 g(x)在[π,+∞)上无零点， π π π π 7π π 2 当 0,g(π)<0，因此函数g(x)在( ,π)上有唯一零点， 4 4 π 从而方程 2sin(2x − )=2x −3有唯一实根，过点(2,0)作曲线 y= f (x)的切线有且只有一条，D 正 0 4 0 确. 故选：BCD 10.【答案】AD π  π  π 【解析】因为 y=2sinxcosx=sin2x，向右平移 个单位得 f (x)=sin2x− =sin2x− ，则最小 6  6  3 2π 正周期为T = =π，故 A 选项正确； 2 高三（上）第一次综合检测-数学试题 第 10 页（共 17 页） 学科网（北京）股份有限公司π π π π 5π 令− +2kπ≤2x− ≤ +2kπ，解得− +kπ≤x≤ +kπ，所以单调递增区间为 2 3 2 12 12  π 5π  − +kπ, +kπ ,k∈Z，故 B 选项错误；    12 12  π π 5π kπ 令2x− = +kπ,解得 x= + ,k∈Z，故 C 选项错误； 3 2 12 2 π π π  令2x− =kπ,解得 x= +kπ,k∈Z所以函数 f (x)的对称中心为 +kπ,0,k∈Z，故 D 选项正确. 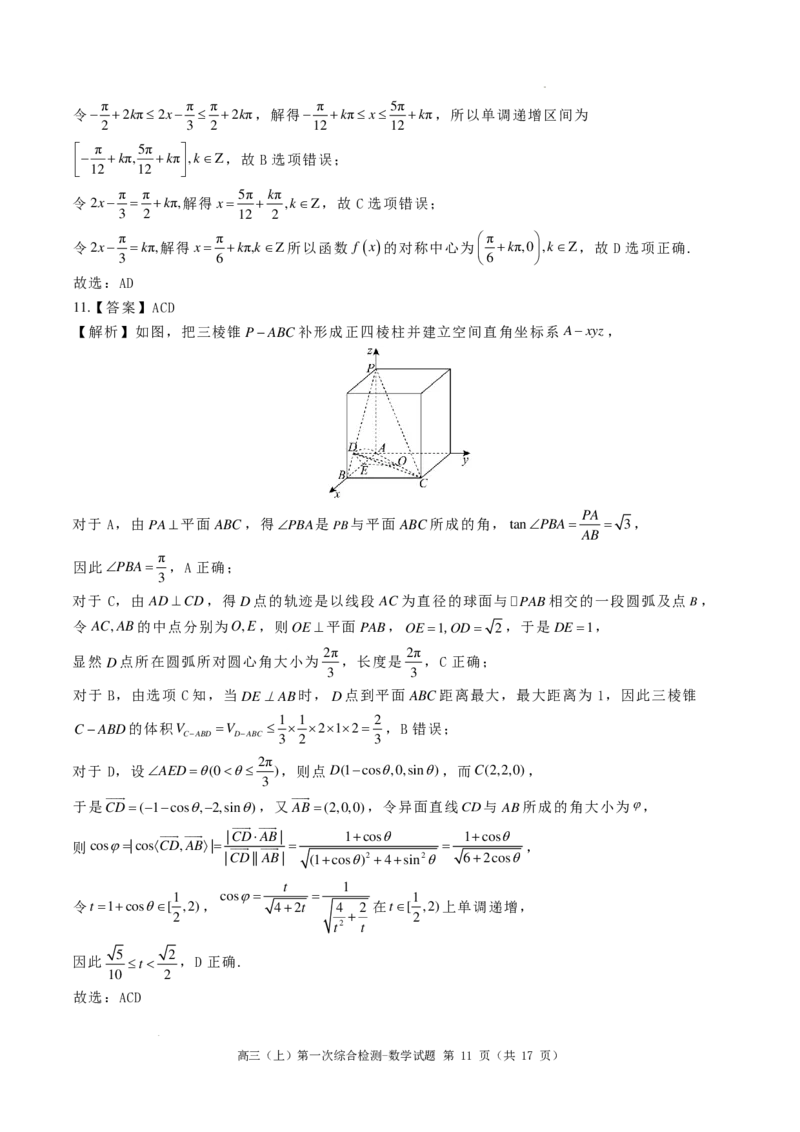3 6 6  故选：AD 11.【答案】ACD 【解析】如图，把三棱锥 P−ABC补形成正四棱柱并建立空间直角坐标系 A−xyz， PA 对于 A，由PA⊥平面 ABC，得∠PBA是PB与平面 ABC所成的角，tan∠PBA= = 3， AB π 因此∠PBA= ，A 正确； 3 对于 C，由 AD⊥CD，得D点的轨迹是以线段 AC为直径的球面与PAB相交的一段圆弧及点B， 令 AC,AB的中点分别为O,E，则OE⊥平面PAB，OE=1,OD= 2，于是DE=1， 2π 2π 显然D点所在圆弧所对圆心角大小为 ，长度是 ，C 正确； 3 3 对于 B，由选项 C 知，当DE⊥AB时，D点到平面 ABC距离最大，最大距离为 1，因此三棱锥 1 1 2 C−ABD的体积V =V ≤ × ×2×1×2= ，B 错误； C−ABD D−ABC 3 2 3 2π 对于 D，设∠AED=θ(0<θ≤ )，则点D(1−cosθ,0,sinθ)，而C(2,2,0)， 3   于是CD=(−1−cosθ,−2,sinθ)，又 AB=(2,0,0)，令异面直线CD与 AB所成的角大小为ϕ，     |CD⋅AB| 1+cosθ 1+cosθ 则cosϕ=|cos〈CD,AB〉|=   = = ， |CD||AB| (1+cosθ)2+4+sin2θ 6+2cosθ t 1 1 cosϕ= = 1 令t=1+cosθ∈[ ,2)， 4+2t 4 2 在t∈[ ,2)上单调递增， 2 + 2 t2 t 5 2 因此 ≤t< ，D 正确. 10 2 故选：ACD 高三（上）第一次综合检测-数学试题 第 11 页（共 17 页） 学科网（北京）股份有限公司三、填空题：本大题共 3个小题，每小题5分，共 15 分. 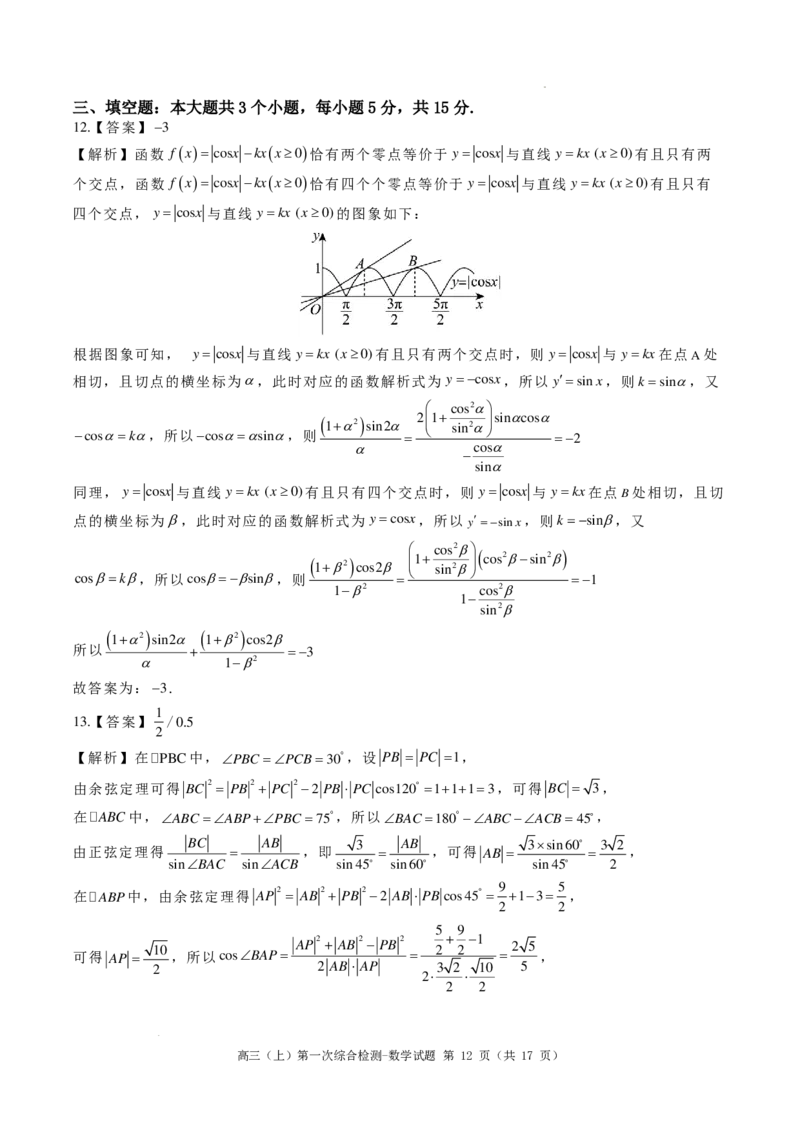12.【答案】−3 【解析】函数 f (x)= cosx −kx(x≥0)恰有两个零点等价于 y= cosx 与直线 y=kx (x≥0)有且只有两 个交点，函数 f (x)= cosx −kx(x≥0)恰有四个个零点等价于 y= cosx 与直线 y=kx (x≥0)有且只有 四个交点， y= cosx 与直线 y=kx (x≥0)的图象如下： 根据图象可知， y= cosx 与直线 y=kx (x≥0)有且只有两个交点时，则 y= cosx 与 y=kx在点A处 相切，且切点的横坐标为α，此时对应的函数解析式为 y=−cosx，所以 y′=sinx，则k =sinα，又  cos2α −cosα=kα，所以−cosα=αsinα，则 ( 1+α2) sin2α = 2  1+ sin2α   sinαcosα =−2 α cosα − sinα 同理， y= cosx 与直线 y=kx (x≥0)有且只有四个交点时，则 y= cosx 与 y=kx在点B处相切，且切 点的横坐标为β，此时对应的函数解析式为 y=cosx，所以 y′=−sinx，则k =−sinβ，又 ( 1+β2) cos2β    1+ c s o in s 2 2 β β   ( cos2β−sin2β ) cosβ=kβ，所以cosβ=−βsinβ，则 = =−1 1−β2 cos2β 1− sin2β ( 1+α2) sin2α ( 1+β2) cos2β 所以 + =−3 α 1−β2 故答案为：−3. 1 13.【答案】 /0.5 2 【解析】在PBC中，∠PBC =∠PCB=30°，设 PB = PC =1， 由余弦定理可得 BC 2 = PB 2+ PC 2−2 PB ⋅ PC cos120° =1+1+1=3，可得 BC = 3， 在ABC中，∠ABC =∠ABP+∠PBC =75°，所以∠BAC =180°−∠ABC−∠ACB=45， BC AB 3 AB 3×sin60 3 2 由正弦定理得 = ，即 = ，可得 AB = = ， sin∠BAC sin∠ACB sin45 sin60 sin45 2 9 5 在ABP中，由余弦定理得 AP 2 = AB 2+ PB 2−2 AB ⋅ PB cos45° = +1−3= ， 2 2 5 9 10 AP 2+ AB 2− PB 2 2 + 2 −1 2 5 可得 AP = ，所以cos∠BAP= = = ， 2 2 AB ⋅ AP 3 2 10 5 2⋅ ⋅ 2 2 高三（上）第一次综合检测-数学试题 第 12 页（共 17 页） 学科网（北京）股份有限公司5 sin∠BAP 1 可得sin∠BAP= 1−cos2∠BAP = ，因此tan∠BAP= = . 5 cos∠BAP 2 1 故答案为： 2 14.【答案】3n−2n 【解析】因为每行的第 n个数从上到下形成以2n−1为首项，以 3 为公比的等比数列， 所以S =30×2n−1+31×2n−2+32×2n−3++3n−1×20, n  n−1 n−2 n−3 0 2 2 2 2 所以S =3n−1×  +  +  ++   n  3 3 3 3   n 2 1−    n S =3n−1× 3 =3n×1− 2   =3n−2n. n  1− 2   3    3   故答案为：3n−2n. 四、解答题：本大题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤. 15.（13分）【答案】(1)更可能是专业评委打的分数 (2)事件 M 与事件 N 不独立. 【解析】（1）可以用方差来度量每一组评委打分的相似性，方差越小，相似程度越高. 42+45+48+53+52+47+49 x = =48， A 7 48+52+70+66+77+49+51 x = =59， B 7 所以A组数据的方差是 1 88 s2 = (42−48)2+(45−48)2+(48−48)2+(53−48)2+(52−48)2+(47−48)2+(49−48)2 = ， A 7   7 B组数据的方差是 1 828 s2 = (48−59)2+(52−59)2+(70−59)2+(66−59)2+(77−59)2+(49−59)2+(51−59)2 = ， B 7   7 因为专业评委给分更符合专业规则，所以相似程度更高，因此组分数更可能是专业评委打的分 数. C1 2 （2）P(M)= 6 = ， C2 7 7 N:a+b=100:48+52=100,47+53=100， c+d =100:48+52=100,49+51=100，各有两种， 高三（上）第一次综合检测-数学试题 第 13 页（共 17 页） 学科网（北京）股份有限公司2 2 C1C1 4×C2−C1C1 80 所以P(N)= + − 2 2 = 7 2 2 = ， C2 C2 C2?C2 C2C2 441 7 7 7 7 7 7 事件MN：当a+b=48+52=100时， c,d可以任意，有C2种， 7 当a，b中有一个数据为 48，另一个不是 52 时，则c+d =100，有C1C1种， 5 2 C2 C1C1 31 所以P(MN)= 7 + 5 2 = ， C2C2 C2C2 441 7 7 7 7 ∴P(M)P(N)≠P(MN)，则事件M 与事件 N 不独立. π 16.（15分）【答案】(1)∠DBC = ， AB=2 3 ；(2)( 3,2] 6 π DC 2 1 π 【解析】（1）由题易知∠ABC< ,由正弦定理得sin∠DBC = = = ，∴∠DBC = ， 2 2R 4 2 6 π π π ∴∠DAB+∠DBA=∠DAB+∠ABC−∠DBC = − = ， 2 6 3 2π ∴∠ADB=π−(∠DAB+∠DBA)= ， 3 3 ∴AB=2R×sin∠ADB=4× =2 3. 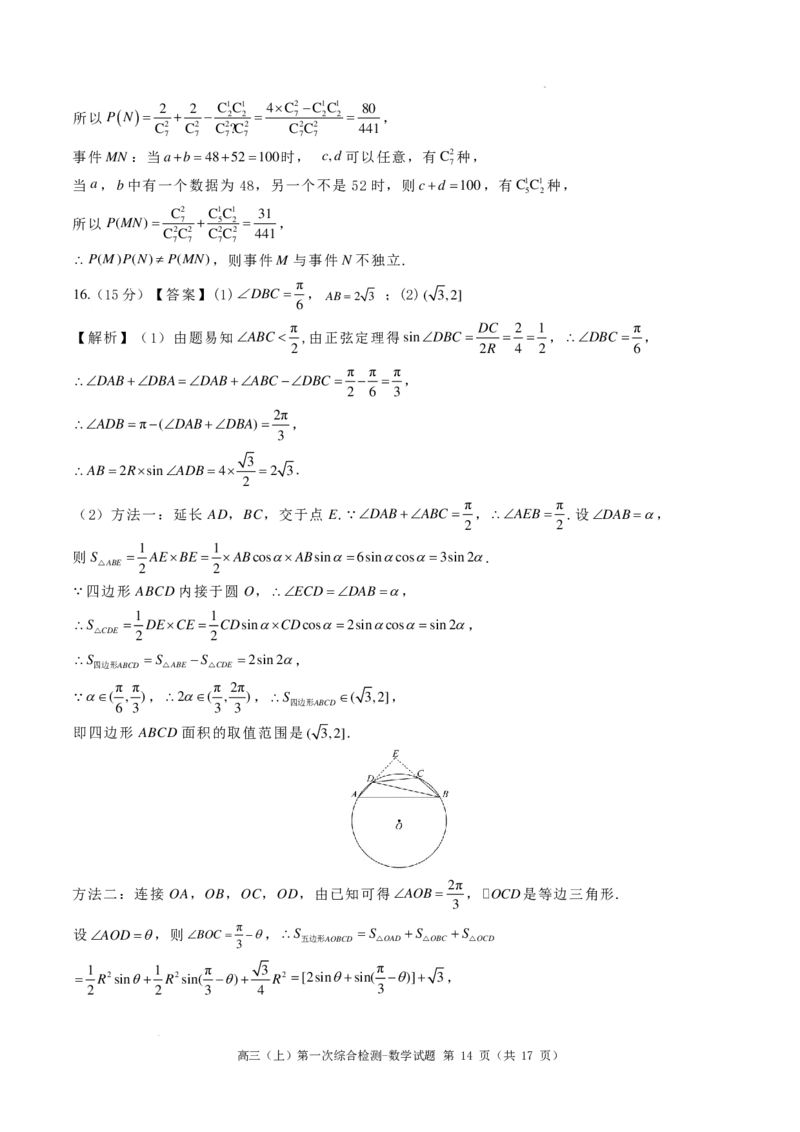2 π π （2）方法一：延长 AD，BC，交于点 E.∠DAB+∠ABC = ，∴∠AEB= .设∠DAB=α， 2 2 1 1 则S = AE×BE= ×ABcosα×ABsinα=6sinαcosα=3sin2α. △ABE 2 2 四边形 ABCD内接于圆 O，∴∠ECD=∠DAB=α， 1 1 ∴S = DE×CE= CDsinα×CDcosα=2sinαcosα=sin2α， △CDE 2 2 ∴S =S −S =2sin2α， 四边形ABCD △ABE △CDE π π π 2π α∈( , )，∴2α∈( , )，∴S ∈( 3,2]， 6 3 3 3 四边形ABCD 即四边形 ABCD面积的取值范围是( 3,2]. 2π 方法二：连接 OA，OB，OC，OD，由已知可得∠AOB= ，OCD是等边三角形. 3 π 设∠AOD=θ，则∠BOC= −θ，∴S =S +S +S 3 五边形AOBCD △OAD △OBC △OCD 1 1 π 3 π = R2sinθ+ R2sin( −θ)+ R2 =[2sinθ+sin( −θ)]+ 3， 2 2 3 4 3 高三（上）第一次综合检测-数学试题 第 14 页（共 17 页） 学科网（北京）股份有限公司1 2π 又S = R2sin = 3， △AOB 2 3 π π ∴S =S −S =2[sinθ+sin( −θ)]=2sin(θ+ )， 四边形ABCD 五边形AOBCD △AOB 3 3 π π π 2π θ∈(0, )，∴θ+ ∈( , )， 3 3 3 3 ∴S ∈( 3,2]，即四边形 ABCD面积的取值范围是( 3,2]. 四边形ABCD 17.（15分）【答案】（1）证明见解析； （2）①证明见解析；② . 1 【解析】（1）证明：因为 平面 平面 2 所以 平面 ， 𝐴𝐴𝐴𝐴 // 𝐴𝐴𝐴𝐴,𝐴𝐴𝐴𝐴 ⊂ 𝐴𝐴𝐴𝐴𝑃𝑃,𝐴𝐴𝐴𝐴 ⊄ 𝐴𝐴𝐴𝐴𝑃𝑃, 又 平面 ，平面 平面 𝐴𝐴𝐴𝐴 // 𝐴𝐴𝐴𝐴𝑃𝑃 所以 . 𝐴𝐴𝐴𝐴 ⊂ 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀∩ 𝐴𝐴𝐴𝐴𝑃𝑃 =𝑀𝑀𝑁𝑁, 又 平面 平面 ， 𝐴𝐴𝐴𝐴 // 𝑀𝑀𝑁𝑁 所以 平面 . 𝐴𝐴𝐴𝐴 ⊂ 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴,𝑀𝑀𝑁𝑁 ⊄ 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 (2)解：①由平面 平面 又平面 平面 ， 𝑀𝑀𝑁𝑁 // 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 所以 平面 ，所以 ，由（ ）， ，故 ， 𝑃𝑃𝐴𝐴𝐴𝐴 ⊥ 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴,𝐴𝐴𝐴𝐴 ⊥𝐴𝐴𝐴𝐴, 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴∩ 𝑃𝑃𝐴𝐴𝐴𝐴 =𝐴𝐴𝐴𝐴 又 是棱 的中点，则 为棱 中点， 为正三角形， 𝐴𝐴𝐴𝐴 ⊥ 𝑃𝑃𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴 ⊥𝐴𝐴𝑃𝑃 1 𝐴𝐴𝐴𝐴 // 𝑀𝑀𝑁𝑁 𝐴𝐴𝑃𝑃 ⊥𝑀𝑀𝑁𝑁 所以 平面 ， 𝑀𝑀 𝑃𝑃𝐴𝐴 𝑁𝑁 𝑃𝑃𝐴𝐴 △𝑃𝑃𝐴𝐴𝐴𝐴 所以 平面 ，且 平面 ， 𝐴𝐴𝑃𝑃 ⊥𝑁𝑁𝐴𝐴,𝑀𝑀𝑁𝑁∩𝑁𝑁𝐴𝐴 =𝑁𝑁,𝑀𝑀𝑁𝑁,𝑁𝑁𝐴𝐴 ⊂ 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀 所以 . 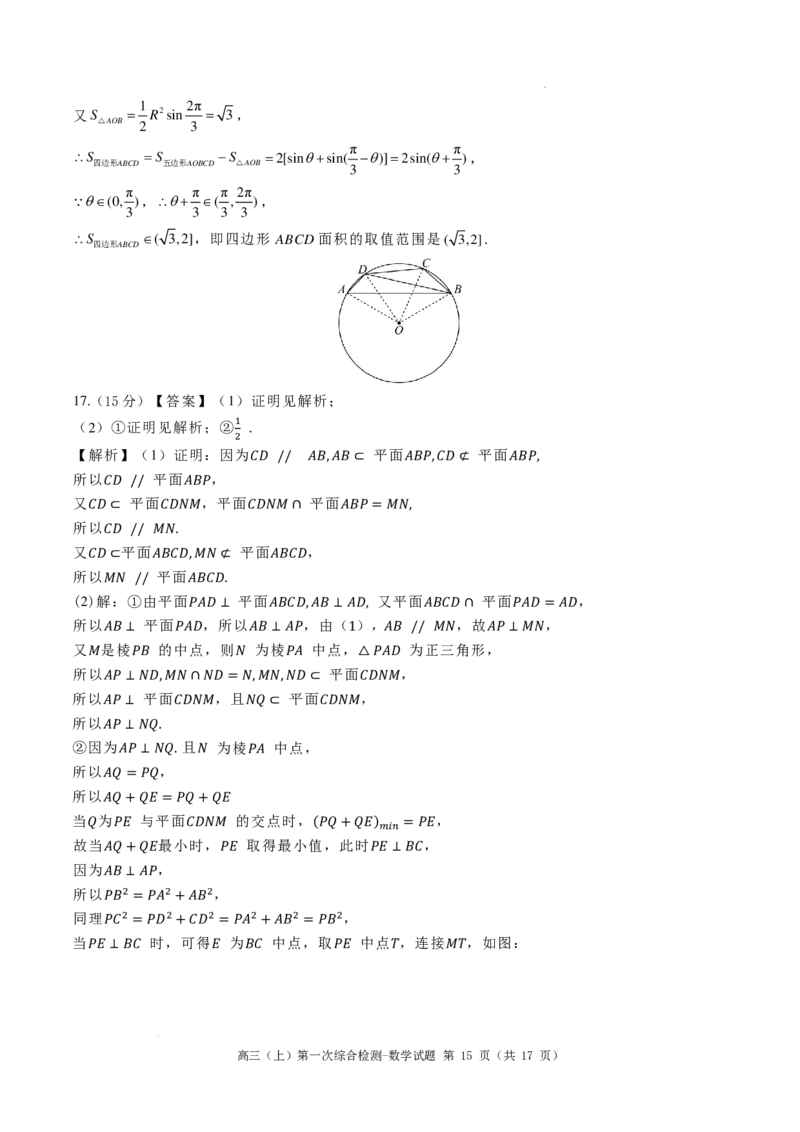𝐴𝐴𝑃𝑃 ⊥ 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀 𝑁𝑁𝑄𝑄 ⊂ 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀 ②因为 .且 为棱 中点， 𝐴𝐴𝑃𝑃 ⊥𝑁𝑁𝑄𝑄 所以 ， 𝐴𝐴𝑃𝑃 ⊥𝑁𝑁𝑄𝑄 𝑁𝑁 𝑃𝑃𝐴𝐴 所以 𝐴𝐴𝑄𝑄 =𝑃𝑃𝑄𝑄 当 为 与平面 的交点时， ， 𝐴𝐴𝑄𝑄 +𝑄𝑄𝐸𝐸 =𝑃𝑃𝑄𝑄+𝑄𝑄𝐸𝐸 故当 最小时， 取得最小值，此时 ， 𝑄𝑄 𝑃𝑃𝐸𝐸 𝐴𝐴𝐴𝐴𝑁𝑁𝑀𝑀 (𝑃𝑃𝑄𝑄+𝑄𝑄𝐸𝐸)𝑚𝑚𝑚𝑚𝑚𝑚 =𝑃𝑃𝐸𝐸 因为 ， 𝐴𝐴𝑄𝑄 +𝑄𝑄𝐸𝐸 𝑃𝑃𝐸𝐸 𝑃𝑃𝐸𝐸 ⊥𝐴𝐴𝐴𝐴 所以 ， 𝐴𝐴𝐴𝐴 ⊥𝐴𝐴𝑃𝑃 同理 2 2 2 ， 𝑃𝑃𝐴𝐴 =𝑃𝑃𝐴𝐴 +𝐴𝐴𝐴𝐴 当 2 时，2 可得2 为 2 中点2，取 2 中点 ，连接 ，如图： 𝑃𝑃𝐴𝐴 =𝑃𝑃𝐴𝐴 +𝐴𝐴𝐴𝐴 =𝑃𝑃𝐴𝐴 +𝐴𝐴𝐴𝐴 =𝑃𝑃𝐴𝐴 𝑃𝑃𝐸𝐸 ⊥𝐴𝐴𝐴𝐴 𝐸𝐸 𝐴𝐴𝐴𝐴 𝑃𝑃𝐸𝐸 𝑇𝑇 𝑀𝑀𝑇𝑇 高三（上）第一次综合检测-数学试题 第 15 页（共 17 页） 学科网（北京）股份有限公司则有 且 ， 1 1 有 ， 𝑀𝑀𝑇𝑇 // 𝐴𝐴𝐸𝐸 𝑀𝑀𝑇𝑇 =2𝐴𝐴𝐸𝐸 =2𝐸𝐸𝐴𝐴 所以 . 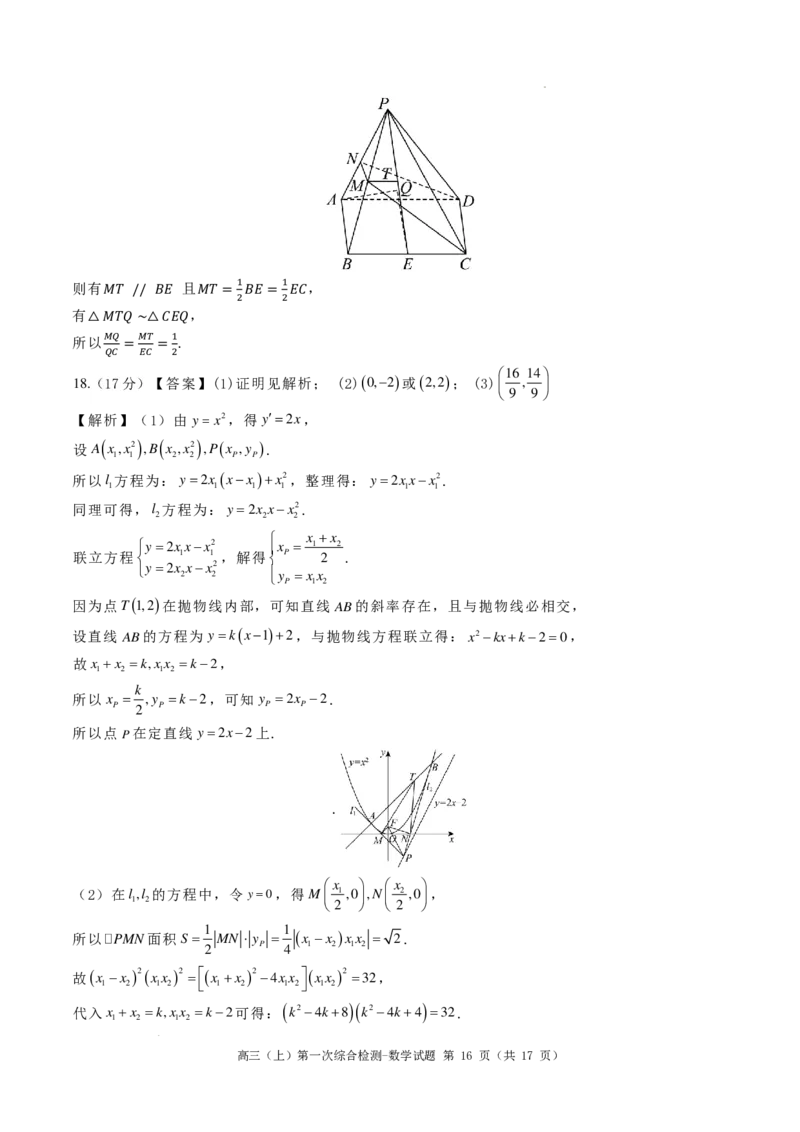△𝑀𝑀𝑇𝑇𝑄𝑄 ∼△𝐴𝐴𝐸𝐸𝑄𝑄 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀 1 18.（1 𝑀𝑀 7 𝑄𝑄 分 = ） 𝐸𝐸𝑄𝑄 【 = 答 2 案】(1)证明见解析； (2)(0,−2)或(2,2)； (3)   16 , 14   9 9  【解析】（1）由 y  x2，得 y′=2x， 设 A ( x,x2) ,B ( x ,x2) ,P(x ,y ). 1 1 2 2 P P 所以l 方程为： y=2x (x−x )+x2，整理得： y=2xx−x2. 1 1 1 1 1 1 同理可得，l 方程为： y=2x x−x2. 2 2 2  x +x y=2xx−x2 x = 1 2 联立方程 1 1 ，解得 P 2 . y=2x 2 x−x 2 2  y =xx P 1 2 因为点T(1,2)在抛物线内部，可知直线 AB的斜率存在，且与抛物线必相交， 设直线 AB的方程为 y=k(x−1)+2，与抛物线方程联立得：x2−kx+k−2=0， 故 x +x =k,xx =k−2， 1 2 1 2 k 所以 x = ,y =k−2，可知 y =2x −2. P 2 P P P 所以点P在定直线 y=2x−2上. . x  x  （2）在l,l 的方程中，令 y=0，得M 1,0,N 2 ,0， 1 2  2   2  1 1 所以PMN面积S = MN ⋅ y = (x −x )xx = 2. 2 P 4 1 2 1 2 故(x −x )2(xx )2 =(x +x )2−4xx (xx )2 =32， 1 2 1 2  1 2 1 2 1 2 代入 x +x =k,xx =k−2可得： ( k2−4k+8 )( k2−4k+4 ) =32. 1 2 1 2 高三（上）第一次综合检测-数学试题 第 16 页（共 17 页） 学科网（北京）股份有限公司整理得  (k−2)2+8    (k−2)2−4  =0，解得：k =0或k =4. 所以点P的坐标为(0,−2)或(2,2).  1 x  1 1 （3）抛物线焦点F  0, 4   ，由M  2 1,0  得直线MF斜率k MF =− 2x =− k ， 1 MP 可知MF ⊥MP， 同理 NF ⊥NP，所以PF是PMN外接圆的直径. 若点T也在该圆上，则TF ⊥TP. 7 4 由k = ，得直线TP的方程为： y=− (x−1)+2. TF 4 7 又点P在定直线 y=2x−2上，  16  4 x= y=− (x−1)+2   9 联立两直线方程 7 ，解得 ，  y=2x−2  y= 14  9 16 14 所以点P的坐标为 , .  9 9  19.（17分）【答案】(1)没有拐点，理由见解析. (2)单调递增区间为(−∞,−1),(1,+∞)；单调递减区间为[−1,1]，极大值为 2，极小值为−2. 【解析】（1）解：由函数 y=x6，可得 y′=6x5,y′′=30x4,y′′′=120x3， 由30x4 =0，得 x=0，又由120x3 =0，得 x=0，所以曲线 y=x6没有拐点. （2）解：由函数 f (x)=ax5−5x3， 可得 f′(x)=5ax4−15x2, f′′(x)=20ax3−30x=10x ( 2ax2−3 ) ，  2  2  2 因为 , f  为曲线 y= f (x)的一个拐点，所以 f′′ =0，       2  2   2  1  2 所以2a× −3=0，解得a=3，经检验，当a=3时， f′′′    ≠0， 2  2  所以 f′(x)=15x4−15x2 =15x2( x2−1 ) . 当 x<−1或 x>1时， fx0，则 f (x)的单调递增区间为(−∞,−1),(1,+∞)； 当−1≤x≤1时， f′(x)≤0，且 f′(x)=0不恒成立，则 f (x)的单调递减区间为[−1,1]， 故当 x=−1时， f (x)取得极大值，且极大值为2； 当 x=1时， f (x)取得极小值，且极小值为−2. 高三（上）第一次综合检测-数学试题 第 17 页（共 17 页） 学科网（北京）股份有限公司