文档内容
5.3.1 函数的单调性与导数
重点练
一、单选题
1.若 在 内单调递减,则实数 的取值范围是( )
A. B. C. D.
2.若函数 在区间 单调递增,则 的取值范围是( )
A. B. C. D.
3.已知函数 ,则 是 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.若定义在 上的函数 满足 , ,则不等式 (其中 为
自然对数的底数)的解集为( )
A. B.
C. D.
二、填空题
5.已知函数 ,则使得 成立的 范围是_______.
6.已知函数 在 上有增区间,则a的取值范围是_______.
三、解答题7.已知函数 .
(1)当 时,求函数 的单调区间;
(2)若函数 有两个零点,求实数 的取值范围.参考答案
1.【答案】A
【解析】 ,由 在 单调递减,
∴ ,∴ ,∴ .
故选A
2.【答案】C
【解析】由 知, ,
因为 在 上单调递增,
所以 在 上恒成立,
即 ,则 在 上恒成立,
令 ,
因为 在 上恒成立,
所以 在 上单调递减,则 ,
所以 .
故选C.
3.【答案】C
【解析】由题意可得: 恒成立,所以函数 在 上递增,
又 ,所以函数 是奇函数,当 时,即 ,所以 ,即 ;
当 时,即 ,所以 ,即 ,
所以“ ”是“ ”的充要条件.
故选C.
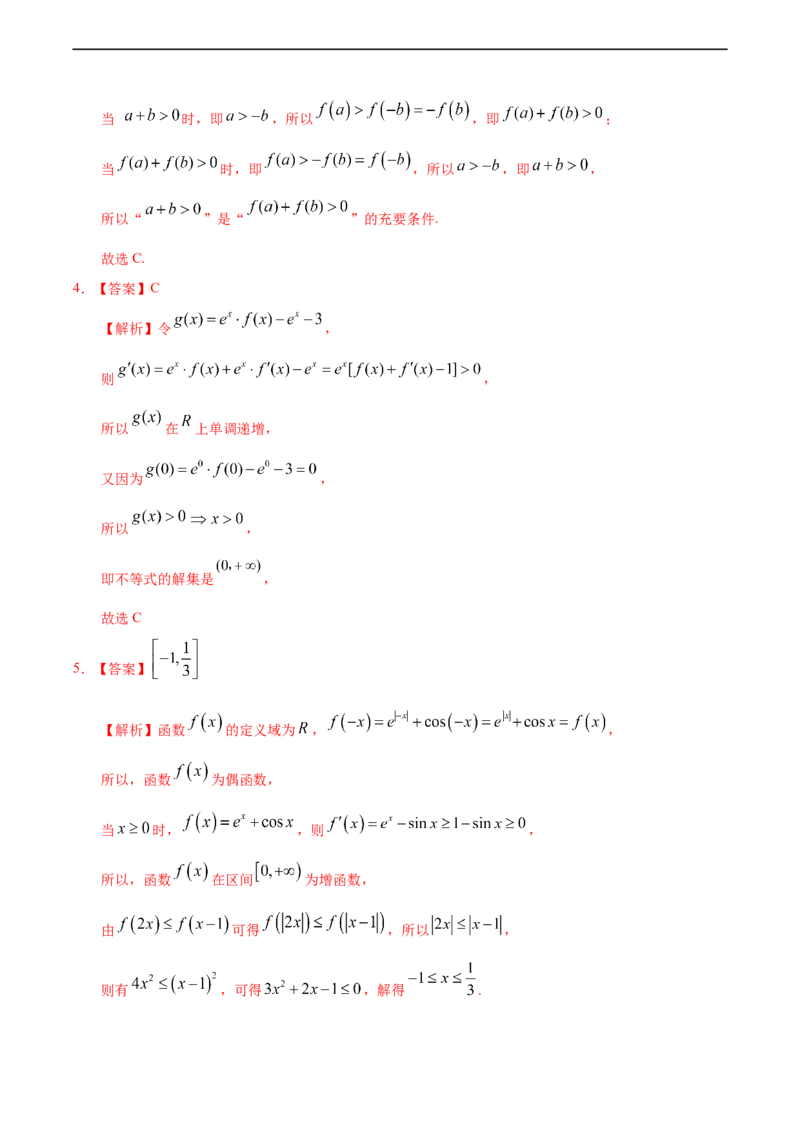
4.【答案】C
【解析】令 ,
则 ,
所以 在 上单调递增,
又因为 ,
所以 ,
即不等式的解集是 ,
故选C
5.【答案】
【解析】函数 的定义域为 , ,
所以,函数 为偶函数,
当 时, ,则 ,
所以,函数 在区间 为增函数,
由 可得 ,所以 ,
则有 ,可得 ,解得 .因此,使得 成立的 范围是 .
故填 .
6.【答案】
【解析】由题得 ,
因为函数 在 上有增区间,
所以存在 使得 成立,
即 成立,
因为 时, ,
所以 .
故填
7.【答案】(1)单调递减区间是 ,单调递增区间是 ;(2) .
【解析】(1) 的定义域是 ,
当 时, ,
,当 时, , ,所以 ;
当 时, , ,所以 ,
所以 的单调递减区间是 ,单调递增区间是 .
(2)函数 有两个零点等价于方程 有两个不等的实数根,
又函数 的定义域为 ,
所以 有两个不等的实数跟,
设 ,
则 ,
,
设 ,
易知 在 上单调递减,且 ,
当 时, , , 单调递增,
当 时, , , 单调递减,
所以 ,
又 时, ,时, ,
所以实数 的取值范围是 .