文档内容
2024-2025 学年浙江省强基联盟高一下学期 3 月月考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合 ,集合 ,则 的元素个数是( )
A={−5,−3,−1,0,2,4,8} B={x∣x2<16} A∩B
A. 4个 B. 5个 C. 6个 D. 7个
2.cos570∘=( )
√3 1 √3 1
A. B. − C. − D.
2 2 2 2
⃗ ⃗
⃗ ⃗ 2⃗
3.已知向量 a=(m,−1) , b=(−2,1) ,若a⊥(a+ b),则实数m=( )
3
1 1 1 1
A. −1或− B. 1或− C. −1或 D. 1或
3 3 3 3
1
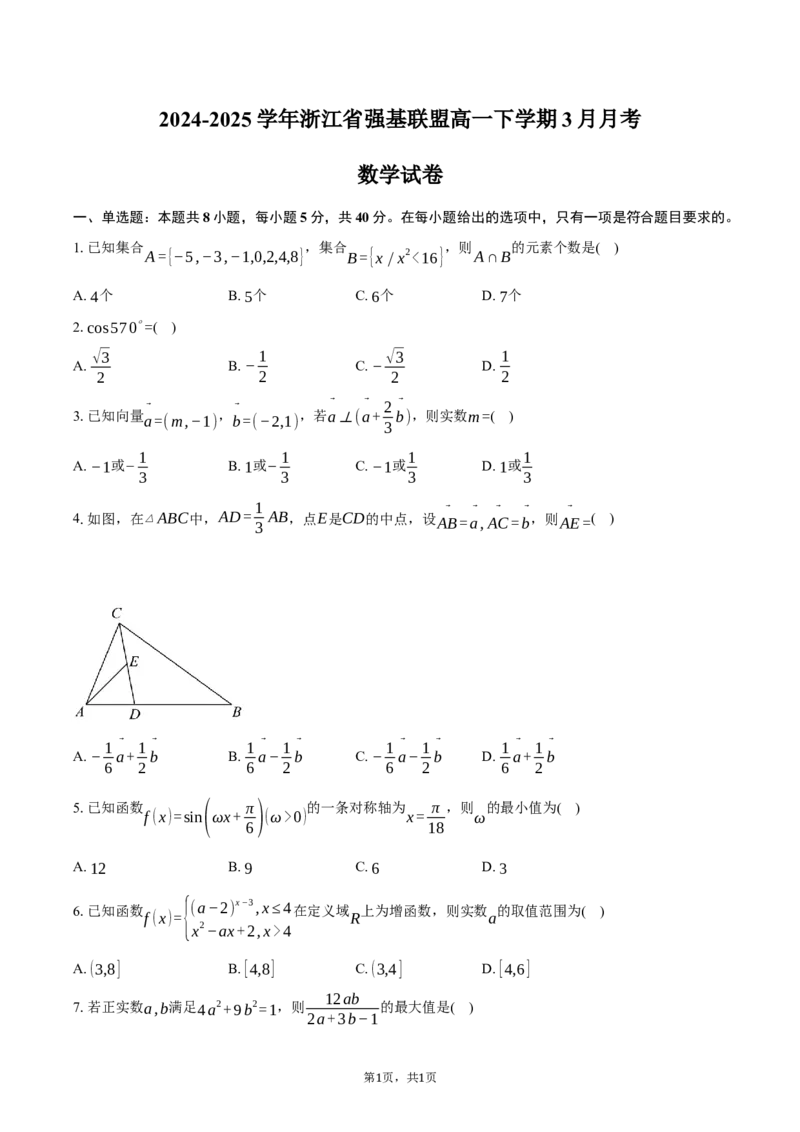
4.如图,在▵ABC中,AD= AB,点E是CD的中点,设 A ⃗ B= ⃗ a,A ⃗ C= ⃗ b ,则 A ⃗ E=( )
3
1⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗
A. − a+ b B. a− b C. − a− b D. a+ b
6 2 6 2 6 2 6 2
5.已知函数 ( π) 的一条对称轴为 π ,则 的最小值为( )
f (x)=sin ωx+ (ω>0) x= ω
6 18
A. 12 B. 9 C. 6 D. 3
6.已知函数 {(a−2) x−3,x≤4在定义域 上为增函数,则实数 的取值范围为( )
f (x)= R a
x2−ax+2,x>4
A. (3,8] B. [4,8] C. (3,4] D. [4,6]
12ab
7.若正实数a,b满足4a2+9b2=1,则 的最大值是( )
2a+3b−1
第 页,共 页
1 1A. 1−√2 B. 1+√2 C. √2−1 D. √2
8.已知函数f(x),g(x)的定义域均为R,且f(x)+g(x)=6,f(5−x)−g(x−3)=2,若g(x)为奇函数,
n
则使 成立的 的最小值是( )
∑f(i)<0 n
i=1
A. 5 B. 6 C. 7 D. 8
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
1 √3
9.已知复数z= − i,则下列说法正确的是( )
2 2
√3
A. z的虚部为− i B. |z|2=|z2|
2
C. z3=−1 D. z是方程x2+x+1=0的根
10.已知函数 ,则( )
f (x)=ax−log (4x+1)(a∈R)
2
A. 当a=1时,函数f (x)为奇函数
B. 当a=1时,函数f (x)为偶函数
C. 当a=2时,函数f (x)的值域为(−∞,0)
D. 当 时,函数 的图象关于点( 1)成中心对称
a=2 g(x)=2f(x) 0,
2
⃗ ⃗
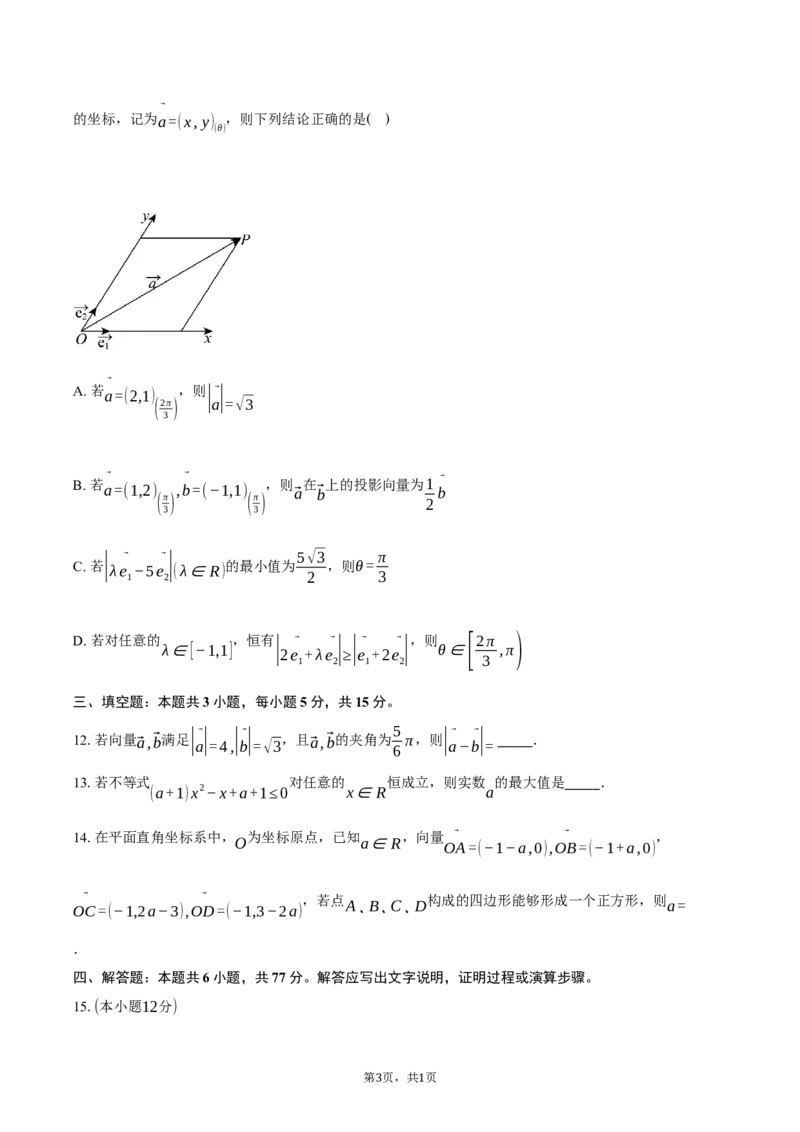
11.如图,设x轴和y轴是平面内相交成θ角的两条数轴,其中θ∈(0,π),e
,e
分别是与x轴,y轴正方向
1 2
⃗ ⃗ ⃗ ⃗
同向的单位向量,若向量OP=a=xe + ye ,则把有序数对(x,y)叫做向量⃗OP在夹角为θ的坐标系xOy中
1 2
第 页,共 页
2 1⃗
的坐标,记为a=(x,y) ,则下列结论正确的是( )
(θ)
⃗
A. 若 a=(2,1) ,则|⃗|
(2π) a =√3
3
B. 若 ⃗ a=(1,2) , ⃗ b=(−1,1) ,则 ⃗a 在 ⃗b 上的投影向量为1⃗ b
(π) (π)
2
3 3
C. 若 | λe ⃗ −5e ⃗| (λ∈R) 的最小值为 5√3 ,则θ= π
1 2 2 3
D. 若对任意的 ,恒有 | ⃗ ⃗| |⃗ ⃗| ,则 [2π )
λ∈[−1,1] 2e +λe ≥ e +2e θ∈ ,π
1 2 1 2 3
三、填空题:本题共3小题,每小题5分,共15分。
5
12.若向量⃗a,⃗b满足|⃗
a
|
=4,
|⃗
b
|
=√3
,且⃗a,⃗b的夹角为 π,则|⃗
a−
⃗
b
|
=
.
6
13.若不等式 对任意的 恒成立,则实数 的最大值是 .
(a+1)x2−x+a+1≤0 x∈R a
14.在平面直角坐标系中, 为坐标原点,已知 ,向量 ⃗ ⃗ ,
O a∈R OA=(−1−a,0),OB=(−1+a,0)
O ⃗ C=(−1,2a−3),O ⃗ D=(−1,3−2a) ,若点 A、B、C、D 构成的四边形能够形成一个正方形,则 a=
.
四、解答题:本题共6小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
第 页,共 页
3 1已知函数 .
f (x)=2cosx(√3cosx+sinx)−√3
(1)求函数f (x)的最小正周期;
若锐角 满足 (α π) 8 12,求 .
(2) α,β f − = ,cos(α+β)=− sinβ
2 6 5 13
16.(本小题12分)
已知复数z=3+mi(i是虚数单位,m∈R),且z⋅(3+i)为实数.
m+2i
(1)设复数z = ,求|z |;
1 1−2i 1
n−i2025
(2)设复数z = ,且复数z 在复平面内所对应的点在第二象限,求实数n的取值范围.
2 z 2
17.(本小题12分)
如图所示,某建筑物模型无下底面,有上底面,其外观是圆柱,底部挖去一个圆锥.已知圆柱与圆锥的底面
大小相同,圆柱的底面半径为6cm,高为20cm,圆锥母线为10cm.
计算该模型的体积 结果精确到
(1) .( 1cm3 )
(2)现需使用油漆对500个该种模型进行涂层,油漆费用为每平方米30元,总费用是多少?(结果精确到1
元)
18.(本小题12分)
已知四边形 ABCD 中, AD//BC,BC=2AD,E 为 CD 中点, F 为 BD 与 AE 的交点, ⃗ ⃗ ⃗ .
AE=x AD+ y AB
(1)求x+ y的值;
(2)若AB=2,BC=2√2,∠ABC=45∘,求cos∠AFB.
19.(本小题14分)
在▵ABC中,角A,B,C的对边分别为a,b,c,已知2c−b=2acosB.
(1)求角A;
第 页,共 页
4 1√19
(2)若b2−a2+c2−3c=0,且边BC的中线AD的长为 ,求▵ABC的面积;
2
a+b
(3)若▵ABC是锐角三角形,求 的范围.
c
20.(本小题15分)
定义:如果函数y=f (x)在区间[a,b]上有定义,且在区间(a,b)内存在一点c,使得
f (b)−f (a)=f (c)(b−a),则称c为函数y=f (x)的“偏移中值点”.已知函数
1
f (x)=2mx2− x+1(m∈R,x∈[−1,1]).
2
(1)当m=0时,判断函数y=f (x)是否有“偏移中值点”?如果有,求出“偏移中值点”,如果没有,请
说明理由;
1
(2)若 是函数y=f (x)的“偏移中值点”,求f (−1)+f (1)的值;
2
若函数 存在“偏移中值点”,求 ( 1) (1)的取值范围.
(3) y=f (x) f − +f
2 2
第 页,共 页
5 1参考答案
1.A
2.C
3.D
4.D
5.C
6.C
7.B
8.B
9.BC
10.BCD
11.ABD
12.√31
3
13.− 或−1.5
2
14.1或3
15.解: (1)f (x)=2√3cos2x+2sinxcosx−√3=√3cos2x+sin2x=2sin ( 2x+ π).
3
所以函数f (x)的最小正周期T=π.
因为 (α π) 8,得 4,
(2) f − =2sinα= sinα=
2 6 5 5
3
又因为α是锐角,所以cosα= ,
5
12 5
因为α+β∈(0,π),且cos(α+β)=− ,所以sin(α+β)= ,
13 13
5 3 −12 4 63
所以sinβ=sin[(α+β)−α]=sin(α+β)cosα−cos(α+β)sinα= × − × = .
13 5 12 5 65
16.解:(1)由复数z=3+mi(i是虚数单位,m∈R),可得z=3−mi,
则z⋅(3+i)=(3−mi)(3+i)=9+m+(3−3m)i,
因为z⋅(3+i)是实数,所以3−3m=0,解得m=1,
第 页,共 页
6 1则 z = 1+2i =− 3 + 4 i ,所以 |z |= √ ( − 3) 2 + (4) 2 =1 .
1 1−2i 5 5 1 5 5
n−i2025 n−i (n−i)(3−i) (3n−1)+(−n−3)i
(2)解:由z = = = = ,
2 3+i 3+i 10 10
因为复数z 在复平面内对应的点在第二象限,可得3n−1<0且−n−3>0,
2
解得n<−3,所以实数n的取值范围为(−∞,−3).
17.解:(1)设圆锥的高为ℎ,
1
由题意得圆锥母线为10cm,
则 ,
ℎ
=√102−62=8cm
1
1
V =20π×62− π×62×8=624π≈1960cm3;
3
(2)圆柱的侧面积为2πr⋅20=240π,圆柱的上底面的面积为36π,
圆锥侧面积为S =60π.
锥侧
,
∴S =240π+36π+60π=336πcm2
总
336π×500×30
故总费用为 ≈1583(元).
104
18.解:(1)因为E为CD中点,
⃗ 1 ⃗ 1 ⃗ 1 ⃗ 1( ⃗ ⃗ ) 1 ⃗ 3 ⃗
所以AE= AD+ AC= AD+ AB+2AD = AB+ AD,
2 2 2 2 2 2
3 1
所以x+ y= + =2.
2 2
(2) 由 (1) 得| A ⃗ E | = √ (1 A ⃗ B+ 3 A ⃗ D ) 2 = √1 A ⃗ B2+ 9 A ⃗ D2+ 3 A ⃗ B⋅A ⃗ D
2 2 4 4 2
= √1 ×22+ 9 ×(√2) 2+ 3 ×2×√2× ( − √2) = √10,
4 4 2 2 2
第 页,共 页
7 1因为 ⃗ ⃗ ⃗ ,所以
BD=AD−AB
| B ⃗ D | = √ (A ⃗ D−A ⃗ B) 2= √ A ⃗ D2+A ⃗ B2−2A ⃗ B⋅A ⃗ D= √ (√2) 2+22−2×√2×2× ( − √2) =√10 ,
2
A ⃗ E⋅B ⃗ D= (1 A ⃗ B+ 3 A ⃗ D ) ⋅ ( A ⃗ D−A ⃗ B ) =− 1 A ⃗ B2−A ⃗ D A ⃗ B+ 3 A ⃗ D2=− 1 ×22−√2×2× ( − √2) + 3 ×(√2) 2=3
2 2 2 2 2 2 2
⃗ ⃗
⃗ ⃗ AE⋅BD 3
所以cos∠AFB=cos⟨ AE,BD⟩= =
.
| ⃗ || ⃗ | 5
AE BD
19.解:(1)由2c−b=2acosB和正弦定理得:2sinC−sinB=2sinAcosB,
即2sin(A+B)−sinB=2sin AcosB,
∴2cosAsinB−sinB=0,sinB(2cosA−1)=0,
1 π
又∵sinB≠0,∴cosA= ,∵A∈(0,π),∴A= .
2 3
.
(2)∵b2+c2−a2=2bccosA,∴3c=2bccosA=bc,∴b=3
⃗ 1( ⃗ ⃗ )
∵AD= AB+AC ,
2
⃗ 1( ⃗ ⃗ ⃗ ⃗ ) 1( ⃗ | ⃗ | ),
∴|AD|2= AB2+AC2+2AB⋅AC = |AB|2+3 AB +9
4 4
| ⃗ | √19 | ⃗ |
∵ AD = ,∴AB =2.
2
1 3√3
所以▵ABC的面积为S= bcsin A= .
2 2
( π) √3 1 √3 √3
sin C+ + sinC+ cosC+
(3)由正弦定理得:a+b sin A+sinB 3 2 2 2 2
= = =
c sinC sinC sinC
√3 √3 C
cosC+ 2cos2
2 2 1 √3 2 1 √3 1 1
= + = + = + .
sinC 2 2 C C 2 2 C 2
2sin cos tan
2 2 2
第 页,共 页
8 1π
{ 00且m⋅g(1)>0且Δ=1−48m>0且−1< <1,解得m<−1,
8m
综合 可知,实数 的取值范围是( 1),
①②③④ m −∞,−
2
所以 ( 1) (1) m 5 m 3 1 3,
f − +f = + + + =m+2<− +2=
2 2 2 4 2 4 2 2
故 ( 1) (1)的取值范围为( 3).
f − +f −∞,
2 2 2
解法 2 :由方程 −1=2 ( 2mc2− 1 c+1 ),可得 4mc2=c−3 ,
2
即方程4mc2=c−3在c∈(−1,1)上有解,
1 c2
当m=0时,方程无解,只需方程 = 在c∈(−1,1)上有解,
4m c−3
c2 (t+3) 2 9
令c−3=t(−4