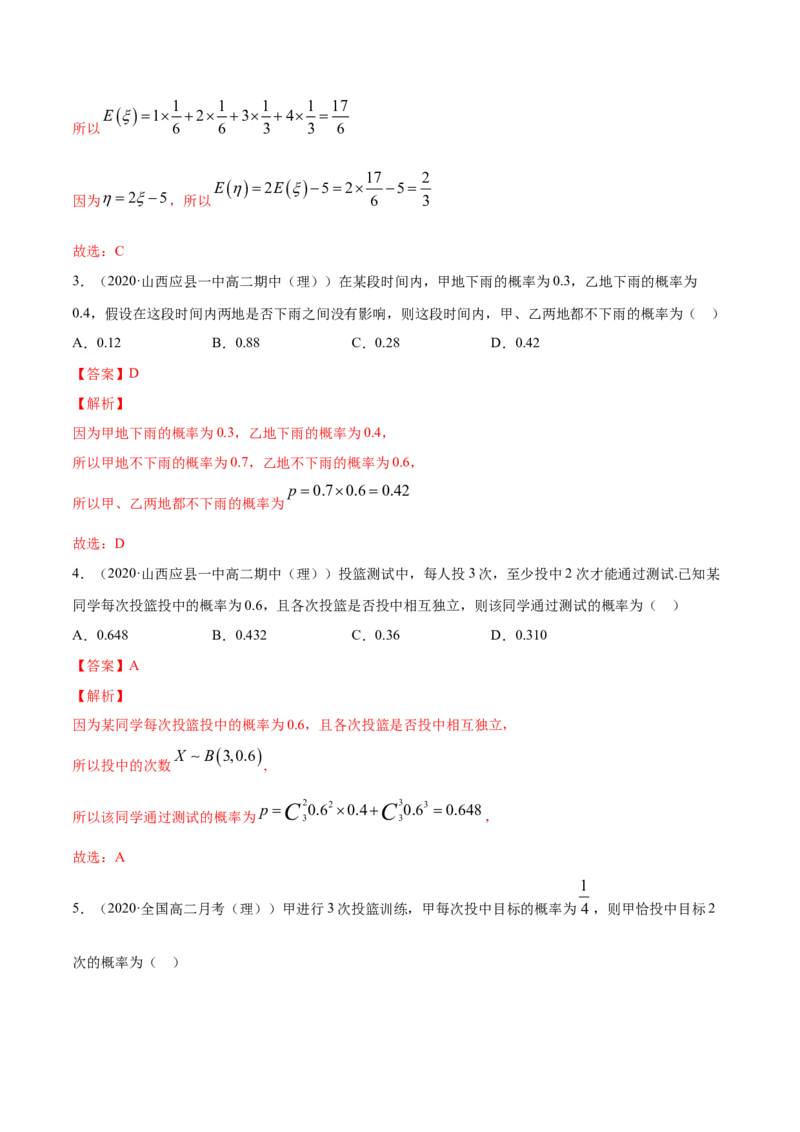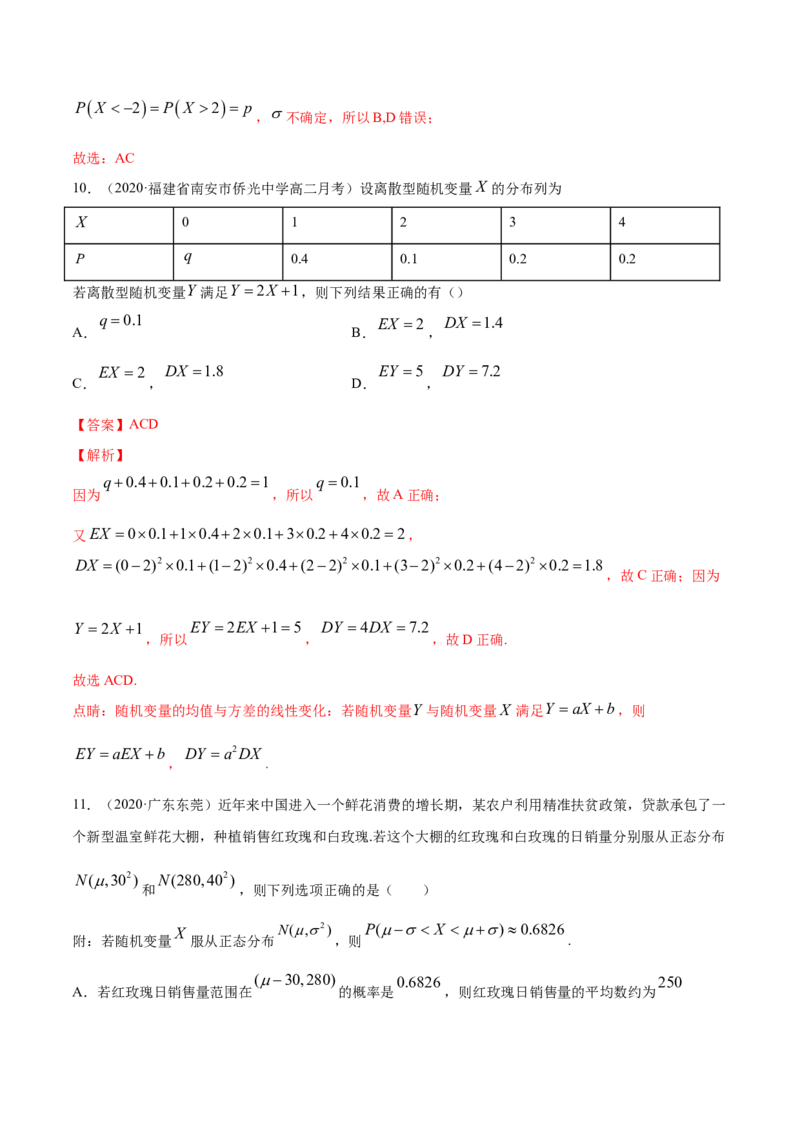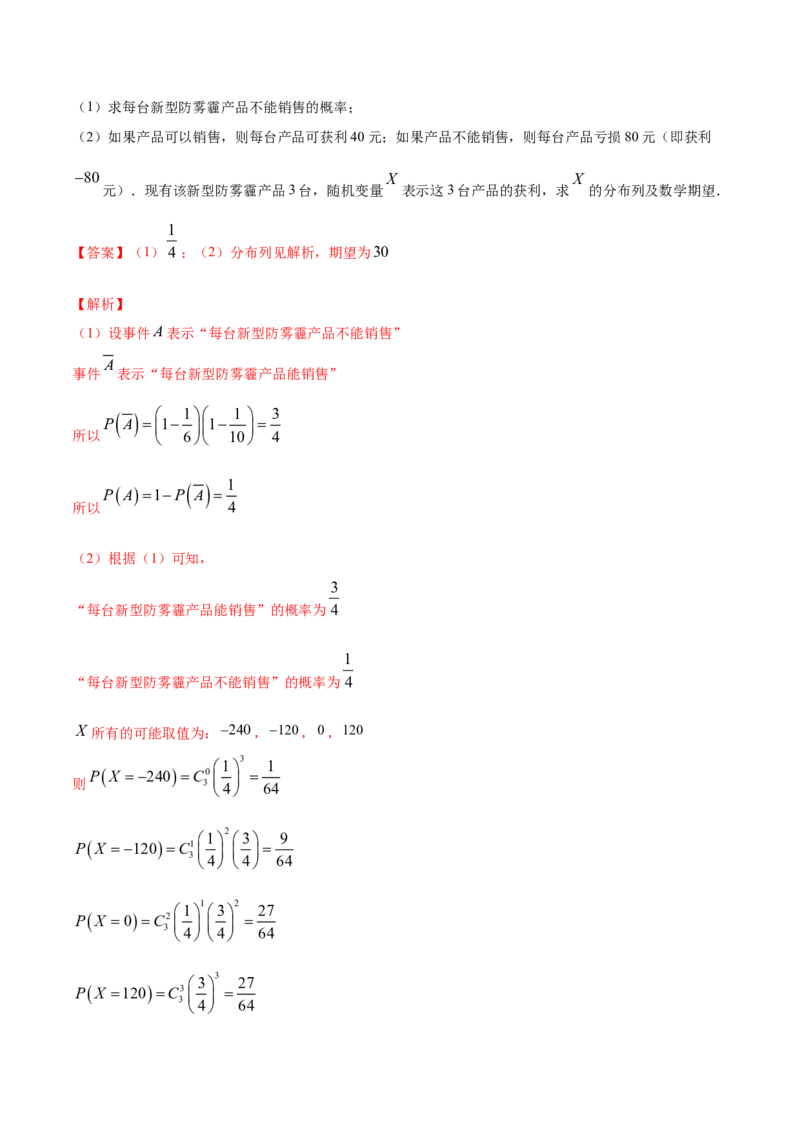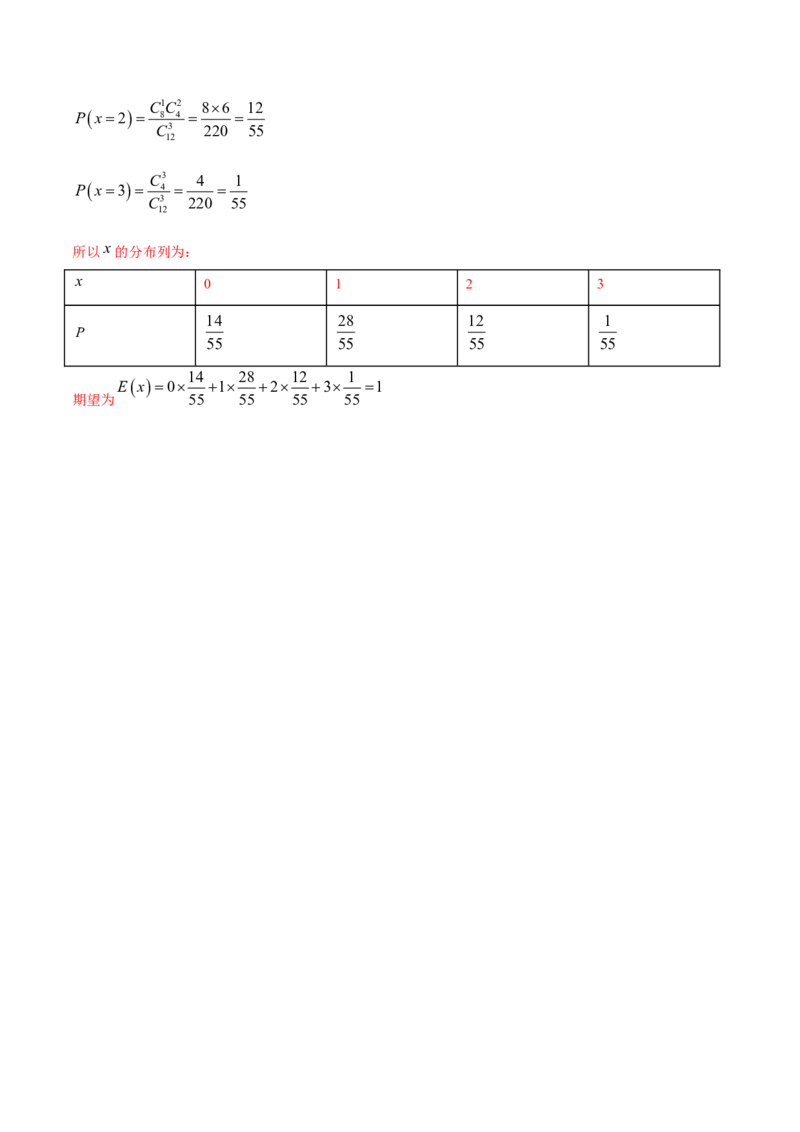专题35随机变量及其分布列（单元测试卷）（解析版）_E015高中全科试卷_数学试题_选修3_05.专项训练

专题35 《随机变量及其分布列》单元测试卷 一、单选题 1．（2020·山西应县一中高二期中（理））袋中装有大小和颜色均相同的5个乒乓球,分别标有数字 1,2,3,4,5,现从中任意抽取2个,设两个球上的数字之积为X,则X所有可能值的个数是( ) A．6 B．7 C．10 D．25 【答案】C 【解析】 2,3,4,5,6,8,10,12,15,20 10 列出所有可能取值如下表所示，由表格可知，所有可能取值为： 共 种.故选C. 1 2 3 4 5 1 2 3 4 5 2 2 6 8 10 3 3 6 12 15 4 4 8 12 20 5 5 10 15 20  2．（2020·青海西宁 高二期末（理））已知 的分布列为  1 2 3 4 1 1 1 P m 6 6 3 25 E 设 ，则 （ ） 1 1 2 3 A．2 B．3 C．3 D．2 【答案】C 【解析】 1 1 1 1   m1 m 由分布列的性质可得：6 6 3 ，解得 31 1 1 1 17 E1 2 3 4  所以 6 6 3 3 6 17 2 E2E52 5 因为25，所以 6 3 故选：C 3．（2020·山西应县一中高二期中（理））在某段时间内，甲地下雨的概率为0.3，乙地下雨的概率为 0.4，假设在这段时间内两地是否下雨之间没有影响，则这段时间内，甲、乙两地都不下雨的概率为（ ） A．0.12 B．0.88 C．0.28 D．0.42 【答案】D 【解析】 因为甲地下雨的概率为0.3，乙地下雨的概率为0.4， 所以甲地不下雨的概率为0.7，乙地不下雨的概率为0.6， p 0.70.60.42 所以甲、乙两地都不下雨的概率为 故选：D 4．（2020·山西应县一中高二期中（理））投篮测试中，每人投3次，至少投中2次才能通过测试.已知某 同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（ ） A．0.648 B．0.432 C．0.36 D．0.310 【答案】A 【解析】 因为某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立， X B3,0.6  所以投中的次数 , pC2 0.620.4C3 0.63 0.648 所以该同学通过测试的概率为 3 3 ， 故选：A 1 5．（2020·全国高二月考（理））甲进行3次投篮训练，甲每次投中目标的概率为4 ，则甲恰投中目标2 次的概率为（ ）9 27 9 27 A．64 B．64 C．16 D．128 【答案】A 【解析】 2 1 3 9 PC2  甲恰投中目标2次的概率为 3  4   4 64 . 故选：A. 3 m 6．（2020·营口市第二高级中学高二期末）从装有除颜色外完全相同的 个白球和 个黑球的布袋中随机 EX3 摸取一球，有放回地摸取 6 次，设摸得黑球的个数为X ，已知 ，则 m 等于（ ） 2 1 3 5 A． B． C． D． 【答案】C 【解析】 3 m 3 P(X k)Ck( )k( )mk X B(6, ) 根据题意可得出 6 3m 3m ，即 3m 3 EX6 3m3 所以 3m 故选C 8  B(10, 0.4) E() D()  7．（2020·辽宁沈阳 高二期中）已知随机变量 ，若 ，则 ， 分别是( ) A．4和2.4 B．2和2.4 C．6和2.4 D．4和5.6 【答案】A 【解析】 ～B（10，0.4），E100.44，D100.40.62.4，  8，E E（8）4，D D（8）2.4  故选A．1,2,3,4,5 2 A 2 8．（2020·营口市第二高级中学高二期末）从 中任取 个不同的数，事件 “取到的 个数之 PB| A 和为偶数”，事件B“取到两个数均为偶数”，则 ( ) 1 1 2 1 A．8 B．4 C．5 D．2 【答案】B 【解析】 1 PAB 10 1 依题意 PA C 3 2 C 2 2  4  2 , PAB= C 2 2  1 ,故 PA  2  4 .故选B. C2 10 5 C2 10 PB| A 5 5 5 二、多选题 N(,2) 3,1 9．（2020·山东奎文 潍坊中学高二期中）设随机变量X服从正态分布 ，且X落在区间 内 1,3 PX 2 p 的概率和落在区间 内的概率相等.若 ，则下列结论正确的有（ ） 0 2 A． B． 1 P(0 X 2)  p PX  21 p C． 2 D． 【答案】AC 【解析】 N(,2) x 3,1 1,3 因为正态分布 关于 对称，又X落在区间 内的概率和落在区间 内的概率相等， 0 所以 ，A正确； N(,2) x 因为正态分布 关于 对称， 1 1 P(X 0) P(0 X 2) P(X 0)P(X 2)  p 所以 2 2 ，C正确；PX 2 PX 2 p  ， 不确定，所以B,D错误； 故选：AC 10．（2020·福建省南安市侨光中学高二月考）设离散型随机变量X 的分布列为 X 0 1 2 3 4 q P 0.4 0.1 0.2 0.2 若离散型随机变量Y 满足Y 2X 1，则下列结果正确的有（） q 0.1 EX 2 DX 1.4 A． B． ， EX 2 DX 1.8 EY 5 DY 7.2 C． ， D． ， 【答案】ACD 【解析】 q0.40.10.20.21 q 0.1 因为 ，所以 ，故A正确； 又EX 00.110.420.130.240.22， DX (02)20.1(12)20.4(22)20.1(32)20.2(42)20.21.8 ，故C正确；因为 Y 2X 1 EY 2EX 15 DY 4DX 7.2 ，所以 ， ，故D正确. 故选ACD. 点睛：随机变量的均值与方差的线性变化：若随机变量Y 与随机变量X 满足Y aX b，则 EY aEX b DY a2DX ， . 11．（2020·广东东莞）近年来中国进入一个鲜花消费的增长期，某农户利用精准扶贫政策，贷款承包了一 个新型温室鲜花大棚，种植销售红玫瑰和白玫瑰.若这个大棚的红玫瑰和白玫瑰的日销量分别服从正态分布 N(,302) N(280,402) 和 ，则下列选项正确的是（ ） X N(,2) P( X )0.6826 附：若随机变量 服从正态分布 ，则 . (30,280) 0.6826 250 A．若红玫瑰日销售量范围在 的概率是 ，则红玫瑰日销售量的平均数约为B．红玫瑰日销售量比白玫瑰日销售量更集中 C．白玫瑰日销售量比红玫瑰日销售量更集中 (280,320) 0.3413 D．白玫瑰日销售量范围在 的概率约为 【答案】ABD 【解析】 +30=280，=250 对于选项A： ，正确；  30 40 对于选项B C：利用 越小越集中， 小于 ，B正确，C不正确； 1 P( X )0.6826 0.3413 对于选项D：P(280 X 320)= 2 ，正确. 故选：ABD. 6 4 12．（2020·山东省招远第一中学高二月考）某班级的全体学生平均分成 个小组，且每个小组均有 名男 6 生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动，若抽取的 名学生中至少有一名男生 728 的概率为729，则（ ） 36 A．该班级共有 名学生 2 B．第一小组的男生甲被抽去参加社区服务的概率为3 160 C．抽取的6名学生中男女生数量相同的概率是729 4 DX D．设抽取的6名学生中女生数量为X ，则 3 【答案】ACD 【解析】 n 设该班级每个小组共有 名女生，728 ∵抽取的6名学生中至少有一名男生的概率为729， 728 1 1  ∴抽取的6名学生中没有男生（即6名学生全为女生）的概率为 729 729， 6 6  n  1 1   ∴    ，解得 ， n4 729 3 n2 ∴每个小组有4名男生、2名女生，共6名学生， ∴该班级共有36名学生，则A对； 1 ∴第一小组的男生甲被抽去参加社区服务的概率为6，则B错； 3 3 4 2 160 C3   抽取的 6 名学生中男女生数量相同的概率是 6  6    6   729 ，则C对；  1 1  1 4 X B 6, DX6  1       设抽取的6名学生中女生数量为 X ，则  3，则 3  3 3 ，则D对； 故选：ACD． 三、填空题 a Pk 13．（2020·通榆县第一中学校高二期末（理））已知随机变量的分布列为 2k1 ，其中k 1， a  2，3，4，5，则 _______． 16 【答案】31 【解析】 a a a a a     1 由题意知，20 21 22 23 24 ， 1 1 25 a 1 ， 1 1 216 a  解得 31， 16 故答案为：31. X ~ B(6,0.4) 2X 1 D() 14．（2020·安徽黄山 高二期末（理））已知随机变量 ，则当 时， =_________． 【答案】5.76 【解析】 X ~ B(6,0.4) D(X)60.40.61.44 因为 ，所以 ， 2X 1 D()4DX 41.445.76 又因为 ，所以 ， 5.76 故答案为： . 15．（2019·江西新余 高二期末（文））甲、乙、丙三人将独立参加某项体育达标测试.根据平时训练的经 验，甲、乙、丙三人能达标 3 2 3 的概率分别为4 、3 、5 ，则三人中有人达标但没有全部达标的概率为_______. 2 【答案】3 【解析】 3 2 3 1 1 2 2 2 1       因三人中有一人或两人达标，其概率为 4 3 5 4 3 5 3 ,故应填3 . 16．（2020·河北邢台 高二期中）设随机变量X 的分布列如下： X 0 1 2 1 1 1 P 2p  p  p 3 3 31 p E  X  DX 若 5 ，则 的最大值是___________， 的最大值是___________. 2 38 【答案】5 75 【解析】  1 1 0  p ,  3 3   1 0 p , ①由题意可得 3   1 p ,   5 1 1  p 解得5 3.  1 1  1  2 EX0 2p 1  p 2  p 13p�       因为  3 3  3  5， 2 EX 所以 的最大值是5 ，  1 1 1  DX[0(13p)]2 2p [1(13p)]2  p)[2(13p)]2  p      ②因为  3 3 3  2 9p2  p 3 ， 1 1 38  p DX 因为5 3，所以 75， 38 DX . 所以 的最大值是75 五、解答题 17．（2020·绥德中学高二月考（理））袋中有20个大小相同的球，其中标号为0的有10个，标号为n的有n个（n =1,2,3,4）.现从袋中任取一球，X表示所取球的标号.求X的分布列、数学期望和方差. 【答案】详见解析 【解析】 10 1 1 2 1 3 PX 0  PX 1 PX 2  PX 3 20 2， 20， 20 10， 20 ， 4 1 PX 4  20 5. X 的分布列为 X 0 1 2 3 4 1 1 1 3 1 P 2 20 10 20 5 1 1 1 3 1 EX0 1 2 3 4 1.5 ∴ 2 20 10 20 5 ， 1 1 3 1 DX01.52  11.52  21.52  31.52  2.75 2 20 20 5 . 18．（2019·武威第五中学高二期末（理））有20件产品，其中5件是次品，其余都是合格品，现不放回 的从中依次抽2件.求: （1）第一次抽到次品的概率； （2）在第一次抽到次品的条件下，第二次抽到次品的概率. 1 4 【答案】（1）4 （2）19 【解析】 设第一次抽到次品的事件为A，第二次抽到次品的事件为B. （1）因为有20件产品，其中5件是次品，抽到每件产品的可能性相同，所以第一次抽到次品的概率为 5 1 PA  20 4. 19 4 （2）第一次抽到次品后，剩余 件产品，其中有 件次品，又因为抽到每件产品的可能性相同，所以在4 PB| A 第一次抽到次品的条件下，第二次抽到次品的概率为 19 . 19．（2020·全国高三课时练习（理））现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加 者选择.为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1 或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏. （Ⅰ）求这4个人中恰有2人去参加甲游戏的概率； （Ⅱ）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率； （Ⅲ）用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记 ，求随机变量 的分布列与 数学期望 . 8 1 148 E() 【答案】（1）27 （2）9（3） 81 【解析】 1 2 依题意，这4个人中，每个人去参加甲游戏的概率为3，去参加乙游戏的概率为3 .设“这4个人中恰有i人 去参加甲游戏”为事件 (i＝0,1,2,3,4)，则 （Ⅰ）这4个人中恰有2人去参加甲游戏的概率 （Ⅱ）设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B，则 ， 由于 与 互斥，故 1 所以，这4个人去参加甲游戏的人数大于去参加乙游戏的人数的概率为9 （Ⅲ）ξ的所有可能取值为0,2,4.由于 与 互斥， 与 互斥，故， ． 所以ξ的分布列是 ξ 0 2 4 8 40 17 P 27 81 81 随机变量ξ的数学期望 20．（2020·四川省南充市第一中学高二期中（理））某学校高三年级有400名学生参加某项体育测试，根 据男女学生人数比例，使用分层抽样的方法从中抽取了100名学生，记录他们的分数，将数据分成7组： [30,40),[40,50), [90,100]  ，整理得到如下频率分布直方图： （1）若该样本中男生有55人，试估计该学校高三年级女生总人数； （2）若规定小于60分为“不及格”，从该学校高三年级学生中随机抽取一人，估计该学生不及格的概率； [80,90) 90,100 （3）若规定分数在 为“良好”, 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望. 180 0.1 【答案】（1） 人（2） （3）详见解析 【解析】 （1）∵样本中男生有55人,则女生45人 45 400 180 ∴估计总体中女生人数 100 人 A （2）设“不及格”为事件A,则“及格”为事件 P(A)1P(A)1(0.20.40.20.1)0.1 ∴ P(B)0.20.10.3 （3）设“样本中“良好”或“优秀””为事件B,则 X ~ B(3,0.3) 依题意可知： P(B 0)0.73 P(X 1)C10.310.72 , 3 P(X 2)C20.320.71, P(X 3)0.33 3 所以,X的分布列为 X 0 1 2 3 P 0.343 0.441 0.189 0.027 E(X)np 30.30.9 21．（2020·北京市十一学校高三月考（理））为降低雾霾等恶劣气候对居民的影响，某公司研发了一种新 型防雾霾产品．每一台新产品在进入市场前都必须进行两种不同的检测，只有两种检测都合格才能进行销 1 售，否则不能销售．已知该新型防雾霾产品第一种检测不合格的概率为6，第二种检测不合格的概率为 1 10，两种检测是否合格相互独立．（1）求每台新型防雾霾产品不能销售的概率； （2）如果产品可以销售，则每台产品可获利40元；如果产品不能销售，则每台产品亏损80元（即获利 80 X X 元）．现有该新型防雾霾产品3台，随机变量 表示这3台产品的获利，求 的分布列及数学期望． 1 【答案】（1）4 ；（2）分布列见解析，期望为30 【解析】 （1）设事件A表示“每台新型防雾霾产品不能销售” A 事件 表示“每台新型防雾霾产品能销售”    1 1  3 P A  1 1     所以  6 10 4 PA1P  A   1 所以 4 （2）根据（1）可知， 3 “每台新型防雾霾产品能销售”的概率为4 1 “每台新型防雾霾产品不能销售”的概率为4 X 所有的可能取值为：240，120，0，120 3 1 1 PX 240C0  则 3  4   64 2 1 3 9 PX 120C1      3 4 4 64 1 2 1 3 27 PX 0C2      3 4 4 64 3 3 27 PX 120C3    3 4 64所以X 的分布列为 X 240 120 0 120 1 9 27 27 P 64 64 64 64 1 9 27 EX 240 120 120 所以 64 64 64 则EX 30 22．（2020·永安市第三中学高二期中）2018年茂名市举办“好心杯”少年美术书法作品比赛，某赛区收 到200件参赛作品，为了解作品质量，现从这些作品中随机抽取12件作品进行试评.成绩如下： 67,82,78,86,96,81,73,84,76,59,85,93. （1）求该样本的中位数和方差； （2）若把成绩不低于85分（含85分）的作品认为为优秀作品，现在从这12件作品中任意抽取3件，求 抽到优秀作品的件数的分布列和期望. 【答案】（1）中位数为81.5，方差为98.83（2）详见解析 【解析】 （1）样本数据按顺序为59，67,73,76,78,81,82,84,85,86,93,96. 8182 81.5 数据的中位数为： 2 596773767881828485869396 x  80 平均数为 12 方差为 1 1186 S2    212 132 72 42 221222425262132162  98.83 12 12 x x （2）设抽到优秀作品的个数为 ，则 的可能值为0,1，2,3 C3 56 14 Px0 8   C3 220 55 12 C2C1 284 28 Px1 8 4   C3 220 55 12C1C2 86 12 Px2 8 4   C3 220 55 12 C3 4 1 Px3 4   C3 220 55 12 x 所以 的分布列为： x 0 1 2 3 14 28 12 1 P 55 55 55 55 14 28 12 1 Ex0 1 2 3 1 期望为 55 55 55 55