专题38成对数据的统计分析（单元测试卷）原卷版_E015高中全科试卷_数学试题_选修3_05.专项训练_专题38成对数据的统计分析（单元测试卷）

专题38 《成对数据的统计分析》单元测试卷 一、单选题 1．（2020·甘肃省会宁县第二中学期中（文））某商品销售量y（件）与销售价格x（元/件）负相关，则 其回归方程可能是（ ） yˆ 10x200 yˆ 10x200 A． B． yˆ 10x200 yˆ 10x200 C． D． 2．（2020·福建湖里·厦门双十中学高二期中）在一组样本数据 (x 1， y 1 ) ， (x 2， y 2 ) ，  ， (x n， y n )(n�2 ， 1 y  x2 x 1 ， x 2 ， x n 不全相等）的散点图中，若所有样本点 x 2 ，y i )(i1，2，，n)都在直线 3 上， 则这组样本数据的样本相关系数为（ ） 1  A．1 B．0 C． 3 D．1 3．（2020·福建湖里·厦门双十中学高二期中）已知四个命题： R2 R2 ①在回归分析中， 可以用来刻画回归效果， 的值越大，模型的拟合效果越好； K2 ②在独立性检验中，随机变量 的值越大，说明两个分类变量有关系的可能性越大； y 0.2x12 x y ③在回归方程 中，当解释变量 每增加1个单位时，预报变量 平均增加1个单位； ④两个随机变量相关性越弱，则相关系数的绝对值越接近于1； 其中真命题是： A．①④ B．②④ C．①② D．②③ 4．（2020·河南南阳·期末（理））利用独立性检验的方法调查高中性别与爱好某项运动是否有关，通 过随机调查200名高中生是否爱好某项运动，利用2×2列联表，由计算可得K2≈7.245，参照下表：得到 的正确结论是（ ） P（K2 k） 0.01 0.05 0.025 0.010 0.005 0.001 0k 2.706 3.841 5.024 6.635 7.879 10.828 0 A．有99%以上的把握认为“爱好该项运动与性别无关” B．有99%以上的把握认为“爱好该项运动与性别有关”、 C．在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关” D．在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关” 5．（2020·四川邻水实验学校开学考试（理））在一次独立性检验中得到如下列联表： A A 总计 1 2 B 200 800 1000 1 B 180 a 180＋a 2 总计 380 800＋a 1180＋a 若这两个分类变量A和B没有关系，则a的可能值是( ) A．200 B．720 C．100 D．180 6．（2020·赣州市赣县第三中学月考（文））某市政府在调查市民收入增减与旅游愿望的关系时，采用 K2 k 6.023 独立性检验法抽查了3000人，计算发现 的观测值 ，根据这一数据查阅表，市政府断言“市民 收入增减与旅游愿望有关系”这一断言犯错误的概率不超过（ ） P  K2 k  0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0 k 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 0 A．0.005 B．0.025 C．0.05 D．0.1 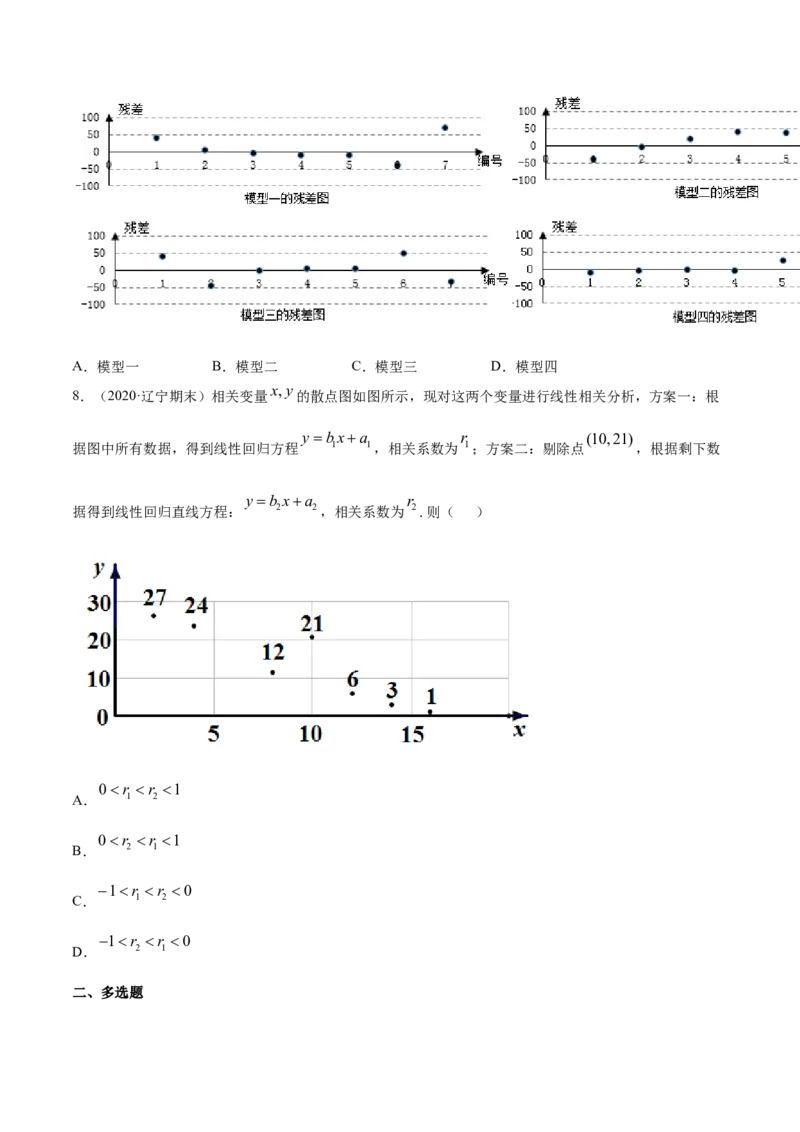7．（2020·福建期末）红铃虫是棉花的主要害虫之一，一只红铃虫的产卵数和温度有关.现收集了7组观侧 数据.用4种模型分别进行拟合.由此得到相应的回归方程并进行残差分析，进一步得到如图4幅残差图，根 据残差图，拟合效果最好的模型是（ ）A．模型一 B．模型二 C．模型三 D．模型四 x,y 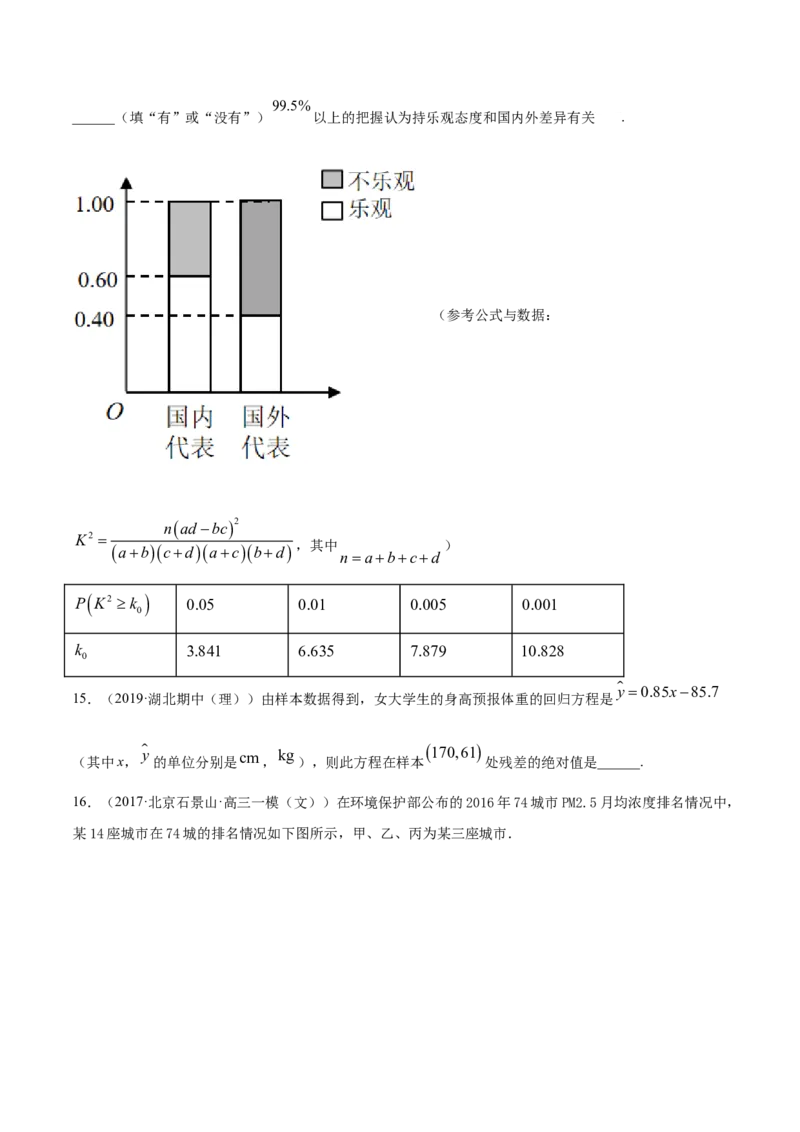8．（2020·辽宁期末）相关变量 的散点图如图所示，现对这两个变量进行线性相关分析，方案一：根 y bxa r (10,21) 据图中所有数据，得到线性回归方程 1 1，相关系数为 1；方案二：剔除点 ，根据剩下数 y b xa r 据得到线性回归直线方程： 2 2，相关系数为 2.则（ ） 0r r 1 A． 1 2 0r r 1 B． 2 1 1r r 0 C． 1 2 1r r 0 D． 2 1 二、多选题22 K2 9．（2020·山东省招远第一中学高二月考）某课外兴趣小组通过随机调查，利用 残联表和 统计量 P  K2 6.635  0.010 研究数学成绩优秀是否与性别有关.计算得K2 6.748，经查阅临界值表知 ，则 下列判断正确的是（ ） 100 1 A．每 个数学成绩优秀的人当中就会有 名是女生 0.010 B．若某人数学成绩优秀，那么他为男生的概率是 99% C．有 的把握认为“数学成绩优秀与性别有关” 1% D．在犯错误的概率不超过 的前提下认为“数学成绩优秀与性别有关” 10．（2020·南京市秦淮中学开学考试）为了对变量 x 与 y 的线性相关性进行检验，由样本点 x 1 ,y 1  、 x ,y  x ,y  2 2 、、 10 10 求得两个变量的样本相关系数为r，那么下面说法中错误的有（ ） y 2x1 r 1 A．若所有样本点都在直线 上，则 y 2x1 r 2 B．若所有样本点都在直线 上，则 r x y C．若 越大，则变量 与 的线性相关性越强 r x y D．若 越小，则变量 与 的线性相关性越强 11．（2020·广东梅州·高二期末）针对时下的“抖音热”，某校团委对“学生性别和喜欢抖音是否有关 4 “作了一次调查，其中被调查的男女生人数相同，男生喜欢抖音的人数占男生人数的5 ，女生喜欢抖音的 3 人数占女生人数5，若有95%的把握认为是否喜欢抖音和性别有关，则调查人数中男生可能有（ ）人 附表：P  K2 k  0.100 0.050 0.010 0.005 0.001 k 2.706 3.841 6.635 7.879 10.828 n(ad bc)2 K2  附： (ab)(cd)(ac)(bd) A．25 B．35 C．45 D．60 12．（2020·广东南海·期末）某种产品的广告支出费用x（单位：万元）与销售量y（单位：万件）之间 的对应数据如下表所示： 广告支出费用x 2.2 2.6 4.0 5.3 5.9 销售量y 3.8 5.4 7.0 11.6 12.2 y 2.27xa R2 0.96 根据表中的数据可得回归直线方程 ， ，以下说法正确的是（ ）  A．第三个样本点对应的残差e 1 3 B．在该回归模型对应的残差图中，残差点比较均匀地分布在倾斜的带状区域中 C．销售量的多少有96%是由广告支出费用引起的 D．用该回归方程可以比较准确地预测广告费用为20万元时的销售量 三、填空题 13．（2020·吉林高二期末（文））某次国际会议为了搞好对外宣传工作，会务组选聘了50名记者担任对 22 abd  外翻译工作，在如表“性别与会外语”的 列联表中， ___________. 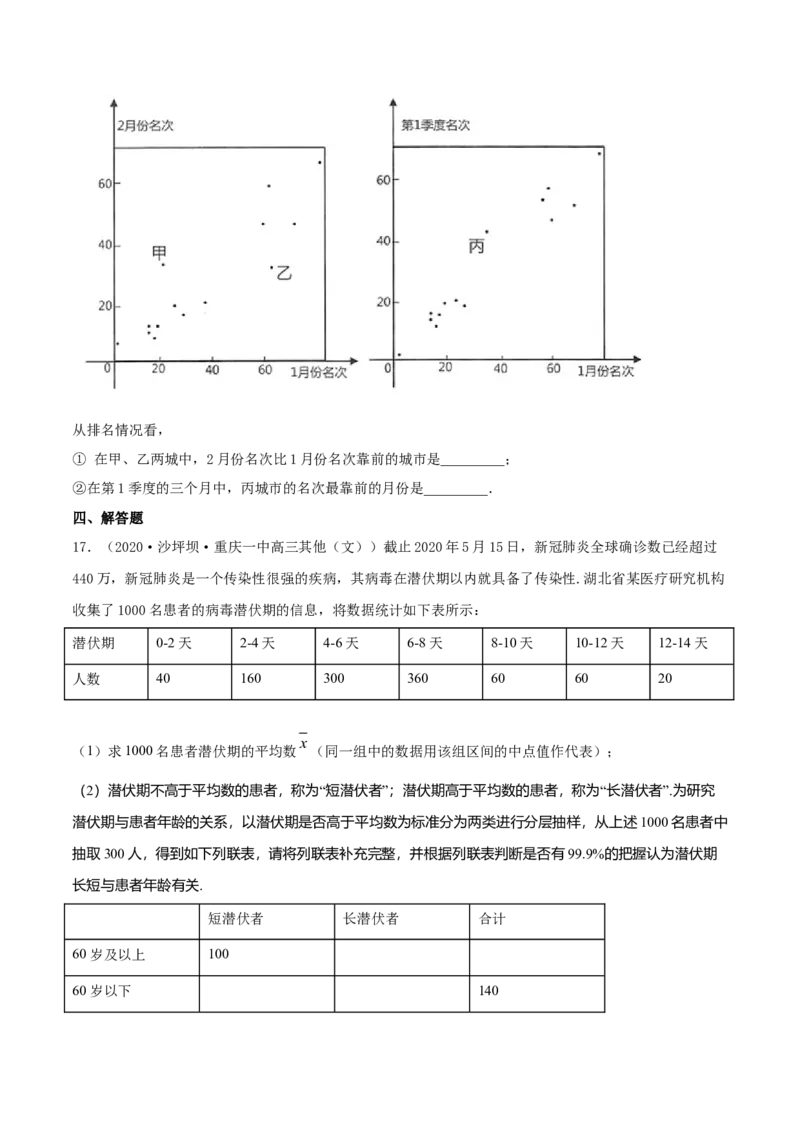会外语 不会外语 总计 男 a b 20 女 6 d 总计 18 50 14．（2020·湖南期末）某手机运营商为了拓展业务，现对该手机使用潜在客户进行调查，随机抽取国内国 100 外潜在用户代表各 名，调查用户对是否使用该手机的态度，得到如图所示的等高条形图.根据等高图，99.5% ______（填“有”或“没有”） 以上的把握认为持乐观态度和国内外差异有关 . （参考公式与数据： nad bc2 K2  ，其中 ） abcdacbd nabcd P  K2 k  0.05 0.01 0.005 0.001 0 k 3.841 6.635 7.879 10.828 0 y 0.85x85.7 15．（2019·湖北期中（理））由样本数据得到，女大学生的身高预报体重的回归方程是 y cm kg 170,61 （其中x， 的单位分别是 ， ），则此方程在样本 处残差的绝对值是______. 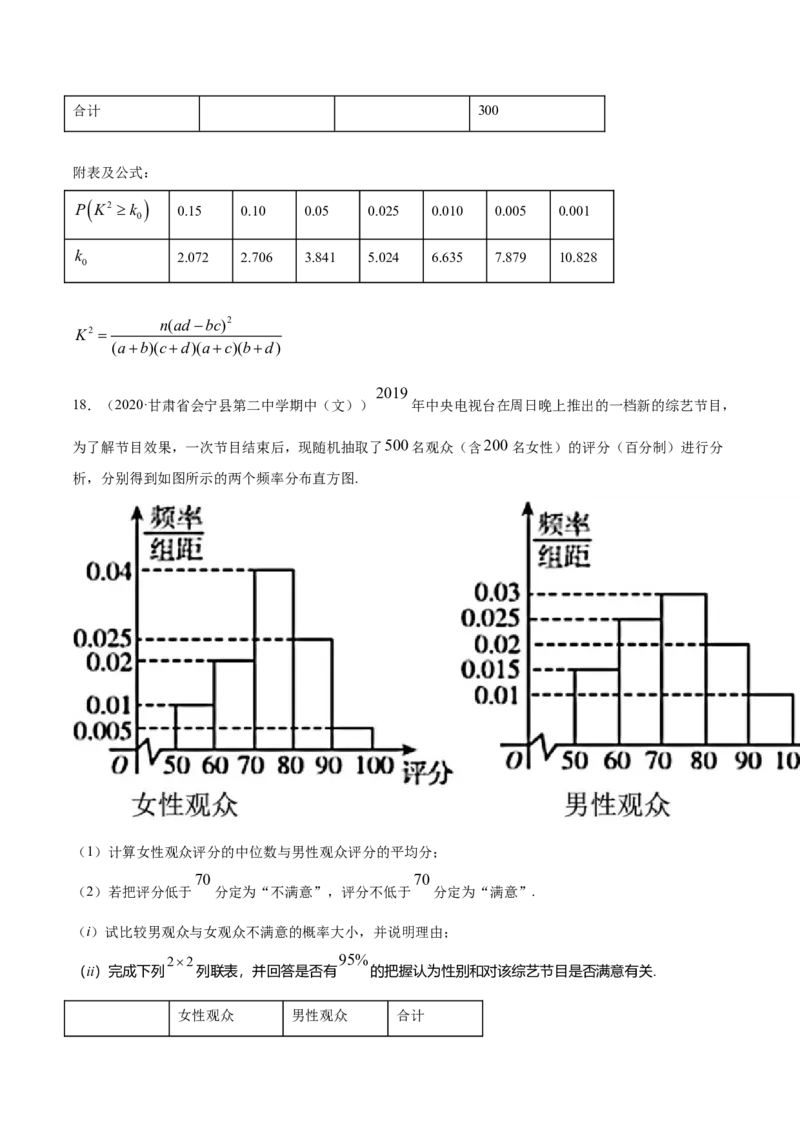16．（2017·北京石景山·高三一模（文））在环境保护部公布的2016年74城市PM2.5月均浓度排名情况中， 某14座城市在74城的排名情况如下图所示，甲、乙、丙为某三座城市．从排名情况看， ① 在甲、乙两城中，2月份名次比1月份名次靠前的城市是_________； ②在第1季度的三个月中，丙城市的名次最靠前的月份是_________． 四、解答题 17．（2020·沙坪坝·重庆一中高三其他（文））截止2020年5月15日，新冠肺炎全球确诊数已经超过 440万，新冠肺炎是一个传染性很强的疾病，其病毒在潜伏期以内就具备了传染性.湖北省某医疗研究机构 收集了1000名患者的病毒潜伏期的信息，将数据统计如下表所示： 潜伏期 0-2天 2-4天 4-6天 6-8天 8-10天 10-12天 12-14天 人数 40 160 300 360 60 60 20 x （1）求1000名患者潜伏期的平均数 （同一组中的数据用该组区间的中点值作代表）； （2）潜伏期不高于平均数的患者，称为“短潜伏者”；潜伏期高于平均数的患者，称为“长潜伏者”.为研究 潜伏期与患者年龄的关系，以潜伏期是否高于平均数为标准分为两类进行分层抽样，从上述1000名患者中 抽取300人，得到如下列联表，请将列联表补充完整，并根据列联表判断是否有99.9%的把握认为潜伏期 长短与患者年龄有关. 短潜伏者 长潜伏者 合计 60岁及以上 100 60岁以下 140合计 300 附表及公式： P  K2 k  0.15 0.10 0.05 0.025 0.010 0.005 0.001 0 k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 0 n(ad bc)2 K2  (ab)(cd)(ac)(bd) 2019 18．（2020·甘肃省会宁县第二中学期中（文）） 年中央电视台在周日晚上推出的一档新的综艺节目， 为了解节目效果，一次节目结束后，现随机抽取了500名观众（含200名女性）的评分（百分制）进行分 析，分别得到如图所示的两个频率分布直方图. （1）计算女性观众评分的中位数与男性观众评分的平均分； 70 70 （2）若把评分低于 分定为“不满意”，评分不低于 分定为“满意”. （i）试比较男观众与女观众不满意的概率大小，并说明理由； 22 95% （ii）完成下列 列联表，并回答是否有 的把握认为性别和对该综艺节目是否满意有关. 女性观众 男性观众 合计“满意” “不满意” 合计 n(ad bc)2 K2  参考数据： (ab)(cd)(ac)(bd) P  K2 k  0.05 0.010 0.001 k 3.841 6.635 10.828 19．（2019·扶风县法门高中月考（文））下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产 量x（吨）与相应的生产能耗 y （吨标准煤）的几组对照数据 x 3 4 5 6 y 2.5 3.5 4 5 ˆ y x yˆ bxaˆ （1）请根据上表提供的数据，用最小二乘法求出 关于 的线性回归方程 ； （2）已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据（1）求出的线性回归方程，预测生产 100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？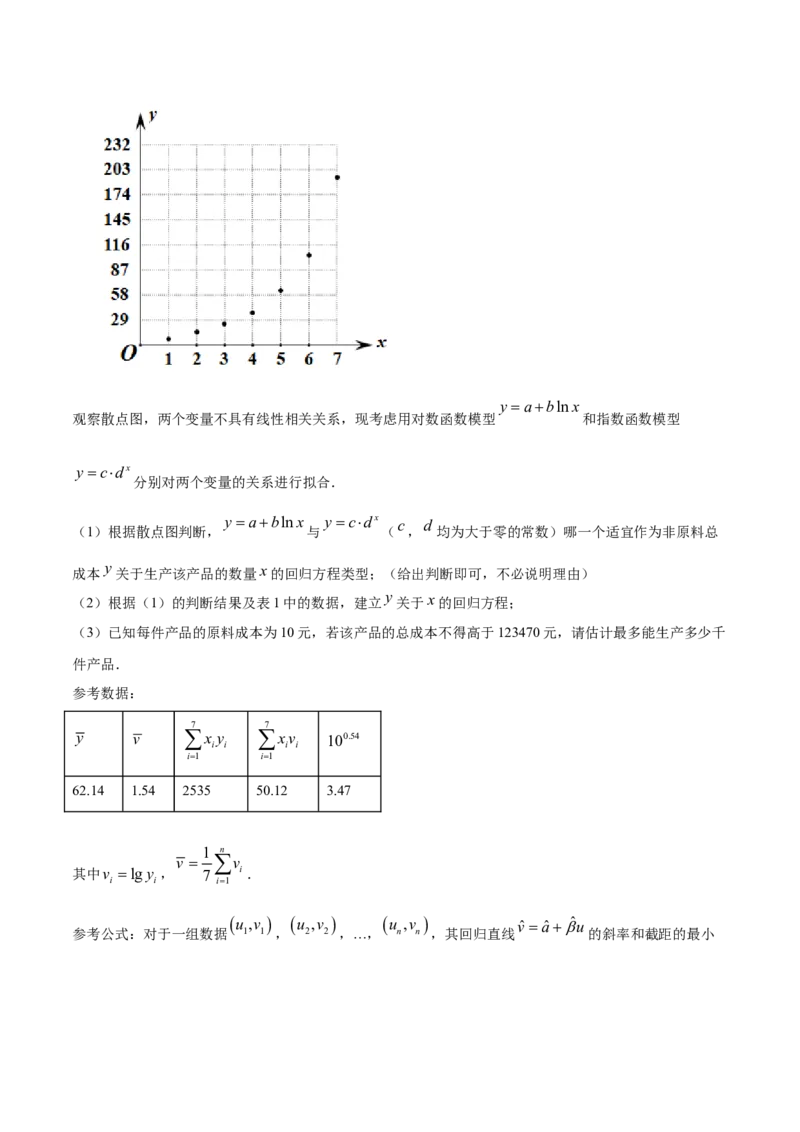 20．（2020·江苏广陵·扬州中学开学考试）某企业新研发了一种产品，产品的成本由原料成本及非原料 成本组成．每批产品的非原料总成本 y （元）与生产该产品的数量x（千件）有关，经统计得到如下数据： x 1 2 3 4 5 6 7 y 6 11 21 34 66 101 196 根据以上数据，绘制如图所示的散点图．y ablnx 观察散点图，两个变量不具有线性相关关系，现考虑用对数函数模型 和指数函数模型 y cdx 分别对两个变量的关系进行拟合． y ablnx y cdx c d （1）根据散点图判断， 与 （ ， 均为大于零的常数）哪一个适宜作为非原料总 成本 y 关于生产该产品的数量x的回归方程类型；（给出判断即可，不必说明理由） （2）根据（1）的判断结果及表1中的数据，建立 y 关于x的回归方程； （3）已知每件产品的原料成本为10元，若该产品的总成本不得高于123470元，请估计最多能生产多少千 件产品． 参考数据： 7 7 y v x y xv 100.54 i i i i i1 i1 62.14 1.54 2535 50.12 3.47 1 n v  v 其中v lgy ， 7 i ． i i i1 u ,v  u ,v  u ,v  vˆ aˆ ˆ u 参考公式：对于一组数据 1 1 ， 2 2 ，…， n n ，其回归直线 的斜率和截距的最小n uv nuv i i  ˆ  i1 二乘估计公式分别为 n ， ． u2 nu2 i aˆ v  ˆ u i1 21．（2020·四川武侯·成都七中高三开学考试（理））某厂生产不同规格的一种产品，根据检测标准， yg x(mm) ycxb 其合格产品的质量 与尺寸 之间近似满足关系式 （b，c为大于0的常数）.按照某指 (0.302,0.388) 标测定，当产品质量与尺寸的比在区间 内时为优等品.现随机抽取6件合格产品，测得数据 如下： 尺寸x(mm) 38 48 58 68 78 88 质量y(g) 16.8 18.8 20.7 22.4 24 25.5 y 质量与尺寸的比 0.442 0.392 0.357 0.329 0.308 0.290 x （1）现从抽取的6件合格产品中再任选2件，求选中的2件均为优等品的概率； （2）根据测得数据作了初步处理，得相关统计量的值如下表： 6 6 6 6 lnx ln y  lnx  lny  lnx 2 i i i i i i1 i1 i1 i1 75.3 24.6 18.3 101.4 根据所给统计量，求y关于x的回归方程. v ,u (i 1,2, ,6) 附：对于样本 i i  ，其回归直线ubva的斜率和截距的最小二乘法估计公式分别为： n n v vu u vu nvu i i i i ˆ b i1  i1 n n ， ， . 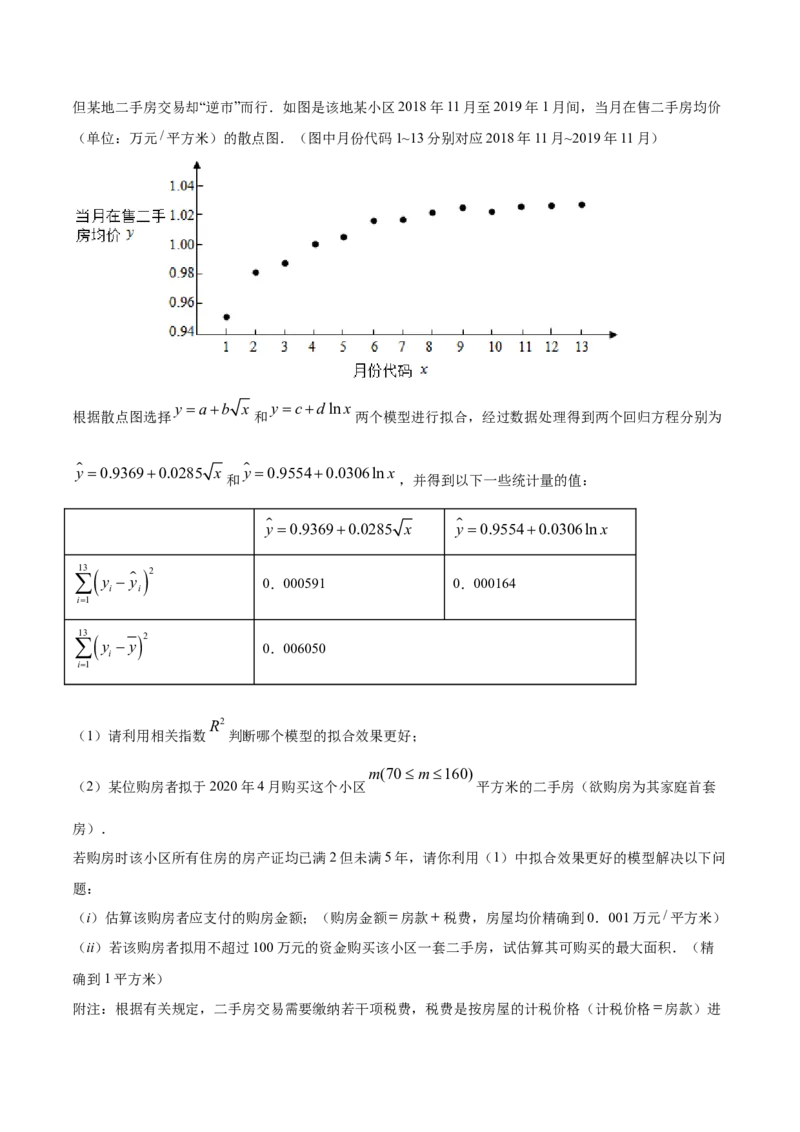v v2 v2 nv2 i i aˆ u b ˆ v e2.7183 i1 i1 22．（2020·梅河口市第五中学其他（理））2019年的“金九银十”变成“铜九铁十”，国各地房价“跳水”严重，但某地二手房交易却“逆市”而行．如图是该地某小区2018年11月至2019年1月间，当月在售二手房均价 （单位：万元/平方米）的散点图．（图中月份代码1~13分别对应2018年11月~2019年11月） y ab x y cdlnx 根据散点图选择 和 两个模型进行拟合，经过数据处理得到两个回归方程分别为 y 0.93690.0285 x y 0.95540.0306lnx 和 ，并得到以下一些统计量的值： y 0.93690.0285 x y 0.95540.0306lnx 13  2  y  y 0．000591 0．000164 i i i1  13  y  y 2 0．006050 i i1 R2 （1）请利用相关指数 判断哪个模型的拟合效果更好； m(70m160) （2）某位购房者拟于2020年4月购买这个小区 平方米的二手房（欲购房为其家庭首套 房）． 若购房时该小区所有住房的房产证均已满2但未满5年，请你利用（1）中拟合效果更好的模型解决以下问 题： （i）估算该购房者应支付的购房金额；（购房金额房款税费，房屋均价精确到0．001万元/平方米） （ii）若该购房者拟用不超过100万元的资金购买该小区一套二手房，试估算其可购买的最大面积．（精 确到1平方米） 附注：根据有关规定，二手房交易需要缴纳若干项税费，税费是按房屋的计税价格（计税价格房款）进行征收的． 1% 房产证满2年但未满5年的征收方式如下：首套面积90平方米以内（含90平方米）为 ；首套面积90 1.5% 3% 平方米以上且140平方米以内（含140平方米） ；首套面积140平方米以上或非首套为 ． ln20.69 ln31.10 ln172.83 ln192.94 2 1.41 3 1.73 参考数据： ， ， ， ， ， ， 17 4.12 19 4.36 ， ． n  2  y  y i i R2 1 i1 参考公式：相关指数  n  y  y 2 ． i i1