南宁二中2024年秋季期中高一数学答案_2024-2025高一（7-7月题库）_2024年11月试卷_1111广西南宁二中2024-2025学年高一秋季期中考试

南宁二中 2024-2025 学年度上学期高一期中考试参考答案
数学
一、选择题：本题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中，只有一个选项是
正确的．请把正确的选项填涂在答题卡相应的位置上．
1.【答案】C
【详解】 集合 ， ， ．
2.【答案】 ∵ C  ={  |  >1}  ={  |−1<  ≤3} ∴  ∩  ={  |1<  ≤ 3}
【详解】 当 时不成立；
B.取

，
.  ⩽0
， ， ，满足 ， ，
， ，不满足 ，因此不正确；
=3  =2  =4  =1  >   > 
C. −  =−，1则  −  =，1对 两  边−同  时>乘  −，  则 ，正确；
1 1 1 1
>0   >0  >     < 
D.取 ， ， ， ，满足条件 ， ，但是 不成立．

3.【  答=案2】B  =−3  =3  =−3  >   >   > 
【详解】根据题意，依次分析选项：
对于 ， ， ，不是偶函数，不符合题意；
2 2 2
对于  ，  (  )=  + ， 2 定  义域  ( 为 −  R) ， =  −2  ≠  +2  =  (  ) ，是偶函数，符合题意；
对于  ，.  (  )=|  | ，  (−  )= |−  |=|  |=，  (是  )奇函数，不符合题意；
−  − 
2 2 2
(  )=  +1  (−  )=(−  ) +1=  +1=−  (  )
对于 ， ，定义域为 ∞ ∞ ，是非奇非偶函数，不符合题意；
−1
4.【答  案  】(  A)=  +1 (− ,−1)∪(−1,+ )
【详解】根据题意， ，且 得
1
5.【答案】D −3<  +1< 4 3  −1>0.  ∈ (3,3).
【详解】对于 ，由图象可知当速度大于 时，乙车的燃油效率大于 ，
当速度大于

时，消耗 升汽油，
40
乙

车
/
的
ℎ
行驶距离大于 ，故A5 错

误
/
；

对于 ，由图象可知当速度相同时，甲车的燃油效率最高，
∴ 40   /ℎ 1 5  
即当速度相同时，消耗 升汽油，甲车的行驶路程最远，

以相同速度行驶相同路
1
程，三辆车中，甲车消耗汽油最少，故B错误；
对于 ，当速度为 时，甲车的燃油效率为 ，即甲车行驶 时，耗油 升，
∴
故甲车  行驶 小时 8 ， 0  路  程 /ℎ 为 ，耗油为 升， 1 故 0  C  错 /  误； 10   1
对于 ，当速
1
度小于 时
80
，

丙车燃油效率
8
大于乙车的燃油效率， 用丙车比用乙车更省油，故D正确.
6.【答

案】C
40   /ℎ ∴
第 页，共 页
学科网（北京）股份有限公司 1 6【详解】令 ， ； ；
1 2
+1 1  −1 +1 2
=  (  ≠1) ∴  =  −1 ∴   = 1 2 +  −1=  −  +1
．  −1
2
∴7.  【 (  答 ) 案 = 】  A−  +1(  ≠1)
【详解】由于 的解集为 ，
2
+   +  >0 −1,3
故 为方程 的两个根，且 则 可得 且

2 −1+3=−   =−2 
−1,3   +   +  =0  <0,  , ,  <0,
(−1)×3=   =−3 
，
1 1 1 1
∴  −  +  =  +  =−(−  −  )⩽−2 −  · −  =−2
当且仅当 即 时等号成立．所以 的最大值为 ．
1 1
8.【答案】−  B=−  ,  =−1  −  +  −2
【详解】 对任意的实数都有 ，
，即 ，
∵  (  +  )=  (  )+  (  )−1
， ，函数 是 上的单调函数，
∴  (2+2)=  (2)+  (2)−1=5  (2)=3
∵函  (数2)=3是  上(4的)=单5调增函数  (，  )  ，即 ，解得 ，
1
∴  (  )  ∴  (1−2  )<3=  (2) 1−2  <2  >−2
即不等式 的解集为 ．
1
二、选择  题 (1 ： − 本 2 题  共 )< 3 3 小题，每小 − 题26 ,+ 分 ∞ ，共 18 分. 在每小题给出的选项中，有多项符合题目要求. 全
部选对得 6 分，部分选对的得部分分，选对但不全的得部分分，有选错的得0分．
9.【答案】ABD
【详解】 因为不等式组 的解集为非空集，得出选项A正确；
−1⩾0
B.由函数的  .定义，在定义域
−
内
+
的
2
每
⩾
一
0
个 ，有且只有一个 与之对应，故选项B正确；
C. ，故 ，   ．故选项C错误；
2
+4,  ⩽0
D.  若(  两)个=函数有相同的定义域  与(0对)应=关4 系  ，[  则(0这)]两=个  (函4)数=是4同−一4=个0函数，故选项D正确．
−4,  >0
10.【答案】BCD
【详解】设正实数 、 满足 ．
，  当且  仅当  +  =1时，等号成立， 的最大值为 ， 选项错误；
+  2 1 1 1
≤( 2 ) =4  =  =2   4 
，则 ，
2
∵  +  =  +  +2   ≤2  +  =2  +  ≤ 2
当且仅当 时，等号成立， 选项正确；
2
=  = 2 
1 1 1 1 1
+ = 3  +3  +
+2  2  +  3  +2  2  + 
1 1 1 1 2  +   +2 
= [(  +2  )+(2  +  )]( + )=第 页(2，+共 页 + )
3  +2  2  +  3  +2  2  + 
学科网（北京）股份有限公司 2 6，当且仅当 时，等号成立， 选项正确；
1  +2  2  +  4 1
≥3 2+2 2  +  ⋅  +2  =3  =  =2 
，
2 2
2 2 2 2  +   +  1
+  =  +  −2   ≥  +  −2× 2 = 2 =2
当且仅当 时，等号成立， 选项正确．
1
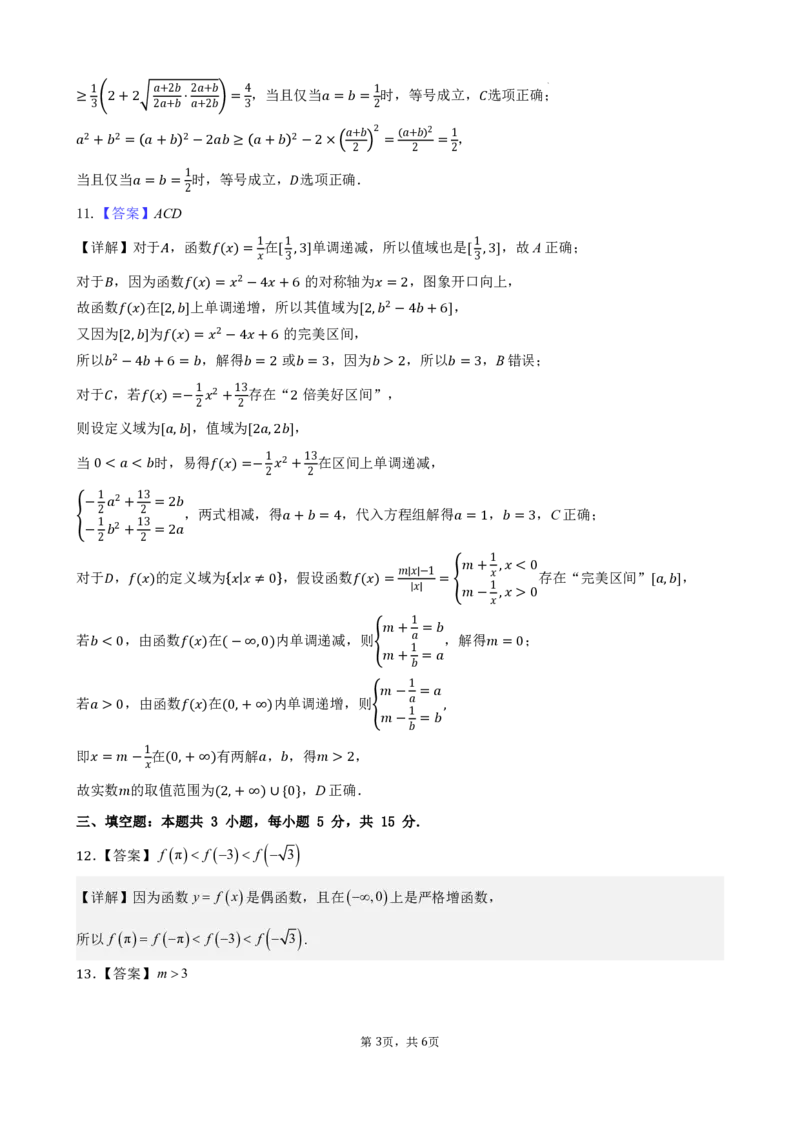
11.【答案  】=A  C=D2 
【详解】对于 ，函数 在 单调递减，所以值域也是 ，故A正确；
1 1 1
对于 ，因为函  数  (  )=  [3,3的] 对称轴为 ，图象开口[3向,3上] ，
2
故函数 在 上单调递增，所以其值域为 ，
(  )=  −4  +6  =2
2
又因为 为 的完美区间，
(  ) [2,  ] [2,  −4  +6]
2
所以
[2,  ]  (  )=
，

解
−
得
4  +6
或 ，因为 ，所以 ，B错误；
2
对于  ，−若4  +6=   存=在2“  倍=美3好区间  ”>，2  =3
1 2 13
则设定  义域  为(  )=−，2  值域+为2 2，
当 时[  ，,  易] 得 [2  ,2  ] 在区间上单调递减，
1 2 13
0<  <   (  )=−2  + 2
，两式相减，得 ，代入方程组解得 ， ，C正确；
1 2 13
−2  + 2 =2 
1 2 13  +  =4  =1  =3
−2  + 2 =2 
对于 ， 的定义域为 ，假设函数 存在“完美区间” ，
1
−1  +  ,  <0
(  )   ≠0  (  )=  = 1 [  ,  ]
−  ,  >0
若 ，由函数 在 内单调递减，则 ，解得 ；
1
+  = 
<0  (  ) (−∞,0) 1  =0
+  = 
若 ，由函数 在 内单调递增，则
1
−  = 
>0  (  ) (0,+∞) 1 ,
即 在 有两解 ， ，得 ，  −  = 
1
故实  =数  的−取  值(0范,+围∞为)   ，D  正>确2．
三、填  空题：本题共 3(2小,+题∞，)每∪小{0}题 5 分，共 15 分.
．【答案】 f π f 3 f   3 
12
【详解】因为函数y f x是偶函数，且在,0上是严格增函数，
所以 f π f π f 3 f   3 
．【答案】m3 .
13
第 页，共 页
学科网（北京）股份有限公司 3 621m
【详解】根据题意可知，若q的充分不必要条件是p需满足 ，解得m3；
2m1
但且两端等号不同时成立，所以m 3，即m3；因此实数m的取值范围为m3
32 5
．【答案】 3 .
4
14
 x3 3,x,13,
【详解】当x23x3 x33时，解得x1或x3，所以 f x ，
x23x3,x1,3
作出 f x的图象如下图所示：
由图象可知：当x3时， f x有最大值，所以 f x  f 33；
max
当 f x 3 时，解得x 3 或 3 或 21 ；
4 4 2 4
当 f x2时，x 3 5 或x4，
2
由图象可知：当m   3 , 3  ，n 3 5 时，f x的值域为   3 ,2   ，此时nm的最大值为 3 5  3  32 5 ；
4 2 2 4  2 4 4
当m4,n 21 时， f x的值域为   3 ,2   ，此时nm 5  32 5 ，
4 4  4 4
32 5
由上可知，nm的最大值为 ．
4
四、解答题：本题共5小题，共77分，解答应写出必要的文字说明、证明过程或演算步骤．
15.【详解】（ ）因为x0，y0，x y2，
4 1 114 1  1 4 y x  1   9
所以     (x y) 4  1 5 2 4  ，
x y 2x y  2 x y  2 2
4y x 4 2 4 1 9
当且仅当  ，即x ,y 时等号成立，故  的最小值为 ；
x y 3 3 x y 2
1
（ ）因为0 x ，所以02x1,012x1，
2
2
2x(12x) 12x12x 2 1
所以x(12x)     ，
2 2 2  8
第 页，共 页
学科网（北京）股份有限公司 4 61 1
当且仅当2x12x，即x 时等号成立，故x(12x)的最大值为
4 8
16.【详解】（ ）若 p为真命题，则AB， .
所以2a6，所以a3
1
（ ）当q为假命题时，.即“xR ,x22xa0”为真命题，
2
所以44a0，所以a的取值范围为  a a1  ，
由（ ）知命题 p为假命题时，a的取值范围为  a a3 
1 .
所以当 p,q均为假命题时a的取值范围为  a a3  a a1  a 1a3  ，
所以当命题 p和命题q至少有一个为真命题时a的取值范围为  a a1或a3
17.【详解】（ ）由题意，得wt f tgt100  1 1   125 t25  .
 t
1
  100 

100t 101 ，1t＜25，tN 
  t 

 100  149 150 t   ，25t30，tN 
   t 
100 100 100
（ ）①当1t25时，因为t  2 t  20，当且仅当t  ，
t t t
即2t10时取等号
所以当t＝ 时，w(t)有最小值 ；
.
当t＝ 时，
10
w(t)有最大值
1
；
2100
150
②当215t30时，∵ 2t0在200 ， 上递减，
t
∴当t＝ 时，w(t)有最小值 [25 30]
当 时，w(t)有最大值
30 12400;
∵ ＜ ， ，
t=25 13000.
∴
1
当 21t＝
00 1
时
24
，
0
该
0
商
1
品
30
的
00
日
<
销
20
售
20
金
0
额w(t)取得最小值为 ；
当t 时，该商品的日销售金额w(t)取得最大值为 ．
10 12100
18.【=1详解】（ ）因为3A，所以当x3时，ax22(a02030)x30
将x3代入得19a3(a3)30，即9a3a930，解得a1.
（ ）由ax2(a3)x30 ，因式分解得(ax3)(x1)0， .
当2a0时，开口向上，不等式的解 含有无数个整数，不符合题意，舍去；
当a=0时，不等式的解为x1，含有无数个整数，不符合题意，舍去；
A
3 3
当a0时， 1，不等式的解为 x1
a a
.
第 页，共 页
学科网（北京）股份有限公司 5 63
因为集合A中有且仅有两个整数，这两个整数只能是1，0 所以2 1，
a
3 3 .
当2 时，2a3，解得a ；
a 2
3
当 1时，3a，解得a3
a
3 .
所以a
2
.
19.【详解】（ ）根据题意，函数 f x是定义域在2,2上的奇函数，
1 b
则 f 00，即有 f 0 ，解可得b0，
4
ax
则 f x ，
4x2
ax
ax
则 f x  f x  ，则此时 f x为奇函数，
4x2 4x2
设2x x 2，
1 2
ax ax ax x 4xx 
则 f x  f x  1  2  1 2 1 2 ，
1 2 4x2 4x2  4x2 4x2
1 2 1 2
又2x x 2，a0，
1 2
则x x 0，4xx 0，4x2 0，4x2 0，
1 2 1 2 1 2
a  x x  4x x 
则 f  x 1  f  x 2   4 1 x2 2  4x 1 2 2  0，即 f x 1  f x 2 ，
1 2
故 f x在2,2上是增函数
.
（ ）根据题意， f x是定义在2,2上的奇函数，且在2,2上单调递增，
f 2 t2m   f 1t0 f  t2m  f 1t f  t2m   f t1，
则有2t2mt12对t0,1，恒成立，
 m  t22 
 min
则有  m  t22  ，则1m2，
 max
m  t2t1 

max
即m的取值范围为1,2．
第 页，共 页
学科网（北京）股份有限公司 6 6