文档内容
高二年级下学期期末仿真卷 04
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知等差数列{a}的前n项和为S,若a=3,S=54,则a+a =( )
n n 6 9 1 10
A.7 B.8 C.9 D.10
【答案】C
【分析】利用等差数列的通项公式与求和公式即可得出.
【解答】解:设等差数列{a}的公差为d,∵a=3,S=54,
n 6 9
∴a+5d=3,9a+36d=54,
1 1
解得a=18,d=﹣3.
1
则a+a =2×18﹣9×3=9.
1 10
故选:C.
【知识点】等差数列的性质
2.设复数 是虚数单位),则 =( )
A.1+i B.﹣i C.i D.0
【答案】D
【分析】先化简1+x,再根据所求式子为 (1+x)2020﹣1,从而求得结果.
【解答】解:复数 是虚数单位),而 =(1+x)
2020﹣1,
而 1+x= = = =i,
故 =(1+x)2020﹣1=i2020﹣1=1﹣1=0,
故选:D.
【知识点】二项式定理
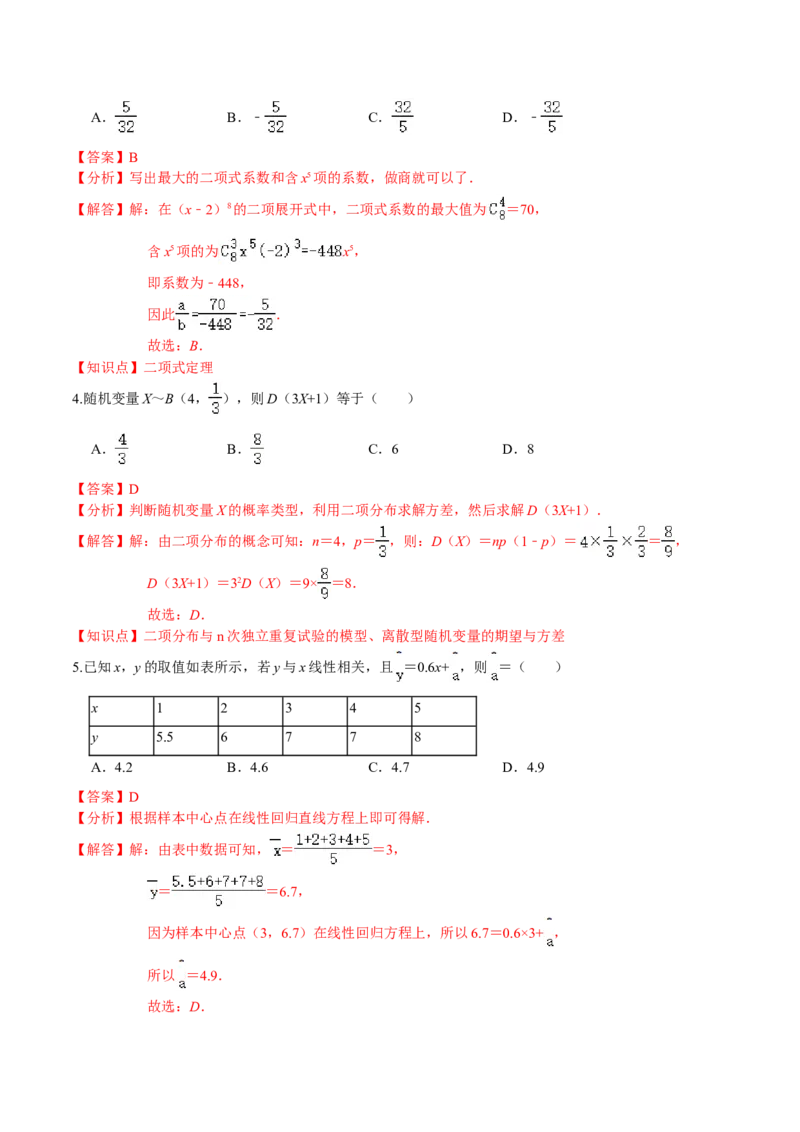
3.在(x﹣2)8的二项展开式中,二项式系数的最大值为a,含x5项的系数为b,则 =( )A. B.﹣ C. D.﹣
【答案】B
【分析】写出最大的二项式系数和含x5项的系数,做商就可以了.
【解答】解:在(x﹣2)8的二项展开式中,二项式系数的最大值为 =70,
含x5项的为 x5,
即系数为﹣448,
因此 .
故选:B.
【知识点】二项式定理
4.随机变量X~B(4, ),则D(3X+1)等于( )
A. B. C.6 D.8
【答案】D
【分析】判断随机变量X的概率类型,利用二项分布求解方差,然后求解D(3X+1).
【解答】解:由二项分布的概念可知:n=4,p= ,则:D(X)=np(1﹣p)= = ,
D(3X+1)=32D(X)=9× =8.
故选:D.
【知识点】二项分布与n次独立重复试验的模型、离散型随机变量的期望与方差
5.已知x,y的取值如表所示,若y与x线性相关,且 =0.6x+ ,则 =( )
x 1 2 3 4 5
y 5.5 6 7 7 8
A.4.2 B.4.6 C.4.7 D.4.9
【答案】D
【分析】根据样本中心点在线性回归直线方程上即可得解.
【解答】解:由表中数据可知, = =3,
= =6.7,
因为样本中心点(3,6.7)在线性回归方程上,所以6.7=0.6×3+ ,
所以 =4.9.
故选:D.【知识点】线性回归方程
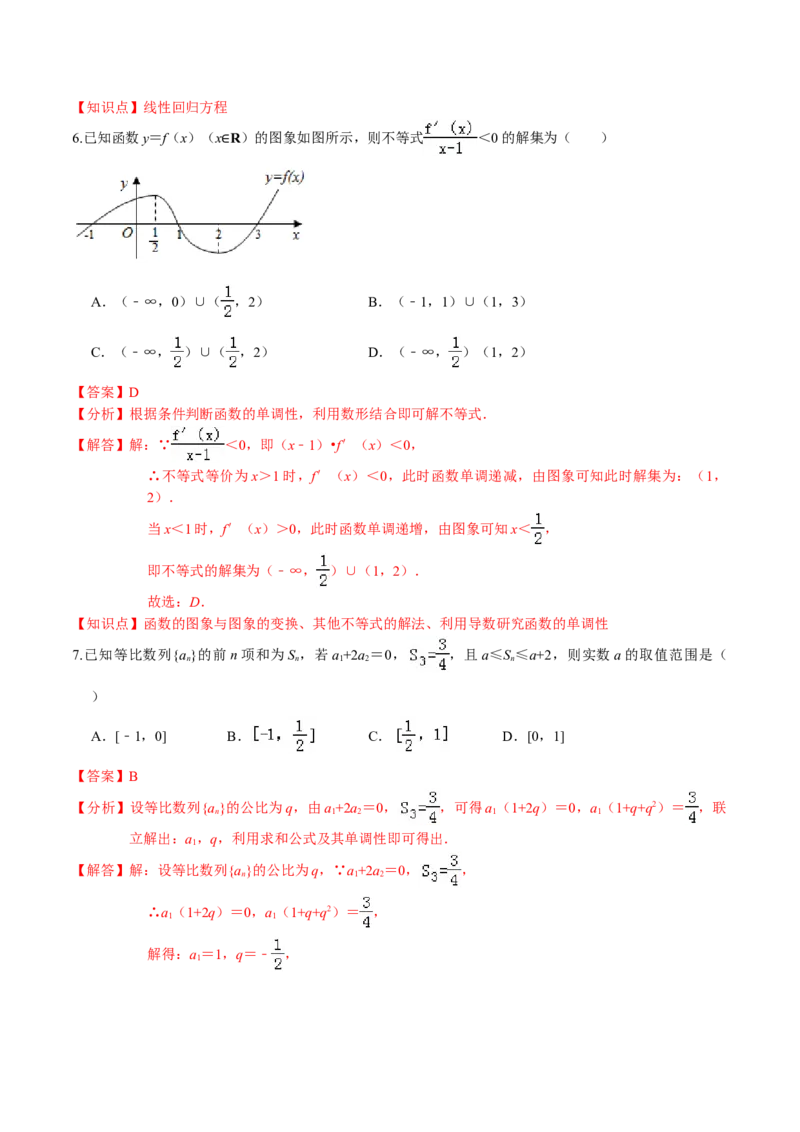
6.已知函数y=f(x)(x R)的图象如图所示,则不等式 <0的解集为( )
∈
A.(﹣∞,0)∪( ,2) B.(﹣1,1)∪(1,3)
C.(﹣∞, )∪( ,2) D.(﹣∞, )(1,2)
【答案】D
【分析】根据条件判断函数的单调性,利用数形结合即可解不等式.
【解答】解:∵ <0,即(x﹣1)•f′(x)<0,
∴不等式等价为x>1时,f′(x)<0,此时函数单调递减,由图象可知此时解集为:(1,
2).
当x<1时,f′(x)>0,此时函数单调递增,由图象可知x< ,
即不等式的解集为(﹣∞, )∪(1,2).
故选:D.
【知识点】函数的图象与图象的变换、其他不等式的解法、利用导数研究函数的单调性
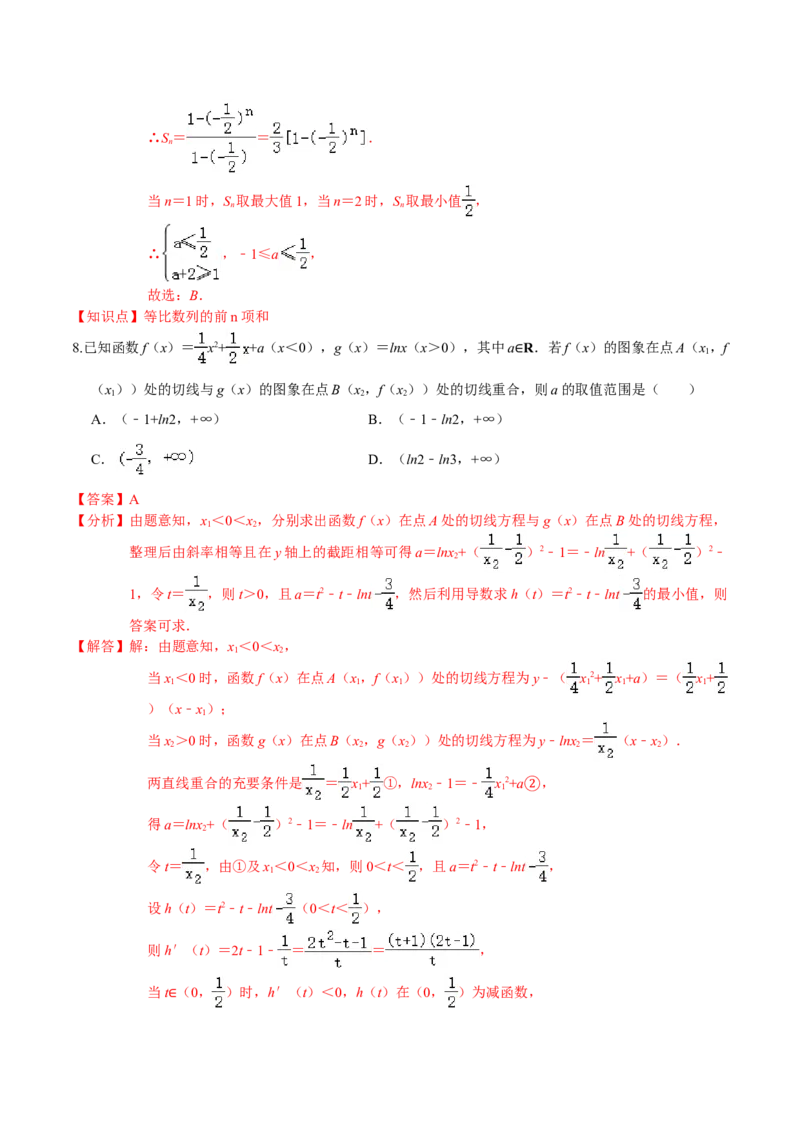
7.已知等比数列{a}的前n项和为S ,若a+2a =0, ,且a≤S≤a+2,则实数a的取值范围是(
n n 1 2 n
)
A.[﹣1,0] B. C. D.[0,1]
【答案】B
【分析】设等比数列{a}的公比为q,由a+2a =0, ,可得a (1+2q)=0,a (1+q+q2)= ,联
n 1 2 1 1
立解出:a,q,利用求和公式及其单调性即可得出.
1
【解答】解:设等比数列{a}的公比为q,∵a+2a=0, ,
n 1 2
∴a(1+2q)=0,a(1+q+q2)= ,
1 1
解得:a=1,q=﹣ ,
1∴S= = .
n
当n=1时,S 取最大值1,当n=2时,S 取最小值 ,
n n
∴ ,﹣1≤a ,
故选:B.
【知识点】等比数列的前n项和
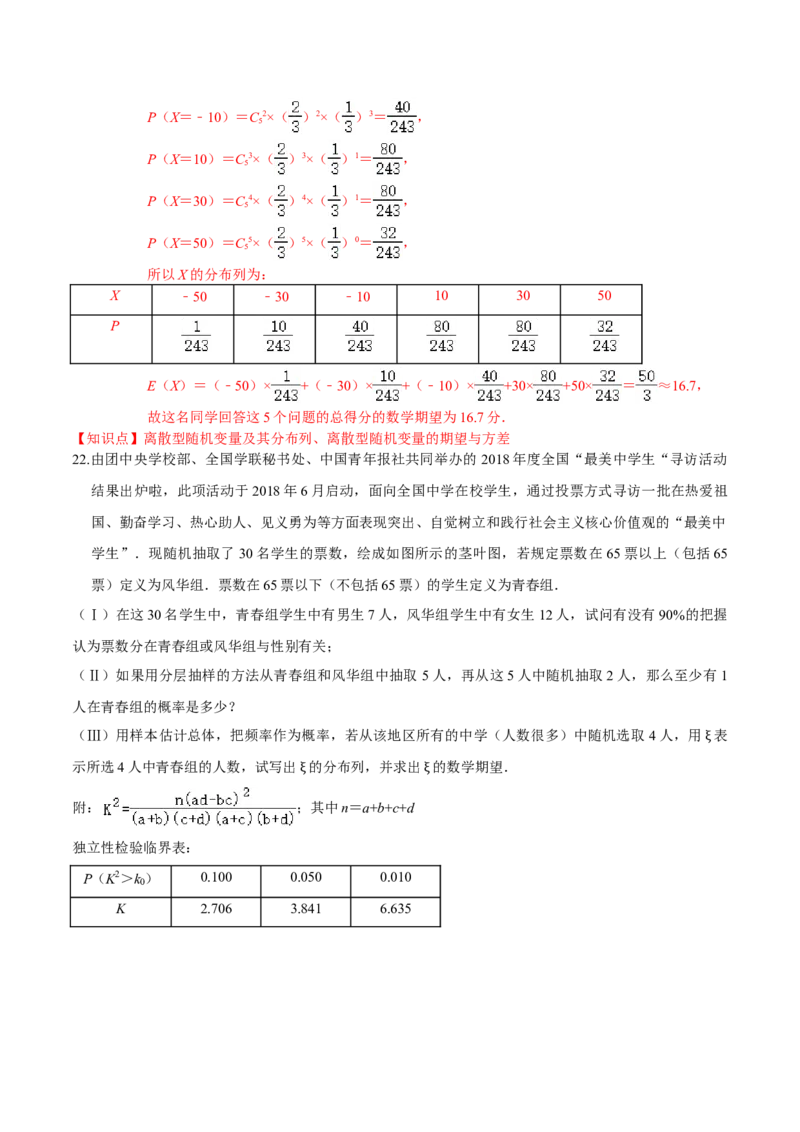
8.已知函数f(x)= x2+ +a(x<0),g(x)=lnx(x>0),其中a R.若f(x)的图象在点A(x,f
1
∈
(x))处的切线与g(x)的图象在点B(x,f(x))处的切线重合,则a的取值范围是( )
1 2 2
A.(﹣1+ln2,+∞) B.(﹣1﹣ln2,+∞)
C. D.(ln2﹣ln3,+∞)
【答案】A
【分析】由题意知,x <0<x ,分别求出函数f(x)在点A处的切线方程与g(x)在点B处的切线方程,
1 2
整理后由斜率相等且在y轴上的截距相等可得a=lnx +( )2﹣1=﹣ln +( )2﹣
2
1,令t= ,则t>0,且a=t2﹣t﹣lnt ,然后利用导数求h(t)=t2﹣t﹣lnt 的最小值,则
答案可求.
【解答】解:由题意知,x<0<x,
1 2
当x<0时,函数f(x)在点A(x,f(x))处的切线方程为y﹣( x2+ x+a)=( x+
1 1 1 1 1 1
)(x﹣x);
1
当x>0时,函数g(x)在点B(x,g(x))处的切线方程为y﹣lnx = (x﹣x).
2 2 2 2 2
两直线重合的充要条件是 = x+ ①,lnx ﹣1=﹣ x2+a ,
1 2 1
②
得a=lnx +( )2﹣1=﹣ln +( )2﹣1,
2
令t= ,由①及x<0<x 知,则0<t< ,且a=t2﹣t﹣lnt ,
1 2
设h(t)=t2﹣t﹣lnt (0<t< ),
则h′(t)=2t﹣1﹣ = = ,
当t (0, )时,h′(t)<0,h(t)在(0, )为减函数,
∈则h(t)>h( )=ln2﹣1,又t→0时,h(t)→+∞.
∴a>ln2﹣1,
则a的取值范围是(ln2﹣1,+∞).
故选:A.
【知识点】利用导数研究曲线上某点切线方程
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。
9.已知数列{a}是等差数列,前n项和为S,满足a+5a=S,下列选项正确的有( )
n n 1 3 8
A.a =0 B.S 最小 C.S=S D.S =0
10 10 7 12 20
【答案】AC
【分析】根据题意,结合等差数列的前n项和公式以及通项公式,依次分析选项,综合即可得答案.
【解答】解:根据题意,数列{a}是等差数列,若a+5a =S ,即a+5a+10d=8a+28d,变形可得a =﹣
n 1 3 8 1 1 1 1
9d,
又由a=a+(n﹣1)d=(n﹣10)d,则有a =0,故A一定正确,
n 1 10
不能确定a 和d的符号,不能确定S 最小,故B不正确;
1 10
又由S=na+ =﹣9nd+ = ×(n2﹣19n),则有S=S ,故C一定正确,
n 1 7 12
则S =20a+ d=﹣180d+190d=﹣10d,S ≠0,则D不正确,
20 1 20
故选:AC.
【知识点】等差数列的前n项和
10.现有3个男生4个女生,若从中选取3个学生,则( )
A.选取的3个学生都是女生的不同选法共有4种
B.选取的3个学生恰有1个女生的不同选法共有24种
C.选取的3个学生至少有1个女生的不同选法共有34种
D.选取的3个学生至多有1个男生的不同选法共有18种
【答案】AC
【分析】根据组合的定义和分步计数原理即可求出.
【解答】解:选取的3个学生都是女生的不同的选法共有C 3=4,故A正确;
4
恰有1个女生的不同选法共有C 2C 1=12种,故B错误;
3 4
至少有1个女生的不同选法共有C 3﹣C 3=34种,故C正确;
7 3
选取的3个学生至多有1个男生的不同选法共C 1C 2+C 3=22种,故D错误.
3 4 4
故选:AC.
【知识点】排列、组合及简单计数问题
11.设离散型随机变量X的分布列为
X 0 1 2 3 4
P q 0.4 0.1 0.2 0.2若离散型随机变量Y满足Y=2X+1,则下列结果正确的有( )
A.q=0.1 B.EX=2,DX=1.4
C.EX=2,DX=1.8 D.EY=5,DY=7.2
【答案】CD
【分析】由离散型随机变量X的分布列的性质求出p=0.1,由此能求出E(X),D(X),再由离散型随
机变量Y满足Y=2X+1,能求出E(Y)和D(Y).
【解答】解:由离散型随机变量X的分布列的性质得:
p=1﹣0.4﹣0.1﹣0.2﹣0.2=0.1,
E(X)=0×0.1+1×0.4+2×0.1+3×0.2+4×0.2=2,
D(X)=(0﹣2)2×0.1+(1﹣2)2×0.4+(2﹣2)2×0.1+(3﹣2)2×0.2+(4﹣2)2×0.2=1.8,
∵离散型随机变量Y满足Y=2X+1,
∴E(Y)=2E(X)+1=5,
D(Y)=4D(X)=7.2.
故选:CD.
【知识点】离散型随机变量及其分布列
12.已知函数f(x)=xlnx,若0<x<x,则下列选项正确的是( )
1 2
A.
B.x+f(x)<x+f(x)
1 1 2 2
C.xf(x)<xf(x)
2 1 1 2
D.当lnx>﹣1时,xf(x)+xf(x)>xf(x)+xf(x)
1 1 2 2 2 1 1 2
【答案】CD
【分析】根据条件分别构造不同的函数,求函数的导数,利用函数单调性和导数之间的关系进行判断即可.
【解答】解:f′(x)=lnx+1,
x (0, )时,f′(x)<0,∴f(x)在(0, )上单调递减,
∈
x ( ,+∞),f′(x)>0,.∴f(x)在( ,+∞)上单调递增.
对∈于A,令g(x)=f(x)﹣x=xlnx﹣x,
则g′(x)=lnx,设x,x (1,+∞),
1 2
则g′(x)>0,∴函数g(x)在(1,+∞)上是增函数,
∈
∴由x>x 得g(x)>g(x);
2 1 2 1
∴f(x)﹣x>f(x)﹣x,∴ >1,故A错误;
2 2 1 1
对于B,令g(x)=f(x)+x=xlnx+x,
∴g′(x)=lnx+2,
∴x (e﹣2,+∞)时,g′(x)>0,g(x)单调递增,
x (0,e﹣2)时,g′(x)<0,g(x)单调递减.
∈
∴x+f(x)与x+f(x)无法比较大小.
1 1 2 2
∈故B错误;
对于C,令g(x)= =lnx,则g′(x)= ,(0,+∞)上函数单调递增,
∵x>x>0,∴g(x)>g(x),∴x•f(x)<x•f(x),即C正确;
2 1 2 1 2 1 1 2
对于D,∵lnx>﹣1时,f′(x)=lnx+1>,∴f(x)单调递增,
∴x•f(x )+x•f(x )﹣[xf(x )+xf(x )]=x[f(x )﹣f(x )]+x[f(x )﹣f(x )]=(x
1 1 2 2 2 1 1 2 1 1 2 2 2 1 1
﹣x)[f(x)﹣f(x)]>0,故D正确.
2 1 2
故选:CD.
【知识点】利用导数研究函数的单调性
三、填空题:本题共4小题,每小题5分,共20分。
13.已知等差数列{a}的前n项和为S,若S=6,S=﹣8,则S= ﹣ .
n n 3 6 9
【答案】-36
【分析】利用等差数列的前n项和的性质即可得出.
【解答】解:由题意可得:2×(﹣8﹣6)=6+S﹣(﹣8),解得S=﹣36.
9 9
故答案为:﹣36.
【知识点】等差数列的性质
14.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前
期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜
的概率为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是 .
【答案】0.18
【分析】甲队以4:1获胜包含的情况有:①前5场比赛中,第一场负,另外4场全胜,②前5场比赛中,
第二场负,另外4场全胜,③前5场比赛中,第三场负,另外4场全胜,④前5场比赛中,第四
场负,另外4场全胜,由此能求出甲队以4:1获胜的概率.
【解答】解:甲队的主客场安排依次为“主主客客主客主”.
设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,
甲队以4:1获胜包含的情况有:
①前5场比赛中,第一场负,另外4场全胜,其概率为:p=0.4×0.6×0.5×0.5×0.6=0.036,
1
②前5场比赛中,第二场负,另外4场全胜,其概率为:p=0.6×0.4×0.5×0.5×0.6=0.036,
2
③前5场比赛中,第三场负,另外4场全胜,其概率为:p=0.6×0.6×0.5×0.5×0.6=0.054,
3
④前5场比赛中,第四场负,另外4场全胜,其概率为:p=0.6×0.6×0.5×0.5×0.6=0.054,
3
则甲队以4:1获胜的概率为:
p=p+p+p+p=0.036+0.036+0.054+0.054=0.18.
1 2 3 4
故答案为:0.18.
【知识点】相互独立事件和相互独立事件的概率乘法公式
15.已知(x﹣ )(1﹣x)4的展开式中x2的系数为4,则a= ,(x﹣ )(1﹣x)4的展开式中的常数
项为 .
【答案】【第1空】2
【第2空】8【分析】把(1﹣x)4按照二项式定理展开,可得(x﹣ )(1﹣x)4的展开式中x2的系数和常数项.
【解答】解:∵(x﹣ )(1﹣x)4=(x﹣ )( ﹣ •x+ •x2﹣ •x3+ •x4),
故展开式中x2的系数为﹣4+a× =4,则a=2.
常数项为﹣a×(﹣ )=4a=8,
故答案为:2;8.
【知识点】二项式定理
16.已知函数 ,当x [0,1]时,函数f(x)仅在x=1处取得最大值,则a
∈
的取值范围是 .
【分析】求出原函数的导函数,对a分类,根据函数在[0,1]上的单调性逐一分析求解.
【解答】解:f′(x)=2ax2+(2a﹣1)x.
若a=0,则f′(x)≤0在[0,1]上恒成立,f(x)在[0,1]上单调递减,不合题意;
若a<0,由f′(x)=0,得 <0,x=0,
2
f(x)在[0,1]上单调递减,不合题意;
若a>0,当a 时, ,f(x)在[0,1]上单调递增,符合题意;
当0<a≤ 时, ,f(x)在[0,1]上单调递减,不合题意;
当 <a< 时,0< <1,
f(x)在[0, )上单调递减,在( ,1]上单调递增,
要使当x [0,1]时,函数f(x)仅在x=1处取得最大值,
则f(1)∈= ,即a .
综上,实数a的取值范围为( ,+∞).
故答案为:( ).
【知识点】利用导数研究函数的最值
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.在 (n≥3,n N*)的展开式中,第2,3,4项的二项式系数依次成等差数列.
∈
(1)求n的值;(2)求展开式中含x2的项.
【分析】(1)由题意可得 2 = + ,由此求得n的值.
(2)先求出二项式展开式的通项公式,再令x的幂指数等于2,求得r的值,即可求得展开式
中的含x2的项.
【解答】解:(1)∵在 (n≥3,n N*)的展开式中,第2,3,4项的二项式系数依次成等
∈
差数列,
即 2 = + ,求得n=7,或n=2(舍去).
(2)展开式的通项公式为 T = • • ,令 =2,求得r=2,
r+1
可得展开式中含x2的项为T= • •x2= •x2.
3
【知识点】二项式定理、等差数列的通项公式
18.已知函数f(x)=aex﹣1﹣lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
【分析】(1)根据导数的几何意义即可求出切线方程,可得三角形的面积;
(2)方法一:不等式等价于ex﹣1+lna+lna+x﹣1≥lnx+x=elnx+lnx,令g(t)=et+t,根据函数单
调性可得lna>lnx﹣x+1,再构造函数h(x)=lnx﹣x+1,利用导数求出函数的最值,即可求出
a的范围;
方法二:构造两个基本不等式ex>x﹣1,x﹣1≥lnx,则原不等式转化为x(a﹣1)≥﹣lna,再
分类讨论即可求出a的取值范围,
方法三:利用分类讨论的思想,当0<a<1,此时不符合题意,当a≥1时,f(x)≥ex﹣1﹣
lnx,令g(x)=ex﹣1﹣lnx,
再根据导数和函数最值的关系即可证明,
方法四:先根据导数和函数的最值的关系求出f(x)≥f(x )= ﹣2lnx +1﹣x≥1,lna=1
0 0 0
﹣x﹣lnx ,再求出x 的范围,再利用导数求1﹣x﹣lnx 的范围,即可求出a的范围.
0 0 0 0 0
方法五:f(x)≥1等价于aex﹣1﹣lnx+lna≥1,构造函数hg(a)=a+lna﹣1,利用导数求出
函数的最值,即可求出a的范围.
【解答】解:(1)当a=e时,f(x)=ex﹣lnx+1,
∴f′(x)=ex﹣ ,
∴f′(1)=e﹣1,
∵f(1)=e+1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y﹣(e+1)=(e﹣1)(x﹣1),
当x=0时,y=2,当y=0时,x= ,
∴曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积S= ×2× =.
(2)方法一:由f(x)≥1,可得aex﹣1﹣lnx+lna≥1,即ex﹣1+lna﹣lnx+lna≥1,
即ex﹣1+lna+lna+x﹣1≥lnx+x=elnx+lnx,
令g(t)=et+t,
则g′(t)=et+1>0,
∴g(t)在R上单调递增,
∵g(lna+x﹣1)≥g(lnx)
∴lna+x﹣1≥lnx,
即lna≥lnx﹣x+1,
令h(x)=lnx﹣x+1,
∴h′(x)= ﹣1= ,
当0<x<1时,h′(x)>0,函数h(x)单调递增,
当x>1时,h′(x)<0,函数h(x)单调递减,
∴h(x)≤h(1)=0,
∴lna≥0,
∴a≥1,
故a的范围为[1,+∞).
方法二:由f(x)≥1可得aex﹣1﹣lnx+lna≥1,x>0,a>0,
即aex﹣1﹣1≥lnx﹣lna,
设g(x)=ex﹣x﹣1,
∴g′(x)=ex﹣1>0恒成立,
∴g(x)在(0,+∞)单调递增,
∴g(x)>g(0)=1﹣0﹣1=0,
∴ex﹣x﹣1>0,
即ex>x+1,
再设h(x)=x﹣1﹣lnx,
∴h′(x)=1﹣ = ,
当0<x<1时,h′(x)<0,函数h(x)单调递减,
当x>1时,h′(x)>0,函数h(x)单调递增,
∴h(x)≥h(1)=0,
∴x﹣1﹣lnx≥0,
即x﹣1≥lnx
∴ex﹣1≥x,则aex﹣1≥ax,
此时只需要证ax≥x﹣lna,
即证x(a﹣1)≥﹣lna,
当a≥1时,
∴x(a﹣1)>0>﹣lna恒成立,
当0<a<1时,x(a﹣1)<0<﹣lna,此时x(a﹣1)≥﹣lna不成立,
综上所述a的取值范围为[1,+∞).
方法三:由题意可得x (0,+∞),a (0,+∞),
∈ ∈∴f′(x)=aex﹣1﹣ ,
易知f′(x)在(0,+∞)上为增函数,
①当0<a<1时,f′(1)=a﹣1<0,f′( )=a ﹣a=a( ﹣1)>0,
∴存在x (1, )使得f′(x)=0,
0 0
当x (1,∈x)时,f′(x)<0,函数f(x)单调递减,
0
∴f(x)<f(1)=a+lna<a<1,不满足题意,
∈
②当a≥1时,ex﹣1>0,lna>0,
∴f(x)≥ex﹣1﹣lnx,
令g(x)=ex﹣1﹣lnx,
∴g′(x)=ex﹣1﹣ ,
易知g′(x)在(0,+∞)上为增函数,
∵g′(1)=0,
∴当x (0,1)时,g′(x)<0,函数g(x)单调递减,
当x (1,+∞)时,g′(x)>0,函数g(x)单调递增,
∈
∴g(x)≥g(1)=1,
∈
即f(x)≥1,
综上所述a的取值范围为[1,+∞).
方法四:∵f(x)=aex﹣1﹣lnx+lna,x>0,a>0,
∴f′(x)=aex﹣1﹣ ,易知f′(x)在(0,+∞)上为增函数,
∵y=aex﹣1在(0,+∞)上为增函数,y= 在0,+∞)上为减函数,
∴y=aex﹣1与y= 在0,+∞)上有交点,
∴存在x (0,+∞),使得f′(x)=a ﹣ =0,
0 0
∈
则a = ,则lna+x﹣1=﹣lnx ,即lna=1﹣x﹣lnx ,
0 0 0 0
当x (0,x)时,f′(x)<0,函数f(x)单调递减,
0
当x (x,+∞)时,f′(x)>0,函数f(x)单调递增,
0
∈
∴f(∈x)≥f(x)=a ﹣lnx +lna
0 0
= ﹣lnx +1﹣x﹣lnx = ﹣2lnx +1﹣x≥1
0 0 0 0 0
∴ ﹣2lnx ﹣x≥0
0 0
设g(x)= ﹣2lnx﹣x,
易知函数g(x)在(0,+∞)上单调递减,且g(1)=1﹣0﹣1=0,
∴当x (0,1]时,g(x)≥0,
∈∴x (0,1]时, ﹣2lnx ﹣x≥0,
0 0 0
设h(∈ x)=1﹣x﹣lnx,x (0,1],
∴h′(x)=﹣1﹣ <0∈恒成立,
∴h(x)在(0,1]上单调递减,
∴h(x)≥h(1)=1﹣1﹣ln1=0,
当x→0时,h(x)→+∞,
∴lna≥0=ln1,
∴a≥1.
方法五:f(x)≥1等价于aex﹣1﹣lnx+lna≥1,该不等式恒成立.
当x=1时,有a+lna≥1,其中a>0.
设g(a)=a+lna﹣1,则g'(a)=1+ >0,
则g(a)单调增,且g(1)=0.
所以若a+lna≥1成立,则必有a≥1.
∴下面证明当a≥1时,f(x)≥1成立.
∵ex≥x+1,
把x换成x﹣1得到ex﹣1≥x,
∵x﹣1≥lnx,∴x﹣lnx≥1.
∴f(x)=aex﹣1﹣lnx+lna≥ex﹣1﹣lnx≥x﹣lnx≥1.
综上,a≥1.
【知识点】利用导数研究曲线上某点切线方程、利用导数研究函数的单调性
19.已知集合X={2,3,4,6,8,15,17},数列{a}(n N*)是公比为q(q>l)的等比数列,且等比数
n
列的前三项满足a、a、a X. ∈
1 2 3
(1)求通项公式a n ; ∈
(2)若S 是等比数列{a}的前n项和,记A=S+S+S+…+S ,试用等比数列求和公式化简A(用含n的式
n n 1 2 3 n
子表示)
【分析】(1)求得数列的首项和公比均为2,可得所求通项公式;
(2)求得S= =2n+1﹣2,再由数列的分组求和和等比数列的求和公式,化简可得所
n
求和.
【解答】解:(1)集合X={2,3,4,6,8,15,17},数列{a}是公比为q(q>l)的等比数列,
n
且等比数列的前三项满足a、a、a X.可得a=2,a=4,a=8,
1 2 3 1 2 3
即有q=2,通项公式a=2n;
n
∈
(2)S= =2n+1﹣2,
n
A=S+S+S+…+S=(4+8+…+2n+1)﹣2n= ﹣2n=2n+2﹣4﹣2n.
1 2 3 n
【知识点】等比数列的前n项和、等比数列的性质
20.设 是正实数,(1+ x)20的二项展开式为a+ax+ax2+……+a x20,其中a,a,……,a 均为常数
0 1 2 20 0 1 20
(1)λ若a
3
=12a
2
,求 的λ 值;
λ(2)若a≥a 对一切n {0,1,…,20}均成立,求 的取值范围.
5 n
【分析】(1)根据通项∈公式列式可得; λ
(2)假设第r+1项系数最大,依题意得 ,解得 ≤r≤ ,
根据a 最大列式可得.
5
【解答】解:(1)通项公式为T =C r•xr,r=0,1,2,…,20.
r+1
λ
∴由a=12a 得,C 3=12C 2,解得 =2.
3 2
λ λ λ
(2)假设第r+1项系数最大,依题意得 ,解得 ≤r≤ ,
∴ ∴ ,解得 ≤ ≤ .
λ
【知识点】二项式定理
21.某中学组织学生参加《网络安全知识竞赛》,在必答环节中,需回答5个问题,竞赛规则规定:每题回
答正确得10分,回答不正确得﹣10分.假设某同学每题回答正确的概率均为 ,且各题回答正确与否
相互之间没有影响.
(Ⅰ)求这名同学总得分X [﹣10,10]的概率;
(Ⅱ)求这名同学回答这5∈个问题的总得分的分布列和数学期望(结果保留一位小数).
【分析】(Ⅰ)确定X [﹣10,10]的实质是X=﹣10,10,即对2道错3道或对3道错2道,再利用概率
公式即可求解;
∈
(Ⅱ)先列出总得分的所有可能取值,并求出相对应的概率,再写出分布列,然后计算数学期
望即可.
【解答】解:(Ⅰ)由这名同学总得分X [﹣10,10],
可得X=﹣10,10,
∈
由题意可得P(|X|≤10)=P(X=﹣10)+P(X=10)=C 2×( )2×( )3+C 3×( )2×(
5 5
)3= ,
所以这名同学总分X [﹣10,10]的概率为 ;
(Ⅱ)由题可知总得∈分X的所有取值为﹣50,﹣30,﹣10,10,30,50,
P(X=﹣50)=C 0×( )0×( )5= ,
5
P(X=﹣30)=C 1×( )1×( )4= ,
5P(X=﹣10)=C 2×( )2×( )3= ,
5
P(X=10)=C 3×( )3×( )1= ,
5
P(X=30)=C 4×( )4×( )1= ,
5
P(X=50)=C 5×( )5×( )0= ,
5
所以X的分布列为:
X ﹣50 ﹣30 ﹣10 10 30 50
P
E(X)=(﹣50)× +(﹣30)× +(﹣10)× +30× +50× = ≈16.7,
故这名同学回答这5个问题的总得分的数学期望为16.7分.
【知识点】离散型随机变量及其分布列、离散型随机变量的期望与方差
22.由团中央学校部、全国学联秘书处、中国青年报社共同举办的 2018年度全国“最美中学生“寻访活动
结果出炉啦,此项活动于2018年6月启动,面向全国中学在校学生,通过投票方式寻访一批在热爱祖
国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中
学生”.现随机抽取了30名学生的票数,绘成如图所示的茎叶图,若规定票数在 65票以上(包括65
票)定义为风华组.票数在65票以下(不包括65票)的学生定义为青春组.
(Ⅰ)在这30名学生中,青春组学生中有男生7人,风华组学生中有女生12人,试问有没有90%的把握
认为票数分在青春组或风华组与性别有关;
(Ⅱ)如果用分层抽样的方法从青春组和风华组中抽取 5人,再从这5人中随机抽取2人,那么至少有1
人在青春组的概率是多少?
(Ⅲ)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机选取 4人,用 表
示所选4人中青春组的人数,试写出 的分布列,并求出 的数学期望. ξ
ξ ξ
附: ;其中n=a+b+c+d
独立性检验临界表:
P(K2>k ) 0.100 0.050 0.010
0
K 2.706 3.841 6.635【分析】(I)作出2×2列联表,求出k2≈1.83<2.706,从而没有90%的把握认为成绩分在青春组或风华组
与性别有关.
(Ⅱ) 用A表示“至少有1人在青春组”,利用对立事件概率计算公式能求出至少有1人在
青春组的概率.
(III)由题知,抽取的30名学生中有12名学生是青春组学生,抽取1名学生是青春组学生的
概率为 ,从所有的中学生中抽取 1名学生是甲组学生的概率是 , 服从二项分布
ξ
.由此能求出 的分布列、数学期望.
【解答】解:(I)作出2×2列联表:ξ
青春组 风华组 合计
男生 7 6 13
女生 5 12 17
合计 12 18 30
由列联表数据代入公式得 ,
因为1.83<2.706,
故没有90%的把握认为成绩分在青春组或风华组与性别有关.
(Ⅱ) 用A表示“至少有1人在青春组”,
则至少有1人在青春组的概率为 .
(III)由题知,抽取的30名学生中有12名学生是青春组学生,抽取1名学生是青春组学生的
概率为 ,
那么从所有的中学生中抽取1名学生是甲组学生的概率是 ,
又因为所取总体数量较多,抽取4名学生可以看出4次独立重复实验,于是 服从二项分布
. ξ
的取值为0,1,2,3,4.且 .
ξ所以得 的分布列为:
0 1 2 3 4
ξ
ξP
数学期望 .
【知识点】独立性检验、离散型随机变量的期望与方差、离散型随机变量及其分布列