文档内容
定远育才学校 2025-2026 学年高一(上)12 月月考
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A={x|x≥0},B={x|log x<1},则A∩B=( )
2
A. {x|00.
是( )
A. (−4,e) B. (−∞,e] C. [−4,l] D. [−4,e]
7.已知函数 ,若函数 恰有两个零点,则 的取值范围为( )
f(x)=21+ax−x(a>0) y=f(f(x))−x a1 1
A. (0, ) B. ( ,2) C. (0,1) D. (1,2)
eln2 eln2
8.《九章算术》是中国古代的数学名著,其中《方田》一章给出了弧田面积
⏜
的计算方法.弧田是由圆弧 和其对弦AB围成的图形,如图中阴影部分所示.若
AB
弧田所在圆的半径为√3,O为圆心,弦AB的长是3,则弧田的面积是( )
2√3π 3√3 π 3√3 3√3
A. B. 2π− C. − D. π−
3 2 2 8 4
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知x>0,y>0,且x+2y=2,则( )
4
A. xy的最小值是1 B. x2+ y2的最小值是
5
1 2
C. 2x+4y的最小值是4 D. + 的最小值是5
x y
10.已知函数y=f(x+1)是R上的偶函数,且f(x)在[1,+∞)上单调递增,a=f(log 8),b=f(−ln2),
2
,则下列说法正确的是( )
c=f(eln2
)
A. 函数y=f(x)的图象关于直线x=1对称
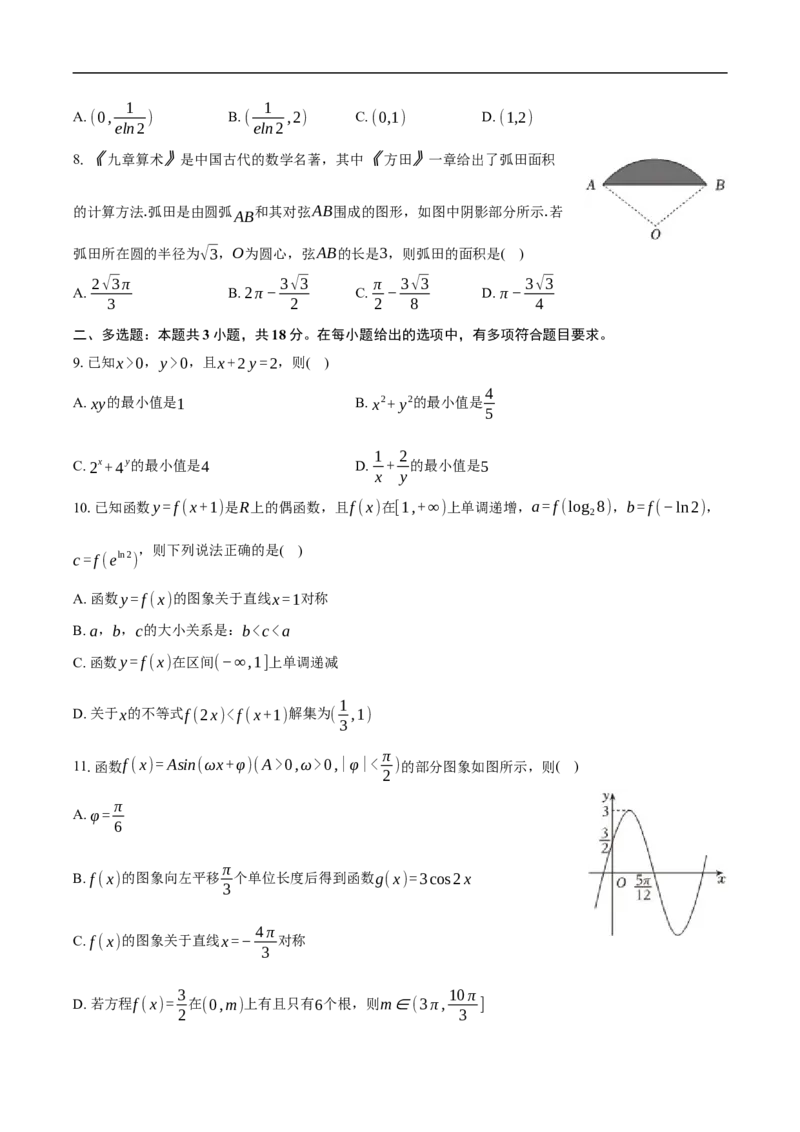
B. a,b,c的大小关系是:b0,ω>0,|φ|< )的部分图象如图所示,则( )
2
π
A. φ=
6
π
B. f(x)的图象向左平移 个单位长度后得到函数g(x)=3cos2x
3
4π
C. f(x)的图象关于直线x=− 对称
3
3 10π
D. 若方程f(x)= 在(0,m)上有且只有6个根,则m∈(3π, ]
2 3三、填空题:本题共3小题,每小题5分,共15分。
1 2
12.设正数a,b满足a+b=2,则 + 的最小值为 .
a b+1
x−a
13.已知f(x)= 是定义在R上的奇函数,则a= .
x2+4
14.已知奇函数 的定义域为 ,且为减函数,若满足 (3) ,则 的取值范围
f (x) (−2,2) f (x−1)+f <0 x
2
是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知集合A={x|a−20,
h(2)=f(2)−g(2)=5.980−5.241=0.738>0,
h(3)=f(3)−g(3)=7.651−6.892=0.759>0,
∴h(0)⋅h(1)<0,
由零点存在定理,得函数h(x)=f(x)−g(x)的零点存在区间为(0,1),故选:B.
π π 2π
5.D 【解析】若a=2kπ− ,b=2kπ+ ,k∈Z,则b−a取最小值为 ,A对,
2 6 3
5π π 4π
若a=2kπ− ,b=2kπ+ ,k∈Z,则b−a取最大值为 ,C对,
6 6 3
π 1
若a=2kπ− ,k∈Z,则sina=− ,若存在x∈[a,b],使f(x)=−1,则存在x∈[a,b],使
6 2
π
f(x)=1,与值域矛盾,则a不可能等于2kπ− ,k∈Z,B对,
67π π 1
若a=− ,b=− ,则值域为[−1, ],则D错,故选:D.
6 6 2
6.D 【解析】依题意,当x=0时,f(0)=1≥a×0=0恒成立,此时a∈R;①
1
当x<0时,f(x)=x2−2x+1≥ax恒成立,可转化为a≥(x+ −2) ,
x max
又当x<0时,−x>0,
1 √ 1 1 当且仅当 1,即 时取等号 ,
−x− ≥2 (−x)⋅ =2⇒x+ ≤−2( −x=− x=−1 )
x (−x) x x
1
所以当x<0时,(x+ −2) =−4,故a≥−4;②
x max
ex
当x>0时,f(x)=ex≥ax恒成立,可转化为a≤( ) ;
x min
令 ex ,则 (x−1)ex ,
g(x)= (x>0) g'(x)= (x>0)
x x2
当01时,g'(x)>0,
所以g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
故当x=1时,g(x)取得极小值,也是最小值,又g(1)=e,
即a≤e;③
由①②③,即−4≤a≤e.故选:D.
7. 【解析】由 ,得 ,
A f(f(x))−x=0 21+af(x)−f(x)−x=0
则 ,则 ,
21+af(x)−(21+ax−x)−x=0 21+af(x)=21+ax
所以1+af(x)=1+ax,
lnx
因为a>0,所以21+ax−x=x,所以a= .
xln2
lnx 1−lnx
令函数g(x)= ,则g'(x)= .
xln2 x2ln21−lnx
令g'(x)=0得,即 =0,解得x=e,
x2ln2
且当x∈(0,e)时,g'(x)>0;
当x∈(e,+∞)时,g'(x)<0.
所以g(x)在区间(0,e)上单调递增,在区间(e,+∞)上单调递减.
所以g(x)在x=e处取得极大值,也是最大值,
1
即g(x) =g(e)= ,
max eln2
又x趋近于+∞时,g(x)趋近于0,且当x>e时,g(x)>0,
1
所以g(x)的值域是(−∞, ).
eln2
lnx
函数y=f(f(x))−x恰有两个零点,即方程a= 有两根,
xln2
即y=a与y=g(x)的图象有两个交点,
1
所以a的取值范围是(0, ).故选:A.
eln2
8.D 【解析】依题意,AO=BO=√3,AB=3,
AO2+BO2−AB2 3+3−9 1
所以cos∠AOB= = =− ,
2AO⋅BO 2×√3×√3 2
2π
因为0<∠AOB<π,所以∠AOB= ,
3
⏜ 2π 2√3π
故AB=√3× = ,
3 3
1 2√3π 1 √3 3√3
则扇形AOB的面积为 × ×√3=π,△AOB的面积为 ×√3×√3× = ,
2 3 2 2 4
3√3
所以弧田的面积为π− .故选:D.
4
9.BC 【解析】对于A,由x>0,y>0,可得x+2y=2≥2√2xy,
1 1
化为xy≤ ,当且仅当x=2y=1,xy取得最大值 ,故A错误,
2 2对于B,x>0,y>0,且x+2y=2,
则x=2−2y,
4
x2+ y2=(2−2y) 2+ y2=5 y2−8 y+4≥ ,故B正确,
5
对于 , , ,且 ,则 ,
C x>0 y>0 x+2y=2 2x+4y≥2√2x ⋅4y=2√2x+2y=4
1
当且仅当x=1,y= 时等号成立,
2
∴2x+4y的最小值为4,故C正确,
对于D,∵x>0,y>0,x+2y=2,
1 2 1 1 2 2y 2x √2y 2x
∴ + = ( + )(x+2y)=5+ + ≥5+2 ⋅ =9,
x y 2 x y x y x y
2 2
当且仅当x= ,y= 时,等号成立,
3 3
1 2
∴ + 的最小值为9,故D错误.故选:BC.
x y
10.ACD 【解析】A中,由函数是y=f(x+1)上的偶函数,所以函数y=f(x+1)的图象关于y轴对称,
则函数f(x)的图象关于直线x=1对称,即f(x)=f(2−x),A正确;
C中,因为f(x)在[1,+∞)上单调递增,所以函数f(x)在(−∞,1]上单调递减,所以C正确;
D中,由于函数f(x)的图象关于直线x=1对称,且在[1,+∞)上单调递增,在(−∞,1]上单调递减,
故f(2x)2+ln2>2>1 f(2) ,即 > ,解得0<ω< ,
2 12 2ω 12 5
24k π
结合ω=2+ ,取k=0得ω=2,f(x)=3sin(2x+ ),所以A正确,
5 6
π π
将f(x)的图象向左平移 个单位长度后,可得f(x+ )的图象,
3 3
π π π 5π
根据f(x+ )=3sin[2(x+ )+ ]=3sin(2x+ )≠3cos2x,可知B不正确;
3 3 6 6
4π 4π π 5π
根据f(− )=3sin[2×(− )+ ]=3sin(− )=−3,达到最小值,
3 3 6 2
4π
可知f(x)的图象关于直线x=− 对称,所以C正确,
3
2π
根据f(x)的周期T= =π,
ω
π 4π 7π 10π 3
且f(0)=f( )=f(π)=f( )=f(2π)=f( )=f(3π)=f( )= ,
3 3 3 3 2
3 10π
可知:若f(x)= 在(0,m)上有且只有6个根,则m∈(3π, ],所以D正确.
2 3
故选:ACD.
3+2√2
12. 【解析】由a+b=2,可得a+(b+1)=3(因a,b>0,故a>0,b+1>1)
31 2 1 1 2 1 b+1 2a
则 + = [a+(b+1)]( + )= (3+ + ),
a b+1 3 a b+1 3 a b+1
b+1 2a √b+1 2a
其中 + ≥2 ⋅ =2√2,
a b+1 a b+1
b+1 2a
当且仅当 = (即(b+1) 2=2a2 )时取等号,
a b+1
结合a+b=2,解得a=3(√2−1),b=5−3√2,
1 2 3+2√2 3+2√2
故 + 的最小值为 .故答案为: .
a b+1 3 3
x−a
13.0 【解析】因为f(x)= 是定义在R上的奇函数,
x2+4
−a
所以f(0)= =0,解得a=0,
4
−x
当a=0时,f(−x)= =−f(x),即f(x)为奇函数.
(−x) 2+4
故答案为:0.
14.( 1 ) 【解析】 是奇函数,且满足 3 ,
− ,3 ∵f(x) f(x−1)+f( )<0
2 2
3 3
∴f(x−1)<−f( )=f(− )
2 2
∵f(x)在(−2,2)上是单调递减函数,
3 1
∴x−1>− ,且−20,解得: 或 ,所以定义域为 .
(1) x+1 x>1 x<−1 (−∞,−1)∪(1,+∞)
x+1≠0
(2)f(x)为奇函数,证明如下:
由(1)可知,定义域关于原点对称
−x−1 x+1 x−1 x−1
又f(−x)=log =log =log ( ) −1=−log =−f(x),
2 −x+1 2 x−1 2 x+1 2 x+1
所以f(x)为奇函数;
x−1 x+1−2 2
(3)因为f(x)=log =log =log (1− ),
2 x+1 2 x+1 2 x+1
2
又外部函数y=log u为增函数,内部函数y=1− 在[3,+∞)上为增函数,
2 x+1
由复合函数的单调性知函数f(x)在[3,+∞)上为增函数,3−1 1
所以f(x) =f(3)=log =log =−1,
min 2 3+1 22
又f(x)≥m对于x∈[3,+∞)恒成立,所以m≤[f(x)] ,所以m≤−1,
min
所以实数m的范围是(−∞,−1].
2ax
19.【解析】(1)因为f(x)= 在定义域[2b,b+3]上为奇函数,
x2+4
所以2b+b+3=0,解得b=−1,
a 2
1 2 = 1
又f( )= ,所以1 17,解得a= ;
2 17 +4 2
4
x
(2)由(1)得f(x)= ,x∈[−2,2],
x2+4
则f(x)在[−2,2]上单调递增,证明如下:
任取x ,x ∈[−2,2],且x 0,x2+4>0,x2+4>0
1 2 1 2 1 2
x x x (x2+4)−x (x2+4) (x −x )(4−x x )
则 f(x )−f(x )= 1 − 2 = 1 2 2 1 = 1 2 1 2 <0 ,
1 2 x2+4 x2+4 (x2+4)(x2+4) (x2+4)(x2+4)
1 2 1 2 1 2
所以f(x )−f(x )<0,即f(x )