文档内容
格致课堂
9.3 统计案例 公司员工的肥胖情况调查分析
(用时45分钟)
【选题明细表】
知识点、方法 题号
由统计信息解决实际问题 1,2,3,4,5,6,7,8,9,10,11,12
基础巩固
1.一组数据的方差为 ,平均数为 ,将这组数据中的每一个数都乘以2,所得的一组新数据的方差和平
均数分别为( )
A. , B. , C. , D. ,
【答案】C
【解析】设该组数据为 ,将这组数据中的每一个数都乘以2,则有 ,
平均数为 .又 ,则新数据的方差为
,
故选:C.
2.某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如
图所示.已知9时至10时的销售额为3万元,则9时至14时的销售总额为
A.10万元 B.12万元格致课堂
C.15万元 D.30万元
【答案】D
【解析】9时至10时的销售额频率为0.1,因此所有销售总额为 万元,故选D.
3.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个
最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
【答案】A
【解析】设9位评委评分按从小到大排列为 .
则①原始中位数为 ,去掉最低分 ,最高分 ,后剩余 ,
中位数仍为 , A正确.
②原始平均数 ,后来平均数
平均数受极端值影响较大, 与 不一定相同,B不正确
③
由②易知,C不正确.
④原极差 ,后来极差 可能相等可能变小,D不正确.
4.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名
著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼
梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学
生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )
A. B. C. D.格致课堂
【答案】C
【解析】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为
70÷100=0.7.故选C.
5.AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量
为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为
201,则下列叙述不正确的是( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是4月9日
C.这12天的AQI指数值的中位数是90
D.从4日到9日,空气质量越来越好
【答案】C
【解析】
由图可知, 不大于100天有6日到11日,共6天,所以A对,不选. 最小的一天为10日,所以B对,不
选.中位为是 ,C错.从图中可以4日到9日 越来越小,D对.所以选C.
6.甲、乙两套设备生产的同类型产品共48000件,采用分层随机抽样的方法从中抽取一个容量为80的样本
进行质量检测若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为________件.
【答案】18000
【解析】∵样本中有50件产品由甲设备生产,样本中有30件产品由乙设备生产,则乙设备生产的产品总数为
(件)
故答案为:
7.为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的认为格致课堂
作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互相不相同,则样本数据中的最大值为
.
【答案】10
【解析】设样本数据为:
若样本数据中的最大值为11,不妨设 ,由于样本数据互不相同,与
这是不可能成立的,若样本数据为4,6,7,8,10,代入验证知两式均成立,此时样本数据中的最大值为
10
8.在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下;分别求这17名运动员的成绩的
众数、中位数、平均数(保留到小数点后两位),并分析这些数据的含义.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
【答案】众数1.75m,中位数1.70m,平均数1.69m,含义见解析
【解析】在17个数据中,1.75出现了4次,次数最多,众数是1.75m.
将数据按从小到大的顺序排列,易知中位数是1.70m.
平均数是
这17名运动员的成绩的众数、中位数、平均数分别是1.75m,1.70m,1.69m.
众数是1.75m,说明跳1.75m的人数最多;中位数是1.70m,说明跳1.70m以下和70m以上的人数相等;
平均数是1.69m,说明所有参赛运动员的平均成绩是1.69m.
能力提升
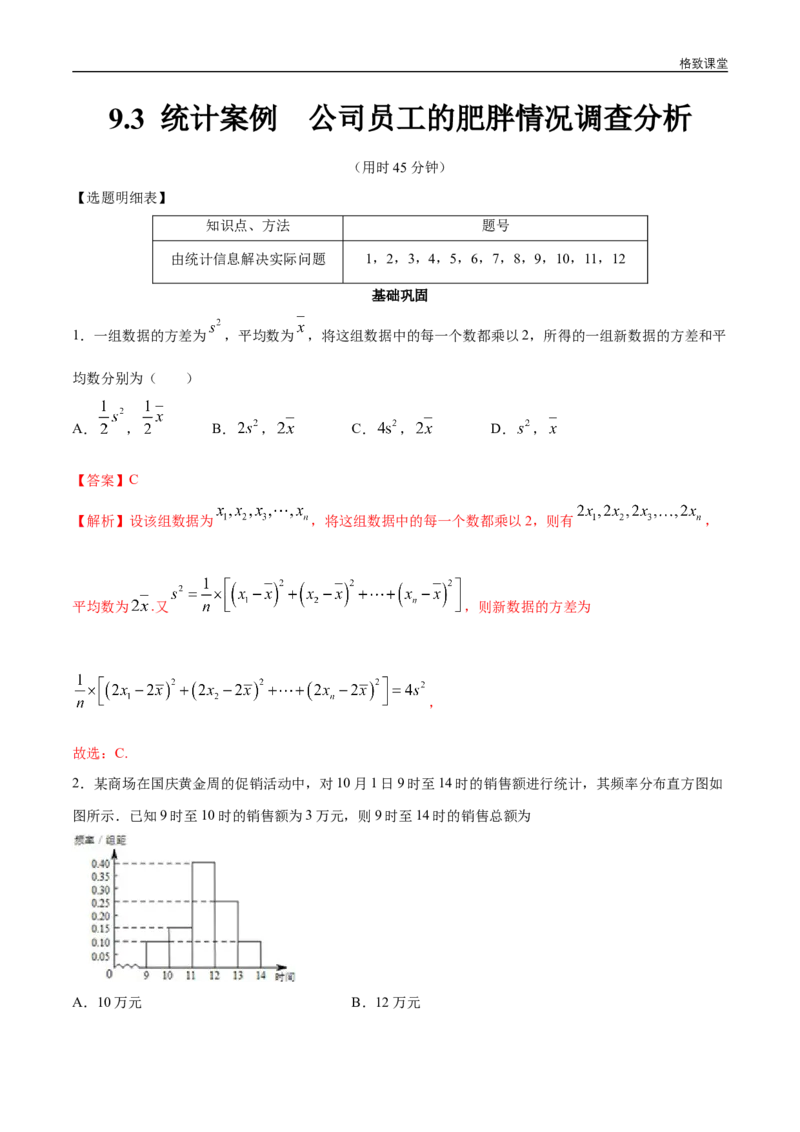
9.某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图
如图所示,由此估计此次考试成绩的中位数,众数和平均数分别是( )格致课堂
A.73.3,75,72 B.73.3,80,73
C.70,70,76 D.70,75,75
【答案】A
【解析】由频率分布直方图知,小于70的有24人,大于80的有18人,
则在[70,80]之间18人,所以中位数为70 73.3;
众数就是分布图里最高的小矩形底边的中点,即[70,80]的中点横坐标,是75;
平均数为45×0.05+55×0.15+65×0.20+75×0.30+85×0.25+95×0.05=72.
故选A.
10.某市有15个旅游景点,经计算,黄金周期间各个景点的旅游人数平均为20万,标准差为s,后来经核
实,发现甲、乙两处景点统计的人数有误,甲景点实际为20万,被误统计为15万,乙景点实际为18万,
被误统计成23万;更正后重新计算,得到标准差为s,则s与s 的大小关系为_____________.
1 1
【答案】s>s.
1
【解析】由已知,两次统计所得的旅游人数总数没有变,即两次统计的各景点旅游人数的平均数是相同的,
设为x,
则s=,
s=.
1
若比较s与s 的大小,只需比较(15-x)2+(23-x)2与(20-x)2+(18-x)2的大小即可.而(15-x)2+(23-
1
x)2=754-76x+2x2,(20-x)2+(18-x)2=724-76x+2x2,所以(15-x)2+(23-x)2>(20-x)2+(18-x)2.从而
s>s.
1
11.甲、乙两人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.格致课堂
(1)分别求出两人得分的平均数与方差;
(2)根据图和(1)中的计算结果,对两人的训练成绩作出评价.
【答案】(1)x =13,x =13,s=4,s=0.8.
甲 乙
(2)由s>s可知乙的成绩较稳定.从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的
成绩在不断提高,而乙的成绩则无明显提高.
【解析】(1)由图可得甲、乙两人五次测试的成绩分别为
甲:10,13,12,14,16;
乙:13,14,12,12,14.
x ==13,
甲
x ==13,
乙
s=×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
s=×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
(2)由s>s可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则
无明显提高.
素养达成
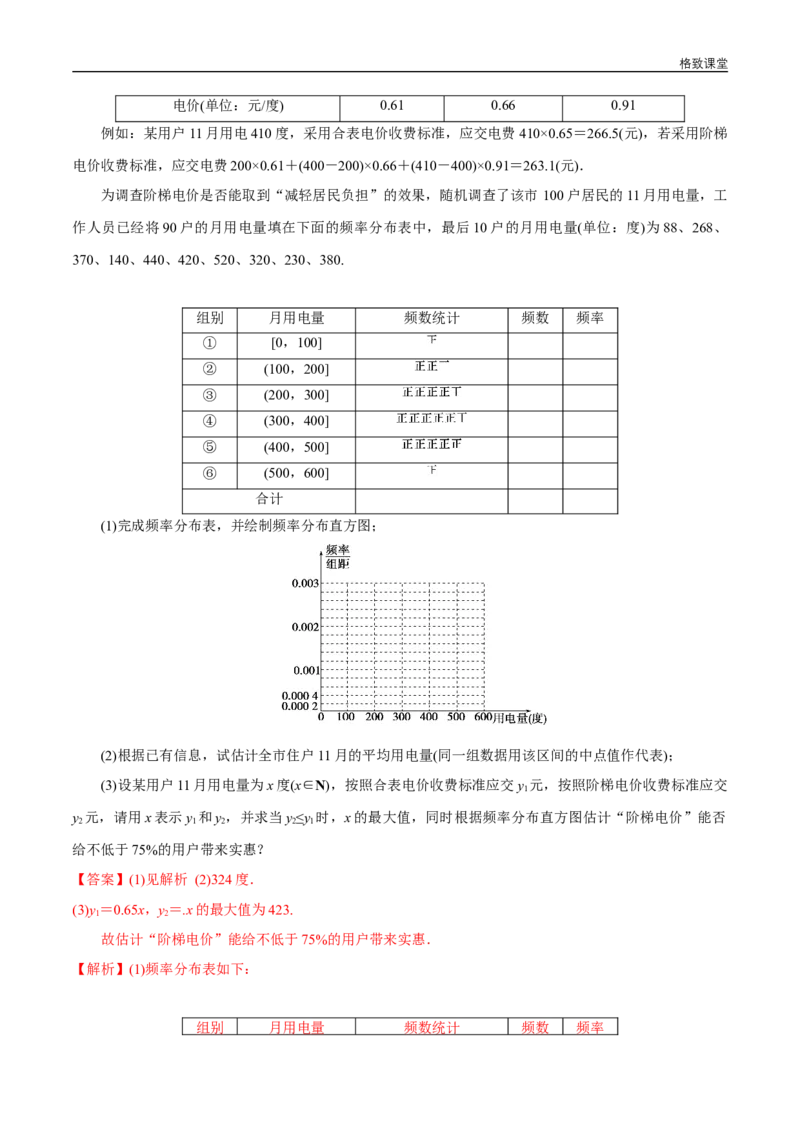
12.为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程.非一户一表用户电费采用
“合表电价”收费标准:0.65元/度.“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执
行非夏季标准如下:
第一档 第二档 第三档
每户每月用电量
[0,200] (200,400] (400,+∞)
(单位:度)格致课堂
电价(单位:元/度) 0.61 0.66 0.91
例如:某用户11月用电410度,采用合表电价收费标准,应交电费410×0.65=266.5(元),若采用阶梯
电价收费标准,应交电费200×0.61+(400-200)×0.66+(410-400)×0.91=263.1(元).
为调查阶梯电价是否能取到“减轻居民负担”的效果,随机调查了该市 100户居民的11月用电量,工
作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量(单位:度)为88、268、
370、140、440、420、520、320、230、380.
组别 月用电量 频数统计 频数 频率
① [0,100]
② (100,200]
③ (200,300]
④ (300,400]
⑤ (400,500]
⑥ (500,600]
合计
(1)完成频率分布表,并绘制频率分布直方图;
(2)根据已有信息,试估计全市住户11月的平均用电量(同一组数据用该区间的中点值作代表);
(3)设某用户11月用电量为x度(x∈N),按照合表电价收费标准应交y 元,按照阶梯电价收费标准应交
1
y 元,请用x表示y 和y ,并求当y≤y 时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否
2 1 2 2 1
给不低于75%的用户带来实惠?
【答案】(1)见解析 (2)324度.
(3)y=0.65x,y=.x的最大值为423.
1 2
故估计“阶梯电价”能给不低于75%的用户带来实惠.
【解析】(1)频率分布表如下:
组别 月用电量 频数统计 频数 频率格致课堂
① [0,100] 4 0.04
② (100,200] 12 0.12
③ (200,300] 24 0.24
④ (300,400] 30 0.30
⑤ (400,500] 26 0.26
⑥ (500,600] 4 0.04
合计 100 1
频率分布直方图如图:
(2)该100户用户11月的平均用电量
x=50×0.04+150×0.12+250×0.24+350×0.3+450×0.26+550×0.04=324(度),
所以估计全市住户11月的平均用电量为324度.
(3)y=0.65x,
1
y=.
2
由y≤y 得或
2 1
或,
解得x≤≈423.1.
因为x∈N,故x的最大值为423.
根据频率分布直方图,x≤423时的频率为0.04+0.12+0.24+0.3+23×0.002 6=0.759 8>0.75,
故估计“阶梯电价”能给不低于75%的用户带来实惠.