文档内容
领取更多免费资料关注微信公众号:网盘网课资源
决胜 2024 年高考数学押题预测卷 03
数 学
(新高考九省联考题型)
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己
的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知向量 , ,若 ,则 ( )
A. B. C. D.
2.已知集合 , ,则下列结论正确的是( )
A. B. C. D.
3.已知 , , ,则( )
A. B. C. D.
4.已知样本数据 的平均数为 ,则数据 ( )
A. 与原数据的极差不同 B. 与原数据的中位数相同
C. 与原数据的方差相同 D. 与原数据的平均数相同
5.在梯形 中, ,以下底 所在直线为
轴,其余三边旋转一周形成的面围成一个几何体,则该几何体的体积为( )
A. B. C. D.
6.甲箱中有2个白球和4个黑球,乙箱中有4个白球和2个黑球.先从甲箱中随机取出一球放入乙箱
中,以 , 分别表示由甲箱中取出的是白球和黑球;再从乙箱中随机取出一球,以B表示从乙箱中
取出的是白球,则下列结论错误的是( )
A. , 互斥 B. C. D.
7.已知函数 的定义域为 , 是偶函数, 是奇函数,则 的
最小值为( )
A. B. C. D.
8.双曲线C: 的左、右焦点分别是 , ,离心率为 ,点 是C的
1领取更多免费资料关注微信公众号:网盘网课资源
右支上异于顶点的一点,过 作 的平分线的垂线,垂足是M, ,若C上一点T满
足 ,则T到C的两条渐近线距离之和为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数 是关于x的方程 的两根,则( )
A. B.
C. D. 若 ,则
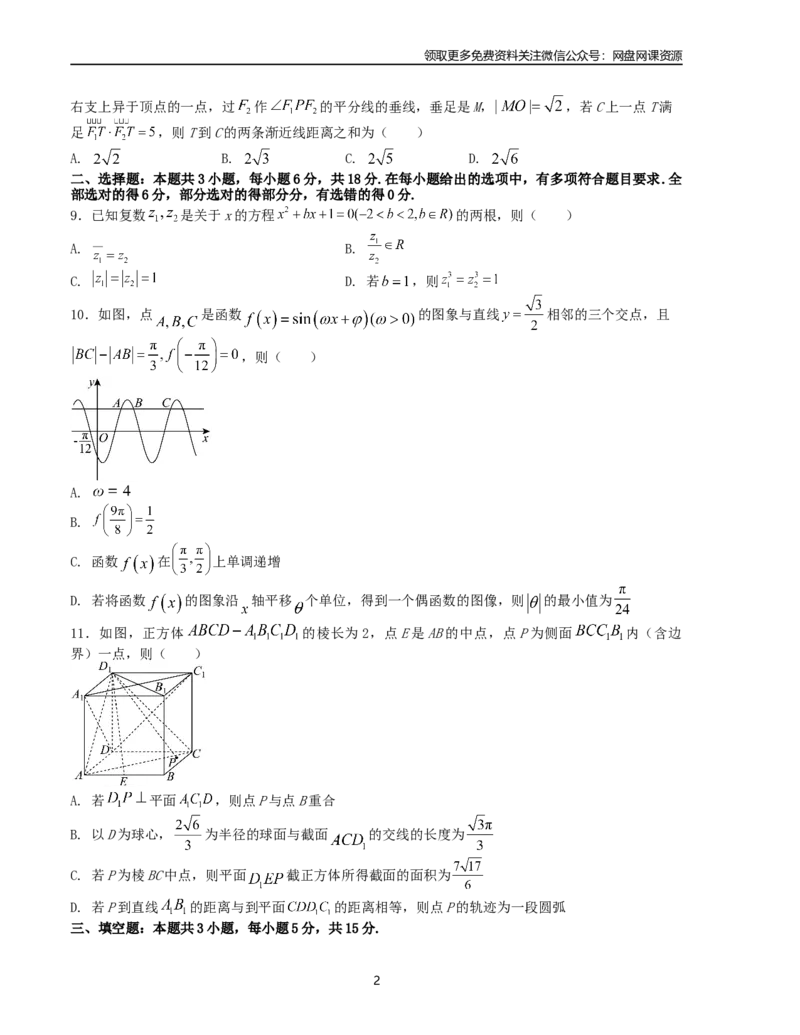
10.如图,点 是函数 的图象与直线 相邻的三个交点,且
,则( )
A.
B.
C. 函数 在 上单调递增
D. 若将函数 的图象沿 轴平移 个单位,得到一个偶函数的图像,则 的最小值为
11.如图,正方体 的棱长为2,点E是AB的中点,点P为侧面 内(含边
界)一点,则( )
A. 若 平面 ,则点P与点B重合
B. 以D为球心, 为半径的球面与截面 的交线的长度为
C. 若P为棱BC中点,则平面 截正方体所得截面的面积为
D. 若P到直线 的距离与到平面 的距离相等,则点P的轨迹为一段圆弧
三、填空题:本题共3小题,每小题5分,共15分.
2领取更多免费资料关注微信公众号:网盘网课资源
12. 的展开式中的常数项为__________.(用数字作答).
13.在 中, , ,则 __________; __________.
14.已知点A为抛物线 上一点(点A在第一象限),点F为抛物线的焦点,准线为l,线段AF
的中垂线交准线l于点D,交x轴于点E(D、E在AF的两侧),四边形 为菱形,若点P、Q分
别在边 DA、EA上, , ,若 则 的最小值为______,
的最小值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.设 ,曲线 在点 处取得极值.
求a;
求函数 的单调区间和极值.
16.如图,四棱锥 中,底面 是边长为2的菱形, ,平面 底面
.
(1)求证: ;
(2)若 ,且四棱锥 的体积为2,求直线 与平面 所成角的正弦值.
17.现有标号依次为1,2,…,n的n个盒子,标号为1号的盒子里有2个红球和2个白球,其余盒子
里都是1个红球和1个白球.现从1号盒子里取出2个球放入2号盒子,再从2号盒子里取出2个球放
入3号盒子,…,依次进行到从 号盒子里取出2个球放入n号盒子为止.
3领取更多免费资料关注微信公众号:网盘网课资源
(1)当 时,求2号盒子里有2个红球的概率;
(2)当 时,求3号盒子里的红球的个数 的分布列;
(3)记n号盒子中红球的个数为 ,求 的期望 .
18.已知 为曲线 上任意一点,直线 与圆 相切,且分别与
交于 两点, 为坐标原点.
(1)若 为定值,求 的值,并说明理由;
(2)若 ,求 面积的取值范围.
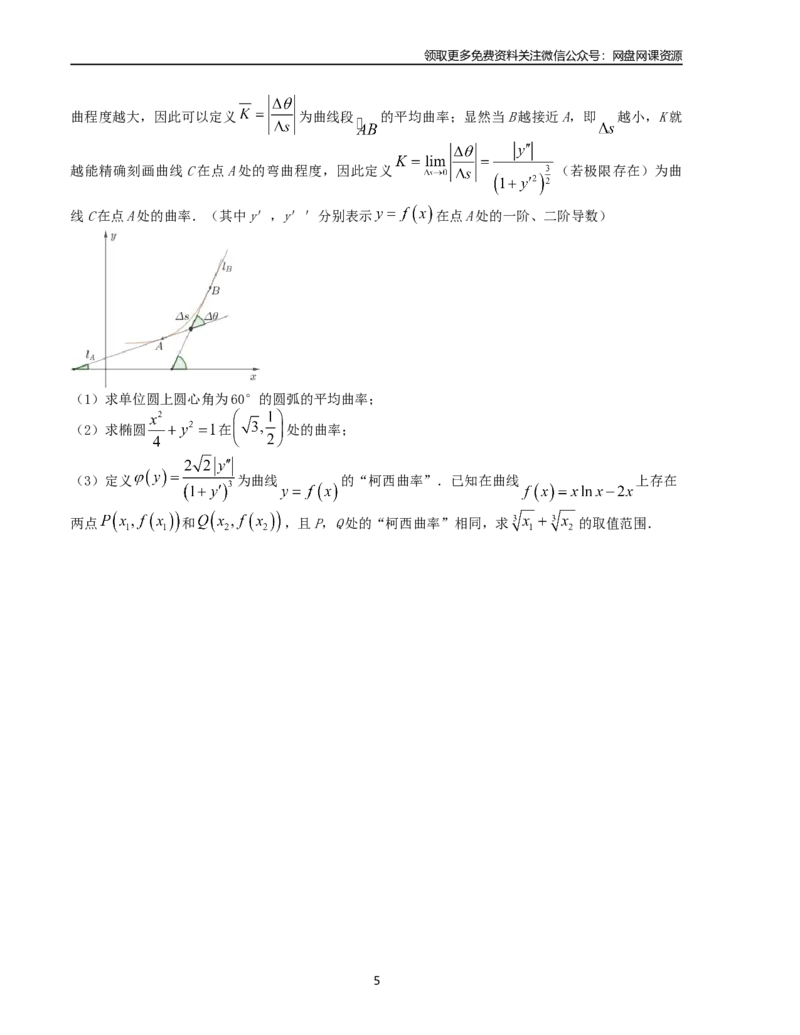
19.在几何学常常需要考虑曲线的弯曲程度,为此我们需要刻画曲线的弯曲程度.考察如图所示的光
滑曲线C: 上的曲线段 ,其弧长为 ,当动点从A沿曲线段 运动到B点时,A点的
切线 也随着转动到B点的切线 ,记这两条切线之间的夹角为 (它等于 的倾斜角与 的倾斜
角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯
4领取更多免费资料关注微信公众号:网盘网课资源
曲程度越大,因此可以定义 为曲线段 的平均曲率;显然当B越接近A,即 越小,K就
越能精确刻画曲线C在点A处的弯曲程度,因此定义 (若极限存在)为曲
线C在点A处的曲率.(其中y',y''分别表示 在点A处的一阶、二阶导数)
(1)求单位圆上圆心角为60°的圆弧的平均曲率;
(2)求椭圆 在 处的曲率;
(3)定义 为曲线 的“柯西曲率”.已知在曲线 上存在
两点 和 ,且P,Q处的“柯西曲率”相同,求 的取值范围.
5