文档内容
高一第二学期期末数学试卷
一、选择题(共8小题).
1. 已知向量 , ,若 ,那么m的值为( )
A. B. C. 2 D.
【答案】C
【解析】
【分析】
由两个向量垂直得数量积等于零,列方程可求出m的值
【详解】向量 , ,
若 ,则 ,
即 ,
解得 .
故选:C.
【点睛】此题考查由向量垂直求参数,属于基础题
2. 的值等于( )
A. B. C. D.
【答案】D
【解析】
【分析】
利用和角的正弦公式化简求值得解.
【详解】由题得 .
故选:
【点睛】本题主要考查和角的正弦公式的应用,意在考查学生对这些知识的理解掌握水平,属于基础题.3. 已知圆柱的底面半径和高都是 ,那么圆柱的侧面积是( )
A. B. C. D.
【答案】B
【解析】
【分析】
本题可根据圆柱的侧面积公式得出结果.
【详解】因为圆柱的底面半径和高都是 ,
所以圆柱的侧面积 ,
故选:B.
【点睛】本题考查圆柱的侧面积的计算,若圆柱的底面半径为 ,高为 ,则侧面积 ,考查计算
能力,是简单题.
4. 给出下列四个命题:①垂直于同一平面的两个平面互相垂直;②平行于同一平面的两个平面互相平行;
③垂直于同一直线的两个平面互相垂直;④平行于同一直线的两个平面互相平行,其中正确命题的序号是
( )
A. ① B. ② C. ③ D. ④
【答案】B
【解析】
【分析】
通过举例的方式逐一验证各选项的对错.
【详解】①垂直于同一平面的两个平面可能垂直,也可能平行,比如正方体的下底面和左右侧面互相垂直,
但是左右侧面互相平行,故错误;
②平行于同一平面的两个平面互相平行,比如用平行于正方体上下底面的平面截正方体,所得截面和上下
底面互相平行,故正确;
③垂直于同一直线的两个平面互相平行,比如正方体的一条侧棱垂直于上下底面,且上下底面互相平行,
故错误;
④平行于同一直线的两个平面可能相交,比如正方体的下底面的一条棱平行于侧面和上底面,而侧面和上
底面相交,故错误.
故选:B.
【点睛】本题考查空间直线、平面的位置关系的判断,常用的方法是采用作图或举例子的方式去判断对应
命题的真假,主要是考查学生的空间想象能力,难度一般.5. 化简向量 等于( )
A. B. C. D.
【答案】A
【解析】
【分析】
直接利用向量的加减法法则求解即可
【详解】 .
故选:A.
【点睛】此题考查向量的加减法法则的应用,属于基础题
6. 关于函数 ,下列命题正确的是( )
A. 存在 ,使 是偶函数 B. 对任意的 , 都是非奇非偶函数
C. 存在 ,使 既是奇函数,又是偶函数 D. 对任意的 , 都不是奇函数
【答案】A
【解析】
【分析】
由三角函数的图象性质结合诱导公式,对每一选项进行逐一判断即可.
【详解】对于A,当 , 时,函数 是偶函数,所以A正确;
对于B,当 , 时,函数 是奇函数,所以B错误;
对于C,由选项A, B的分析,不存在 ,使函数 既是奇函数,又是偶函数,所以C错误;
对于D, , 时,函数 是奇函数,所以D错误.
故选:A.
【点睛】本题考查三角函数的奇偶性的分析,属于基础题.
7. 已知非零向量 、 满足 ,且 ,那么 等于( )A. B. C. D.
【答案】C
【解析】
【分析】
本题首先可根据 得出 ,然后根据 得出 ,即可求出 的值.
【详解】因为非零向量 、 满足 ,且 .
所以 , , ,
故选:C.
【点睛】本题考查向量的运算,考查向量的模的相关性质,考查计算能力,体现了基础性,是简单题.
8. 已知函数 ,如果存在实数 , ,使得对任意 的实数x,都有
,那么 的最小值为( )
A. B. C. D.
【答案】D
【解析】
【分析】
由题意分析可知 为 的最小值, 为 的最大值,故 最小时为半个周期.
【详解】 的周期 ,
由题意可知 为 的最小值, 为 的最大值,的最小值为 .
故选:D.
【点睛】本题考查三角函数的图象及性质,属于简单题,分析清楚题目意思是关键.
二、填空题(本大题共6小题,每小题5分,共30分.请把答案填在答题卡中相应题中横线
上)
9. 等于________.
【答案】
【解析】
【分析】
直接逆用余弦的二倍角公式求解即可
【详解】 ,
故答案为: .
【点睛】此题考查余弦的二倍角公式的应用,属于基础题
10. 已知 ,且 ,那么 等于________; 等于________.
【答案】 (1). (2).
【解析】
【分析】
给 等 式 两 边 平 方 , 再 利 用 正 弦 的 二 倍 角 公 式 可 求 出 , 而
,从而可求出 的值
【详解】 ,且 , , .把所给的等式平方可得 , .
再根据 .
求得 ,或 (舍去),
故答案为: ; .
【点睛】此题考查同角三角函数的关系的应用,考查二倍角公式的应用,考查转化思想,属于基础题
11. 在 中, ,且 ,则边AB的长为 .
【答案】1
【解析】
试题分析:因为 ,所以
考点:向量数量积
12. 在 中,角A、B、C对边分别为a、b、c,已知 , , ,那么b等于
________.
【答案】
【解析】
【分析】
由三角形面积公式求出边 ,再由余弦定理计算可得;
【详解】解: , , ,
,
由余弦定理可得 .
故答案为: .【点睛】本题考查余弦定理及三角形面积公式的应用,属于基础题.
13. 在 中,角A,B,C所对的边分别为a,b,c,如果 , , ,那么 的
最大内角的余弦值为________.
【答案】
【解析】
【分析】
由边的大小关系可知 是最大角,然后利用余弦定理求解.
【详解】角A,B,C所对的边分别为a,b,c,如果 , , ,则 是最大角,
则 ,
故答案为: .
【点睛】本题考查三角形中的边角关系,考查余弦定理的应用,属于简单题.
14. 已知 , , , ,如果P点是 所在平面内一点,且
,那么 的值等于________.
【答案】13
【解析】
【分析】
由条件可得 , ,可得 ,由 ,
可得出答案.
【详解】 , , , ,, ,
,
, ,
又 ,
.
故答案为:13.
【点睛】本题主要考查了平面向量线性运算和数量积的运算性质的应用,属于中档题.
三、解答题(本大题共6小题,共80分解答应写出文字说明,证明过程或演算步骤.)
15. 已知向量 , .
(1)若 , 共线,求x的值;
(2)若 ,求x的值;
(3)当 时,求 与 夹角 的余弦值.
【答案】(1) ;(2) ;(3) .
【解析】
【分析】
(1)利用向量共线的坐标表示即可求解;
(2)分别求出 和 的坐标,利用向量垂直的坐标表示即可求解;
(3)利用向量夹角的公式即可求解.
【详解】(1) , 共线,
,解得 ;(2) ,且 ,
,解得 ;
(3)当 时, ,
, , ,
.
【点睛】本题主要考查了向量共线、向量垂直。以及向量夹角的坐标表示,属于基础题.
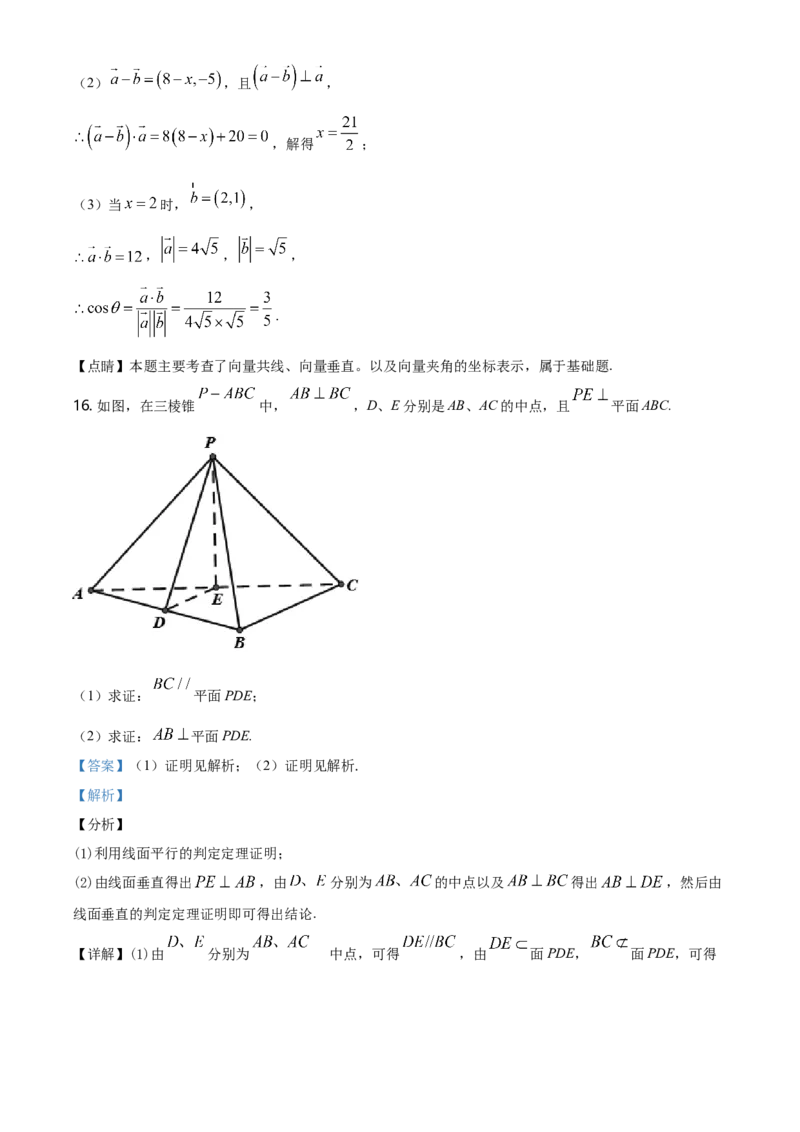
16. 如图,在三棱锥 中, ,D、E分别是AB、AC的中点,且 平面ABC.
(1)求证: 平面PDE;
(2)求证: 平面PDE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
【分析】
(1)利用线面平行的判定定理证明;
(2)由线面垂直得出 ,由 分别为 的中点以及 得出 ,然后由
线面垂直的判定定理证明即可得出结论.
【详解】(1)由 分别为 的中点,可得 ,由 面PDE, 面PDE,可得平面PDE;
(2)由 平面ABC, 平面ABC,可得 ,由(1)知 ,且由题意 可得
,所以由 ,且 平面PDE,可得 平面PDE.
【点睛】本题考查了线面平行的证明,考查了线面垂直的性质定理和判定定理的应用,属于一般难度的题.
17. 已知函数 .
(1)求 的最小正周期;
(2)求 在区间 上的最大值和最小值;
(3)若函数 在 上有两个不同的零点,求实数k的取值范围.
【答案】(1) ;(2)最大值为2,最小值为 ;(3) .
【解析】
【分析】
(1)先利用二倍角公式和辅助角公式对函数化简,再利用周期公式可求出周期;
(2)由 得 ,再结合正弦函数的图像和性质可求出函数的最值;
(3)由函数 在 上单调递增, ,在 上单调递减, ,从
而可求出实数k的取值范围.
【详解】(1)由 ,
得 的最小正周期为 .(2)因为 ,
所以 ,
所以 .
.
从而
所以,当 ,即 时, 的最大值为2;
当 ,即 时, 的最小值为 .
(3)由 ,得 ,而函数 在 上单调递增,
,在 上单调递减, ,
所以若函数 在 上有两个不同的零点,则 .
【点睛】此题考查三角函数恒等变换公式的应用,考查正弦函数图像和性质的应用,属于基础题
18. 在 中,角A,B,C的对边分别是a,b,c, , .
(1)求边c的值;
(2)若 ,求 的面积.
【答案】(1)4;(2) .
【解析】
【分析】
(1)运用正弦定理,角化为边,即可得到所求值;(2)运用余弦定理求得 ,可得 ,再由面积公式即可得到所求值.
【详解】(1) ,
由正弦定理可得, ;
(2) ,
代入 , ,
解出 ,
,
.
【点睛】本题考查三角形的正弦定理和余弦定理、面积公式的运用,考查运算能力,属于中档题.
19. 已知 , .
(1)求 的值;
(2)求 的值;
(3)若 且 ,求 的值.
【答案】(1) ;(2) ;(3) .
【解析】
【分析】
(1)根据角的范围,利用平方关系求出 ,再利用商的关系求 的值;(2)直接利用两角和的正切公式求 的值;
(3)求出 ,由 ,利用两角差的正弦公式求解即可.
【详解】(1)因为 , ,
故 ,所以 .
(2) .
(3)因为 , ,所以 .
又因为 ,所以 .
.
【点睛】三角函数求值有三类,(1)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,
但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并
且消除非特殊角的三角函数而得解.(2)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角
函数值,解题关键在于“变角”,使其角相同或具有某种关系.(3)“给值求角”:实质是转化为“给值求值”,
先求角的某一函数值,再求角的范围,确定角.
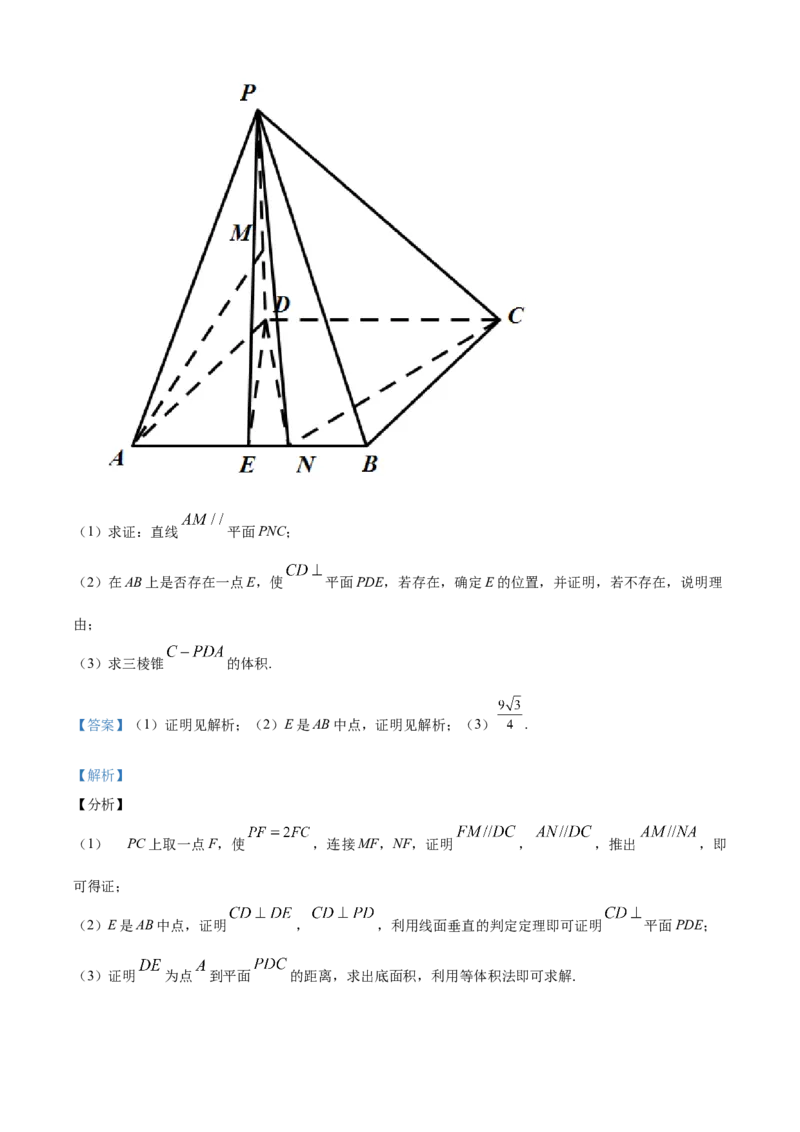
20. 如图,在四棱锥 中,底面ABCD是菱形, , 平面ABCD,
, , .(1)求证:直线 平面PNC;
(2)在AB上是否存在一点E,使 平面PDE,若存在,确定E的位置,并证明,若不存在,说明理
由;
(3)求三棱锥 的体积.
【答案】(1)证明见解析;(2)E是AB中点,证明见解析;(3) .
【解析】
【分析】
(1) 在PC上取一点F,使 ,连接MF,NF,证明 , ,推出 ,即
可得证;
(2)E是AB中点,证明 , ,利用线面垂直的判定定理即可证明 平面PDE;
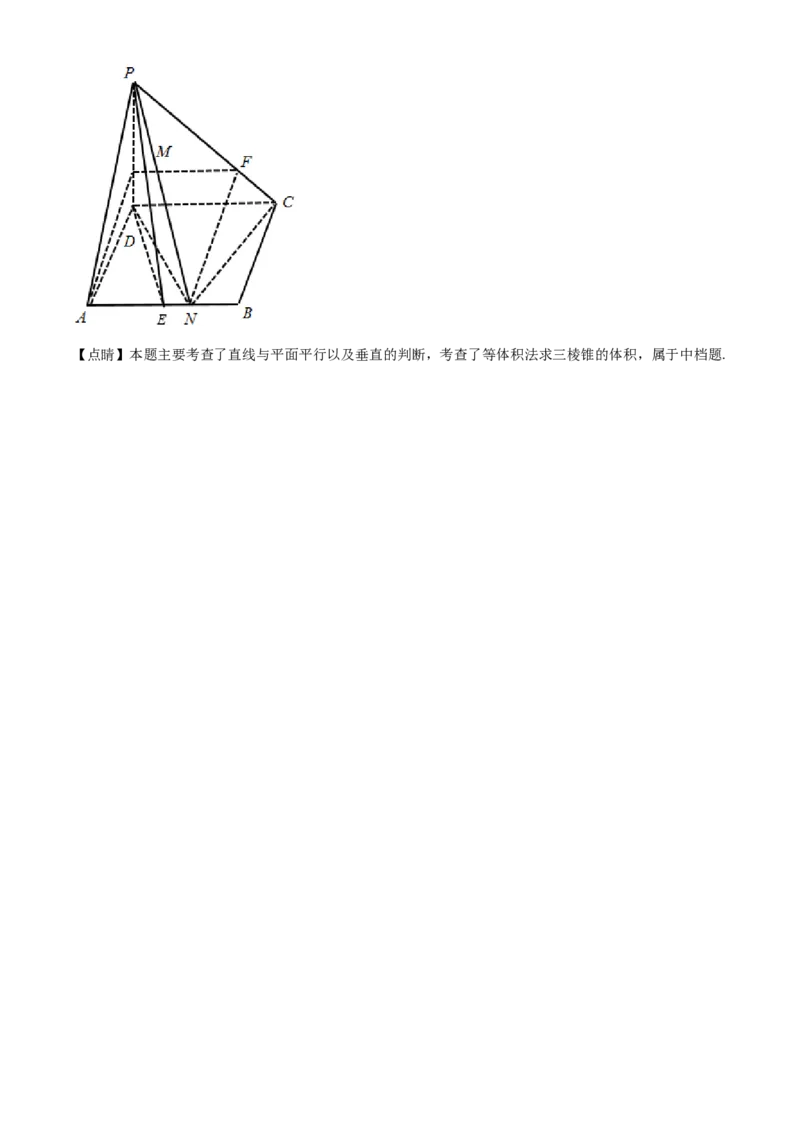
(3)证明 为点 到平面 的距离,求出底面积,利用等体积法即可求解.【详解】(1)在PC上取一点F,使 ,连接MF,NF,因为 , ,所以
, , , ,
可得 且 .
所以MFNA为平行四边形,
即 ,
又 平面 ,
.
所以直线 平面
(2)E是AB中点,证明如下:
因为E是AB中点,底面ABCD是菱形, ,所以 ,
因为 ,所以, 即 ,
又 平面ABCD,所以 ,
又 ,
所以直线 平面PDE
(3)直线 ,且由(2)可知,DE为点A到平面PDC的距离, ,
,
所以 .【点睛】本题主要考查了直线与平面平行以及垂直的判断,考查了等体积法求三棱锥的体积,属于中档题.