文档内容
第二学期期末考试试卷
高一数学
本试卷共4页,满分150分,考试时间120分钟.
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一
项是符合要求的,把答案填在答题卡上.
1. 已知 的值等于( )
A. B.
C. D.
【答案】B
【解析】
【分析】
利用两角和与差的正弦公式求得答案.
【详解】 .
故选:B.
【点睛】本题主要考查了两角和与差的正弦函数公式.属于基础题.
2. 若 , ,则 ( )
A. B.
C. D.
【答案】A
【解析】
【分析】
由两角差的正切公式直接计算.
【详解】由 ,故选:A
【点睛】本题考查两角差的正切公式,直接利用公式计算即可,本题属于基础题.
3. 与角 终边相同的角为( )
A. B.
C. D.
【答案】C
【解析】
【分析】
根据终边相同角的概念,可写出与 终边相同角,调整参数即可求解答案.
【详解】与角 终边相同的角可写成
令 ,则
故选:C
【点睛】本题考查终边相同角的概念,属于基础题.
4. 已知向量 , ,满足 ,则 ( )
A. 1 B. C. 4 D.
【答案】D
【解析】
【分析】
由向量平行的坐标运算求解即可.
【详解】向量 , ,,
故选:D
【点睛】本题主要考查了由向量平行求参数,属于基础题.
5. 若角 终边经过点 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据角度终边上点的坐标,即可容易求得结果.
【详解】因为角 终边经过点 ,
则 .
故选:C.
【点睛】本题考查由角度终边上的一点求三角函数值,属基础题.
6. 已知向量 , ,且 ,则 的坐标可以为( )
A. B.
C. D.
【答案】B
【解析】
【分析】
设 的坐标,然后根据 以及 ,简单计算,可得结果.
【详解】设
由 ,且 ,所以 ①
又 ,所以 ②由①②可知: 或
故向量 或
故选:B
【点睛】本题考查向量的坐标运算,重在计算,属基础题.
7. 棱长为3的正方体的8个顶点均在同一个球面上,则此球的体积为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
先求得正方体的对角线长为 ,根据球的直径等于长方体的对角线长,求得球的半径,结合体积公
式,即可求解.
【详解】由题意,棱长为3的正方体的对角线长为 ,
设外接球的半径为 ,
根据组合体的性质,可得 ,即 ,
所以球的体积为 .
故选:D.
【点睛】本题主要考查球的体积的计算,以及组合体的性质,其中解答中熟记组合体的性质,求得球的半
径是解答的关键,着重考查推理与运算能力.
8. 非零向量 满足 且 与 夹角为 ,则“ ”是“ ”的( )
A. 必要而不充分条件 B. 充分而不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】C【解析】
【分析】
由题意,若 ,根据向量的数量积和模的计算公式,可得 ,得到 ,;反之也可求
得 ,即可得到答案.
【详解】由题意,非零向量 满足 且 与 夹角为 ,
若 ,即 ,
解得 ,又因为 ,可得 ,即充分性是成立的;
若 ,由 ,可得 ,即必要
性是成立的,
所以“ ”是“ ”的充分必要条件.
故选:C.
【点睛】本题主要考查了充分条件、必要条件的判定,其中解答中熟记向量的数量积的运算,以及向量的
模的运算公式是解答的关键,着重考查了推理与运算能力.
9. 若函数 的图象向右平移 个单位长度得到函数 的图象,若函数 在区间 上
单调递增,则 的最大值为( ).
A. B. C. D.
【答案】C
【解析】
【分析】
由题意利用函数 的图象变换规律,正弦函数的单调性,求出 的最大值.【详解】解:把函数 的图象向右平移 个单位长度得到函数 的图象,
若函数 在区间 , 上单调递增,
在区间 , 上, , ,
则当 最大时, ,求得 ,
故选:C.
【点睛】本题主要考查函数 的图象变换规律,正弦函数的单调性,属于基础题.
10. 已知一个正方体和一个圆柱等高,并且侧面积相等,则这个正方体和圆柱的体积之比为( )
A. B.
.
C D.
【答案】B
【解析】
【分析】
设正方体的棱长为 ,根据侧面积相等,可得圆柱的底面半径为 ,再根据体积公式可得答案.
【详解】设正方体的棱长为 ,则圆柱的高为 ,设圆柱的底面半径为 ,
则正方体的侧面积为 ,圆柱的侧面积为 ,
所以 ,所以 ,
所以正方体和圆柱的体积之比为 .
故选:B.
【点睛】本题考查了正方体和圆柱的侧面积与体积公式,属于基础题.
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.11. 一个圆锥的母线长为 ,母线与轴的夹角为 ,则圆锥底面半径为________.
【答案】 ;
【解析】
【分析】
作出圆锥的轴截面图,结合直角三角形边角关系,即可求解.
【详解】解:如图所示为圆锥的轴截面, ,
所以圆锥底面半径 ,故答案为:5.
【点睛】本题考查圆锥的结构特征,属于基础题.
12. 已知单位向量 , 的夹角为 ,则 与 的夹角为________.
【答案】 ;
【解析】
【分析】
根据平面向量的夹角公式计算可得.
【详解】因为单位向量 , 的夹角为 ,
所以 ,
所以 ,
设 与 的夹角为 ,则 .
又 ,所以 .
故答案为: .
【点睛】本题考查了平面向量的夹角公式,属于基础题.
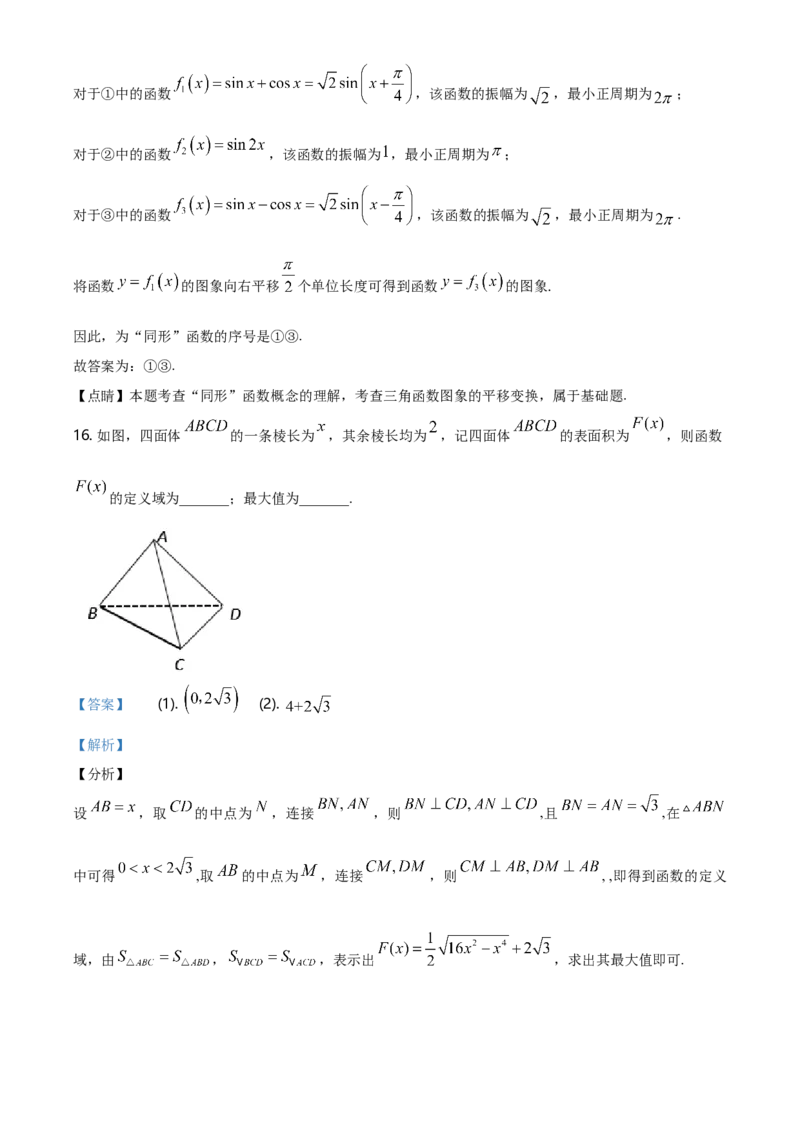
13. 已知函数 的部分图象如图所示,则 的最小正周期为______.
【答案】
【解析】【分析】
观察图象,可列式 ,解得结果即可.
【详解】设 的最小正周期为 ,
由图可知, ,解得 .
故答案为: .
【点睛】本题考查了由三角函数的图象求最小正周期,属于基础题.
14. 在△ 中,已知 ,则 的形状为______.
【答案】直角三角形
【解析】
【分析】
设 ,则 , ,由勾股定理可判断出三角形的形状.
【详解】解:设 ,则 , ,因为 ,所以为直角三角形,
故答案为: 直角三角形.
【点睛】本题考查了勾股定理的应用,属于基础题.
15. 若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数.给出下列三个函数:
① ;② ;③ .
其中,为“同形”函数的序号是_______.
【答案】①③
【解析】
【分析】
将①③中的函数解析式化简,根据“同形”函数的定义可知,两个函数的振幅相等,最小正周期也相等,
由此可得出结论.
【详解】根据“同形”函数的定义可知,若两个函数互为“同形”函数,则两个函数的振幅相等,最小正
周期也相等,对于①中的函数 ,该函数的振幅为 ,最小正周期为 ;
对于②中的函数 ,该函数的振幅为 ,最小正周期为 ;
对于③中的函数 ,该函数的振幅为 ,最小正周期为 .
将函数 的图象向右平移 个单位长度可得到函数 的图象.
因此,为“同形”函数的序号是①③.
故答案为:①③.
【点睛】本题考查“同形”函数概念的理解,考查三角函数图象的平移变换,属于基础题.
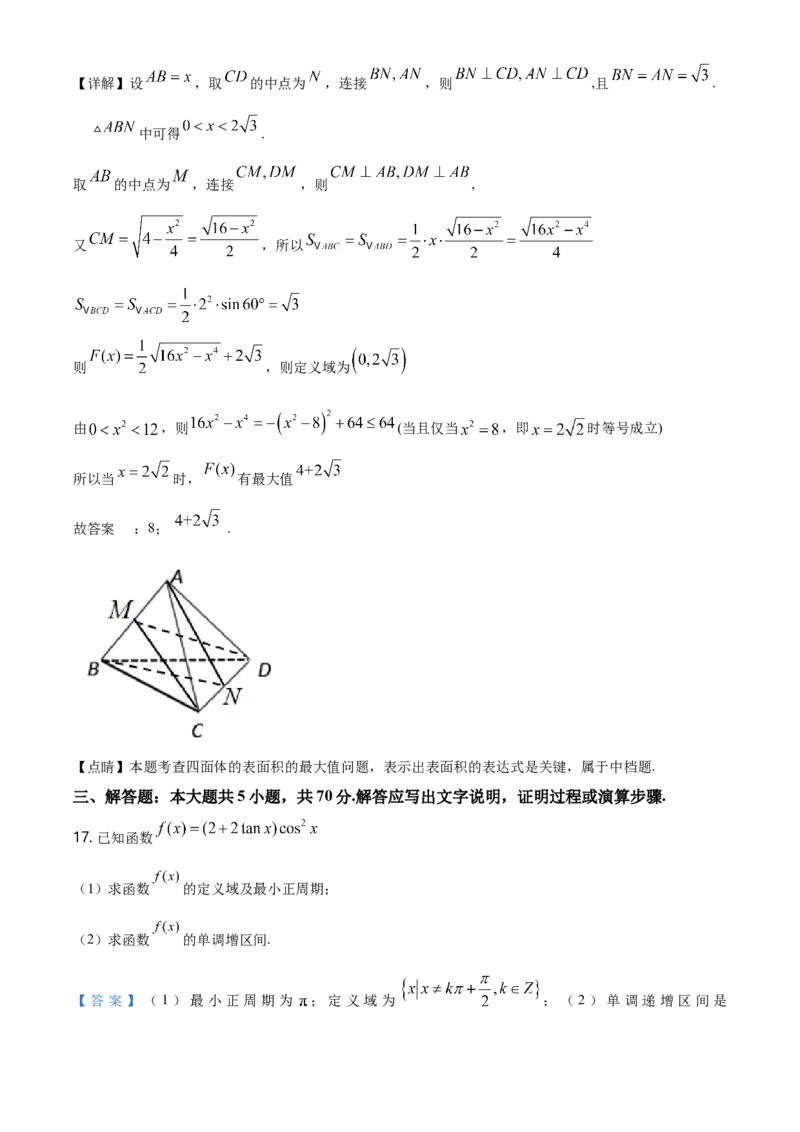
16. 如图,四面体 的一条棱长为 ,其余棱长均为 ,记四面体 的表面积为 ,则函数
的定义域为_______;最大值为_______.
【答案】 (1). (2).
【解析】
【分析】
设 ,取 的中点为 ,连接 ,则 ,且 ,在
中可得 ,取 的中点为 ,连接 ,则 , ,即得到函数的定义
域,由 , ,表示出 ,求出其最大值即可.【详解】设 ,取 的中点为 ,连接 ,则 ,且 .
在中可得 .
取 的中点为 ,连接 ,则 ,
又 ,所以
则 ,则定义域为
由 ,则 (当且仅当 ,即 时等号成立)
.
所以当 时, 有最大值
故答案 为:8; .
【点睛】本题考查四面体的表面积的最大值问题,表示出表面积的表达式是关键,属于中档题.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 已知函数
(1)求函数 的定义域及最小正周期;
(2)求函数 的单调增区间.
【答案】(1)最小正周期为 ;定义域为 ;(2)单调递增区间是.
【解析】
【分析】
(1)将切化弦,并利用二倍角的正弦公式与余弦公式,可得 ,利用周期公式,
可得最小正周期,然后根据正切函数需满足的条件可得函数的定义域.
(2)根据(1)的结论,使用整体法, ,简单计算可得结果.
【详解】(1)因为
所以
所以
所以 的最小正周期为 .
要使 有意义,则 得,
所以 的定义域为
(2)令 得,
,
所以 .所以 单调递增区间是
【点睛】本题考查切弦转化以及辅助角公式,还考查了使用整体法求解正弦型函数的单调区间,掌握基础
的三角函数,熟练使用整体法,化繁为简,考验分析能力以及计算能力,属中档题.
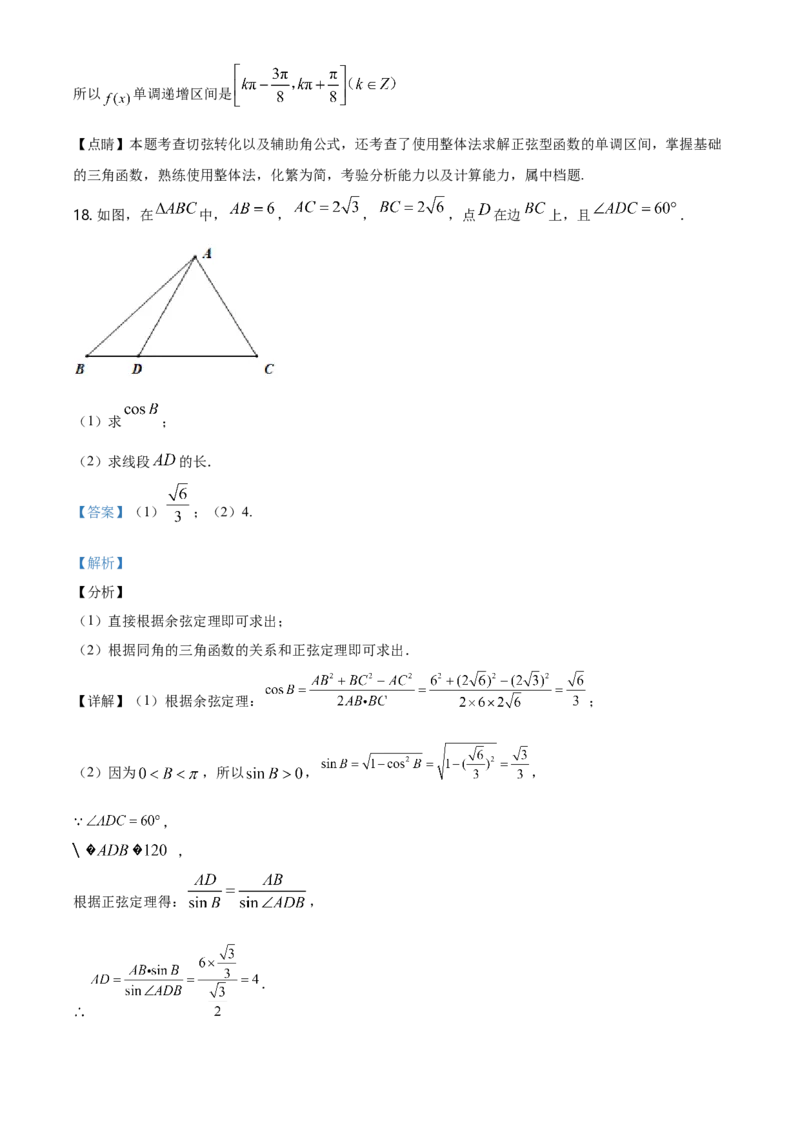
18. 如图,在 中, , , ,点 在边 上,且 .
(1)求 ;
(2)求线段 的长.
【答案】(1) ;(2)4.
【解析】
【分析】
(1)直接根据余弦定理即可求出;
(2)根据同角的三角函数的关系和正弦定理即可求出.
【详解】(1)根据余弦定理: ;
(2)因为 ,所以 , ,
,
,
根据正弦定理得: ,
.【点睛】本题考查利用正余弦定理,同角的三角函数的关系,同时考查了学生的逻辑推理、数学运算等数
学核心素养.属于中档题.
19. 已知函数 满足下列3个条件:
①函数 的周期为 ;② 是函数 的对称轴;③ .
(1)请任选其中二个条件,并求出此时函数 的解析式;
(2)若 ,求函数 的最值.
【答案】(1)答案见解析, ;(2)最大值 ;最小值 .
【解析】
【分析】
(1)由①知 ,由②知 ,由③知 ,结合 即可求
出 的解析式.
(2)由 可得 ,进而可求出函数最值.
【详解】解:(1)选①②,则 ,解得 ,
因为 ,所以 ,即 ;
选①③, ,由 得 ,
因为 ,所以 ,即 ;选②③, ,由 得 ,
因为 ,所以 ,即 .
(2)由题意得,因为 ,所以 .
所以当 即 时, 有最大值 ,
所以当 即 时, 有最小值 .
【点睛】本题考查了三角函数的周期,考查了三角函数的对称轴,考查了三角函数的值域,考查了三角函
数表达式的求解,意在考查学生对于三角函数知识的综合应用.
20. 已知在 中, , , .
(1)求 ;
(2)若 是钝角三角形,求 的面积.
【答案】(1) ;(2) .
【解析】
【分析】
.
(1)利用正弦定理 ,简单计算可得结果
(2)利用余弦定理可得 或 ,然后根据 是钝角三角形以及余弦定理进行验证可确定 ,
最后使用三角形面积公式,可得结果.
【详解】(1)在 中,根据正弦定理得 ,则 ,
所以
(2)因为 ,
所以 .
解得 或 .
当 时,
所以 为钝角,所以△ 的面积
当 时, .
此时 为锐角,不满足题意
所以△ 的面积 .
【点睛】本题考查正弦定理、余弦定理以及面积公式解三角形,重在熟悉公式,考验分析能力以及计算能
力,属基础题.
21. 对于集合 .
.集合 中的元素个数记为 .规定:若集合 满足 ,则
称集合 具有性质 .
(1)已知集合 , ,写出 ,并求出此时 的值;
(2)已知 均有性质 ,且 ,求 的最小值.【答案】(1), , ,
所以 ;(2) .
【解析】
【分析】
(1)根据 的定义求得 ,根据 的定义求得 .
(2)集合 具有性质 ,等价于任意两个元素之和均不相同,则任意两个不同元素之差的绝对值均不相
同,由此构造 并求得 .求得 的表达式,结合绝对值
的性质求得 的最小值.
【详解】(1)由题意知, , ,
所以 .
(2)由题意,集合 具有性质 ,等价于任意两个元素之和均不相同.
如,对于任意的 ,有 ,
等价于 ,即任意两个不同元素之差的绝对值均不相同.
令 ,
由 具有性质 .
因为集合 均有性质 ,且 ,
所以 ,当且仅当 时等号成立.
所以 的最小值为 .【点睛】本小题主要考查新定义集合的理解和应用,属于难题.